光伏不同渗透率下考虑源网荷储深度互动的电力系统调峰策略

杨谦，刘继春，蒋万枭

(四川大学电气工程学院，成都市 610065)

0 引 言

化石能源的枯竭以及环境的恶化，使得以一次能源为核心的传统电力生产消费体系亟待转型。风电、光伏等清洁能源是我国能源领域的重要发展方向，但目前对新能源出力特性维度研究过于单一，并且由于调峰资源及调峰容量的限制，导致系统在高渗透率新能源接入下难以维持系统电力供需平衡，使得系统调峰压力骤增，带来巨大挑战。

对于未来态新能源出力场景的推演已做了大量研究，文献[1]结合实时云图、太阳阴影等对光伏出力的影响，推导出了长时间尺度的光伏场景。文献[2]针对传统预测算法在突变天气条件下预测精度较低的问题，提出基于近邻传播聚类和回声状态网络的组合算法，通过近邻传播算法对光伏出力进行分类，并根据预测日所属类别建立回声网络状态方程进行光伏出力预测。文献[3]利用支持向量机、神经网络及深度学习等机器学习方法对未来态短时间尺度新能源出力场景进行构建。但现有文献大多都仅从新能源某一特性进行建模，并未考虑到新能源出力的多维特性。

电力系统调峰能力是指系统跟随负荷变化的能力，新能源大规模并网后，电力系统调峰能力被严重削弱[4]。在考虑源网荷储的电力系统调峰能力方面的研究，文献[5]建立了考虑峰谷电价的风电-抽水蓄能联合系统和能量转化效益的定量评估模型，研究了风蓄联合系统中抽水蓄能电站对风电移峰填谷的影响；文献[6]建立了可变负荷、储能电池、水电、火电、电制热储热和核电等多种能源以及联络线、频率综合调节模型，进而提出了电网调峰裕度的计算和监测理论。文献[7-8]基于对柔性负荷这一概念的研究和电网调峰调节分析，在传统经济性目标函数的基础上建立了碳交易收益最大和综合发电成本最小的多目标模型，该模型综合考虑了非线性的柔性负荷响应成本和碳排放补偿成本，并增加了柔性负荷约束条件。文献[9]将高载能负荷规划到调峰电源，以增加电力节能水平，从源、网、荷三方面提出电力节能量化指标。文献[10]根据可再生能源系统容量推导适用于光伏和风力发电调峰的存储装置特征参数，通过德国配电网中的发电机实际数据，计算出调峰所需容量和充电循环次数之间的经验关系，确定适当的调峰存储技术。文献[11-12]采用基于调峰充裕性的调峰能力算法，通过计算机组调峰容量来评价系统调峰充裕度，分析京津唐地区在风电并网后系统的调峰能力改变。但以上文献在研究调峰时，均未综合考虑源网荷储各侧资源调峰特性，无法有效促进各侧资源深度互动。

针对上述文献的不足之处，本文提出源网荷储深度互动的电力系统调峰策略。首先，根据光伏不同渗透率，得到在允许峰谷差范围内不同的系统调峰能力需求；然后，刻画源网荷储四侧资源的经济技术特性；最后，利用本文建立的模型得到在源网荷储资源技术特性约束下，与系统调峰能力相匹配的4种资源的最优组合及其投运优先顺序，体现源网荷储资源间互补互济的深度协同能力，完成不同渗透率与系统调峰能力的动态匹配。

1 源网荷储深度互动调峰原理

随着化石能源的枯竭，风电、光伏等新能源发电并网成为必然趋势。其与水力发电、火力发电等常规发电方式最根本的不同点在于其出力具有随机性、间歇性和不可控性。这些特点决定了新能源并网运行时，必须由常规电源为其出力提供补偿，以保证对负荷安全可靠地供电。

目前主流调峰方式是利用电源侧火电机组进行系统调峰，但随着光伏渗透程度逐渐加深，火电机组调峰容量不足且深度调峰经济性较低，这降低了火电机组的调峰积极性，使得系统调峰压力进一步加剧。单一的调峰资源已经不能满足系统调峰需求，因此，迫切需要探究更多类型资源互济支撑方法来平衡系统波动。

不同于传统单一调峰方式，本文提出了源网荷储深度互动的电力系统调峰策略。图1为源网荷储深度互动的调峰原理示意图。

图1 源网荷储深度互动调峰原理Fig.1 Principle of deeply interactive peak regulation of source-network-load-storage

首先，考虑风电出力的波动性、季节性与随机性，收集并补齐风电历史出力数据，通过模糊C均值聚类(fuzzy C-means，FCM)与高斯拟合法得到光伏多维出力特性；然后，刻画了各资源调峰容量、系统故障处理能力、用户满意度等特性，获得不同的调峰策略，也即对应了不同的电力系统调峰能力；最后，以电力系统调峰经济性最优为目标，实现光伏不同渗透率与电力系统调峰能力的最优匹配。

2 源网荷储调峰资源特性分析

2.1 不确定量模型

2.1.1光伏多维特性

光伏发电效率受时间、自然环境以及突发事件等多维度因素影响。光伏发电技术的原理是利用太阳光照射太阳能电池板的光生伏特效应将太阳能转化为电能，其发电量主要受到光照强度、温度等因素影响，因此其出力特性具有随机性、波动性、季节性等特性，同时光照强度、温度等因素大小也将直接影响光伏的出力大小。通过对历史数据进行模糊C均值聚类及高斯拟合，将此类特性模型化，可得光伏出力特性：

(1)

PPV=rηmaxAPVηPVcosθ

(2)

根据统计，一天中太阳辐射量遵循Beta分布，而光伏出力与太阳辐射呈线性关系，故光伏出力也服从Beta分布，如下所示：

(3)

(4)

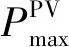
ε1、ε2可由下述公式得到：

(5)

式中：μ、δ分别为某时段内太阳辐射量的均值和标准差。

2.1.2负荷模型

现阶段已有大量文献研究负荷波动，本文采用最为常见的正态分布来描述负荷，如下所示[13]：

(6)

式中：Pload、μL、δL分别为参考时段内负荷值、负荷的均值和标准差。

2.2 源网荷储调峰资源特性分析

现代电力系统调峰资源主要分布在源网荷储四个方面，电源侧通过调节电源出力大小及增设调峰机组来提高系统调峰能力，电网侧通过增加网络弹性来提高系统调峰能力，负荷侧通过负荷分级需求响应来提高调峰能力，储能侧则在电力需求波动高峰时提供/储存额外出力来提高系统调峰能力。

2.2.1常规调峰机组

电源侧主要是增加调峰机组来提高系统调峰能力，常规调峰机组主要有水电和火电机组。水电机组不计调峰成本，故调峰成本主要来自火电。火电机组调峰通常分为基础调峰阶段、不投油深度调峰阶段、投油深度调峰阶段三部分，基础调峰阶段的调峰成本即为燃煤成本和机组的开停机损耗，燃煤量采用耗量特性表示。而投油与不投油深度调峰阶段还需考虑机组的损耗与油耗成本。火电机组深度调峰的成本为[4]：

(7)

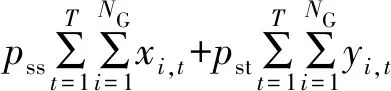
(8)

Csun(PT)=φCunit/[2Nt(PT)]

(9)

Coil=Cconcoil

(10)

式中：PT为火电机组出力；f(PT)为机组耗量特性函数；Csun(PT)、Coil分别为机组损耗成本与机组油耗成本；Pmax为机组最大出力；Pmin为机组基础调峰阶段的最小技术出力；Pa为不投油深度调峰阶段的最低稳燃出力；Pb为投油深度调峰阶段的稳燃极限出力；T、NG分别为总时段数与机组台数；xi,t和yi,t表示机组i在t时段是否切换到启动和停机状态；a、b、c为火电机组煤耗函数系数；Pcoal为当前燃煤价格，元/t；pss、pst分别为机组一次开、停机成本；φ为火电机组运行影响系数，表示不同运行状态对机组的影响；Cunit为机组的购机成本；Nt为转子致裂循环周次，可由转子低周疲劳曲线确定；Ccon为机组运行时的油耗量；coil为当前燃油价格。

由于式(7)为分段函数，不利于求解，因此引入布尔变量m和n，故机组i的调峰成本可改写为：

(11)

(12)

2.2.2输电系统响应

故障应对能力是指电力系统在遇到故障时的紧急处理能力，增强网络弹性可有效降低线路故障概率。电网侧调峰是通过增强电力系统网络弹性来提高电力系统调峰能力，适当改变输电线路的潮流分布可缓解线路过载、节点电压越限等电网阻塞，以增强系统故障应对能力。本文采用的线间潮流控制器(interline power flow controller，IPFC)作为一种功能强大的新型柔性输电系统控制装置，它具备直接控制串联部分所安装线路潮流的能力，而且可以实现不同线路间功率的定向、定量交互，进而达到同时控制不同线路间潮流的目的，IPFC的结构见参考文献[14]。

在确定系统结构参数和负荷的情况下，使用线间潮流控制器改变潮流分布以增强电网弹性，实现系统安全运行的目的。安装IPFC线路增加的有功潮流ΔP、电压差ΔV为：

(13)

(14)

式中：Vi、Vj分别表示节点i和j的电压；Vseij为等效电压源幅值；xij为节点i和j之间的电抗；ψj为Vi与Vj的相位差；Pij表示支路ij的有功功率。

约束条件为：

(15)

分别表示支路ij的有功功率最小、最大值。线间潮流控制器经济成本低，可忽略不计。

2.2.3负荷分级需求响应

图2为负荷分级响应示意图，调度中心可根据智能用电系统确定调峰需求量，上级调度命令逐层到达基层变电站[15-16]，再由负荷中心的数据中心控制多个负荷点按照一定次序响应负荷，实现负荷与电网的需求联动。

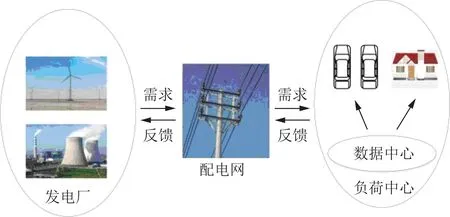
图2 分级需求响应Fig.2 Grading response requirements

由于智能调度中心的存在，本文主要考虑通过可转移负荷实现负荷侧对调峰压力的缓解。可转移负荷是指日常生活中可以变换使用时间的负荷，例如洗衣机、空调等，稍微调整使用时间，对系统产生的影响不大，但会影响用户的满意程度。因此，当需要用户配合进行调峰时，需给用户参与调峰进行补偿。设置不同的用户满意度阈值，使得在根据不同渗透率匹配最优调峰策略时，也可考虑到用户的满意度。可转移费用如下所示：

(16)

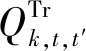
2.2.4储能系统

储能设备通过在负荷低谷时期充电、高峰时期放电来缓解电量缺失和富余情况，进而降低系统负荷峰谷差。储能设备作为电力系统的一种优质调峰资源[17]，可以有效地平滑系统因新能源并网带来的功率波动，合理调度储能设施，鼓励并优先使用储能辅助调峰是解决调峰问题的有效途径。最常见的电池储能系统充放电成本函数如下：

(17)

3 光伏不同渗透率与系统调峰能力匹配

3.1 源网荷储深度互动模型

不同于传统单一资源的调峰方式，源网荷储深度互动调峰方式考虑了各侧资源间互补互济的深度协同能力，再与不同的光伏渗透率匹配出最优策略，以平衡系统峰谷差。针对多因素影响的调峰资源耦合方式建模思路，本文是将一个多因素影响的能源系统抽象成如图3所示的二端口网络。

图3 源网荷储深度互动枢纽Fig.3 Deep interactive hub of source-net-load-storage

图3中f1～fn为该枢纽的输入，包括调峰需求、各侧调峰资源技术特性、用户满意度等；S1～S4为调峰资源类型，其不同的组合方式即代表不同的调峰策略。源网荷储深度互动枢纽输入输出关系可由如下数学模型表示。

(18)

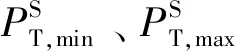
3.2 渗透率与系统调峰能力最优匹配模型

以系统总调峰成本最低为目标函数，得出满足源网荷储资源特性下的最优调峰策略，从而实现光伏渗透率与系统调峰能力的最优匹配。其调峰成本函数如下：

(19)

(20)

(21)

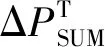
源网荷储多侧资源协同参与调峰时，需满足诸多约束条件，系统电力平衡条件如式(22)所示。

(22)

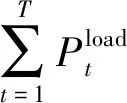
调峰机组约束及系统网络约束条件如(23)—(30)所示。其中，式(23)为调峰机组的出力范围；式(24)—(28)为机组的开停机时间及开停机次数约束。

(23)

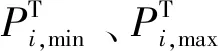
(24)

(25)

(26)

(27)

(28)

BxΦ=P

(29)

(30)

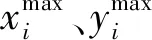
可转移负荷的约束条件如式(31)—(33)所示。

(31)

(32)

(33)

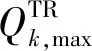
建湖县水稻种植方式主要是麦后直播和机插栽插两种形式，面积大约1：1，水稻品种主要为：淮稻5号、南粳9108、华粳5号、苏秀867、武运粳27等，常年直播稻播种时间在6月10日前后，机插秧在6月20日左右栽插。由于种植方式、栽培品种以及气候条件的变化，其病虫发生表现为三个特点：

储能系统的约束条件如(34)—(37)所示。

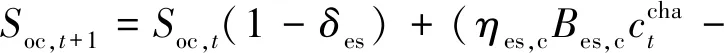
(34)

Soc,min≤Soc,t+1≤Soc,max

(35)

Pes,c,min≤Pcha,t≤Pes,c,max

(36)

Pes,de,min≤Pde,t≤Pes,de,max

(37)

3.3 模型的转化与求解

3.3.1模型的转化

本文建立的优化调度模型是复杂的混合整数二次规划问题，而火电机组深度调峰成本为非线性约束条件，无法利用CPLEX软件求解，故将式(10)、(11)转化为一系列不等式约束集合，即将火电机组深度调峰成本的非线性规划问题转化为混合整数线性规划(mixed integer linear programming，MILP)问题，便于模型利用MATLAB求解。其等效约束如下：

(38)

式中：z代表机组状态变量；g、h分别为大于0的常量，保证m′=z=0,n′=z=0时第4行和第6行不等式成立。

3.3.2匹配模型求解步骤

本文研究光伏不同渗透率与电力系统调峰能力匹配的流程如图4所示。

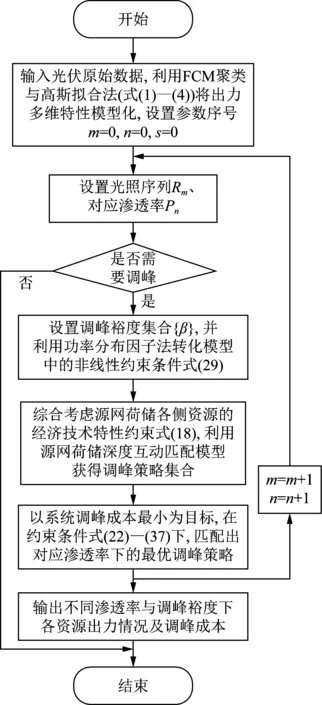
图4 光伏渗透率与调峰能力的匹配流程Fig.4 Matching flowchart of photovoltaic penetration rate and peak regulation capacity

步骤1：收集光伏历史出力数据，利用样条插值法将缺损数据补齐，再利用FCM聚类法与高斯模拟将光伏出力的随机性、波动性等多维特性模型化。

步骤2：设置光照序列 、渗透率序列 、调峰裕度集合。

步骤3：判断系统是否需要调峰，是，则进行下一步。

步骤4：利用功率分布转移因子法将式(29)转化为线性约束条件。

步骤5：综合考虑源网荷储各侧资源的调峰经济技术特性，利用源网荷储深度互动匹配模型获得调峰策略集合。

步骤6：以系统调峰经济性最优为目标，优化出对应光伏渗透率下的最优调峰策略，并调整光伏渗透率、系统调峰裕度。

步骤7：输出不同调峰裕度与不同光伏渗透率下各资源出力及调峰成本。

4 算例分析

4.1 算例系统

本文以改进的某实际电网系统进行仿真分析，网架结构见本文附录图A1。该系统包含2个50 MW的光伏阵列；一座梯级水电站，总装机容量为120 MW。2个容量为10 MW的储能装置，储能设备相关参数见参考文献[18]。其中调峰电厂共有2台机组，忽略机组实际调峰能力，参照我国现有规定，设定Pb为机组额定容量Pn的30%，Pa为Pn的45%，Pmin为Pn的60%。火电机组的参数源于参考文献[19]，如表1所示。其余参数取自于参考文献[20-21]。负荷预测采取本地同年某日的预测值，光伏预测曲线为本地2019年某典型日的光伏阵列的历史出力数据经过FCM拟合而成，如图5所示，改变其装机容量即可对应不同渗透率。本文中煤价选取的是某电厂2019年入炉标煤单价577.55元/t，油价选取的是同年某市12月平均油价6 450.1元/t。

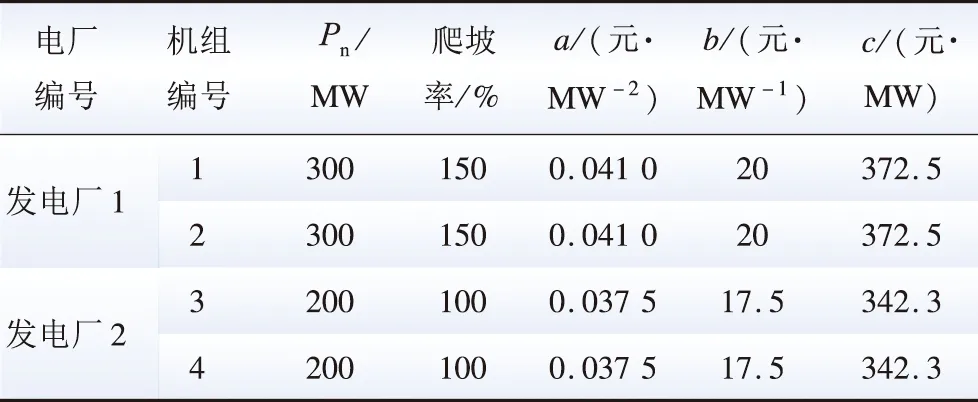
表1 火电机组参数Table 1 Parameters of thermal power units

4.2 源网荷储深度互动分析

选取85%、95%这2种调峰裕度，CON取85，在源网荷储各侧资源深度互动下探究不同渗透率与电力系统调峰能力的最优匹配，得到在10.25%、16.12%、21.71%、28.46%、35.64%这5种渗透率、2种调峰裕度下各调峰资源参与情况，如表2所示。

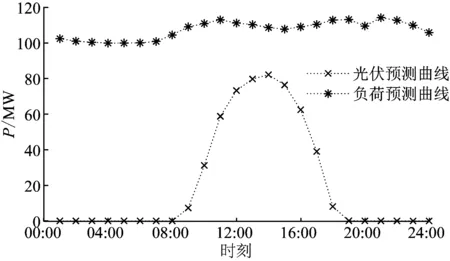
图5 本地负荷与光伏预测曲线Fig.5 Local load and PV forecast curves

由表2中资源组合参与情况可知，储能作为一种优质的调峰资源，调峰成本较小且出力特性稳定，调用优先级高于需求响应。当渗透率较低且为10.25%时，仅由火电机组参与即可完成调峰任务。当渗透率为16.12%时，此时已经产生一定的峰谷差，在85%和95%这2种调峰裕度下，平衡系统波动已需要常规调峰机组与储能设备两者协同完成。当渗透率为21.71%和28.46%时，此时由于储能设备调峰容量有限，系统的波动便需要常规调峰机组、需求响应和储能设备协同完成。而在渗透率为35.64%时，此时光伏渗透率较大，在传输电能时超过了系统的网络约束，则需要线间潮流控制器改变网架中重载线路潮流，在满足线路约束条件后与源荷储三侧资源协同完成系统调峰任务，而传统的利用火电机组调峰方法则可能会出现无法完成调峰任务的情况。由此可见，随着光伏渗透率的升高，系统的波动也越来越大，需要平衡系统波动而参与的调峰资源类型也逐渐增多。

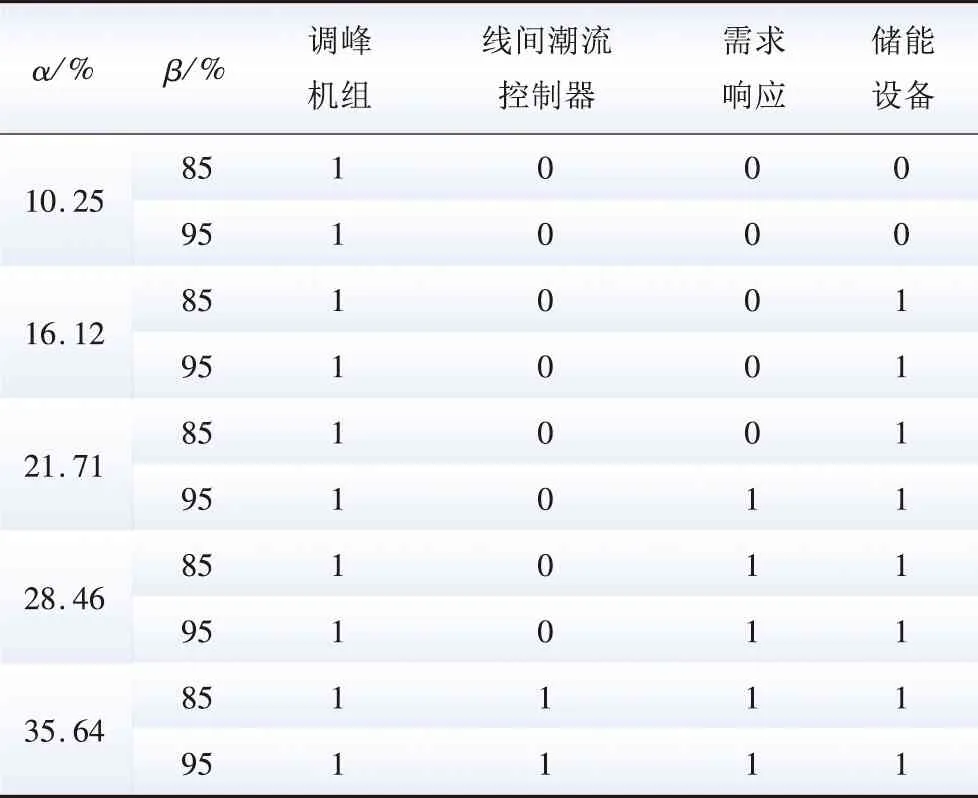
表2 不同渗透率下各资源参与情况Table 2 Resource participation under different penetration rate

4.3 不同渗透率与系统调峰能力的最优策略分析

综合考虑源网荷储四侧调峰资源经济特性，以系统调峰成本最小为目标函数，在经源网荷储四侧资源深度互动匹配出的调峰策略集合中，得出光伏不同渗透率与系统调峰能力的最优匹配策略，得到不同渗透率下各资源的出力情况，如表3所示。

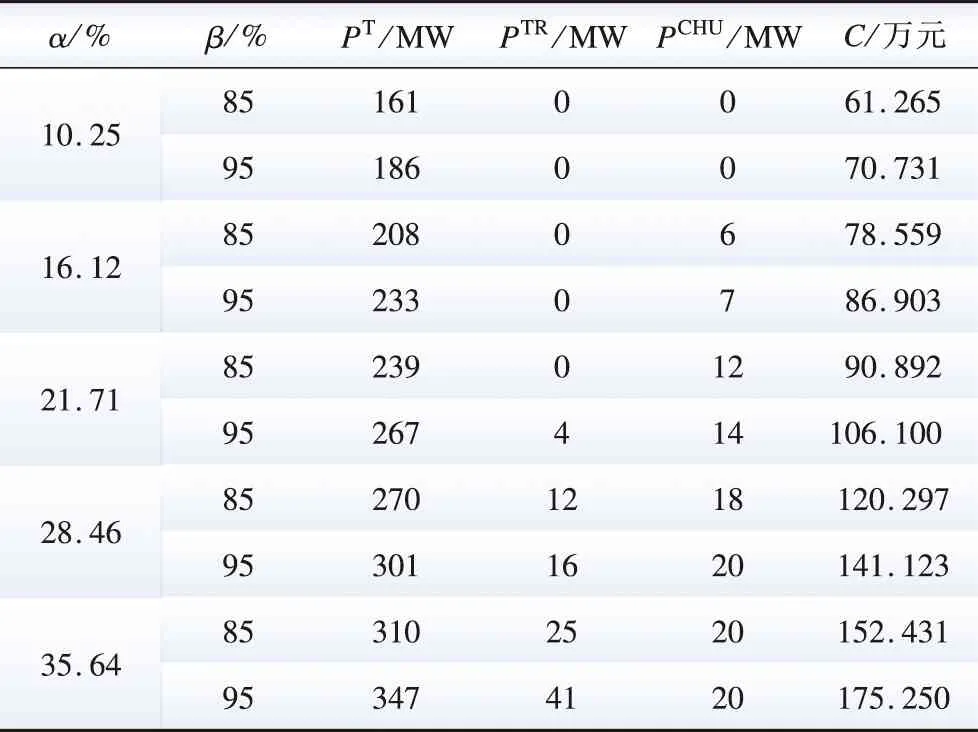
表3 不同渗透率下各资源出力及系统总调峰成本Table 3 Each resource output and system total peak-regulating cost under different penetration rate

由表3可看出，随着渗透率的不断提高，源网荷储参与调峰的资源类型逐渐增加，系统总调峰成本也随之增加。当在渗透率较低时，系统产生的波动仅由火电机组非深度调峰即可完成，此时主要调峰费用包括燃煤成本及火电调峰机组开停机成本。当渗透率在16.12%～21.71%之间时，此时由于光伏出力而产生的部分波动已无法通过火电机组基础调峰阶段进行调节，而储能作为优质的调峰电源，充放电价格与日前市场出清价格关联，而需求侧则会受到用户满意度的影响，故在此阶段也需要一部分的储能调峰成本。当渗透率达到28.46%、调峰裕度为95%时，此时的系统总调峰费用已经高达141.123万元，此时源荷储三侧均已参与到调峰任务中，这是由于储能侧容量有限，且源端调峰机组进入不投油深度调峰阶段，考虑到经济性，则会损失一定的用户满意度增加需求响应成本。当光伏渗透率为35.64%时，此时系统波动导致线路阻塞，则需线间潮流控制器配合源荷储三侧共同工作，改变线路潮流以平衡系统波动。

图6为光伏不同渗透率下、调峰裕度取85%与95%时，传统的单一资源火电机组调峰与本文提出的源网荷储深度互动调峰策略的系统调峰成本对比。从图中可看出，当渗透率为10.25%与16.12%时，两种方法的调峰成本基本相同，这是因为在低渗透率下，系统的波动大多都由火电机组平衡，此时的调峰成本都为机组煤耗成本与机组开停机成本。当渗透率大于21.71%时，参与系统调峰的资源类型逐渐增多，而并不局限于传统的利用火电机组深度调峰完成，减少了油耗及损耗成本，因此，源网荷储深度互动调峰方法成本逐渐低于传统调峰方法的成本。

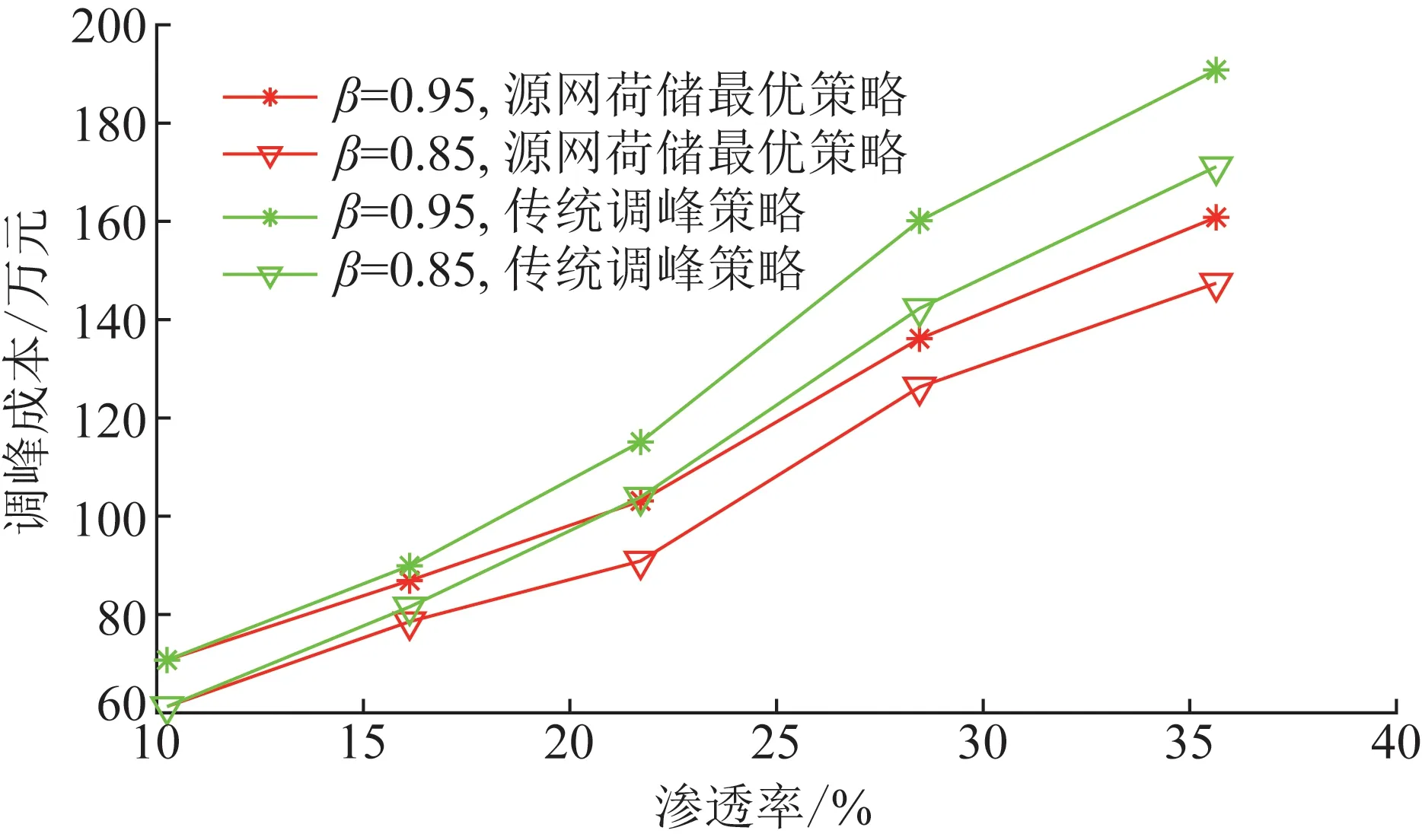
图6 传统调峰与源网荷储最优策略成本比较Fig.6 Cost comparison between the traditional method and the optimal strategy of source-network-load-storage

图7为在源网荷储各侧资源深度互动后，不同光伏渗透率及调峰裕度条件下各资源的调峰成本。

由图7可知，在不同渗透率下，源端火电机组调峰成本远大于其他两种调峰资源的成本，这是由于火电机组的调峰容量远大于储能和负荷侧资源的调峰容量。随着光伏渗透率的升高，光伏出力波动性变大，一部分火电机组逐渐进入深度调峰阶段，油耗及损耗也大大增加，火电机组调峰成本也随之变大，因此需要采取增加调峰补偿等手段来刺激火电机组的调峰积极性。与此同时，当α≤10.25%时，调峰成本仅为火电机组常规调峰成本，此时光伏渗透率较低，仅调用火电机组进行基础调峰即可完成；当10.25%<α≤21.71%时，此时净负荷波动变大，由于储能经济性较高且不会影响负荷满意度，调用源储两侧资源可完成调峰任务；当21.71%<α<28.46%时，此时高渗透率下峰谷差波动更大，为保证经济性，故源荷储三侧资源均参与了系统调峰任务；而当α≥35.64%时，此时易造成网络阻塞，可调用IPFC适当改变线路潮流，四侧资源协同完成调峰任务。可以看出，各资源参与调峰的优先级均是以系统调峰经济性最优为目标来确定，这与本文所建立优化模型的逻辑是相符的。

图8为不同光伏渗透率下火电调峰机组各种损耗的成本曲线，图8(a)为传统单一的火电机组调峰方式，图8(b)为本文提出的源网荷储深度互动调峰方式。从图8两图对比可以发现，两种调峰策略下的机组开停机成本并没有太大变化，油耗与机组损耗则发生了较大变化。这是由于火电机组的开停机成本较高，当渗透率较高时，火电机组可进入不投油深度调峰阶段、投油深度调峰阶段，减少机组的开停机次数。同时，由于调峰资源容量增多，在不同渗透率下源网荷储深度互动方式的经济性则更优。

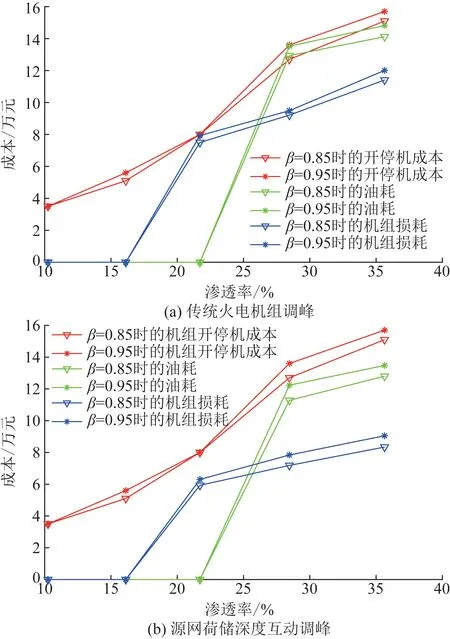
图8 不同光伏渗透率下调峰机组损耗成本Fig.8 Loss cost of peak-regulating units under different penetration rate

图9为不同光伏渗透率区间源网荷储深度互动调峰策略中调峰资源的组合情况。随着光伏渗透率逐渐升高，根据经济性目标求得的最优调峰策略中资源的种类也越来越多。可见，随着光伏渗透率的升高，系统的调峰容量需求也逐渐增大。

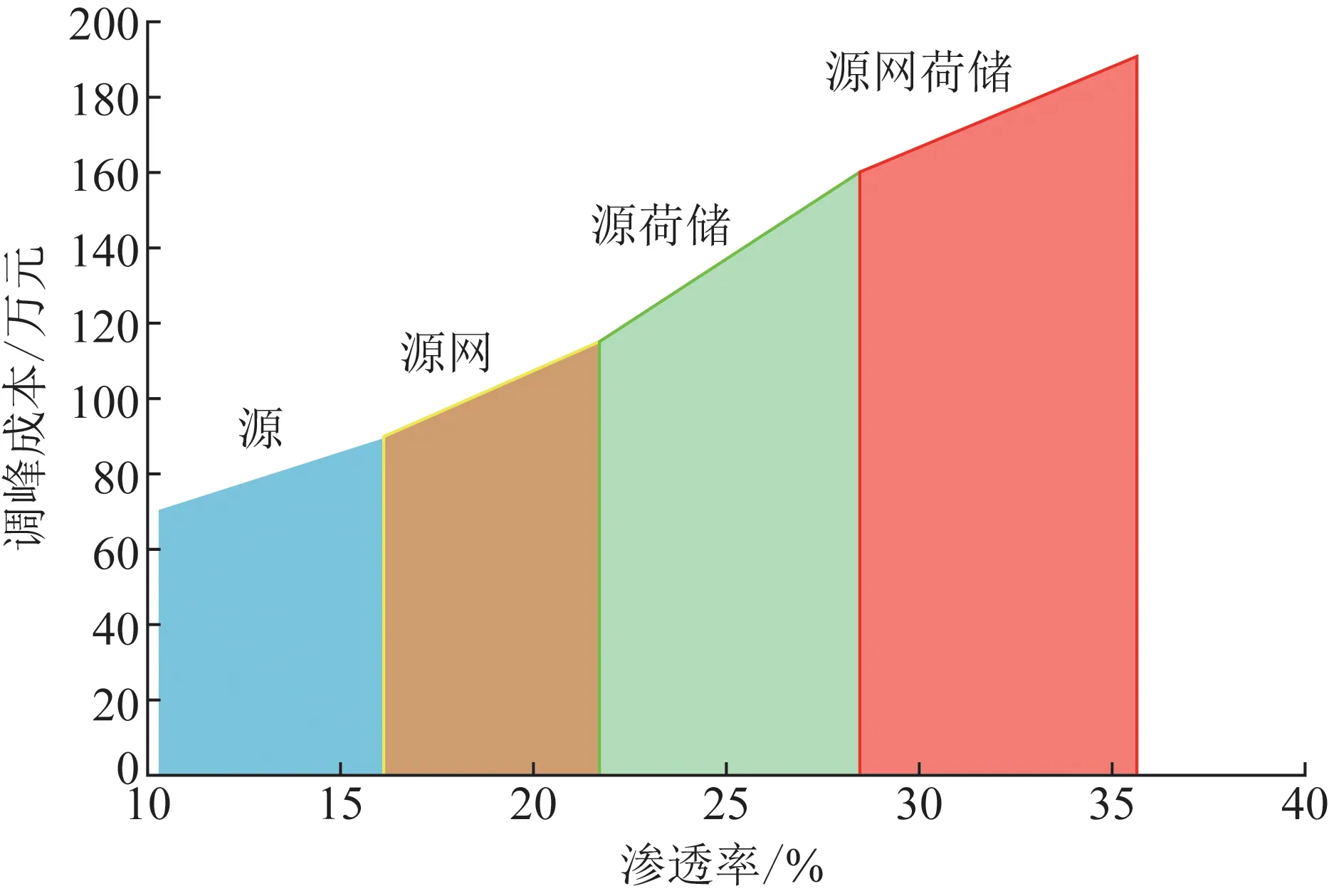
图9 不同光伏渗透率下的调峰策略Fig.9 Peak regulation strategies under different penetration rate

5 结 论

本文基于光伏大规模并网的背景，综合分析了源网荷储四侧调峰资源间的互补互济能力，利用源网荷储深度互动实现了不同光伏渗透率与系统调峰能力的匹配。本文研究表明：

1)随着光伏渗透率的增大，系统的调峰压力也随之升高，通过源网荷储深度互动，能够充分利用调峰资源减小系统调峰压力，提高系统供电可靠性。

2)在不同的光伏渗透率下设置系统调峰裕度，根据源网荷储各侧资源调峰特性得出对应光伏渗透率下的最优调峰策略，实现光伏渗透率与电力系统调峰能力的匹配。

3)在不同渗透率与调峰裕度下，调峰容量的增加减缓了火电机组进入深度调峰的时段，系统及火电机组调峰成本对应减少。故伴随新能源并网规模变大，可适当增加系统调峰容量提高系统调峰能力。

本文提出的源网荷储深度互动调峰策略，可在未来新能源大规模并网下为解决因新能源多维时空特性而造成的系统调峰需求问题提供参考，对提高和稳定系统调峰需求具有重要意义。在电力市场环境下，基于市场资源配置与系统调峰能力匹配从而提高新能源消纳将是下一步研究方向。