换流站交流出线方式对换流变空投的影响

王彤彤，文俊，靳海强，韩民晓

(华北电力大学电气与电子工程学院，北京市 102206)

0 引 言

变压器空投是指二次绕组开路时，一次绕组接入电网的过程，故又称为空载合闸或空充[1]。新建或检修后的直流工程投运时，首先应进行换流变的空投，属于换流站的常规操作。换流变空投过程中，可能伴随励磁涌流和铁磁谐振现象。正常运行时，换流变的励磁电流一般不超过其额定电流的2%，但是空投时，励磁电流会增大到额定励磁电流的6～8倍，故称为励磁涌流[2-4]。励磁涌流可能导致换流变无法正常投入、差动保护误动作等严重后果。励磁涌流的主要成分为2、3、4、5 等低次谐波，以2次谐波为主，通常谐波电流总畸变率可达28%以上[5-7]。例如，2007年天广直流工程调试期间，换流变空投使3次谐波电流迅速增加，导致运行中的3/36(B型)交流滤波器的避雷器炸裂。与普通电力变压器相比，换流变电压高、容量大，漏抗很大，因此换流变空投引发的励磁涌流更大，谐波含量更严重[8-10]。其次，空投时，变压器绕组电感降低，从而与线路电容或先期投入的交流滤波器及无功补偿设备发生铁磁谐振，产生过电压，威胁换流变及运行检修人员的安全[11-13]。过电压、过电流的严重程度与交流系统短路容量、合闸断路器是否带合闸电阻及换流站中其他设备的种类及布置方式等有关。

迄今为止，我国所有换流站均通过交流架空线路接入交流输电网。电缆线路由于供电可靠性高，运行维护费用较低而广泛应用于城市配电网中[14-16]。大量新工艺的运用明显改善了电缆线路的各项性能指标，促使高压、超高压电缆线路逐渐应用于输电网中。如2010年4月，随着我国首座超大容量、多电压等级、全地下、全数字变电站——静安变电站的投运，我国第一回500 kV超高压长距离用于城市电网的三林—静安电缆线路投入运行。之后，虹杨—杨行500 kV电缆线路投运，北京、广州等大城市也相继敷设了500 kV电缆线路，电缆线路已成为未来城市输电网建设的发展趋势。

随着输电网中电缆线路占比的增加，电缆线路电抗小、对地电容大的特点势必改变换流站与输电网间的谐振特性。因此，提前开展电缆线路出线方式及交流系统中电缆线路占比的研究很有必要，可为今后换流变保护配置、换流站绝缘配合等直流工程设计提供理论基础。

本文首先分析换流变空投的两类典型现象：励磁涌流和铁磁谐振，深刻揭示它们产生过电流、过电压的机理。然后，以我国典型的±500 kV直流工程的换流变为例，分别建立换流站2种交流出线方式——架空线路出线、电缆线路出线，同时计及交流系统中电缆线路占比的换流变空投电路模型。最后仿真研究换流站不同出线方式、电缆线路占比及断路器合闸电阻对励磁涌流和铁磁谐振的影响，给出换流站抑制过电流和过电压的建议。

1 换流变空投引发的问题

1.1 换流变空投过程

直流工程既可双极运行也可单极运行，运行中的换流站不仅包含换流变、交流滤波器和无功补偿装置等交流设备，同时还包含12脉动换流器、直流滤波器等直流设备[8]。当正常起动单极直流时，换流变空投示意图如图1所示。图1中，换流母线b经交流出线l接入交流输电网，同时通过合闸断路器(S1、S2)与换流变(T1、T2)相连。换流变空投过程中，直流系统尚未投运，因此接于换流母线上的交流滤波器和无功补偿装置未投入，故图1中未画出。每组换流变通常由3台单相双绕组变压器组成，分别采用YNy0和YNd11(或YNd1)连接组别，向6脉动换流器提供交流电压。

换流变空投为直流工程正常起动的第一步。换流变空投过程为：当12脉动换流器处于闭锁状态且换流变充电条件具备后，同时闭合S1、S2，即对换流变和12脉动换流器充电。由于12脉动换流器尚未解锁，所以不工作，对应于换流变二次绕组开路。换流变空投时，换流变瞬时并入电压很高的输电网，使换流变铁芯急速饱和，可能产生换流变空投的2类典型现象：励磁涌流和铁磁谐振。以下分别分析2种现象的产生机理。

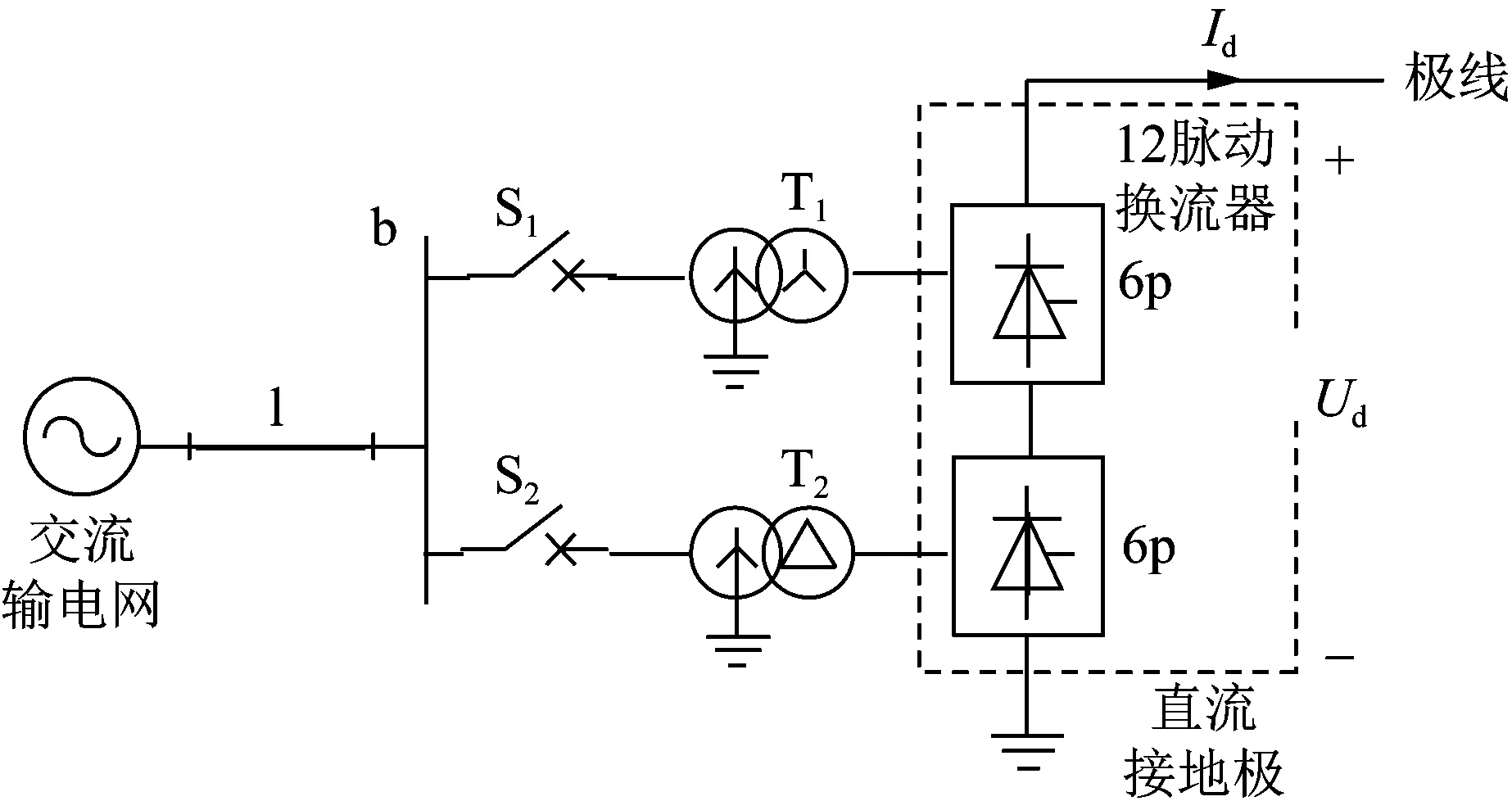
图1 单极直流换流变空投示意图Fig.1 Schematic diagram of no-load transformer closing of single-pole DC converter

1.2 励磁涌流

以单相双绕组换流变为例分析空投时励磁涌流的产生机理。断路器空载合闸瞬间，换流变一次绕组接入换流母线，流过空载电流。空载电流产生空载磁势，并建立交变磁通。由于铁芯的磁导率比油或空气大得多，因此，绝大部分磁力线通过铁芯闭合，该部分磁力线同时匝链一次、二次绕组，相应的磁通称为主磁通。另有少量磁力线通过换流变内部的油或空气闭合，这部分磁力线仅与一次绕组匝链，对应的磁通称为一次绕组漏磁通。空载电流i0流经的路径如图2所示，Rs、Ls分别为换流变交流出线的线路电阻、线路电感，R1、L1分别为换流变一次绕组的漏电阻、漏电感，Rm、Lm分别为换流变的励磁电阻、励磁电感。

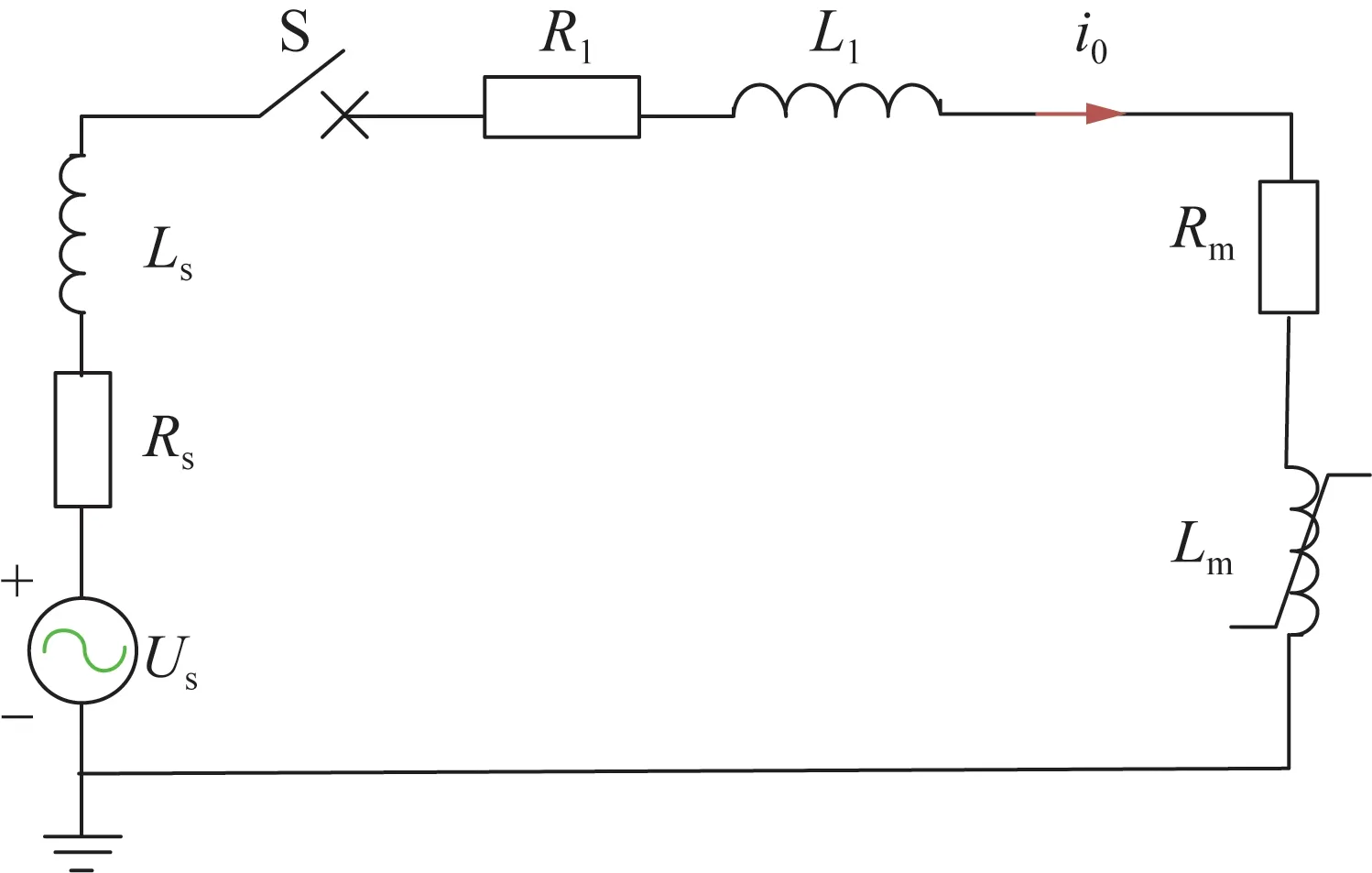
图2 换流变空投时的等值电路Fig.2 Equivalent circuit of no-load closing of the converter transformer

设开关S于t=t0时合闸，由基尔霍夫电压定律得一次绕组电压方程为：

(1)

式中：Usm、θ分别为S合闸时换流母线电压us的幅值和初相角(亦称合闸角)，其中θ=ωt，ω为电网额定角频率；R=R1+Rm+Rs为换流变空投电路的等效电阻；N为一次绕组匝数；φ为总磁通，包含主磁通和一次绕组漏磁通。

电阻R1、Rm分别反映一次绕组的铜耗和铁芯的铁耗(含磁滞及涡流损耗)水平，加之合闸初始阶段的空载电流i0非常小，因此电阻压降Ri0很小，可忽略不计。此时，解微分方程(1)得铁芯中的总磁通为：

φ=-φmcos(ωt+θ)+(φmcosθ+φr)e(-t/τ)

(2)

式中：第1项为电压强制产生的稳态磁通分量，幅值φm=Usm/Nω；第2项为维持合闸时刻磁通连续而产生的暂态磁通(又称自由磁通)分量，这是一个按指数规律衰减的非周期分量，衰减时间常数为τ=L/R,其中：L=L1+Lm+Ls，为换流变空投电路的等效电感，φr为剩磁。

式(2)表明，合闸时磁通的数值与换流母线电压us的初相角和剩磁有关。当φmcosθ+φr=0，即θ=arccos(-φr/φm)时，磁场的建立没有瞬变过程而立刻进入稳态，即一合闸就建立了稳态磁通。特别的，如果不计剩磁，此状态对应初相角θ=90°

由于衰减时间常数大，暂态磁通衰减缓慢。考虑最不利的情况：不计衰减且φr与非周期分量磁通φmcosθ方向相同，则总磁通φ由φr开始变化，经过约半个工频周期后，达到最大值φmax=2φm+φr，如图3所示。

图3 合闸后的磁通波形(不计暂态磁通衰减)Fig.3 Flux waveform after closing (excluding transient magnetic flux attenuation)

换流变铁芯具有非线性的磁化特性[7]，如图4所示，线段ab、bc及c点之后分别为近似线性段、饱和段和深度饱和段。对于ab段，空载电流i0小，主磁通φ随i0近似线性增加；进入饱和段后随着i0增加，φ上升缓慢直至不变。

图4 换流变铁芯磁化特性曲线Fig.4 magnetization curve of Converter transformer core

为降低损耗，提高铁芯材料的利用率，换流变通常设计工作在接近饱和段的线性段。由图4可见，正常运行时换流变的励磁电感很大，其阻抗电压μk通常为16%～18%，特高压直流工程的换流变，其μk高达20%左右，远高于其他电力变压器。空投时，换流变铁芯中的磁通由较小的剩磁急剧增大，在最不利时，最大磁通将超过2倍稳态磁通幅值，促使铁芯磁通瞬间饱和，变压器绕组电感快速降低，故合闸电流增加的倍数远远超过磁通增加的倍数，形成数值很大的励磁涌流。换流变的空载电流最大值可达额定励磁电流的6～8倍，之后空载电流将按指数规律减小。一般小型变压器衰减快，约几个周期即达稳定状态。对于换流变等大型变压器，衰减较慢，甚至延续到20 s左右。

综上所述，影响励磁涌流大小的因素主要有以下3种：

1)电源电压。电源电压越高，电压强制产生的稳态磁通幅值越大，励磁涌流越大；

2)合闸角。合闸角越接近0°，铁芯磁通饱和越严重，励磁涌流越大；合闸角越接近90°，励磁涌流越小，甚至可能不出现暂态励磁电流；

3)剩磁。剩磁的方向与合闸后φmcosθ同向时，剩磁越大，励磁涌流越大；反之，剩磁的方向与合闸后φmcosθ反向时，剩磁越小，则励磁涌流越小。此外，励磁涌流还与衰减时间常数、合闸电路阻抗以及变压器容量等因素有关。

变压器的非线性励磁特性可能产生很大的励磁涌流，其中主要为以3次谐波为主的奇次谐波。由于励磁电感随着励磁电流的变化在饱和与不饱和之间作周期性变化，其变化频率是工频的2倍，只有当励磁电感在饱和阶段时，才会出现励磁涌流，因此励磁涌流是断续的，其中主要为以2次谐波为主的偶次谐波及直流分量。综上所述，励磁电流中主要包含2、3、4、5等低次谐波。

1.3 并联铁磁谐振

为便于研究铁磁谐振，将图1所示系统进行等效，由换流母线看向电网的电路呈现容性，假设为 RC并联电路，则换流变空投引起并联铁磁谐振的简化电路如图5(a)所示。图中，Is为交流系统等效电流源，R为交流系统等效电阻，C主要为换流站交流出线的对地耦合电容。由于换流变一次绕组漏磁通仅占主磁通的1/1 000左右，故可忽略不计一次绕组漏电感，只考虑励磁电感Lm，同时不计换流变的电阻。

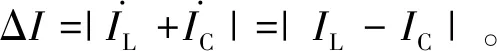
图5 并联铁磁谐振说明Fig.5 Parallel ferromagnetic resonance

为简要阐明并联铁磁谐振产生机理，图5(b)中未计及电阻R，曲线ΔI与电源电流Is相交于a1、a2和a33个点，其中，a1、a3为稳定平衡点，a2为不稳定平衡点。以a1为例，如果系统扰动导致电压增加，IL和IC均增大，而IL增加更多，因此ΔI增加，此时Is低于上升后的ΔI，电压无法维持，于是电压下降，最终恢复至a1点。对于a2点而言，电压扰动而有所增大时，IL和IC均增加，但IC增加更多，因此ΔI减小。由于Is>ΔI，致使电压继续上升，最后只能稳定至a3点。

如果外加电压从0开始逐渐增大，换流变将稳定运行于a1点，此时铁芯处在磁化特性曲线的线性段，电压、电流均很小，不会出现铁磁谐振。换流变空投时，铁芯磁通急剧增大，瞬间饱和，变压器绕组电感迅速降低。工作点迅速越过a1到达a2点，但a2点为非稳定平衡点，故将继续随着Lm的进一步减小而到达并联谐振点Q。此时Lm与电容C形成并联谐振，换流变产生过电压。如果系统等效电阻小，则并联谐振激发后可以自保持，此时称系统发生了并联铁磁谐振。此谐振的本质是铁芯磁通饱和使励磁电感非线性减小，故又称为非线性谐振。

按照谐振频率划分，变压器的铁磁谐振分为三类：谐振频率等于工频的工频谐振，也称基波谐振；谐振频率为工频整数倍的高频谐振，也称高次谐波谐振；谐振频率为工频分数倍的分频谐振，也称间谐波谐振。

综上所述，换流变空投时与电网发生并联铁磁谐振的充要条件是：

1)并网点具有足够大的对地容性设备，如交流输电线路的对地耦合电容、交流滤波器及无功补偿设备；

2)换流变励磁电感具有非线性特性，且换流变与电容设备的伏安特性曲线有交点；

3)换流母线电压足够高，使铁芯迅速饱和，从而使感抗低于容抗；

4)谐振回路的电阻足够小，使谐振激发后维持较长时间不衰减。

2 仿真系统建模

本文基于 PSCAD/EMTDC仿真软件对典型直流工程的单极直流换流变空投系统(如图1所示)进行仿真建模，该典型直流工程参数为±500 kV、3 000 MW，接入500 kV交流输电网。

2.1 电网模型

采用戴维南等值电路对交流输电网进行等效。已知换流母线处的电网额定电压、最大短路电流及最小短路电流分别为535 kV、63.0 kA、23.7 kA，计算得到电网等值阻抗为4.903～13.033 Ω。

2.2 换流站出线方式及交流出线模型

计及电缆线路不同占比对换流变空投的影响，本文设定以下2种换流站出线方式：

1)M1方式：先经架空线路再由电缆线路接入电网；

2)M2方式：先经电缆线路再由架空线路接入电网。

无论何种出线方式，设换流站出线线路总长l为100 km，其中电缆线路长lC，电缆线路占比为σ=lC/l。

架空线路和电缆线路均采用π型等值电路。对于长度为lX的换流站交流出线，用等效阻抗Z及导纳Y表征的线路集中参数模型为：

(3)

式中:r0、x0、g0、b0分别表示单位长度交流线路的电阻、电抗、电导和电纳。由于交流线路的泄漏电流很小，所以g0通常忽略不计。

本文选用的500 kV换流站典型交流出线的参数为[16]：

1)架空线路：r0=0.016 Ω/km，x0=0.263 Ω/km，b0=1.76×10-6S/km；

2)电缆线路：r0=0.058 Ω/km，x0=0.192 Ω/km，b0=62.14×10-6S/km。

2.3 换流变模型

换流变采用基于UMEC(unified magnetic equivalent circuit)理论的铁芯饱和模型，参数见表1，其空载励磁特性曲线如图6所示。对图6所示的换流变空载励磁特性曲线采用完全插值法，利用分段线性化的励磁特性曲线近似表征变压器铁芯的饱和特性。

表1 换流变基本参数Table 1 Basic parameters of converter transformer

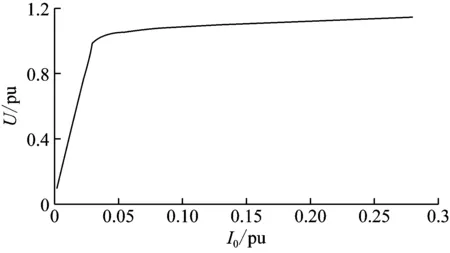
图6 换流变空载励磁特性曲线Fig.6 Excitation characteristic curve of converter transformer

3 换流变空投的影响分析

基于以上PSCAD/EMTDC仿真模型，对上述2种换流站出线方式和不同电缆线路占比进行励磁涌流和铁磁谐振的仿真分析。鉴于励磁涌流导致换流变保护误动的情况时有发生，因此合闸断路器通常安装了并联合闸电阻，在断路器合闸或重合闸过程中，在主触头闭合前短时投入合闸电阻Rs，以抑制励磁涌流和暂态过电压。本文取Rs=1 500 Ω，分别对是否投入合闸电阻进行仿真。设合闸断路器于0.5 s时闭合，启动换流变空投。

3.1 励磁涌流影响分析

由于合闸角对励磁涌流的影响很大，本文考虑最不利的条件，取合闸角为0°，即换流变在换流母线电压过零时合闸。分别对以下2种换流站交流出线方式进行仿真：1)全部采用架空线路，即M1出线方式且电缆线路占比σ=0，用M1(σ=0)表示；2)全部采用电缆线路，即M2出线方式且σ=1，用M2(σ=1)表示。仿真结果如表2所示，三相励磁涌流峰值I0Am、I0Bm、I0Cm为合闸半个周期时的三相电流值，三相励磁涌流衰减时间t0A、t0B、t0C为励磁涌流衰减到1pu且保持在±2%范围内的时间，βHRI0A为a相励磁涌流中2～5次谐波含有率。M1(σ=0)方式且不计断路器合闸电阻时的三相励磁涌流仿真波形见图7，图中同时展示了空投70 ms内的励磁涌流波形局部放大图。

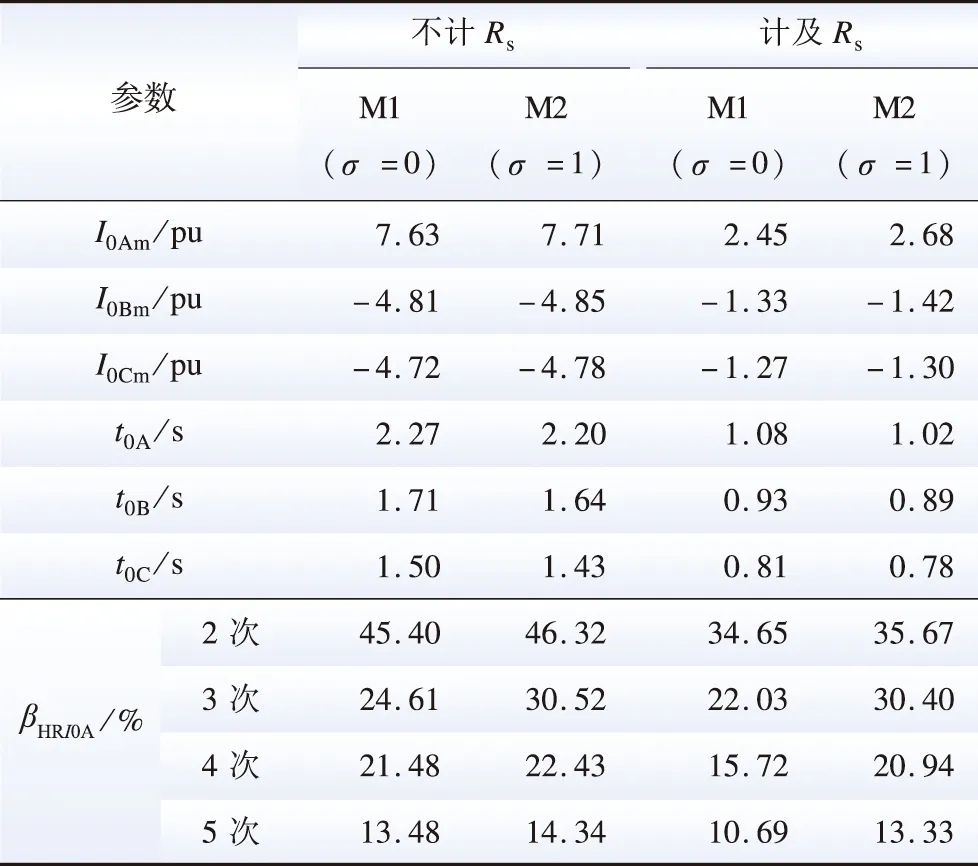
表2 励磁涌流仿真结果Table 2 Results of inrush current

表2及图7揭示了励磁涌流具有如下特点。

1)断续性：每个周期同时包含电流非零和持续为零2个阶段。一般将电流为零的时段用电角度表示，称为“间断角”，约为 200°，对应铁芯的非饱和阶段；其余时段铁芯饱和，出现励磁涌流，约为160°。随着时间的增加，间断角逐渐增大，最终接近360°，而励磁涌流的持续时段逐渐减小，最终接近0°。

2)偏向性：电流波形偏向时间轴的一侧，这是由铁芯磁通的非周期分量导致的。偏向正侧或负侧，则由剩磁的极性、数值以及合闸角三者共同决定。特别地，当满足φmcosθ+φr=0时，磁场的建立没有瞬变过程而立刻进入稳态，因此不会产生励磁涌流，但是其余两相仍然可能出现励磁涌流。

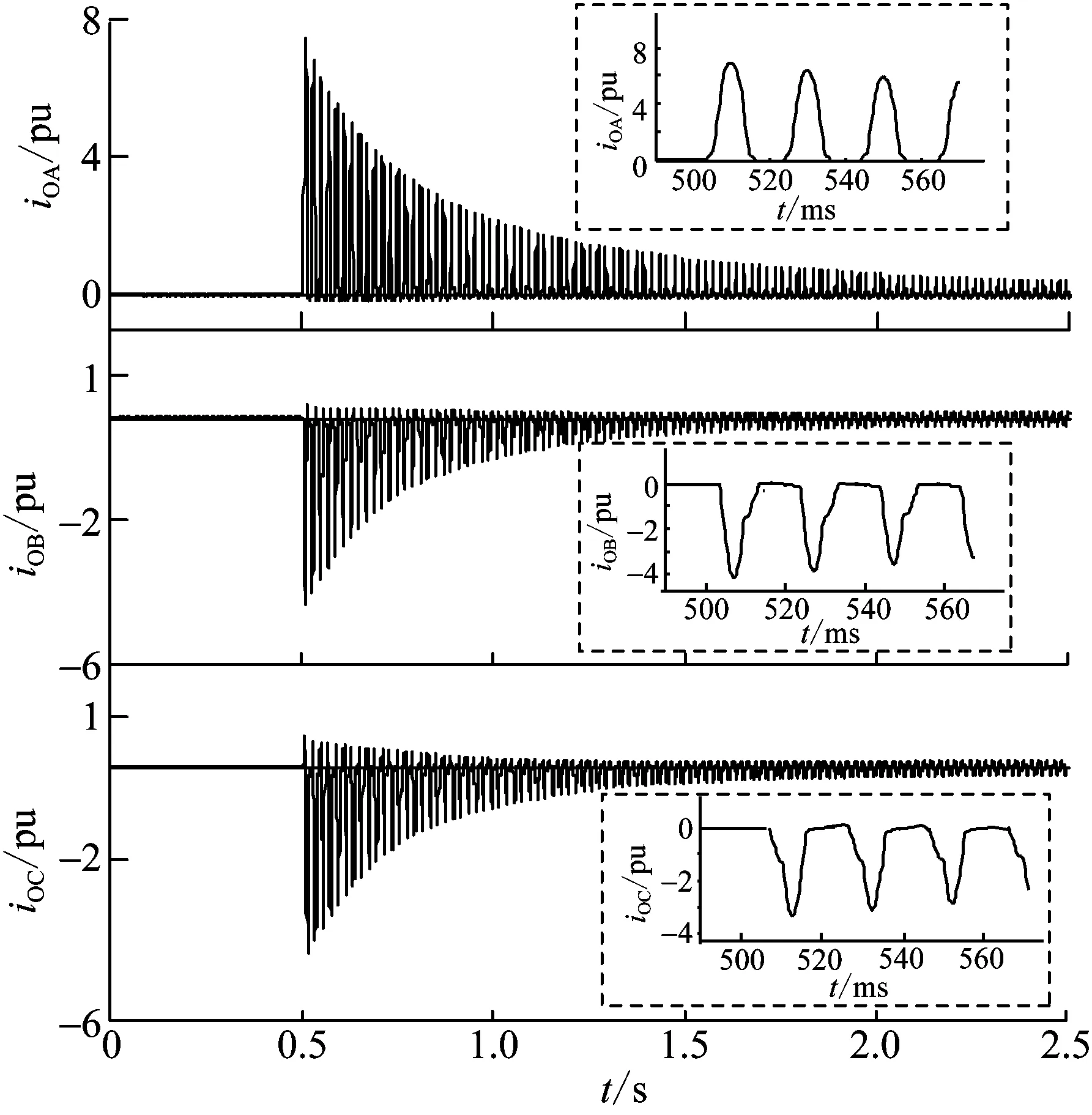
图7 M1(σ=0)且不计Rs时的励磁涌流波形Fig.7 Inrush current waveform excluding Rs at M1(σ=0)

3)非对称性：正负半周期波形不再镜像对称，半周期波形也不再左右对称。前者是因为磁通在每半个周期内的饱和程度不同，后者由非周期分量磁通引起。

4)谐波特性：励磁涌流波形畸变严重，因此谐波严重，其中2、3、4、5次谐波含有率较大。以架空出线且不计合闸电阻为例，a相励磁涌流中2、3、4、5次谐波的谐波含有率分别达到45.40%、24.61%、21.48%、13.48%。

5)三相励磁涌流峰值及衰减时间各不相同：以架空线路出线且不计合闸电阻为例，a、b、c三相的励磁涌流峰值分别为7.63、-4.81、-4.72 pu，三相衰减时间分别为2.27、1.71、1.50 s。三相励磁涌流峰值最大相差约40%，因为a相取为最严重的0°合闸角，其余两相的最大磁通约减少一半，对应的励磁涌流峰值也将减少约一半，由于三相电路的衰减时间常数基本相同，因此励磁涌流峰值的大小直接决定了衰减时间的长短。

6)合闸电阻的影响：无论交流架空出线还是电缆出线，合闸电阻Rs都能有效抑制励磁涌流，这是因为Rs极大的提高了合闸回路的阻尼作用，加快了非周期励磁电流的衰减。

7)电缆出线方式的影响：架空线路出线方式改为电缆线路出线方式对励磁涌流的影响微弱。具体表现为电缆出线方式下的励磁涌流峰值略有增加，最大增幅分别为1.27%(不计Rs)、9.37%(计及Rs)；衰减时间略有降低，最大减幅分别为2.00%(不计Rs)、2.94%(计及Rs)。表明换流站交流出线方式对励磁涌流的影响可以忽略不计。

综上所述，抑制换流变励磁涌流的有效措施有：1)投入合闸电阻；2)避免合闸角为0°；3)换流变去磁，即减小剩磁。

3.2 铁磁谐振影响分析

3.2.1 出线方式及电缆线路占比对铁磁谐振影响

以M2(σ=0.8)方式为例，换流变于t1=0.5 s时空投，a相换流母线电压及空载电流仿真结果如图8(a)所示。可见，换流变经过t1～t2时段的不稳定谐振，于t2=1.0 s进入稳定的铁磁谐振状态，虚线内的局部放大图见图8(b)。此时的最大电压峰值和空载电流峰值分别为额定值的2.71倍和1.23倍，处于过电压状态。铁磁谐振频率为50 Hz，属于工频谐振。而在不稳定谐振期间，过电压更严重，并出现了过电流，最大电压峰值和空载电流峰值分别为4.63 pu和1.81 pu。由此说明，换流变空投导致的铁磁谐振无论处于稳定或不稳定谐振状态，均会产生过电压，甚至会出现过电流，不利于换流变的安全运行。

图8 M2(σ=0.8)铁磁谐振电压电流波形(无合闸电阻)Fig.8 Voltage and current waveform during ferromagnetic resonance without closing resistance at M2 (σ =0.8)

使电缆线路占比σ在0～1.0范围内变化，针对换流站2类出线方式(M1、M2)的仿真结果如表3所示。由于σ=0～0.5内没有发生铁磁谐振，故表中未予列出。表中，UAm、IAm、fr分别为铁磁谐振期间a相的换流母线电压峰值、空载电流峰值及铁磁谐振频率，“—”表示未发生铁磁谐振。

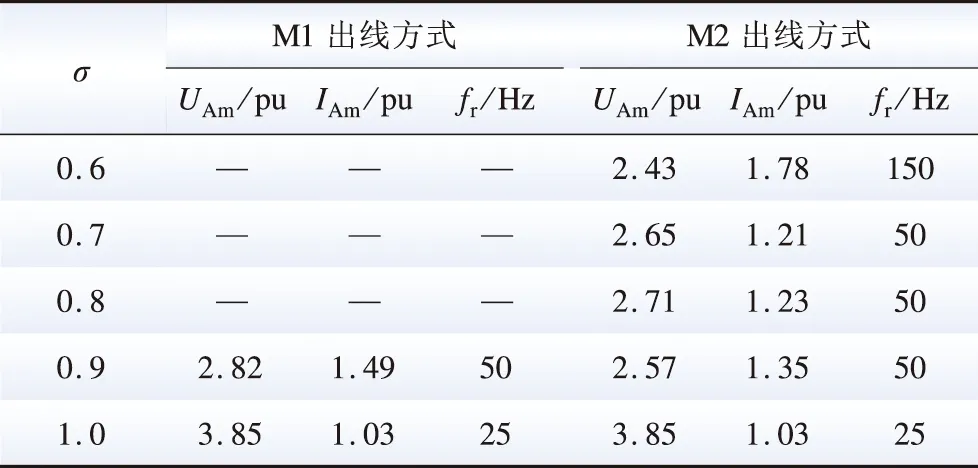
表3 铁磁谐振仿真结果(无合闸电阻)Table 3 Simulation results of ferromagnetic resonance (without closing resistance)

表3表明：1)M2出线方式更容易发生铁磁谐振。在σ=0.6～0.8时，M2出线方式发生了铁磁谐振，而M1出线方式未发生。这是因为，在相同的电缆线路占比下，M2出线方式下的换流母线对地电容更大，更容易与非线性变化的励磁电感发生并联谐振。2)无论M1还是M2出线方式，随着σ的增加，更容易发生铁磁谐振，铁磁谐振期间的换流变过电压倍数更大，而励磁电流略有下降。3)M2出线方式下，σ增加时相继发生的铁磁谐振频率有150 Hz的高频谐振、50 Hz的工频谐振和25 Hz的次同步频率谐振；而在M1出线方式下，σ=0.9、1.0时，分别发生了工频和次同步频率的铁磁谐振。这是因为，同样的励磁电感下，σ越大，换流母线对地电容越大，并联谐振的频率越低。

3.2.2 合闸电阻对铁磁谐振的影响

以M2(σ=0.8)方式为例，t1=0.5 s时断路器合闸，同时投入合闸电阻，换流变空投的仿真波形如图9所示。

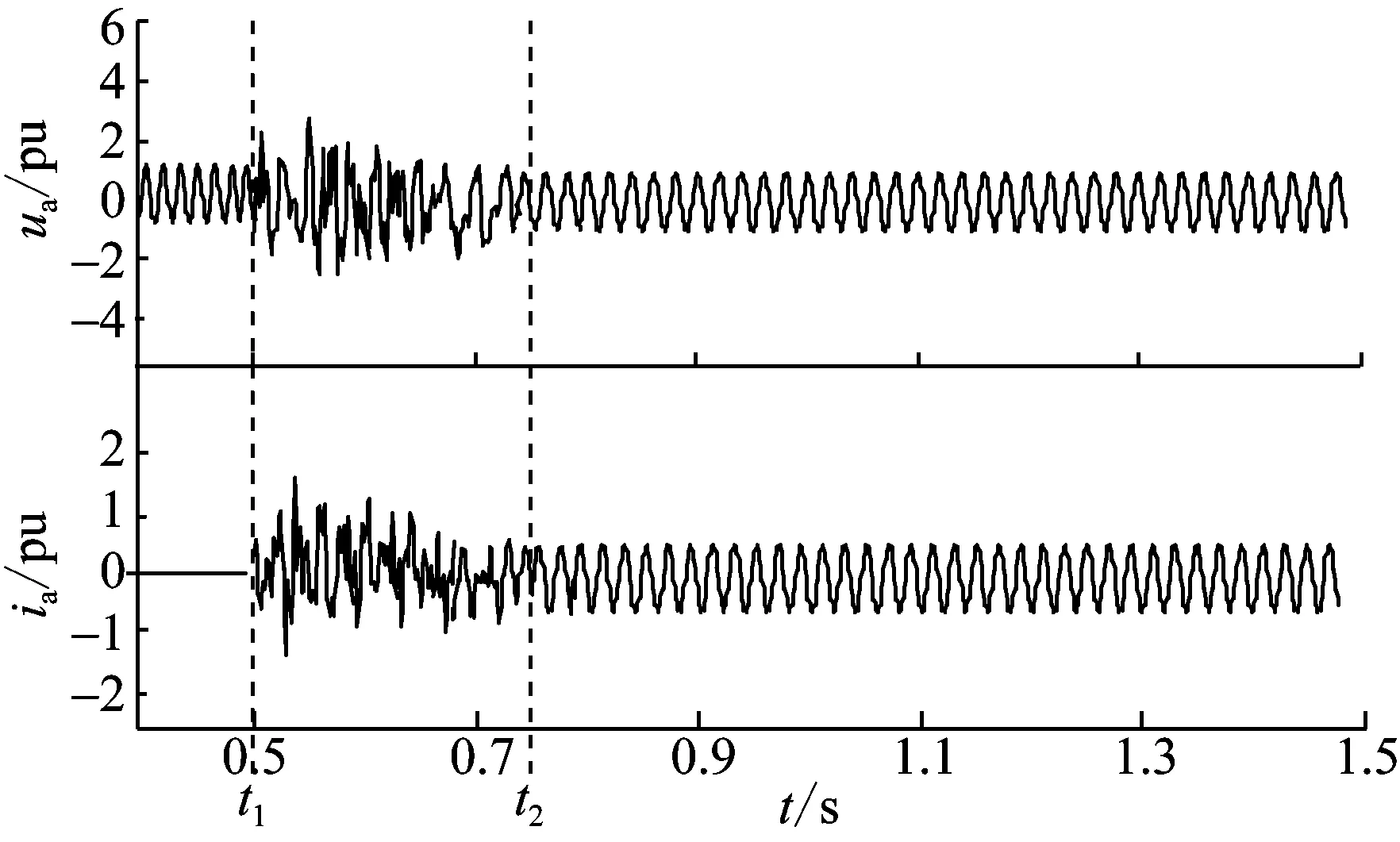
图9 M2(σ=0.8)换流母线电压电流波形(投入合闸电阻)Fig.9 Converter bus voltage and current waveform with closing resistance at M2 (σ =0.8)

由图9可以看出，经过约0.2 s的不稳定谐振，换流母线电压和空载电流趋向稳定的近似正弦波，其有效值接近额定值。表明合闸电阻提高了换流变空投电路的电气阻尼，有效抑制了铁磁谐振。上述结论对电缆线路占比在0～1.0范围内变化下的M1、M2 2种出线方式均成立。

综上所述，降低换流变空投引发的铁磁谐振概率的有效措施有：1)继续采用换流站架空线路的出线方式；2)换流站所接入的交流系统中，电缆线路占比不宜过高；3)投入合闸电阻。

4 结 论

换流变与所有大容量变压器一样，空投过程中可能出现励磁涌流和铁磁谐振，遭遇过电流和过电压的危害。研究表明：

1)换流变空投引发的励磁涌流。

(1)换流站由架空线路出线改为电缆线路出线后，励磁涌流峰值有所增加，衰减时间略有降低，但是改变幅度小，最大改变幅度在2%以内。因此，可以近似认为换流站无论采用架空线路还是电缆线路出线方式，不影响励磁涌流。

(2)抑制换流变励磁涌流的有效措施仍然是：投入合闸电阻、避免合闸角为0°和去磁。

2)换流变空投引发的铁磁谐振。

(1)与架空线路出线方式相比，换流站电缆线路出线方式更容易发生铁磁谐振，因此换流站不宜采用电缆线路出线方式。

(2)无论架空线路出线方式还是电缆线路出线方式，交流系统中的电缆线路占比越大，越容易发生铁磁谐振，而且谐振导致的过电压更严重，铁磁谐振的频率会降低。

(3)投入合闸电阻可有效抑制换流变空投引发铁磁谐振。