青岛市卫生技术人员变化趋势与预测模型研究

杨九龙 李宗遥

(青岛市市立医院，山东 青岛 266071 1 医院办公室； 2 门诊部)

卫生人力资源包括卫生技术人员、卫生管理人员以及卫生系统中的其他人员。作为社会人力资源的组成部分，卫生人力资源的数量和质量对国家或某个地区卫生服务水平有着直接影响，也反映了一个国家或地区的社会经济发展程度。因此，卫生人力资源是提高医疗卫生服务能力、促进卫生健康发展的关键[1]。卫生人力资源的重要性和特点要求卫生机构需要根据社会的卫生服务需求量来确定卫生服务过程中所需要投入的卫生人力资源，使之与卫生服务需求相适应，从而达到供给侧与需求侧平衡的状态。由此，卫生人力资源尤其是卫生技术人员的预测可为各级卫生部门制定中、长期卫生人力发展规划提供重要依据。预测卫生技术人员的方法有很多，包括人口统计学、流行病学以及计量经济学模型等。经典预测方法有卫生人力需要法、服务目标法、人力-人口比值法[2-3]。常用的计量模型有时间序列分析(ARIMA)模型、多元线性回归模型、主成分分析模型、灰色模型、加权平均组合模型等[4]。本研究对青岛市迈十几年卫生技术人员的变化趋势采用了ARIMA模型、多元线性回归模型、灰色(GM)模型进行预测[5-6]，以筛选预测青岛市卫生技术人员变化的最佳模型。

1 材料与方法

1.1 材料来源

收集2002—2015年青岛市卫生统计年鉴以及2016—2019年青岛市统计年鉴中的卫生技术人员信息，包括人均GDP、城市人均可支配收入、农民人均纯收入、青岛市户籍人口和常住人口估算值、卫生技术人员数量、患者平均住院日、实有床位、实际病床使用率等指标。其中青岛市户籍人口和常住人口估算值由于统计方式的改变，部分数据有缺失，采用平均增长速度的方法预测了缺失值。

1.2 研究方法

对2002—2015年卫生技术人员数量、患者平均住院日、实有床位数、农民人均纯收入的平均增长速度及环比增长速度参照文献[7]的方法进行计算；将上述各年数据采用Epidata 3.0软件进行录入，采用SPSS 21.0统计学软件构建ARIMA模型、多元线性回归模型，采用Excel公式编程构建灰色(GM)(1，1)模型[8]；利用构建的3种模型对2002—2015年卫生技术人员进行预测，将预测值与实际值进行比较，并计算相对误差绝对值以及平均相对误差绝对值，相对误差绝对值=|(实际值-预测值)|/实际值×100%。以平均相对误差绝对值最小的模型为最佳模型，采用最佳模型对青岛市2016—2019年的卫生技术人员进行预测。

2 结 果

2.1 青岛市卫生技术人员的基本情况

2002—2015年青岛市平均卫生技术人员数量为(43 388±13 106)人，整体呈现增长趋势，环比增长速度分别为23.42%、1.86%、3.05%、1.23%、-1.61%、8.43%、9.71%、7.63%、10.98%、14.76%、10.33%、4.48%、4.12%。2002—2015年卫生技术人员数量、患者平均住院日、实有床位以及农民人均纯收入的平均增长速度分别为7.39%、-1.90%、5.58%、12.82%。见表1。

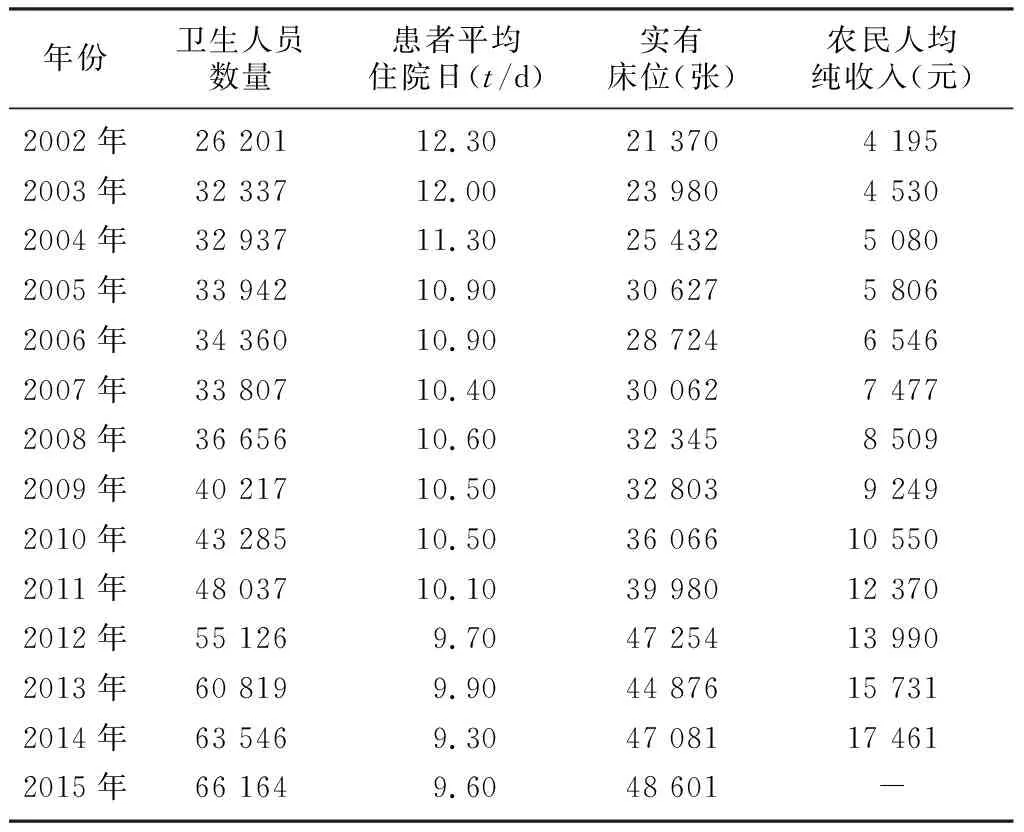
表1 2002—2015年青岛市卫生技术人员等的基本情况

2.2 预测模型的建立

2.2.1ARIMA模型建立 通过绘制序列散点图得知原始序列为非平稳序列。一阶差分后数据基本上分布在3 000人左右，说明为平稳序列，采用AIC和BIC准则定阶，最终创建ARIMA(0,1,0)模型来预测卫生技术人员数量。患者平均住院日、实有床位作为协变量纳入模型以后，获得平稳的R2=0.62，R2=0.99，R2>0.9，标准化的BIC为15.34,模型拟合较好。

2.2.2多元线性回归模型建立 用SPSS 21.0检验数据，绘制散点图和残差散点图，可见图形基本线性，数据都分布在(-2，2)之间，说明符合正态性和方差齐性。计算 Durbin-Watson 值为1.038，接近2，符合独立性。剔除具有共线性的变量，运用逐步法排除、筛选自变量。最后选取农民人均纯收入作为自变量，得到最佳模型：Y=16 897.49+2.65X1(R2=0.99，调整R2=0.97，F=331.66，P<0.01)，说明模型稳定。

2.2.3GM(1，1)模型建立 以2002—2015年青岛市卫生技术人员的数据作为原始样本数据，通过Excel进行计算，按照模型预测方法与公式求得a、b的估计值分别为-0.0765、25 332.9649，得到预测公式x∧(1)(k+1)=363 486.86e0.0765k-331 149.86。

2.3 各模型预测效果比较

应用上述构建的三种模型对2002—2015年青岛市卫生技术人员数量进行预测，对预测值和实际值进行比较显示，ARIMA(0,1,0)模型预测的相对误差绝对值最大值为4.93%，最小值为0.12%，平均相对误差绝对值为(2.72±0.02)%；多元线性回归模型预测相对误差绝对值最大值为10.66%，最小值为0.39%，平均相对误差绝对值为(4.82±0.04)%；GM(1，1)模型预测的相对误差绝对值最大值为12.25%，最小值为1.32%，平均相对误差绝对值为(5.25±0.03)%。比较分析各模型的预测结果，ARIMA(0,1,0)模型预测的平均相对误差绝对值最接近0，为最佳的预测模型。

2.4 ARIMA(0,1,0)模型对2016—2019年青岛市卫生技术人员预测结果

采用ARIMA(0,1,0)模型预测的2016—2019年青岛市卫生技术人员数分别为72 125、78 591、86 234、94 574人。2016—2019年实际拥有的卫生技术人员数量分别为69 169、76 146、83 975、90 631人，预测误差最少值为2.69%，最大值为4.66%，均值(3.71±0.92)%。

3 讨 论

根据收集到的结果，2002—2015年青岛市卫生技术人员整体呈现增长趋势，青岛市平均卫生技术人员数量为(43 388±13 106)人，平均增长速度为7.39%。本研究运用ARIMA(0,1,0)模型、多元线性回归、GM(1，1)模型3种模型拟合了2002—2015年青岛市卫生技术人员数，ARIMA(0,1,0)模型平均相对误差绝对值为(2.72±0.02)%；多元线性回归模型平均相对误差绝对值为(4.82±0.04)%；灰色模型平均相对误差绝对值为(5.25±0.03)%，拟合效果都比较好。

ARIMA模型是重要的时间序列分析模型[9]。由于卫生技术人员数量的实际预测中，数据大多是非平稳的，所以可以通过差分用ARIMA(p,d,q)模型来获得较好的预测结果[10-13]，优点在于对非平稳序列的差分处理使数据变为平稳序列后进行分析和预测[14]，适合在长期数据的基础上做短期预测[15]，能够兼顾数据的长期性和随机性。但ARIMA模型也有其局限性，即预测协变量的加入使得最终预测值准确度降低。可能由于个别年份医疗改革使得数据偏离，但平稳的R2越接近1表示拟合度越好，本研究构建的ARIMA(0,1,0)模型中平稳的R2为0.62，可能对预测结果有一定影响。

多元线性回归指用两个或多个自变量来预测或估计因变量，运用最小二乘法估计各个参数，相比较简单线性回归，预测更加有效，也更符合实际[16-17]。多元线性回归中，R2值越接近1，说明回归能解释的变异占比越大，拟合效果越好。本研究中的R2为0.99，接近1，说明本研究中多元线性回归模型拟合较好。但多元线性回归也存在与ARIMA模型同样的局限性；另外，社会经济因素是卫生人力资源的重要影响因素，自变量的选择具有一定的主观性，容易遗漏有价值的信息或强加因果；最后，多元线性回归还容易受到变量间交互作用的影响。

GM模型对样本量和数据的分布类型要求低，只要数据是非负单调就可以拟合，通过建立灰色微分预测模型，可预测事物的发展趋势[18]。卫生技术人员总数组成的序列样本量小、数据信息少且具有随机性，属于单调递增正值序列，可用于GM模型预测[19-20]。本研究构建的GM(1，1)模型预测方法简单、所需原始信息少、精确度高，适用于对卫生人力的预测。本研究中GM(1，1)模型误差百分比为4.85%，在5.00%以内，可以认为拟合度较好。GM模型也有其局限性，即没有考虑到其他因素对模型的影响而牺牲了一部分精度，因而不适用于外部因素影响较多以及长期的预测。

本研究结果显示，根据ARIMA(0,1,0)模型预计2019年青岛市卫生技术人员可达到94 574人，与实际拥有的卫生技术人数的误差仅为4.66%，模型预测的准确度较高。青岛市自2002年以来，除个别年份由于卫生政策的改变脱离正常范围外，卫生技术人员总体呈增长趋势。同期与国家卫生技术人员平均年增长率4.95%，和同期山东省卫生技术人员平均年增长率5.16%相比，青岛市卫生人员增长率均超出国家和省内水平。未来，随着经济、人口的增长，卫生技术人员也应有计划地增加，这就要求教育、人力部门做好卫生技术人员的规划，为青岛市培养数量充足的高素质卫生技术人员。同时，与之相配套的医疗机构数量、床位数及医疗设备等卫生资源也应及时补充。

本研究用青岛市2002—2015年的卫生技术人员及相关经济、卫生数据构建模型，数据资料的时间跨度长，利于构建模型的稳定，并采用3种不同的方法进行模型拟合并进行了比较，预测方法相对齐全。同时用2016—2019年青岛市卫生技术人员实际人数对模型预测效果进行了评价。本研究结果显示，ARIMA(0,1,0)模型平均相对误差绝对值最小，且相对误差均在5%以内，预测效果最优，建议在青岛市卫生技术人员变化趋势的预测中使用ARIMA(0,1,0)模型。