具有有理矩母函数跳分布的跳扩散模型下的动态基金保护定价

魏思媛，董迎辉

（苏州科技大学 数学科学学院，江苏 苏州215009）

由Gerber和Shiu[1]、Gerber和Pafumi[2]提出来的动态基金保护（Dynamic fund protectio，DFP）通过保险公司注入资金的方式为投资人在经济下行时期提供资金保护，以确保在合同期内投资人的基金价格始终高于某一预定的保护水平。近些年来，由于经济衰退，保险公司的偿付能力受到了投资人和监管机构的质疑，对这些提供保障水平的保险产品的定价问题的研究受到了广泛的关注。

Jin等[3]和Fan等[4]研究了基金价格服从马氏机制转换的几何布朗运动假设下的DFP的估值问题。刘孔洁等[5]给出了超指数跳扩散模型下动态保护基金的定价。Dong[6]在随机利率模型下提出了一个与债券价格有关的随机保护水平。许超和董迎辉[7]放松了文献[5]中的常数保护水平的假设，提出了用一个跳扩散模型来刻画障碍水平，在超指数跳扩散模型和随机障碍下，研究了动态基金保护的定价问题。尽管超指数分布可以用来逼近许多分布，包括Gamma分布、Weibull分布和Pareto分布，然而，由于超指数分布是由指数分布密度的线性组合所决定的概率分布，其权重均不能取负值，所以Cai和Kou[8]指出，超指数分布只能用来解决一些具有绝对单调性质的分布。众所周知，在一般的跳扩散模型下人们很难解决定价问题[9－10]。具有有理矩母函数的分布是一类比超指数分布更为广泛的分布，它们可以用来近似任意的分布，并且在具有有理矩母函数跳分布的跳扩散模型下，仍能得到动态基金保护的定价公式。Dong和Wang[11]在具有有理矩母函数跳分布的跳扩散模型下得到了参与分红寿险合同的定价，然而动态基金保护的产品比参与分红寿险要复杂的多，其定价问题也更为复杂。笔者将在具有有理矩母函数跳分布的跳扩散模型和随机障碍下研究动态基金保护的定价问题。

论文结构安排如下：第一部分介绍动态基金保护和定价模型；第二部分在具有有理矩母函数跳分布的跳扩散模型和随机障碍下给出DPF价格的拉普拉斯变换的显示解；第三部分对全文进行总结。

1 模型

设{Ω，ζ，{ζt}0≤t≤T，Q}为带滤子的完备概率空间，其中{ζt}0≤t≤T为满足通常条件的滤子，T＜∞。假设所有随机变量和随机过程均定义在该概率空间上且关于ζT可测，Q为风险中性鞅测度。

令{N（t），t≥0}表示时间[0，t]内引起基金价格发生跳跃的事件的来到过程，假设{N（t），t≥0}是强度为λ的泊松过程。假设基金价格服从如下的跳扩散过程

其中F（0）＞0是初始基金价格，σ1＞0是扩散系数，{W（t），t≥0}是一个Q测度下的标准布朗运动是独立同分布的随机变量序列，其密度具有有理的矩母函数

其中0＜p，q＜1，p+q=1，mi，m∈N+，并且是两个至多M-1次的多项式函是无风险利率数，并且满足

利用部分分式分解，由矩母函数f^1（s）可得到{Zi（1），i≥1}的共同密度为

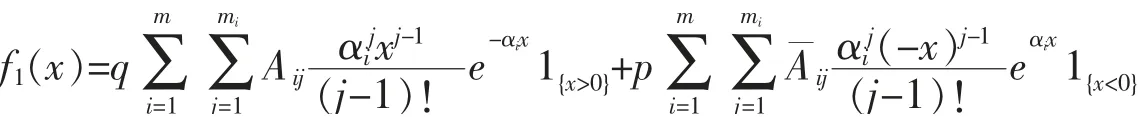
其中

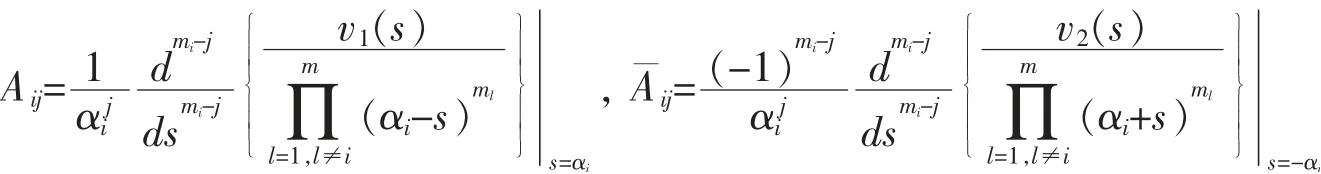
假设保护水平服从双指数跳扩散过程

其中σ2＞0为常数是独立同分布的随机变量序列，其密度函数为

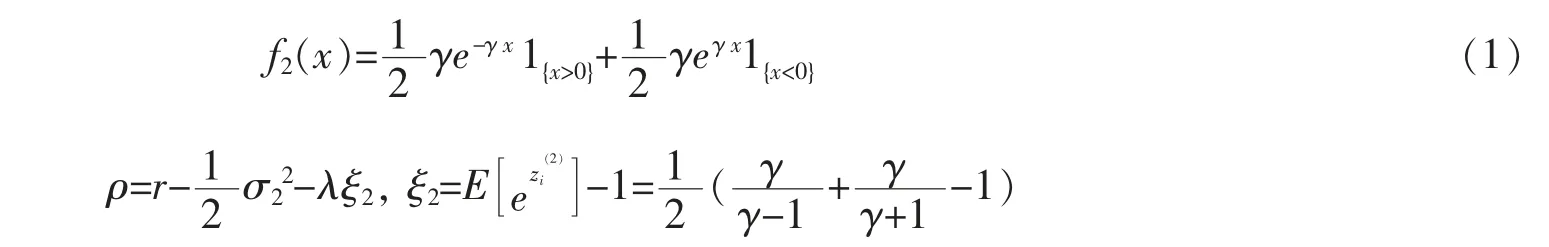
注1若假设随机障碍也服从一个与资产价格过程相关的具有有理矩母函数跳分布的跳扩散过程，也可以用同样的理论方法来解决动态基金保护的定价问题，然而这只会导致计算上复杂而不会带来任何理论上的创新。因此,为简便起见，文中仅考虑引起资产价格和障碍水平发生跳跃的事件来到过程服从相同的泊松过程，且障碍水平的跳分布服从双指数分布。

令

定义最小值过程为

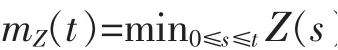
令y＜0为一给定常数，定义首中时为

显然，

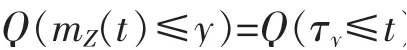
2 动态基金保护的估值

令DF（F（0），T）为具有到期日为T的动态基金保护合同所提供的动态基金保护在0时刻的价格，则根据资产定价的基本定理，有

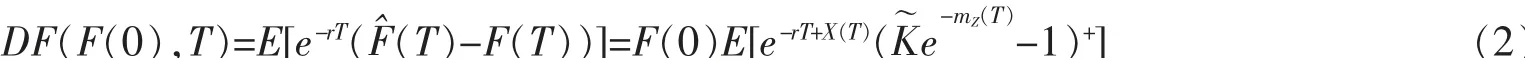
为了计算（2）式的表达式，利用Radon-Nikodym导数，定义一个新的测度Q~

由Girsanov定理，可以得到如下结论。

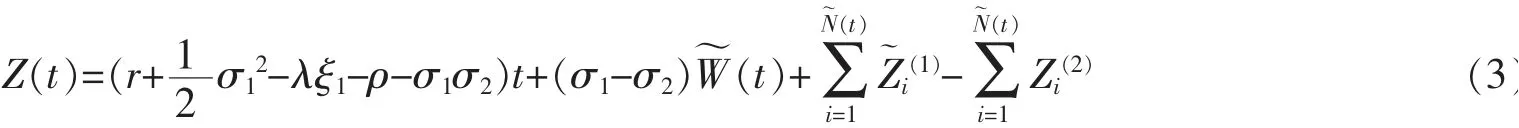
其中

证明 利用跳扩散过程的Girsanov定理即得结论。

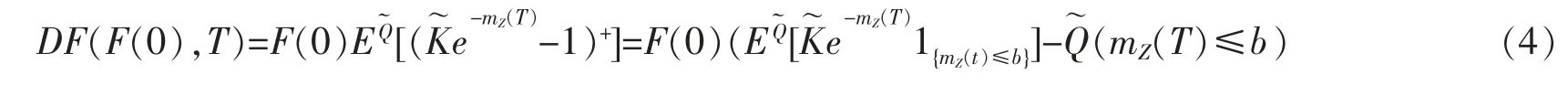
以下的结论对推导动态基金保护价格的表达公式起着非常重要的作用。

引理2令

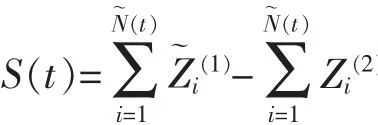
则S（t）是一个参数为λ~的复合泊松过程，其密度函数为

其中

证明

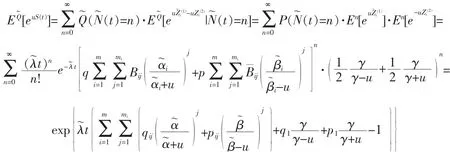
于是，由矩母函数和分布的一一对应，结论得证。

其中复数x满足E[exZ（1）]＜∞。由Levy-Khinchine公式得

引理3令Z为公式（3）中给出的具有有理矩母函数跳分布的跳扩散过程。对任意的δ＞0，y＞0，τy的拉普拉斯变换为

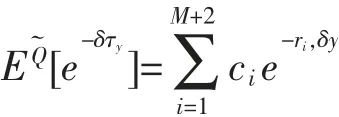
其中r1，δ＞r2，δ＞…＞rM+2，δ是下面方程（6）的M+2互不相同的负根

系数c1，c2，…，cM+2满足下列方程组

证明 参见文献[11]中的式（3.29）。

引理4对任意的T＞0，有

证明 证明过程类似文献[7]中的引理2.6。令

当y→-∞时，可见引理结果成立。

由引理3和引理4，可以推导出DF（F（0），T）的拉普拉斯变换。

定理1对任意的δ＞0，DF（F（0），T）的拉普拉斯变换为

证明 由公式（4）可得

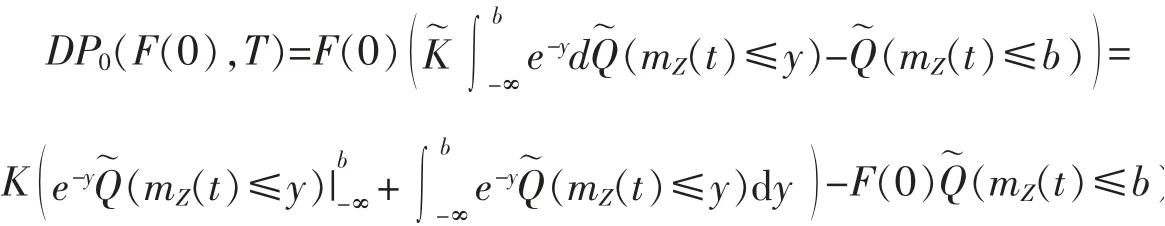
由引理4可以得到DP0（F（0），T）的拉普拉斯变换为

3 结语

笔者用一个具有有理矩母函数跳分布的跳扩散模型来刻画资产价格过程，该过程能够用来近似任意的跳扩散过程，并且在该模型下，可以得到首中时的拉普拉斯变换。进一步，笔者给出了具有有理矩母函数跳分布的跳扩散模型下动态基金保护价格的拉普拉斯变换。