一类非线性热传导方程的数值解法
高忠社
(天水师范学院 数学与统计学院,甘肃 天水741001)
1 非线性热传导方程
热量的传播是发生在存在温度差的同一物体或者物体之间,热量从高温物体传到低温物体的过程,就叫做热传导。而在实际应用中有时需要考虑隔热问题,有时需要考虑散热问题,从而尽量有效控制热量的传播。这种热传导现象利用数学方法描述,就得到了热传导方程。
在实际应用中,对于单个设备的热传导问题相对比较容易进行模拟与仿真,但是关于结构比较复杂的热传导问题、包含大量设备的复杂的多尺度系统的导热问题等,其模拟仿真仍是十分困难的课题,比如复杂电路板的热传导问题。
文献[1-4]中H.S.Carslaw,J.Lienemann等人给出了热传导问题的非线性模型,S.M.Filipov等人研究了一般形式的非线性热传导方程的计算问题。 由于不同材料导热系数随着温度的变化而不同,笔者将研究一类具有指数型热传导系数的热传导方程的计算问题,对于时间方向使用隐式Euler差分格式,空间方向使用二阶中心差分格式。 利用Taylor级数方法得到该差分格式的误差阶为O(τ+h2),对于离散化后的代数方程组利用Newton迭代法进行求解,最后通过数值算例分析讨论了该方法的可行性。
该文将研究具有非线性导热系数的一维热传导问题,假设热源在最左端,热量沿着细棒传播,不考虑其他形式热量传播,如图1所示。

图1 热传导问题分析示意图
在科学工程领域中,为了控制热量的传播而建立了一类具有非线性的热传导方程[1-3]

其中u(x,t)表示在(x,t)处的温度,ρ为材料密度,Cp是材料的热容量,k(u)(u表示温度)为热传导系数,即它与温度有关,所得方程是典型的非线性热传导方程。
由方程(1)可得

如果k(u)和u无关,有,方程(1)是经典的线性抛物型偏微分方程,方程(2)为非线性的抛物型偏微分方程。
在半导体材料的导热等很多热传导问题中,由于热传导系数随着温度的改变而改变,所以热传导系数通常是一个与温度有关的函数。 如半导体材料的热容量远远小于导热系数,在实验测定中发现,热传导系数近似于指数的变化,设

由于k0是非零的正常数,因此,只需考虑下列形式的一类非线性热传导方程

对方程(3)化简,可得
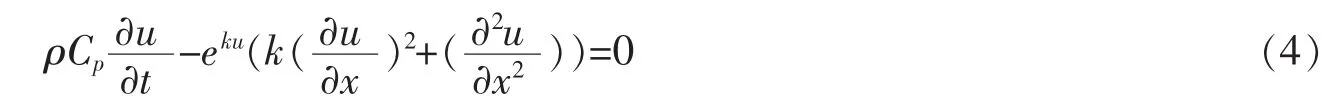
设方程(1)在有限闭区间[a,b]上,满足初边值条件

其中边值条件(5)给出了在区间两端关于时间的温度分布函数,初始条件(6)给出了在初始时刻的温度分布情况。
2 时间方向的隐式Euler方法离散
对于∂k(u)/∂u=0线性的热传导方程已经有很多数值方法[5-7],如有限差分法、有限元法等。在文献[3]的启发下,将对方程(4)及初边值条件(5)、(6),在时间方向使用隐式的Euler方法进行离散化。
设时间方向的步长为τ,时间t>0,使用等距的划分

对方程(4)利用隐式Euler方法进行离散化,则有

其中un=un(x),un-1=un-1(x)分别表示u(x,tn)和u(x,tn-1)的近似值。
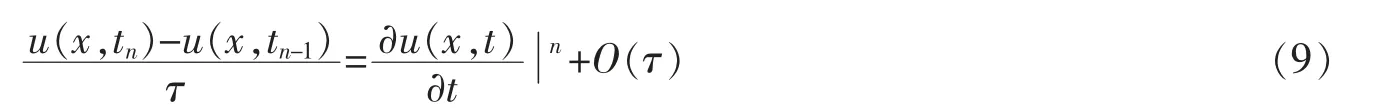
为了求解方程(8),设vn=dun/dx

则方程(8)变形为
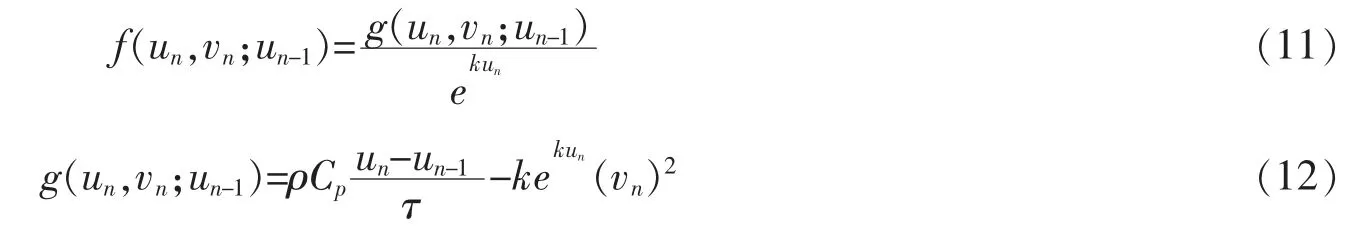
根据式(5),边值条件可以离散为

这样式(11)、(12)、(13)组成了一个关于未知量为un的非线性两点边值问题。
3 空间方向的二阶离散方法
设在区间[a,b]上等距划分[8-10],即

对式(10)中的二阶导数,用二阶中心差分算子

方程(10)可表示为
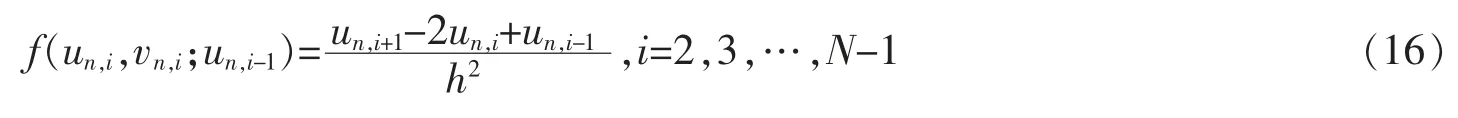
其中un,i+1,un,i,un,i-1分别是un(xi+1),un(xi),un(xi-1)的近似值。即温度函数u(x,t)在点(xi,tn)的近似值。
而

其中

根据式(13)及边值条件(16),得到下列方程组

4 差分格式的误差分析
根据文献[11-12],对于上述的差分格式进行误差估计,由式(8)、(15)、(18),有

其中un,i表示u(xi,tn)的近似值。
对于上式中各项在(xi,tn)处Taylor级数展开

则有

将由式(21)、(22)、(23)代入式(20)整理,将式(20)与式(8)相减可得,截断误差
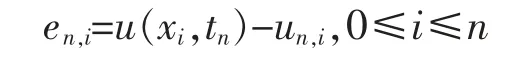
满足

5 非线性方程组的牛顿迭代法求解
对式(19)用非线性牛顿迭代法进行求解,建立N行的列向量

其中
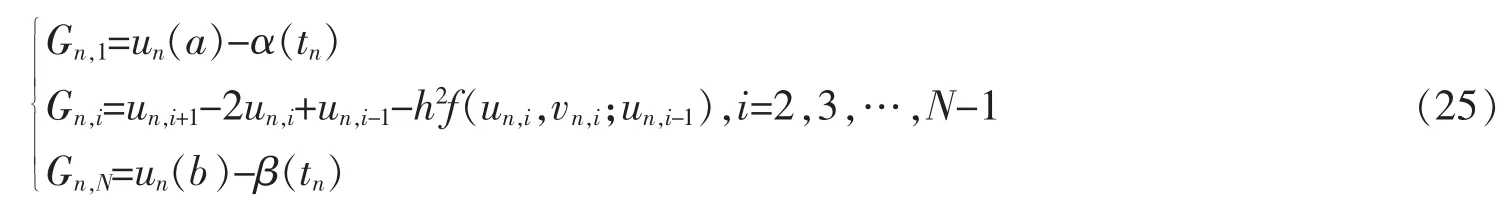
则有

其中

给定初值un(0),对非线性方程组(26)利用牛顿迭代法求解

其中Jn(k)是Gn的Jacobian矩阵,即

方程组(25)中第二式中f(un,i,vn,i;un,i-1),i=2,3,…,N-1,与un,i,vn,i有关,为了分析Jacobian矩阵元素,先求f(un,i,vn,i;un,i-1),i=2,3,…,N-1关于un,i,vn,i的偏导数。
记fn=f(un,i,vn,i;un,i-1),gn=g(un,i,vn,i;un,i-1),而qn=q(un,i,vn,i;un,i-1)和pn=p(un,i,vn,i;un,i-1)分别表示fn关于un,i,vn,i的偏导数,即

其中

将式(32)、(33)代入式(30)、(31),则有

综合分析,可得Jacobian矩阵的元素

式(28)是一步两层迭代格式,给定初值un(0),可得近似迭代解{un(k+1)}。如果此序列收敛,可得该向量序列的极限是非线性代数方程组的解。在实际的计算中通常使用||un(k+1)-un(k)||<ε结束迭代过程。
6 算例
考虑均质细杆的热传导问题,以细杆建立x轴,假设均质细杆介于x=0与x=2之间,热源在坐标原点处,不考虑其他形式热量传播,设物体密度ρ和热容比Cp都是常数,热传导系数和物体的温度有关,即

假定物体密度ρ=1、热容比Cp=1和k0=0.1,物体在两端的温度为常数,即

初始温度分布满足

则式(4)、(38)、(39)构成非线性热传导方程的初边值问题。根据文中上述方法,可得该问题的数值解,其中给定空间方向x∈[0,2],步长h=0.05,时间步长τ=0.5,时间t∈[0,15],指数参数k=-1,0,1时给出了三维图形和u关于x的图形,如图2、图3、图4所示。

图2 导热参数k=-1热传导三维图形和u对x平面图形

图3 导热参数k=0热传导三维图形和u对x平面图形

图4 导热参数k=1热传导三维图形和u对x平面图形
7 结语
热传导方程是一个经典的抛物方程,同时该方程也广泛应用于很多科学工程领域。 文中根据文献[3]讨论的一般类型非线性热传导问题,讨论了一类具有指数型热传导系数的热传导方程的计算问题。由于很多材料的导热系数随着温度的不同而不同,文中主要研究了热传导系数为k(u)=k0eku的非线性热传导方程的数值解法。 其中时间方向利用隐式Euler差分格式、空间方向利用二阶中心差分格式进行离散化,同时得到该差分格式的误差阶为O(τ+h2),离散化后的代数方程组用Newton迭代法进行求解。 最后通过数值算例,说明该方法具有一定的可行性和实用性。

