由感悟思想到培养能力——小学生数学推理能力的培养

福建省晋江市磁灶教委办 蔡文康

福建省晋江市磁灶镇官田小学 许文洞

《义务教育小学数学课程标准（2011年版）》提出“四基”，进一步明确将感悟数学思想方法作为数学课程整体目标的一个有机组成部分。的确，数学课堂固然应该教会学生许多必要的知识，但更重要的是让学生在学习这些知识的过程中获得数学思想。对数学思想的感悟，能指引学生学会用数学观点去思考问题和解决问题，有助于他们数学思维能力及良好思维品质的养成。

推理作为重要的数学思想方法之一，是数学基本的思维方式，在生活中有着广泛的应用。王永春教授在《小学数学与数学思想方法》一书中指出：“在小学数学中，除了运算是数学的基本操作方式外，推理也是常用的操作方式。无论是低年级的找规律，总结计算法则，还是高年级的面积、体积公式的推导，无不用到推理的思想方法。因而，广大教师要牢记推理思想从一年级起就要开始渗透和应用，是一个长期的培养过程。”在教学中，教师如能关注推理思想的渗透，重视培养学生的推理能力，既有利于帮助学生形成言必有据、一丝不苟的良好习惯，也有利于学生掌握科学的思维方法，对学生思维能力的提高有着积极的促进作用。

通过参与“基于核心素养发展的小学生数学推理能力培养策略研究”课题实验，对于引导学生感悟推理思想，培养学生的推理能力，我有如下几点思考。

一、练习说理，在有理有据的思考中感悟

在教学中，我们会发现学生在解题时不经意就会用到演绎推理，他们在判断或选择的时候，通常有着自己的“因为……所以……”。因此，我们要对学生的回答多问为什么，引导学生学会清楚地表达自己的思考过程，表达自己做出判断、得到结论的依据，也就是让学生说理，养成推理有据的好习惯。语言是思维的外衣，回答问题是学生组织语言的过程，也是培养学生如何判断的推理过程。在表达逐渐清晰完整的过程中，学生的思维会逐渐完善；而教师有意识地引导和培养，会让学生逐步学会有条理、有根据地思考问题，在无形中达到推理思想的渗透。例如：在一年级下册“退位减法计算”教学中，对于“25-8”的计算方法，学生通常会直接表达“先算15-8=7，再算10+7=17”。其实这个计算过程也是一个推理的过程，这时教师应引导学生明确推算的过程，并进行说理表达：“25可以分成10和15，因 为15-8=7，10+7=17，所 以25-8=17。”又如二年级下册，学习了更大的数的计算之后，经常出现估一估的问题。在判断“林场今年植树总数够800棵吗”的时候，也需要进行推理。这时候教师应引导学生认识推理的过程并进行完整的说理表达：“把316看作320，把435看作440，320+440=760，因为320+440＜800，推出316+435＜800，所以植树总数肯定不够。”诸如此类蕴含着推理过程的问题还有很多，在教学中，教师要有意识、有计划地进行数学说理表达训练。比如：提供示范或者提供说理表达的模板，引导学生从模仿起步练习表达；在训练过程中，从要求“说完整”，到要求“说准确”，再到“说简单、清晰”，逐步提高说理表达的要求等。当学生能够清晰、完整、有条理地表达自己的想法时，他们的推理能力也将得到提升。

二、亲历探究，在观察、实验、猜想、验证中感悟

推理思想的获取是靠学生“悟”出来的，而不是靠教师“教”出来的；是从“量”的积累，达到“质”的飞跃，不是一两节课和一两天就能获取的。因此，在课堂教学中，教师要结合教学内容不断给学生提供丰富的、有挑战性的观察、实验、猜想、验证等活动，让他们在探索知识、回顾总结获得知识的方法和步骤中，不断“意识”，逐渐“感悟”。

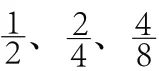
同时，在教学中，我们还要注重引导学生以事实、经验为基础，发现问题、提出问题，大胆“假设”，合理“猜想”。如教学小数乘法时，以“0.15×3”为例，不用情境，直接出示算题，引导学生根据已有知识经验猜想“0.15×3”的计算方法，多数学生会想到先算15×3，再添上小数点，并提出确定积的小数部分位数的猜想。再引导学生借助生活情境解释、画图说明等方式验证猜想，让学生经历合情推理的过程，感受探索发现的乐趣。再如圆锥体积公式的学习，先让学生回顾已学的长方体、正方体和圆柱的体积计算公式，3个形体的体积计算公式可以统一为“底面积×高”。接着引导学生进行类比猜想：怎么得出圆锥的体积与高？再引导学生回顾圆柱体积公式的推导方法，明确转化前后的圆柱体与长方体等底等高的关系。此时，引导学生思考：为了求圆锥的体积，可以让它转化成哪种立体图形？用什么方法进行实验？在学生提出用倒水或倒沙子的方法时，再引导学生思考：对用来装水或沙子的圆锥、圆柱或长方体容器的大小，你有什么想法？在多次的猜想与思辨之后，再让学生进行操作验证，获得结论。实践证明，结合教学内容反复经历观察、实验、猜想、验证的探究过程，学生对推理思想的感悟更深刻，也有效促进了学生推理能力的提高。

三、总结提升，在画龙点睛之语中感悟

推理思想相对于知识技能来说是“隐形的”“缄默的”，它蕴含在具体的数学内容中，要让学生意识和感悟到探索过程之后的总结提升是必不可少的。这时，教师的引导性小结就显得尤为重要了。以“分数的基本性质”为例，教师在总结里可进行如下引导：“根据知识间的密切关系展开大胆的猜想，再观察操作，小心验证，这就是数学家发现真理的过程，只要我们敢于根据知识之间的关系，进行大胆猜想，并能仔细观察、小心验证，将来我们也能发现新的规律和性质。”又如：在“图形中的规律”一课总结时，可做如下引导：“刚才我们初见这个问题时感觉它很复杂，遇到复杂的问题时我们采取了什么样的解决问题的策略？当我们从简单的例子中归纳出规律时，我们就可以利用这个规律解决复杂的问题了。”再如：探索完“整十数除以一位数”的口算方法后，教师可这样引导：“通过‘转化’我们解决了整十数除以一位数的口算问题，‘转化’是帮助我们解决问题的好方法，今后我们遇到新问题无法解决时，就想想能否把它转化为我们学过的知识来帮助我们解决问题。”教师的引导性小结，可将要渗透的推理思想及方法提升并外显出来，达到画龙点睛的效用，使学生的感悟更为深刻。

总之，在教学中，教师应以数学知识为载体，在观察、实验、猜想、证明、综合实践等数学活动中，不断引导学生通过富有逻辑的思维过程和清晰的数学表达体验和感悟推理思想，帮助他们逐渐领会推理的思维方法，切实促进学生推理能力和数学素养的形成和提高。