矩阵SVD分解在大学生体育成绩方面的指导作用研究

周红波

(北京工业大学 体育教学部，北京 100124)

1 问题的提出

在信息爆炸的大数据时代，处理海量数据并从中获得有用信息是所有领域的共同需求。大量的高维数据给人们利用带来了许多困难。(1)维数灾难：要让智能系统有足够的学习能力，需要样本个数至少比样本维数高出一个数量级。然而当样本维数过高时，人们很难收集到足够的样本；(2)算法失效：高维数据的运算可能使得运算得次数几何级数增长，从而导致算法失效。要解决这些问题，如何对高维数据进行降维显得尤其重要。

由于矩阵SVD分解(Singular Value Decomposition，奇异值分解)具有全局最优的数据重构能力，且具有转置不变性、位移不变性、旋转不变性和镜像变换不变性等重要性质，因此，在众多研究领域都被作为非常有效的降维方法。其中PCA(Principal Components Analysis，主成分分析)方法又称Karhunen-Loeve变换或Hotelling变换，它是以矩阵SVD分解为基础的有效特征提取方法之一。

对于任意m×n矩阵，想要将其对角化，SVD分解是一个很好的选择。下文首先介绍矩阵的SVD分解。

定义1.1[2]设A为n×n方阵，α为一非零向量，若存在常数λ使Aα=λα成立，则称λ为A的一个特征值，α为A的对应于特征值λ的特征向量。

对于任意的n×n对称矩阵必可以由其特征值与特征向量对角化[2]，而对于非对称的m×n矩阵A，可以考虑ATA，由于其必定为n×n的对称矩阵，从而可以对角化。

设A为m×n的矩阵，令v1,v2,…,vn为ATA的单位正交的特征向量，对应的特征值分别为λ1，λ2，…，λn，则有：

即ATA所有特征值均非负，从而可以将其由小到大重新排序，排序后使得特征值满足：

λ1≥λ2≥…≥λn≥0。

定义1.2[3]矩阵A的奇异值是ATA的特征值的平方根，记为σ1，σ2，…，σn。

定理1.1[3]设A是的m×n的矩阵，那么存在一个m×m的正交矩阵U和一个n×n的正交矩阵V使得A=UΣVT，其中Σ=diag{σ1,σ2,…,σr,0…,0}为一对角阵，r为矩阵A的秩。其中，矩阵U和V分别称为A的左奇异向量矩阵与右奇异向量矩阵，且不由A唯一确定。

2 SVD分解的应用—CPA分析

主成分分析的具体方法是对变量的协方差矩阵或相关系数矩阵求奇异值和奇异向量，从下面的定理将看到，对应最大奇异值的奇异向量，其方向正是协方差矩阵变异最大的方向，依次类推，第二大奇异值对应的奇异向量，是与第一个特征奇异正交、且能最大程度解释数据剩余变异的方向，而每个奇异值的大小则能够衡量各方向上变异的程度。

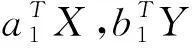
关于上述定义，容易得到：

(1)规范性条件D(αTX)=D(βTY)=1不影响ρ(αTX，βTY)的最大值。

若ΣX,ΣY,ΣXY分别表示随机向量

X=(X1,…,Xp1)T∈Rp1，

Y=(Y1,…,Yp2)T∈Rp2

的方差矩阵及X与Y间的协方差矩阵为两个随机向量，且满足ΣX，ΣY>0，则下述定理表明典型相关方向、典型相关变量、典型相关系数是存在的。

有关主成分分析理论上有如下结论。

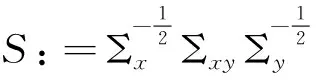
其中U=(u1,…,up1)∈Op1,V=(v1,…,vp2)∈Op2分别为S左、右奇异矩阵，r为S的秩，则

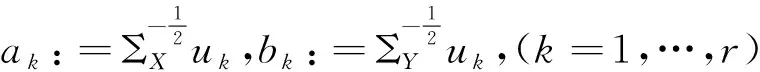
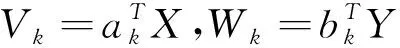
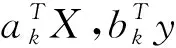
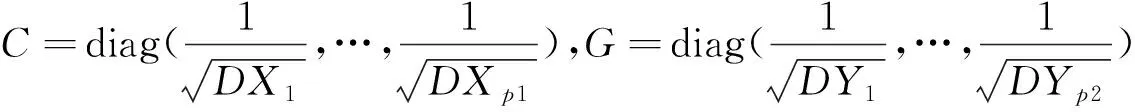
X*=C(X-μ1)，Y*=G(Y-μ2)则有

下述定理表明，从相关矩阵出发，一方面可以求出标准化之后的随机向量X*，Y*间的典型相关方向、典型相关系数、典型相关变量。另一方面，也可以据此推出标准化之前X，Y的典型相关方向、典型相关系数、典型相关变量。

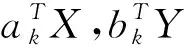
3 实例分析

例3.1某班有20名学生，设X1:平均每周锻炼的时间，X2:平均每周玩游戏的时间，X3:平均起床是晚于7：30的时间，Y1:体育课成绩大于90分，Y2:体育课成绩小于75分。目标是研究锻炼时间、玩游戏时间、起床时间与体育课成绩之间的关系。

数据分析如下的矩阵计算将由Matlab具体实现[4-5]。

根据所测数据计算随机变量X1X2X3Y1Y2之间相关系数矩阵为

R=

从而令

进一步，求得S的奇异值分解为

S：=UΔVT=

因此，典型相关方向构成的矩阵为

(1)由S的表达式看出：第一对典型变量V1，W1的相关系数为0.8549，说明相关性非常显著。且第一对典型相关变量V1，W1的表达式为：

V1=-1.2862X1+0.2720X2-0.4893X3,W1=-0.9306Y1+0.2324Y2。

从上述表达式中可以看出：X1和X2的系数绝对值分别最大且符号相同，这表明每周锻炼时间越长体育成绩越优秀。

(2)第二对典型变量V2，W2的相关系数为0.6732， 说明相关性比较显著。且第二对典型相关变量V2，W2的表达式为：

V2=-0.1983X1-0.9768X2+0.1347X3,W2=-0.4116Y1-0.9907Y2。

由于V2，W2表达式中X2和Y2系数绝对值最大且符号相同，表明玩游戏时间越长体育课成绩不及格的可能性越大。

例3.2为了解家庭的情况与学生成绩之间的关系，为此调查了20个学生。假设X1:体育测试成绩，X2:体育课成绩，Y1:在校月支出(百元)，Y2:来自城市(1表示来自一线城市、2表示来自二线城市、3表示来自三线城市、4来自农村)，Y3: 家庭的年收入(万元)。

数据分析如下的矩阵计算由Matlab实现[4-5]。根据所测数据计算随机变量X1，X2，Y1，Y2，Y3之间相关系数矩阵为

由上述矩阵R可计算：

从而，

进一步， 矩阵S的奇异值分解为

S:=UΔVT=

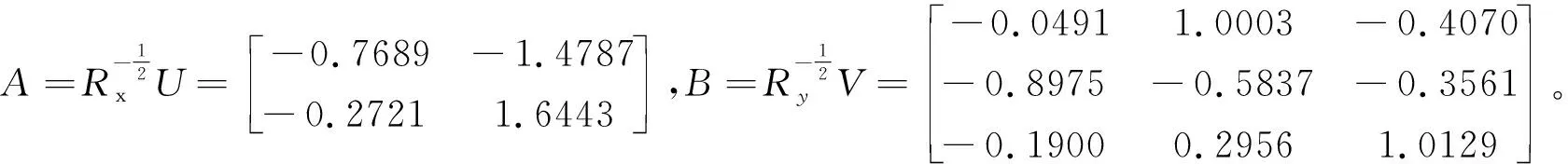
(1)由S的表达式可看出：第一对典型变量V1，W1的相关系数为0.6879， 相关性较显著.另外，第一对典型相关变量V1，W1的表达式为

V1=0.7689X1+0.2721X2,W1=0.0491Y1+0.8975Y2+0.1900Y3。

从上述表达式可以看出：X1和Y2的系数的绝对值在第一对典型变量V1，W1的系数很大，而且符号是一样的，说明家庭年收入较高者，体育测试成绩相对较好。这可能由于体育测试成绩主要侧重考察学生的耐力、力量等方面，而不是有关某些技巧。

(2)由于第二对典型相关变量V2，W2的相关系数为0.1869，说明变量间相关性几乎没有。

4 结语

矩阵的SVD分解具有全局最优意义上的数据处理能力，主要体现在两个方面：一是SVD分解可以有效提取信息的主要部分，即能达到降维目的又可以最大限度地保证原始数据的完整性；二是SVD分解无任何参数限制，在计算过程中不需要进行干预，这样得到的结果仅与数据相关而与用户独立。

鉴于上述优点，本文基于矩阵SVD分解，利用PCA分析方法，把理论结果与实际案例相结合，分析有关因素在大学生体育成绩中的作用，所得结果对实际教学具有一定的指导作用。