Python动画辅助大数定律的数学实验

孙晓玲，王 宁

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

概率论与数理统计是高校理工科和经济类专业重要的公共基础课程，旨在训练学生用概率思想处理随机事件，进一步学会利用统计方法去处理数据资料。随着金融类和大数据类专业的快速发展，概率论、数理统计和随机过程等课程成为高校教学研究的重点内容。

大数定律在概率论与数理统计课程中的教学特点是内容抽象，理论较强，在实际统计工作中应用非常广泛。在教学安排中，大数定律一般位于学期教学末尾，教学内容枯燥抽象，同时，随机序列的极限难以计算，学生理解起来较为困难。大数定律由概率的统计定义引申而来，在课程中具有非常重要的地位，随机变量的动态变化在教学过程中难以进行直观的展示。为了增强教学效果，帮助学生把握大数定律的理论和应用，可以借助软件模拟随机数列中的统计规律性。软件辅助教学可以充分体现定理中的动态变化过程，教师通过图形和动画讲授大数定律的基本思想，可以让学生形成对新方法的直观理解，相关教学资源的开发成为促进概率教学的重要研究方向[1-2]。

1 Python简介

Python是支持面向对象、动态数据类型的高级程序设计语言，功能强大且资源免费。另外，由于Python语言可移植性强，其代码可以在手机端编写和运行，这为学生自学数学实验提供了便利的环境。

Python用于概率统计的程序库主要有numpy和matplotlib，它们分别可被用于数值运算和可视化操作。Python代码语法简单，可读性强，编写简易，具有强大的图形和动画编程功能，方便演示数学思想，有利于学生自主进行代码的学习和开发。

利用Python对大数定律进行随机模拟，并生成动画或者视频，结合计算机可视化方法丰富教学手段，在课程的教学中可以加深学生对教学内容的理解，增强学习兴趣。利用软件进行概率统计的数学实验，对培育大学生学以致用的学习能力、推动概率论与数理统计的教学改革具有一定的现实意义。另外，动态视频在学习过程中还能让学生深刻理解理论的变化过程，有助于将理论应用于实践中，Python代码的学习还能提高学生运用计算机应用软件的能力，体现学以致用的思想[3-4]。

2 大数定律极限思想

在中心极限定理和大数定律表述中，随机变量和的极限出现次数比较多，在概率理论中，随机变量X1，X2，…，Xn和的分布计算非常复杂，对其极限的讨论也非常困难。引入极限思想后，发现在很一般的情形下，和的极限分布就是正态分布，从而可以通过极限方法得到中心极限定理的相关结论。另一方面，由伯努利实验引出的概率的统计定义和大数定律也可以使用极限思想进行理论探讨，从而得到几个大数定律的结论。

大数定律的一般结论：设有随机变量序列{Xn}，如果对任意ε>0，有

则称该随机变量序列服从大数定律。大数定律的结论是概率意义上的，根据给定的随机变量序列满足的条件不同得到不同的大数定律，如切比雪夫大数定律、马尔科夫大数定律、辛钦大数定律等。

大数定律来自于对随机事件的大量观测，是对“平均值的稳定性”这一事实的理论表述，在教学过程中定理的证明并不复杂，但其中包含的极限过程的动态刻画不容易讲解。在学习过程中，学生能记住大数定律的基本结论，但是对其应用和含义的理解不够透彻，随着n无限增加时，大数定律的极限中概率值的变化趋势难以形象化。借助数学实验的思想方法可以有效解决大数定律教学过程中的这两个难点[5-6]。

3 大数定律的数学实验

数学实验把计算机技术和数学软件引入课程教学，以提高学生学习数学的积极性和对数学的应用意识，培养学生用所学的数学知识和计算机技术去认识问题和解决实际问题的能力，激发学生独立思考、主动探求的创新精神。以下通过几个实验简单展示其在大数定律教学中的应用。

3.1 频率稳定性的数学实验

伯努利大数定律从理论上证明了频率具有稳定性，且依概率收敛于随机变量的概率值，是蒙特卡罗法的理论基础。辛钦大数定律为随机变量数学期望的计算提供了实际可行的途径——随机变量的算术平均值趋向于其数学期望，是参数估计的理论基础。

抛硬币试验是典型的n重伯努利试验，是概率教学的经典实例，利用Python的matplotlib绘图库可以实现掷硬币的动态演示过程，横轴代表硬币出现正反面的情况，纵轴表示出现次数，利用变量作为标题还能动态显示正面出现的概率。图1显示了程序运行结果动画的部分截图，可以看出抛掷硬币次数与正面出现频率的动态变化过程，随着试验次数的增加逐步体现出频率稳定性的结论。

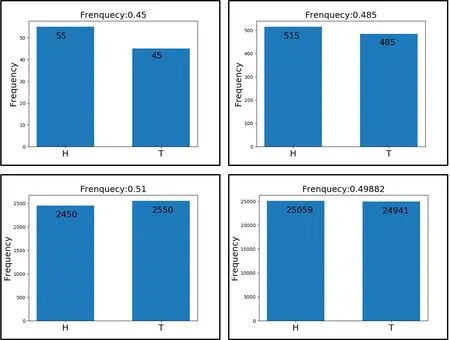
图1 频率稳定性动画截图

3.2 伯努利大数定律的数学实验

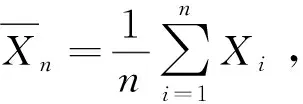
计算随机样本均值的过程中，均值依概率收敛于概率，均值稳定性体现在随着试验次数增加均值逐步收敛，最终依概率1收敛于概率p。图2为动画过程的部分截图，可以看出随着n的增加，均值在概率p上下两侧的波动越来越小，以动画显示实验过程更加具有趣味性，能加深对理论知识的理解[7-8]。

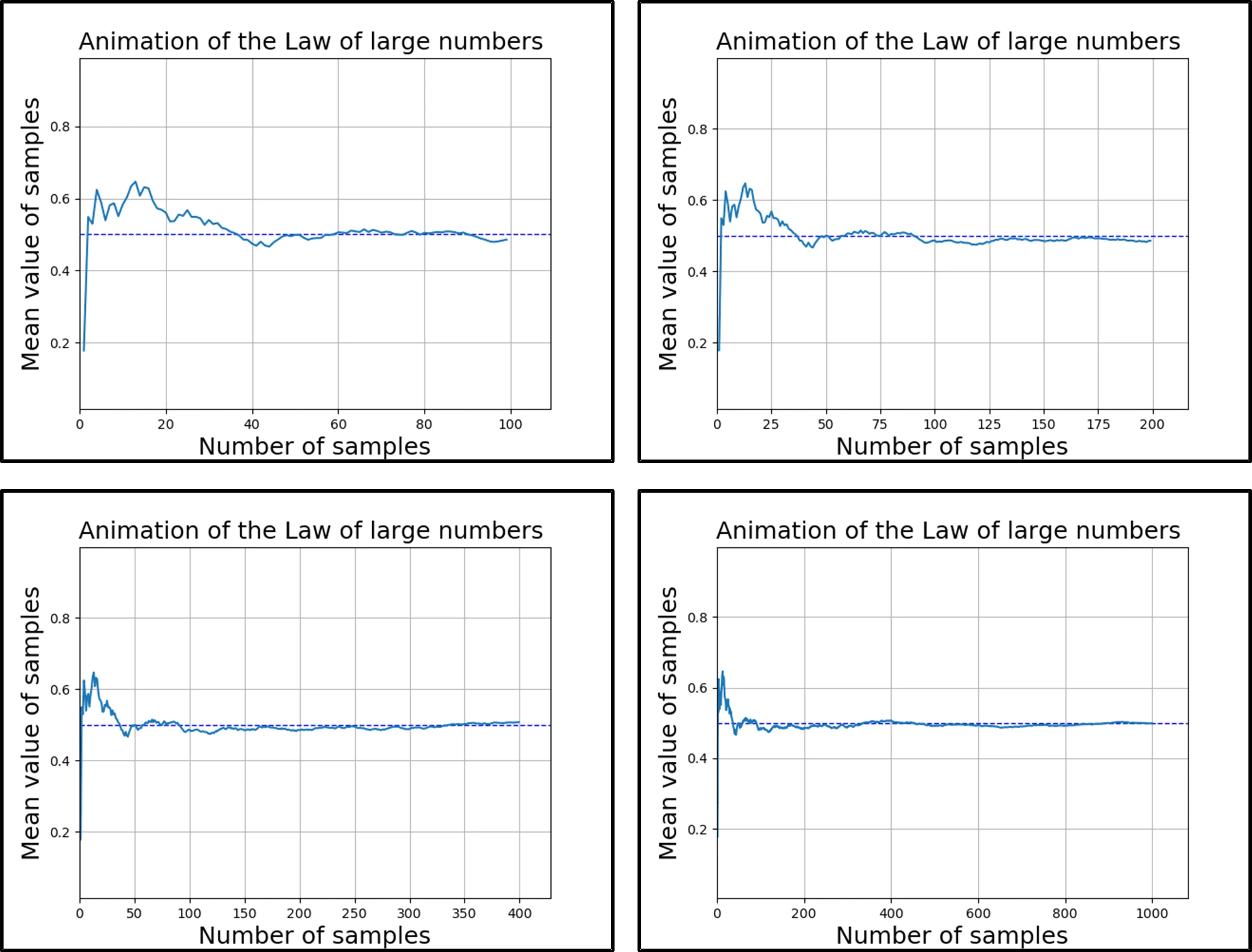
图2 大数定律均值稳定性动画截图

4 结语

数学实验丰富了学生认识数学定理的过程和方式，把感知、理解、运算和应用融为一体，图形更加直观，为学生揭示数学原理的本质和内在联系。丰富了教师的教学手段和教学内容，便于数形结合思想的运用，激发学生学习和应用的兴趣。

数学实验教学改变了教师和学生在教学活动中的关系和地位，教师不但是知识的提供者还是实验的指导者，学生变成主要的参与者，从单纯地接受知识变成自我学习、自我发现的主题，有利于教师因材施教，充分锻炼学生独立探索和解决问题的能力。

基于数学实验教学活动的开展发挥了理论联系实际的桥梁作用，利用软件进行数学理论的学习和训练，加大了教学信息量，使数学与计算机仿真有机结合起来，让学生能站在“科学研究”的角度进行数学理论的验证、再发现等创造性学习。数学实验能提高学生的动手、动脑能力，通过Python程序实验仿真，可实现和解决微积分问题中教学重难点的理解和应用，提高大学生学习数学理论的兴趣与用数学方法的技巧。