重复荷载下高延性混凝土加固受损混凝土无腹筋梁受弯性能试验研究

寇佳亮， 郑东东， 张浩博

(1. 西安理工大学 土木建筑工程学院， 西安 710048；2. 西安理工大学 省部共建西北旱区生态水利国家重点试验室, 西安 710048)

近年来，各种加固技术得到了广泛的发展，比如外加预应力加固法、增设支点加固法、粘贴纤维复合材料加固法。但对同样具有较好的物理力学性能而且施工容易，总体价格较低的HDC在加固混凝土构件上的应用，国内外缺乏系统的试验研究。

高延性混凝土是基于Li等[1]提出的高延性水泥基复合材料(engineered cementitious composites，ECC)，并改良了水泥基体的组成成分，抵抗周期荷载方面表现出良好的抗疲劳性能，在拉伸和弯曲作用下均表现出高延展性，具有典型的多裂缝开展和应变硬化特征，能显著改善混凝土材料的韧性和抗裂能力，在土木工程领域具有广阔的应用前景。用HDC进行加固的方法，秉承了其它众多加固法的优点，同时又发挥了其优良的材料特性，具有其它加固方法所不具有的很多优势。

目前，多数混凝土结构是在重复荷载下工作的，如桥梁，公共建筑物楼板，吊车梁等，因此这些混凝土结构极易在重复荷载的作用下内部产生损伤，造成强度降低，表面裂缝宽度加大，既影响建筑物美观，又造成一定的安全隐患，但拆除重建又花费巨大，造成经济浪费。因此寻找一种良好的加固材料来对原结构进行一定程度的加固显的尤为重要。高延性混凝土(high ductile concrete, HDC)是具有高强度、高延性、拉伸应变硬化特征的一种新型混凝土材料，其本身具有很高的抗拉强度和塑性变形能力，研究表明，HDC的抗拉强度是同等级混凝土抗拉强度的1.5倍，用HDC进行加固可以避免结构受拉区过早开裂，且可以增强钢筋与混凝土协同工作，进而影响结构的整体强度。因此，将HDC用于结构的加固设计中，研究其受力破坏的机理，为梁的加固设计提出一种新方法，具有理论意义和工程价值。

Esmaeeli等[2]采用ECC对砖砌体梁进行了加固，结果表明，ECC材料提高了构件的整体性，较薄面层的ECC也可提高构件的受弯承载力。Zhang等[3]将ECC包裹于普通混凝土梁表面，进行了疲劳试验研究，研究表明，ECC面层的钢筋混凝土梁表现出良好的性能，其承载力、延性普遍优于素混凝土面层的钢筋混凝土梁。Billington等[4]将PVA-ECC用于框架砌体填充墙的抹灰中，对PVA-ECC与墙黏结的端部进行了锚固，发现运用此种方法，拟静载试验结果显示，与未加固砌体填充墙相比，韧性提升了近10倍，破坏形式由传统框架砌体填充墙的脆性破坏变为延性破坏，大大提高了整个框架砌体结构的抗震性能。

在国内，张远淼等[5]采用ECC修复震损剪力墙，加固后试件的破坏模式表现出明显的延性，承载力基本得到恢复，且延性和耗能能力也显著提高。邓明科等[6]通过ECC面层加固砖墙的抗震性能试验发现，ECC面层能有效阻止裂缝的出现和发展，改善砖墙的脆性剪切破坏模式，提高试件的耐损伤能力，降低砌体结构的震后修复费用。徐世烺等[7]对钢筋混凝土梁采用超高韧性水泥基复合材料进行了加固，通过弯曲控裂试验研究表明增大了构件正常使用的极限荷载。

国内外学者在HDC加固方面已经进行了大量的研究，但多数集中在研究加固砌体结构以及加固构件的受剪及抗震性能，有关研究钢筋混凝土结构在重复荷载下受弯性能的文章却鲜有报道。因此本文着重研究了重复荷载作用下HDC加固受损混凝土无腹筋梁的受弯性能，课题组对10根HDC加固混凝土无腹筋梁进行了重复荷载下正截面受弯试验研究，分析了不同HDC加固厚度对受损梁承载力的影响程度，并推出了其极限受弯承载力的计算公式。

1 试验设计

1.1 试验原料

PVA纤维型号为日本KURARAYK-II纤维，其性能指标见表1。水泥：采用铜川某公司生产的P.O 42.5R普通硅酸盐水泥，其性能指标见表2。HDC试块：HDC试块与试验梁同期养护，其抗拉抗压性能指标见表3；减水剂采用聚羧酸系高效减水剂。

表1 PVA纤维各项性能指标Tab.1 Performance indexes of PVA fivers

表2 水泥的物理力学性能指标Tab.2 Physical and mechanical properties of cement

表3 HDC试块的抗压抗拉强度Tab.3 Tensile and Compressive strength of HDC test block

1.2 试验梁设计

本次试验共用10根无腹筋混凝土梁进行对比试验，其中原梁的截面尺寸b×h=100 mm×200 mm，试件长度为1 400 mm，混凝土设计强度等级为C20，强度保证率95%，设计塌落度为30～50 mm，混凝土配合比为水泥∶水∶砂∶石子=1∶0.65∶2.40∶3.92，保护层厚度20 mm，梁底纵向钢筋为2φ12，梁顶架立钢筋为2φ6，箍筋为φ6@75，原梁的配筋情况如图1所示。

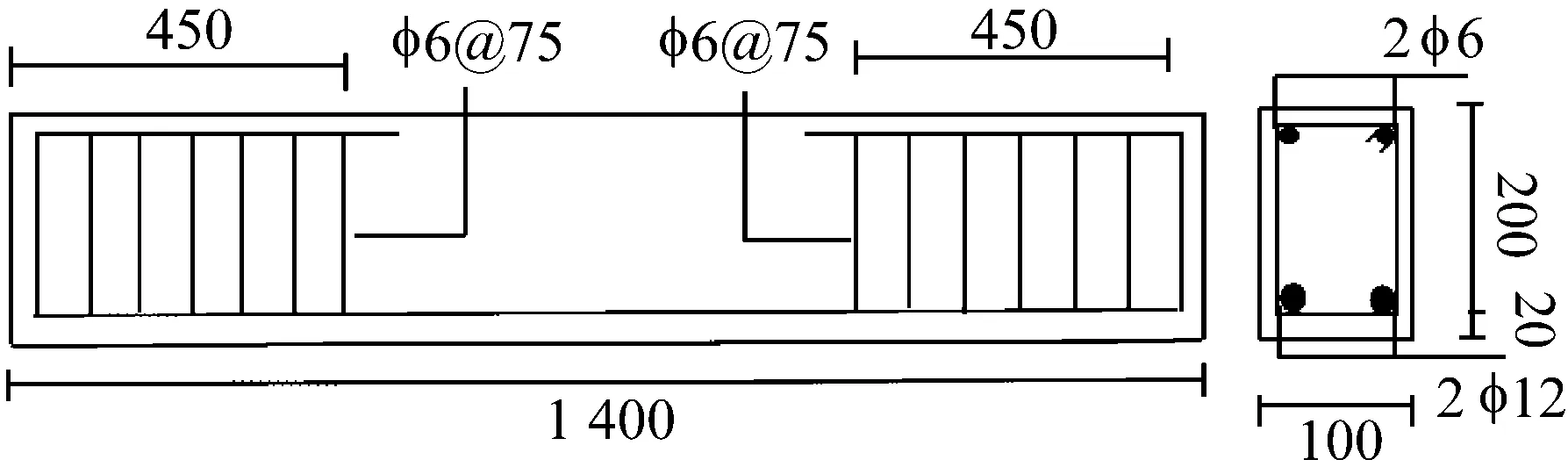
图1 试件截面尺寸及配筋图Fig.1 Section and reinforcement details of the specimen

本次HDC加固梁共分为4组10根足尺梁，所有梁均需凿掉原试验中被压坏部分，然后用HDC进行修补加厚。为保证试验结果准确可靠，每组梁都做不少于2根。A组梁为用HDC替补原梁毁坏部分的不加厚梁，数量为4根，分别编号(A-1)～(A-4)；B组为在用HDC修补基础上再用HDC加厚1 cm的梁，数量为2根，编号为B-1和B-2。C组与D组分别为在用HDC修补的基础上再加厚1.5 cm和2 cm的梁，数量均为2根，C组梁编号为C-1和C-2。D组梁编号为D-1和D-2。具体情况见表4。

表4 不同HDC加固厚度梁的数量Tab.4 Number of beams with different thickness strengthened by HDC

1.3 试验装置与加载制度

试验采用三分点加载。采用西安理工大学结构试验室的YAW-5000F液压伺服试验机，如图2所示。荷载通过分配梁作用在试验梁上，本文重复加载试验采用位移控制加载方式，加载速率为0.4 mm/min，一般建筑结构中梁的挠度限制值为L/250～L/300(L为跨度)，因此本次试验加载按每级增加4 mm(L/300)，每级循环3次。由于直接一次加载到位移为4 mm时，荷载较大，因此在1倍加载位移第一循环时用分级加载到4 mm，先加载到2 mm，然后观察裂缝发展情况。试验时根据电脑得出试件的竖向荷载，数据采集仪系统自动采集变形数据。同时在梁底部跨中及支座正对应下方设置千分表来测量梁的竖向挠度。加载制度如图3所示。

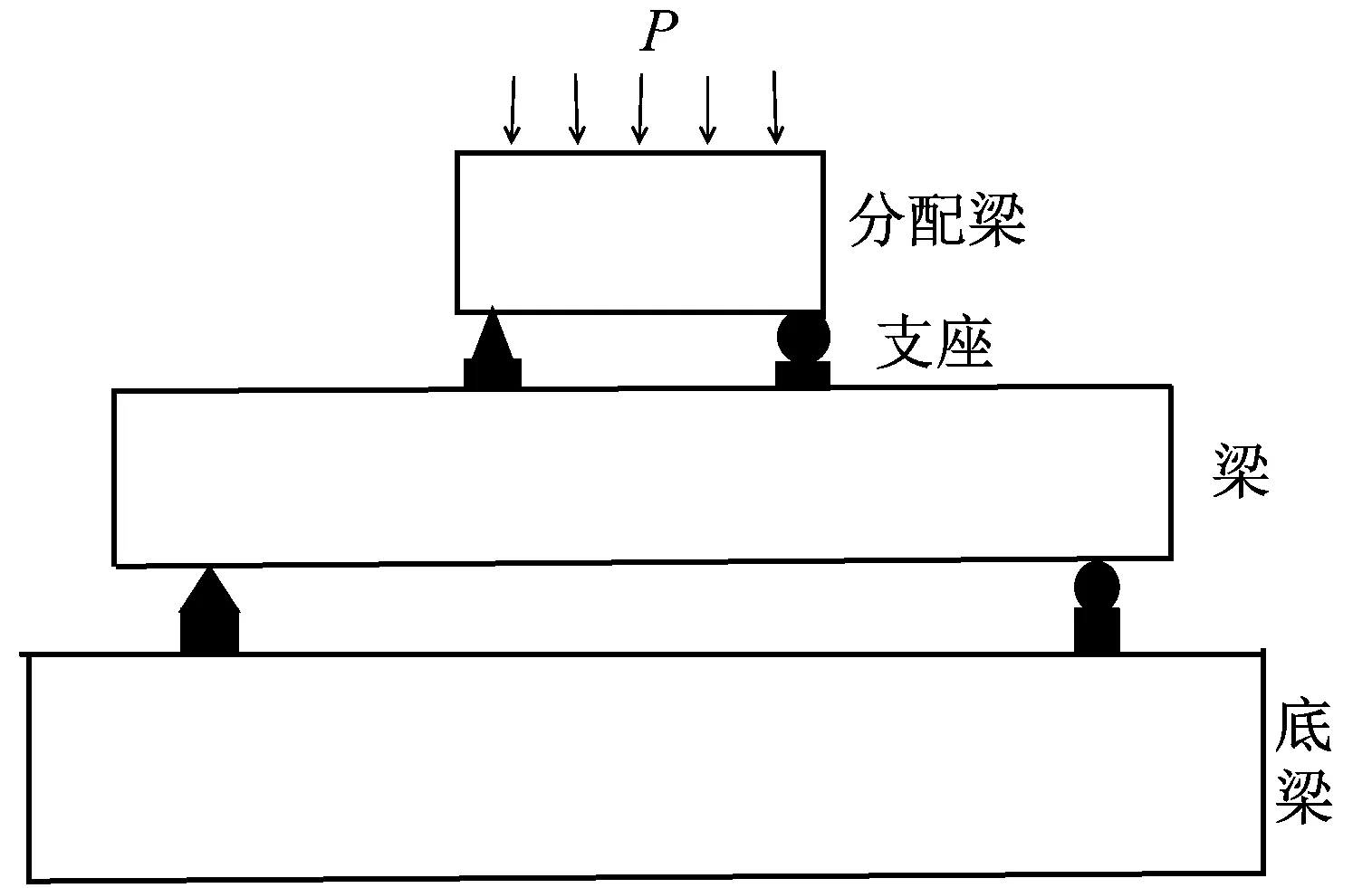
图2 试验加载装置Fig.2 Test loading device

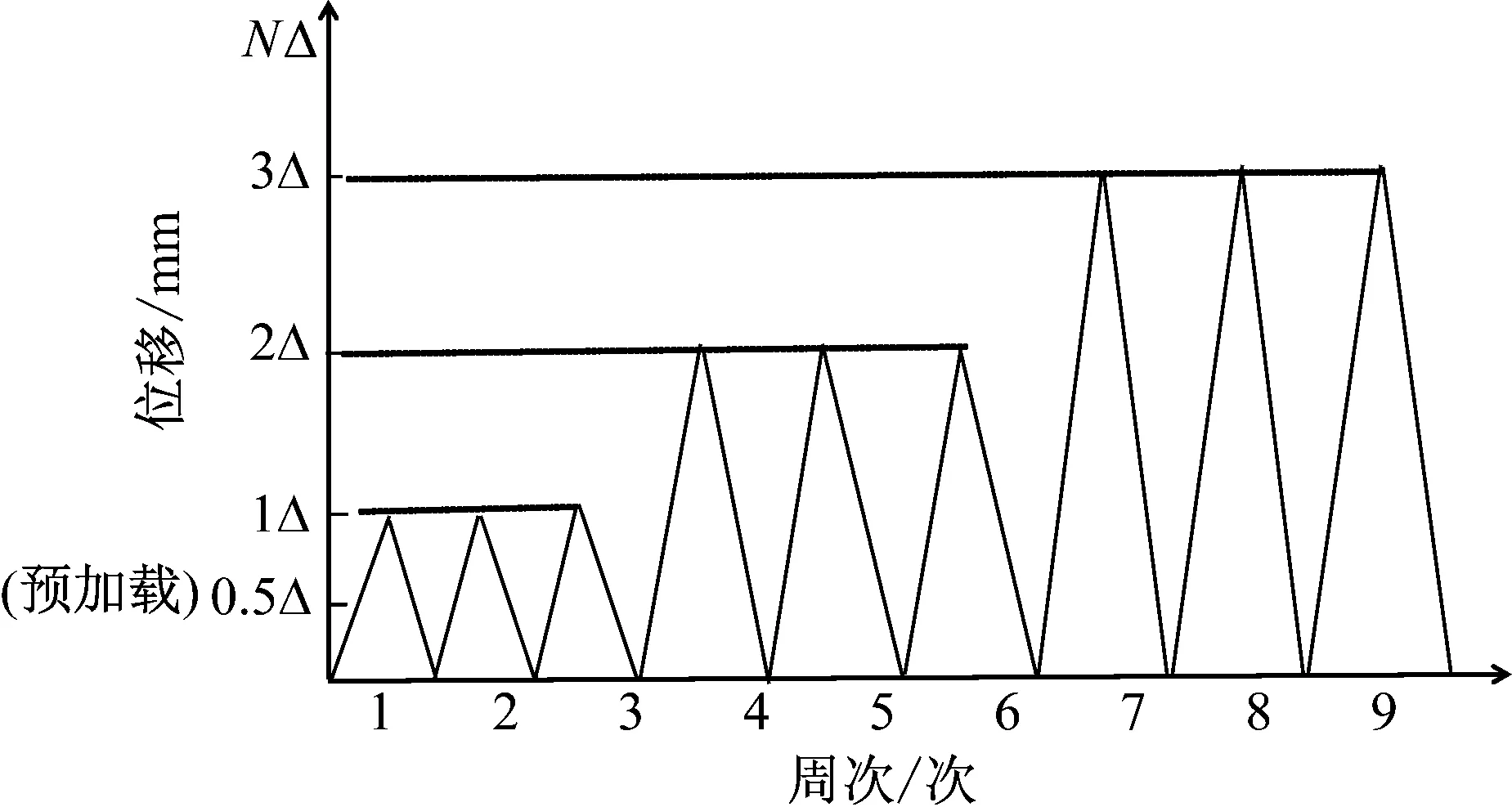
图3 加载制度Fig.3 Scheme of loading

2 HDC加固无腹筋梁的的受弯性能分析

2.1 加固前

梁在加固前当加载至24 kN时，在梁的左支座正下方梁底部出现5 cm长细裂缝。当加载至28 kN时，梁右支座正下方出现第二条裂缝，长约为4 cm。当加载至34 kN时，梁底部偏左方向产生11 cm斜向裂缝，当加载至42 kN时，梁跨中偏左、跨中正下方裂缝均向上延伸2～3 cm。加载至48 kN时，梁靠右侧底部产生19 cm细长裂缝。继续加载至75 kN时，梁右支座下方向左10 cm处产生8 cm竖直裂缝，随着荷载的继续增加，梁各处裂缝不断延伸扩展，当加载至60 kN时，梁底部左支座和右支座附近裂缝均斜向扩展4～5 cm，并且宽度明显加宽，大约1.5 mm。当加载至75 kN时，梁跨中以及偏右方向裂缝向上延伸了4 cm；当加载至95 kN时，梁顶部右支座附近产生9 cm斜向裂缝，直至加至120 kN，梁左支座正下方底部贯通，附近出现众多细小裂缝，伴随着撕裂的声音，梁最终被压坏。其它梁加载过程也经历上面几个阶段，除承载力以及裂缝发展略有不同外，其余基本一致。原梁破坏情况详如图4所示。

2.2 加固后

2.2.1 A组试验梁

梁A-2当荷载加至2 mm时，此时对应荷载为20.1kN，跨中底部出现5 cm长竖直微裂缝。当加载至1Δ(4mm)时，荷载达到39 kN，梁左支座，右支座附近出现10～13 cm竖直细长裂缝，在该位移下，对应荷载继续增长，分别达到了51.2 kN和69.4 kN，比该位移下第一次加载荷载分别提高了31.3%和78%，并在梁的底部出现细小竖直裂缝，但裂缝宽度无明显变化，说明此时加固梁正处于近似弹性工作阶段，荷载增长较快，裂缝几乎无发展。当加载至2Δ(8 mm)时，试验梁达到了极限承载力78.80 kN，比1Δ的峰值荷载增长12.4%，此时最大裂缝宽度为2.63 mm，裂缝发展迅速，因为此时荷载尚处于增长阶段，裂缝宽度适中，所以梁处于弹塑性工作阶段。在该位移下进行第二次以及第三次加载的过程中，极限承载力缓慢下降，分别为78.0 kN，75.49 kN，比该位移下的第一次加载荷载分别下降1%和4.2%，此时裂缝宽度在不断加大，第二次加载中最大裂缝宽度达到3.45 mm，第三次加载达到4.08 mm，相比于该位移下第一次加载时裂缝宽度分别增长31.2%和55.1%，说明当加载进入2Δ时，加固梁承载能力基本无变化，但裂缝宽度迅速增长，变形加大，判断此时加固梁进入屈服阶段。当位移加载至3Δ时，峰值荷载在达到73.51 kN后，比加固梁的极限承载力下降6.7%，此时的裂缝宽度已达到4.97 mm，比2Δ阶段的裂缝宽度增长89%，说明此时加固梁已经不能继续有效的承受荷载，梁进入破坏阶段，最后HDC加固梁被拉断。A组其他加固梁加载过程也经历上面四个阶段，除极限承载力以及裂缝发展略有不同外，其余基本一致。

2.2.2 B组试验梁

当加载至2 mm时，在梁B-2的左端底部出现10 cm细长裂缝，此时的裂缝宽度为0.23 mm。相应荷载为31.2 kN。当位移加载至1Δ时，对应荷载增加至47.2 kN，裂缝宽度为0.43 mm，荷载增长51.3%，裂缝宽度增长87%，但裂缝尚处于发展初期。在第二次以及第三次加载中峰值荷载缓慢增长，分别达到了63.5 kN和78.6 kN，比第一次加载荷载分别增长34.5%和66.5%。裂缝宽度扩宽至1.12 mm，此时加固梁荷载增长较快，裂缝宽度适中，加固梁处于近似弹性工作阶段。当加载至2Δ时，峰值荷载达到84.8 kN，此时最大裂缝宽度增大至2.84 mm，荷载比1Δ时增长7.9%，裂缝宽度增长154%，裂缝有斜向和竖直向上延伸的趋势，并且在该位移下第二以及第三次加载过程中，试验梁的峰值荷载达到了极限承载力，为88.90 kN，较1Δ时荷载增长13.1%，此时梁右侧底部产生平行裂缝，并伴随众多细小裂缝出现，裂缝的最大宽度为5.88 mm，此时裂缝已经发展迅速，但荷载增长放缓，此时加固梁进入弹塑性工作阶段，但加固梁以变形为主。当加载至3Δ时，峰值荷载下降至77.44 kN，较加固梁的极限荷载下降12.9%，此后承载力极速下降，裂缝持续变宽，加固梁破坏。梁B-1在加载各阶段的发展规律与梁B-1相近，体现了该加固厚度下梁发展的规律性。

2.2.3 C组试验梁

当加载至2 mm时，此时梁C-1比较稳定，梁表面均无肉眼可见的裂缝出现，此时的荷载为36.2 kN。当位移达到1Δ时，峰值荷载达到52.9 kN，比2 mm时荷载增长46.1%，说明此时加固梁正处于发展初期。在第二次以及第三次循环加载过程中，峰值荷载的增长缓慢，分别为83.2 kN和87.4 kN，比起第一次加载荷载分别增长57.3%和65.2%，且在梁的左侧产生三条新的斜向裂缝，但裂缝宽度发展不明显，此时加固梁处于近似弹性工作阶段，荷载增长较快，裂缝宽度无明显发展。当加载至2Δ时，承载力出现较大增长，峰值荷载达到91.3 kN，裂缝宽度也经历较大发展，出现了2.10 mm宽裂缝，此时荷载比1Δ第一次加载增长72.6%，裂缝宽度也出现了较大增长，梁处于弹塑性工作阶段。在该位移下的第二次加载下，峰值荷载增至94.5 kN，裂缝宽度发展至4.78 mm，且该裂缝底部发生贯穿。在该位移的第三次加载下，峰值荷载达到极限承载力，为99.26 kN。裂缝宽度扩展至6.42 mm，比起该位移下第一次加载，荷载分别增长3.5%和8.7%，荷载增长放缓但裂缝宽度比第一次加载增长128%和206%，说明此时加固梁在荷载变化不大的情况下裂缝充分发展，变形迅速加大，加固梁处于屈服阶段。此后在3Δ的加载过程中承载力极速下降，伴随着纤维撕裂的声音，加固梁破坏。梁C-2极限荷载和残余变形比梁C-1略小，但发展规律和梁C-1一样，在1Δ时处于弹性阶段，当加载至2Δ后期，梁即进入屈服阶段，继续加载，梁即告破坏。

2.2.4 D组试验梁

梁D-1在位移加载到2 mm时，梁跨中偏左部分出现第一条细长裂缝，长约10 cm，此时荷载为39.4 kN。当加载至1Δ时，在距离梁右端35 cm处，产生新的细长裂缝，长约14 cm，右支座底部产生15 cm长斜裂缝，此时的峰值荷载达到69.2 kN，相较于2 mm时承载力提高了75.6%。在该位移下的第二次以及第三次循环加载下，峰值荷载继续增长，分别达到93.5 kN和98.4 kN，较第一次加载的峰值荷载分别增长35%和42.3%，承载力增长仍处于比较稳定的阶段，且在加载过程中，距梁右支座8 cm处裂缝底部贯穿，同时跨中区段产生新的裂缝，但裂缝宽度无明显变化，此时梁处于近似弹性阶段。当加载至2Δ时，峰值荷载达到102 kN，比1Δ荷载增长3.7%。此时裂缝宽度急剧增加，由34.5 kN的0.74 mm增加到99.5 kN的5.62 mm。在第二次加载中，峰值荷载达到极限承载力106.5 kN，比1Δ时荷载增长8.2%，并在梁的顶部以及跨中底部产生新的裂缝，此时的裂缝宽度最大宽至7 mm，说明当加载至2Δ时，加固梁荷载增长明显放缓，但裂缝宽度却急剧开展，变形持续快速变大，梁进入屈服阶段。后续在梁的3Δ加载过程中试验梁承载力急剧下降，梁破坏。梁D-2破坏阶段和梁D-1保持一致，即在1Δ时处于稳定阶段，当加载至2Δ时进入屈服阶段。

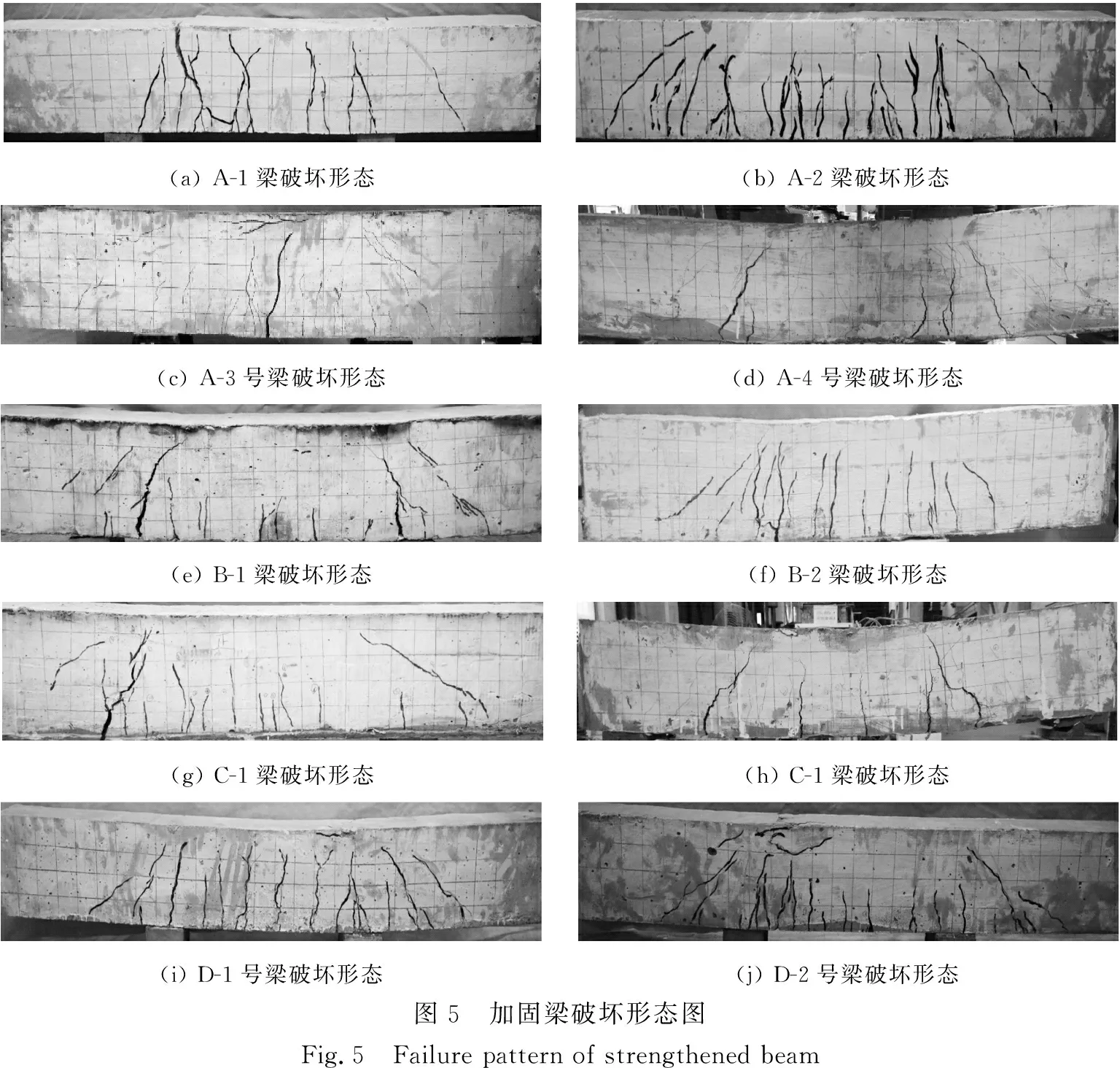
HDC加固梁破坏如图5所示。

2.3 加固前后破坏现象对比

对比梁加固前后的试验现象可知，梁在加固前，当加载到20～30 kN时，梁的左右两端即产生细长裂缝，当加载到40 kN左右时，梁的跨中底部开始出现细小裂缝，当加载至破坏荷载时，梁的跨中底部裂缝会突然出现贯通现象，前期无明显征兆，显示出明显的脆性破坏的特点。从图4可以看出，加固前梁的裂缝宽度变化较小，列缝数量较少，多集中于梁两侧的弯剪区，梁的破坏模式多属于斜拉、斜压破坏。梁加固后当加载至40～50 kN时，在梁的左右两侧开始出现细小裂缝，当加载至70～80 kN时，加载点附近出现密集的斜向裂缝，到加载后期，荷载增长缓慢，梁左右两侧及跨中底部产生贯通裂缝，梁顶部及梁底部均产生较大变形，裂缝宽度变宽，此时宽度可达3～4 mm，且从图5可以看出，裂缝分布密集且比较均匀；继续加载，试验梁承载力开始缓慢下降，梁在破坏过程中，变形不断增大，主裂缝不断变宽，最宽可达6～7 mm，但梁始终具有较高的承载力。加固梁破坏多属于弯曲，弯剪破坏。

与未加固梁相比，加固梁开裂荷载明显提高。从加固前后梁的图片对比来看，加固梁破坏时裂缝分布比较均匀，且裂缝数量明显增多。加固梁在底部贯通的情况下仍能承受较大荷载，后期剩余承载力较大，改善了原梁加载过程中瞬时破坏、裂缝较少、裂缝宽度不明显且裂缝分布不均匀的现象。

2.4 荷载位移曲线

重复荷载作用下试验梁的荷载-位移变化曲线可以反映重复加载过程中荷载与位移之间的关系，而且可以综合描述重复荷载作用下梁的承载力、延性、残余变形等性能指标，是研究梁综合受弯性能的重要手段。根据试验过程中采集到的荷载值和跨中位移绘制的重复荷载作用下各试验梁的滞回曲线如图6所示。

对HDC加固混凝土无腹筋梁来说，加固厚度越厚，加卸载下的荷载位移曲线越饱满，滞回曲线包围的面积越大。

(1) 由图6中可以看出，这种加固梁一般加载循环六次即告破坏，这是因为试验梁是在原梁钢筋屈服且梁身部分损坏的情况下加固的，故梁所能承受的加卸载次数主要由加固的HDC来提供，由于本试验在加固厚度这一变量上控制比较均匀，分别是0,1 mm，1.5 mm,2 mm,相差不大，导致不同加固厚度梁破坏时的加卸载次数以及残余变形的大小相差不大，虽然随着加固厚度的增长，残余变形略有减小，但都维持在4～5 mm范围内。

(2) 由图6中可以看出随着加固厚度的增大，试验梁承载力在不断提高，梁D-1比梁A-1承载力提高了40.6%，说明HDC加固厚度增加对提高梁的承载力比较明显。但随着加固厚度的增加，加固梁的加卸载次数却显示出下降趋势，由A,B，C组的6次到D组的5次，通过本次试验分析是由于随着加固厚度增加，试验梁的刚度也随之增加，承载能力不断提高，因而在每级加载位移下，D组梁都比前三组梁承受更大的荷载，造成D组梁内部更早的损坏，加卸载次数由此降低，说明受力幅度是影响疲劳寿命的关键因素;第二个原因是由于尺寸效应的影响，加固厚度越大，试验梁截面尺寸越大，内部存在缺陷的概率就越大，也就越容易加载破坏。且从图6中可以看出，随着加载次数的增加，试验梁由于加载过程中的损伤累积出现峰值荷载下降现象，特别是在加载后期，预示着梁开始破坏。加载后期在变形急剧增大的情况下梁仍能承受一定的荷载，A组加固梁在达到最大变形时所能承受的荷载均值为59.95 kN,占A组梁峰值荷载的76%；B组加固梁在达到最大变形时所能承受的荷载均值为75.2 kN,占B组梁峰值荷载的83.9%，说明HDC加固梁在承载力下降较小的情况下具有良好的变性能力，即具有良好的延性。用HDC加固可以有效改善钢筋混凝土梁脆性破坏的缺陷。在C组和D组梁加载过程中，当加固梁被加载至破坏并且钢筋外露的情况下，加固梁的承载力并没有明显的下降，说明HDC加固层越厚，梁的承载力会越高，而且加载到后期梁的承载能力越不容易下降。

2.5 残余变形

根据千分表采集数据的对比可以得到梁开裂时的开裂荷载以及所对应的变形、峰值荷载以及所对应的变形、最大变形以及所对应的荷载；分别如表5、表6、表7所示，同时得到了加载次数下荷载由最初加载到卸载至零时试验梁残余变形的大小，如表8所示，以及绘制出了不同加载次数下的试验梁残余变形图如图7所示。

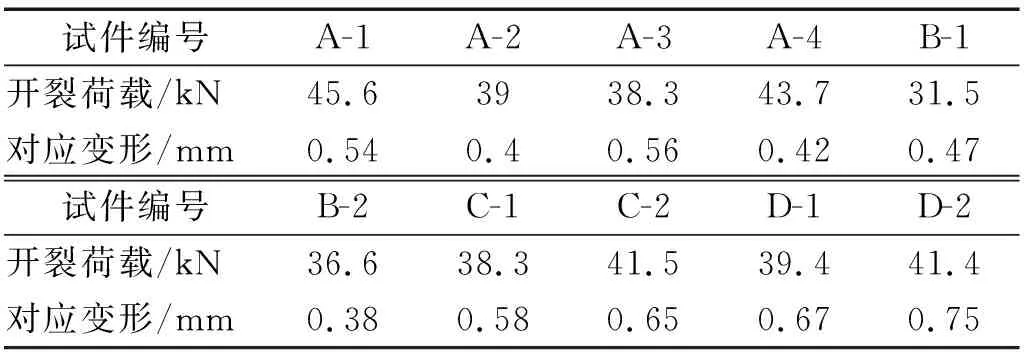
表5 开裂荷载及所对应的变形Tab.5 Cracking load and corresponding deformation

从表5可以看出，不同HDC加固厚度梁的开裂荷载相差不大，基本都在40 kN左右，这说明了不同HDC加固厚度对梁的开裂荷载无明显影响。

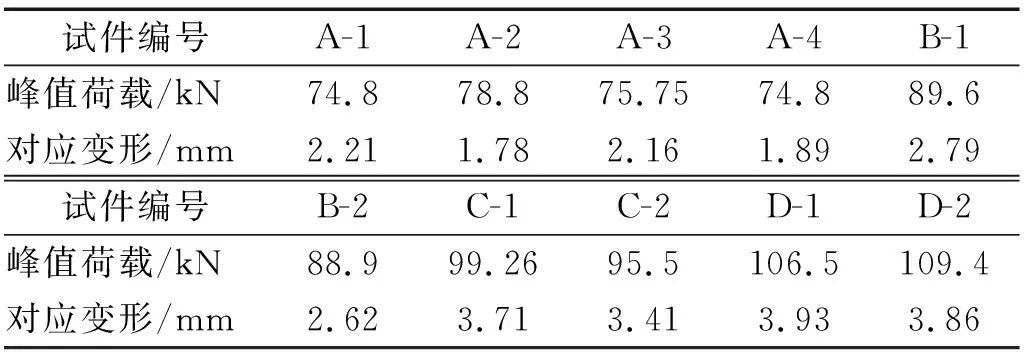
表6 峰值荷载及所对应的变形Tab.6 Peak load and corresponding deformation

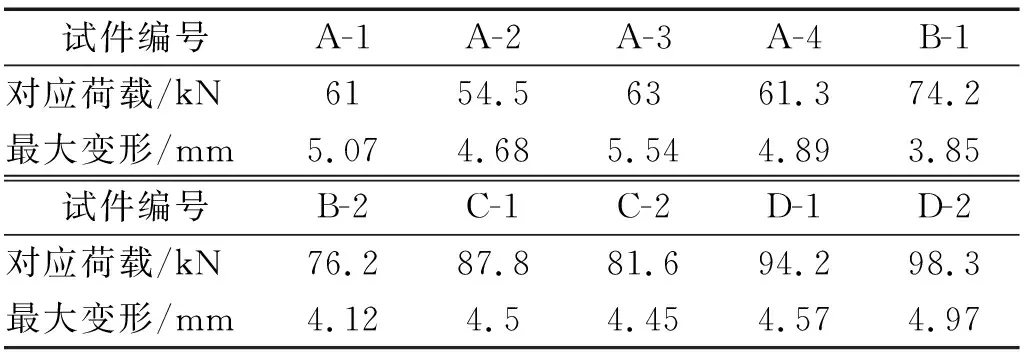
表7 最大变形以及所对应的荷载Tab.7 Maximum load and corresponding deformation

从表6可以看出，随着HDC加固厚度的增加，加固梁的峰值荷载不断提高，由A组梁的76 kN,B组梁的89.25 kN，C组梁的97.38 kN,到D组梁的107.95 kN；峰值荷载所对应的变形也在不断增长，由A组梁的2.01 mm，B组梁的2.70 mm,C组梁的3.56 mm到D组梁的3.9 mm,呈现缓慢的上升。

从表7可以看出，不同HDC加固厚度梁的最大变形基本相同，没有随加固厚度的增加表现出明显的变化规律，最大变形的较小值为3.85 mm，最大值为5.54 mm，相差不大，但最大变形所对应的荷载随着HDC加固厚度的增加不断增大，分别由A组的59.95 kN，B组的75.2 kN，C组的84.7 kN到D组的96.25 kN，所对应的荷载不断上升。

由图7可以看出试验梁的残余变形值随着加载次数的增加而增加，在第1次加载时，所有试验梁的残余变形值都很小，都维持在0～0.7 mm，并且加固梁的残余变形均值由A组的0.63 mm、B组的0.65 mm、C组的0.57 mm到D组的0.54 mm，即随着加固厚度的增加梁的残余变形有缓慢下降趋势。随着加载次数的增多，加固梁的残余变形值均随着加固厚度增加而减少。当试验梁加载至破坏时，试验梁的残余变形均值由不加厚的(A组)5.3 mm，加厚1 cm(B组)的4.825 mm，加厚1.5 cm(C组)的4.59 mm，到加厚2 cm(D组)的4.215 mm；残余变形均值最大减少20.47%；同一种加固厚度梁，随着加载次数的增多，残余变形值有明显的上升，HDC加固厚度为1 cm的梁，第一次加载的残余变形均值为0.65 mm，第二次加载时的残余变形均值增加到1.29 mm，比前一次增加0.64 mm，第三次加载的残余变形均值比前一次增加0.425 m,增长32.9%；第四次加载的残余变形均值比前一次增加1.01 mm，增长58.9%；第五次加载的残余变形均值比前一次增加0.695 mm，增长25.5%；第六次加载的残余变形均值比前一次增加1.4 mm，增长40.9%；且加载到后期，残余变形值的增长斜率要明显大于加载前期，说明试验梁随着加载次数的增多损伤不断累积，裂缝宽度与长度的不断扩展导致试验梁刚度与稳定性的下降，变形逐渐加快，直到最后破坏。

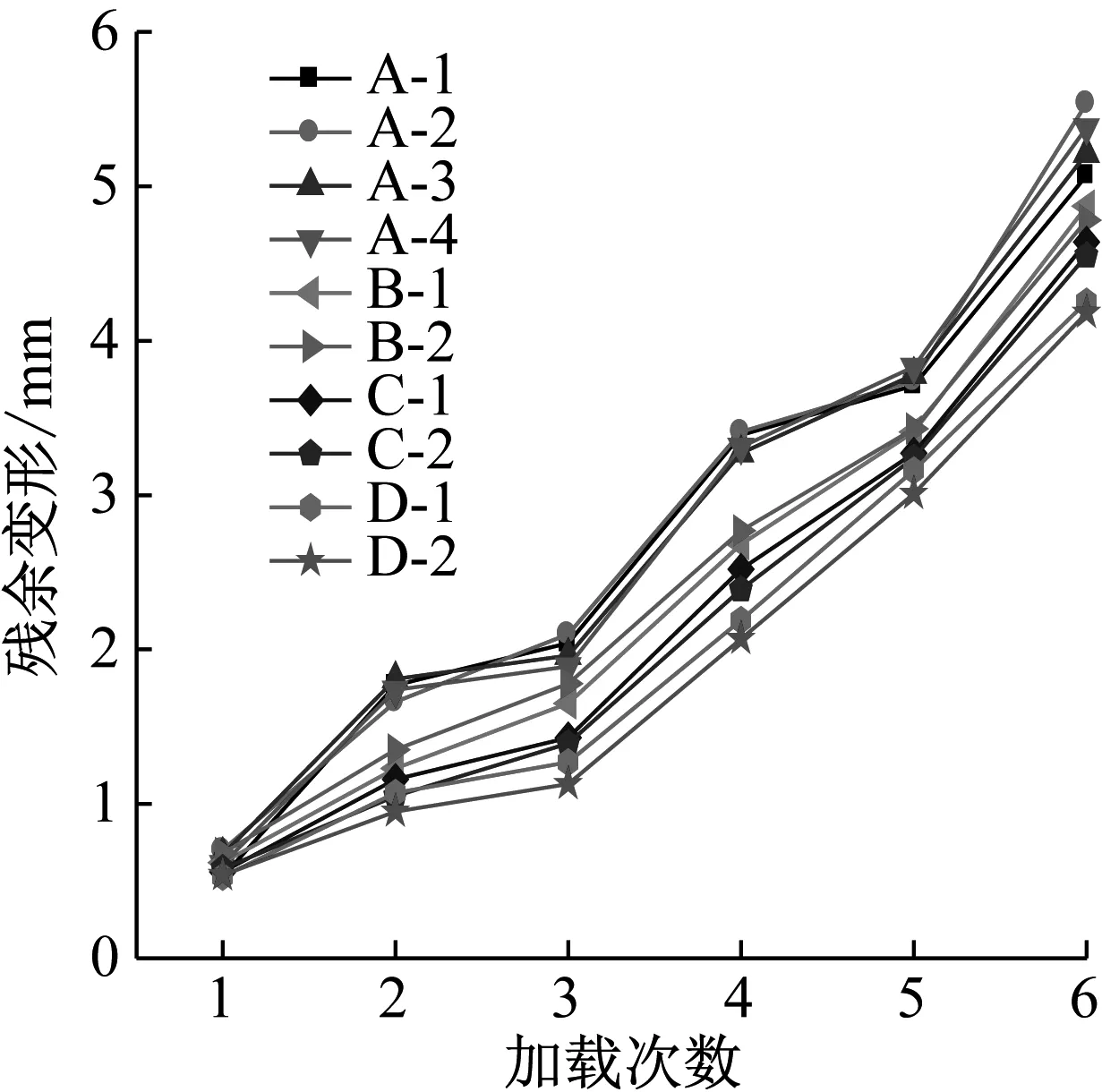
图7 残余变形比较Fig.7 Comparison of residual deformation

由表8可知，在梁正常加载过程中，不同HDC加固厚度梁最大残余变形值基本维持在3～3.8 mm，到梁最终破坏时，各加固厚度梁的残余变形值突然增大，但基本维持在4～5 mm范围内。其中加固厚度越大，其残余变形值越小。HDC加固层厚度为2 cm的梁残余变形平均值为4.215 mm，不加厚梁的残余变形平均值为5.3 mm，残余变形值增长25.7%，分析原因是由于由于当加固厚度越大时，试验梁的整体刚度就越大，抵抗受力变形的能力就越强，并且随着梁表面HDC层厚度的增加，HDC加固层参与梁整体受力的效果会愈加明显，由于HDC良好的韧性以及较高的耐损伤能力，会显著改善梁整体抵抗变形以及在荷载下容易开裂破坏的性能。

由表8数据可以看出，同一类型加固梁在相同加载次数下，梁的残余变形值都基本相似，相差不大。不同类型梁的对比中可以发现，在不同加载次数下，不加厚梁的残余变形值、加厚1 cm梁的残余变形值以及加厚2 cm梁的残余变形值依次减小，加厚1.5 cm梁的残余变形值维持在加固厚度为1 cm和2 cm梁之间。

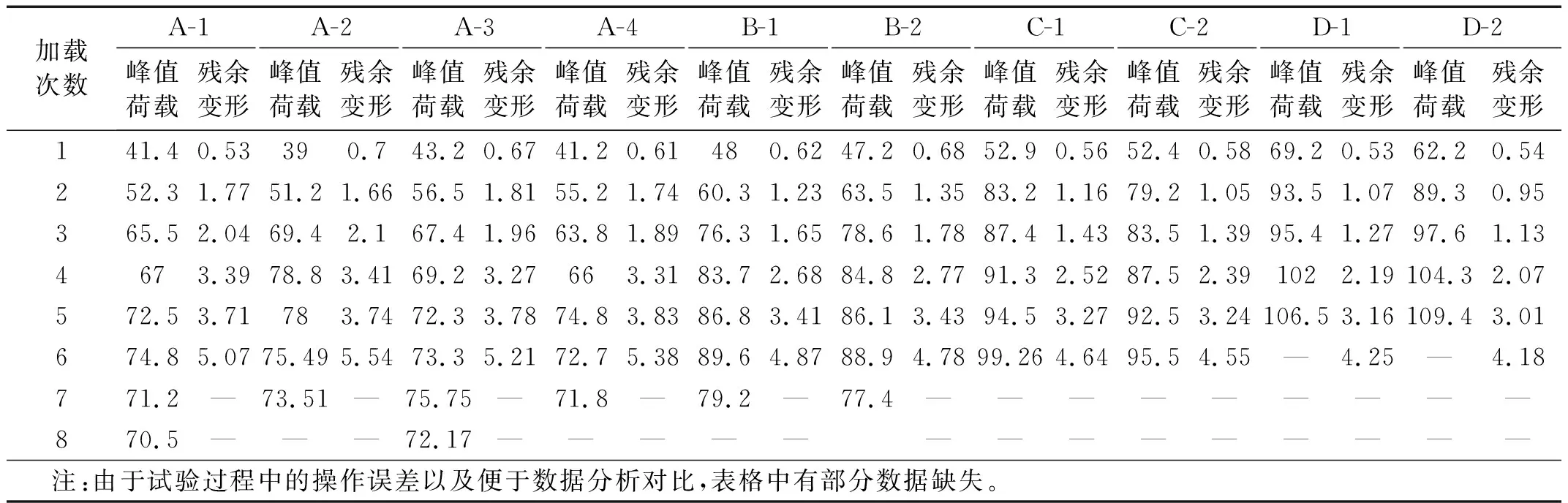
表8 试验梁各加载阶段峰值荷载以及所对应的残余变形Tab.8 Peak load and corresponding residual deformation of test beams in each loading stag

2.6 峰值荷载

通过试验室的数据采集系统，统计出了试验梁在不同加载次数下的峰值荷载，如表8所示，同时绘制出了不同加载次数下各试验梁的峰值荷载变化曲线图，如图8所示。对比试验梁各加载阶段的峰值荷载曲线可知：

(1) 随着试验梁加固厚度的增加，其极限荷载在不断上升。当加厚1 cm时，试验梁的极限荷载可达89.6 kN，当加厚1.5 cm时，极限荷载上升99.26 kN，当加厚至2cm时，极限荷载达109.4 kN，相对于不加厚梁来说，极限荷载可分别提高19.8%，32.7%和46.3%，可见加固厚度越大，对梁的极限承载力的提高越显著。

(2) 由图8可知，当加载次数较少时，加固梁的峰值荷载曲线斜率较大，说明此时试验梁承载能力强，梁的整体刚度大，梁比较稳定。随着加载次数的增多，到了加载后期随着裂缝的持续发展以及梁内部损伤的不断积累，峰值荷载曲线趋于平缓。相同加固厚度的梁随着加载次数的增加，峰值荷载的发展规律基本保持一致。不同加固厚度的梁，加固厚度越大，梁在不同加载次数下会出现更大的峰值荷载。且从图8中可以看出加固厚度为2 cm和1.5 cm的梁在第二次加载时，荷载上升开始减缓，而不加厚梁和加厚1 cm梁在加载到三次以后才开始出现荷载上升减缓的现象，说明了加固梁加固厚度越大，加载前期承受荷载能力越强。从图8中可以看出，随着加载次数增加，到了加载后期，加固梁在变形逐渐增大的情况下仍能承受较大荷载，说明了HDC具有较好的延性，用HDC进行加固可以较好地改善梁的脆性破坏的性质。

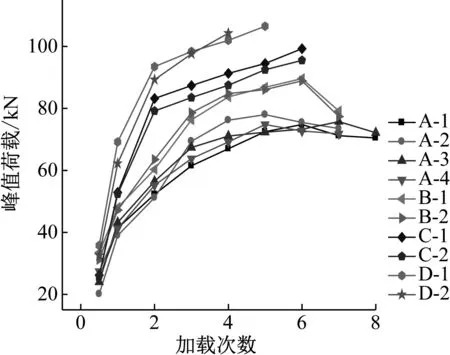
图8 各阶段峰值荷载Fig.8 Peak load at each stage

2.7 耗能能力

根据图6滞回曲线，可以计算出不同HDC加固层加固厚度下各加固梁的耗能能力大小，计算结果见表9。

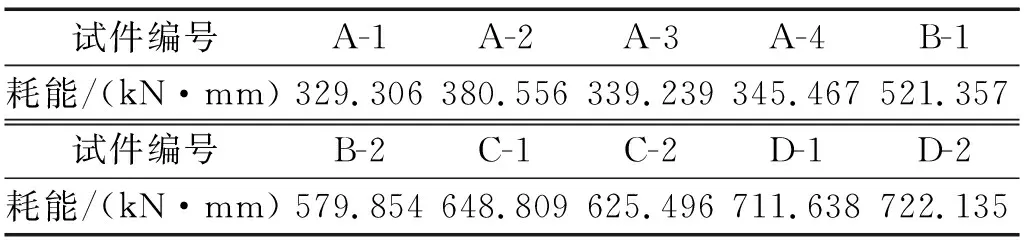
表9 试件累计耗能Tab.9 Energy dissipation of specimens

由表9可知，随着HDC加固层厚度的增加，加固梁耗能能力逐渐增强，当HDC加固层厚度为0时，加固梁的耗能基本维持在330 kN·mm附近，当HDC加固厚度增至1 cm时，加固梁耗能最大为579.854 kN·mm,比起加固厚度为0的梁的耗能平均值增长了66.3%。当HDC的加固厚度增至1.5 cm时，加固梁的最大耗能达到648.809 kN·mm，比起加固厚度为1 cm梁的耗能平均值，耗能增大17.8%，当HDC加固层厚度增至2 cm时，加固梁的最大耗能为722.135 kN·mm，比起加固层厚度为1.5 cm的加固梁耗能平均值增长13.3%，虽然HDC加固厚度越大，加固梁的耗能越大，但相邻两种加固梁的耗能差距会越来越小，随着加固厚度增加，耗能增长效果会逐渐降低。

3 加固梁的承载力分析

3.1 基本假定

GB 50367—2013《混凝土结构加固设计规范》[8]中指出采用增大截面法加固钢筋混凝土结构构件，其正截面受弯承载力应按现行国家规范GB 50010—2010《混凝土结构设计规范》[9]的基本假定进行计算：

(1) 增大截面加固梁新旧混凝土界面没有出现滑移，截面应变应符合平截面假定，即正截面应变按线性规律分布，指构件在荷载作用下，随着荷载的增加，截面钢筋和混凝土的应变沿截面高度方向直线变化。

(2) 混凝土加固受弯构件，其截面受拉区的拉力不考虑混凝土的抗拉作用，全部由钢筋承担；HDC加固梁需要考虑HDC的作用，由于HDC的极限拉应变高于钢筋的屈服应变，因此钢筋屈服之后，在变形协调作用下，HDC的拉应变还较小，受拉区HDC的作用不可忽略；经分析比较，采用Kanda等[10]HDC受拉本构模型，HDC受拉本构模型为

(1)

式中：σcr、εcr分别为出现第一条裂缝时HDC材料的应力、应变；σt0、εt0分别为峰值状态时HDC材料的应力、应变；E0为弹性阶段HDC构件的初始弹性模量。

(3) HDC受压本构模型采用Han等[11]提出的HDC受压本构模型，如下式所示

(2)

式中:σcp、εcp分别为峰值状态时HDC材料的应力应变；εcu为HDC材料的极限压应变。

(4) 纵向受拉钢筋的极限拉应变取0.01。

(5) 纵向钢筋的应力-应变关系采用理想弹塑性模型，其表达式为

(3)

式中：fy为钢筋的抗拉或抗压屈服强度；σs为对应于钢筋应变为εs时的钢筋应力值；εy为钢筋的屈服应变，即εy=fy/Es，Es为钢筋的弹性模量。

3.2 受弯承载力计算

3.2.1 加厚梁

根据基本假定，HDC加固梁和普通钢筋混凝土梁正截面承载力计算的基本假定相同。基于HDC加固受损混凝土梁试验结果，得出了不同加载厚度下试验梁简单实用的承载力计算公式，其中由于HDC具有优异的抗拉性能，因此梁的受拉区不能忽略HDC的抗拉承载力。假定截面受压区边缘HDC达到了其极限压应变εcu假定此时截面受压区高度为xc，则距截面中性轴距离为y的HDC纤维处的应变可按下式计算

(4)

钢筋的拉力及其距中和轴的距离ys可分别按下式计算

Ts=σs×As

(5)

ys=h0-xc

(6)

式中：h0为有效截面高度；假定此时截面受压区高度为xc受拉区HDC的拉力Tc可按下式计算：

Tc=σtbt

(7)

式中：b为截面宽度；t为HDC厚度

根据截面的平衡条件，可写出以下两个平衡方程

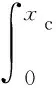
(8)

∑M=0

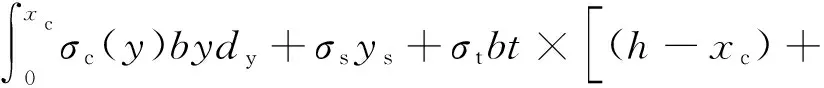
(9)

将HDC受压本构代入式(8)、式(9)，可求解截面承载力，然而由于受压区应力图形为曲线，计算相对较为复杂。为了简化计算，可对受压区应力图形进行等效，等效的基本原则为：

(1) 等效矩形应力图形的面积应等于曲线应力图形的面积，即HDC压应力合力C的大小相等；

(2) 等效矩形应力图形的形心位置应与曲线应力图形的形心位置相同，即压应力合力C的作用点位置yc不变为了推导等效矩形应力图形与曲线应力图形之间的关系，取等效矩形应力图形的高度为x=β1xc,等效应力为α1fc，《查混凝土结构设计原理》[12]可得表10，由表10可知本次β1取0.8，α1取1.0。

表10 混凝土受压区等效矩形应力图形系数Tab.10 Graphic coefficients of equivalent rectangular stress in compression zone of concrete

fc=0.88αc1αc2fcuk

(10)

FtHDC=ftHDC×bc×t

(11)

∑x=0

(12)

∑M=0

(13)

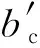
3.2.2 不加厚梁

当梁不加厚时，此时梁截面无加固层，但有HDC的修补部分，根据试验结果可知，修补部分约占梁截面面积的5%，考虑到HDC加固面积以及厚度较小，因此不加厚梁的承载力公式采用极限状态计算。不加厚梁的承载力公式为

(14)

(15)

其中α为考虑HDC混凝土受拉时对截面弯矩的影响系数，在此取1.25。

为了验证上述公式在计算HDC加固足尺构件抗弯承载力时的有效性，用本次试验的结果与计算结果进行了比较，比较结果如表11，其中Mcu为增大截面加固梁承载力计算值，Mtu为增大截面加固梁承载力试验值，Mcu/Mtu为计算值与试验值的对比，并对Mcu/Mtu的结果进行了平均值，标准差以及变异系数的计算，计算结果如表11所示。

表11 试件承载力计算值与试验值比较Tab.11 Comparison between calculated and experimental values of bearing capacity of specimens

由表11可知，计算值与试验值误差在一定范围内，推导出的HDC加固梁试件受弯承载力值与试验值差别不大，且标准差以及变异系数较低，说明本试验理论推导与试验结果较好吻合，数据离散程度低，且准确可靠，本文所推导的HDC加固梁受弯承载力计算公式可以较好地表示HDC加固梁的破坏规律。

4 结 论

通过对HDC加固梁在反复荷载下进行压弯试验，得出以下结论：

(1) 用HDC混凝土加固受损梁时，加固厚度越大，梁的极限承载力越高，且随着加固厚度的逐渐增大，极限承载力提高幅度越明显。

(2) 用HDC加固受损梁时，不同加固厚度梁的残余变形值相差不大，且随着加固厚度的增大，梁的残余变形有减小的趋势，当加固厚度达到2 cm时，加固梁的承受加卸载次数的能力会降低。

(3) 对于加固梁来说，加固厚度越厚，加卸载下的荷载-位移曲线越饱满，滞回曲线包围的面积越大，说明加固梁的耗能能力与加固厚度成正比。

(4) 在原梁混凝土被压坏，钢筋屈服的情况下，用HDC对受损梁的表面进行修补加厚，梁在裂缝开展，变形性能，承载力方面均有较好表现，说明用HDC加固受损梁是一种行之有效的加固方法。

(5) 根据加载试验得出的试验结果，以及通过将受压区曲线应力图形等效为矩形应力图形的方法，推导出了简单实用的不同HDC加固震损混凝土无腹筋梁在重复荷载下的极限承载公式，且计算值和试验值吻合较好。