回转式振动控制装置参数优化设计
徐 训, 陈 浩, 朱亚杉, 田克兢, 林廷灿
(武汉理工大学 土木工程与建筑学院, 武汉 430070)
主动质量阻尼器(active mass damper, AMD)因其减振效果好、控制力实时可调以及鲁棒性强等优点,在工程结构的振动控制中得到了广泛研究与应用[1-4]。主动控制算法直接影响着AMD的控制效果,许多学者在此方面做出了贡献。Yang[5]最先将现代控制理论引入到土木工程的振动控制中来。Chang等[6]利用LQR最优控制理论研究了ATMD的控制性能。Nishimura[7]提出了最优位移反馈的控制算法。还有一些如H∞最优控制[8],极点控制算法[9]也被学者应用到AMD的算法实现中来。
结构AMD控制系统的控制品质取决于AMD的系统参数和控制参数。因此,参数的选取也成为了值得研究的问题。祁皑等[10]采用估计的结构参数K和M选取权矩阵Q,并分析了AMD参数对控制效果的影响。王磊等[11]采用人工鱼群算法优化了AMD系统的权矩阵,验证了该方法对权参数选取的准确性和有效性。
然而基于上述研究的AMD采用的作动器大多为液压作动器或伺服电机作动器,前者构造复杂、占空间大、维护成本高,后者需要机械传动部件,响应慢等。欧进萍等[12]所提出的电磁驱动AMD系统虽能解决上述问题,但存在着质量块行程受限的问题。在大震或较大风荷载作用下,AMD行程很大,加上结构空间有限,质量块易与主体结构发生碰撞,破坏控制系统。因此为保证直线AMD安全稳定运行,通常需要在轨道两端增设限位装置来约束AMD行程 ,不仅给设计来带麻烦,还会限制AMD最优的控制效果。为此Zhang等[13]提出一种旋转激励的作动器,惯性质量通过轻杆连接电机做旋转运动,解决了电磁驱动直线AMD质量块的行程问题。
本文将“旋转”运动的概念,引入到直线电磁驱动的AMD装置,将直线轨道改进为旋转轨道,提出一种电磁驱动的回转式振动控制装置(RVCD)。不同于文献[13]的是,其驱动无需旋转电机带动,而是由电磁直接驱动。质量无需轻杆连接,这会解决轻杆的承重和所占空间的问题。轨道形式不局限于圆形,以适应不同条件下的控制。本文首先,建立了结构和RVCD耦合的数学模型,针对该系统的强耦合性和非线性,采用无量纲处理以及全局坐标变换将其简化为级联形式,并为其设计了滑模控制器;接着,通过仿真来验证RVCD控制系统的减振效果和鲁棒性,并对装置物理参数进行敏感性分析;最后,针对滑模控制算法中多参数的最优取值问题,本文从AMD做负功的角度构造了目标函数,提出了一种基于粒子群算法的优化方法。
1 RVCD模型及控制器设计
1.1 系统模型
RVCD的构造如图1所示,固定组件安装于被控结构,轨道组件安装在固定组件外表面,线圈绕组环绕在轨道外侧的定子铁芯上,质量块卡接于轨道,内部贴有永磁体,并通过滚珠在轨道内滑行。其驱动方式利用了同步电机的原理:定子线圈绕组通入三相正弦交流电后会产生旋转磁场,质量块内的永磁体会产生恒定磁场,由于磁极间的相互作用,定子的旋转磁场与永磁体的恒定磁场之间产生的磁拉力会拉动质量块旋转,并最终使质量块跟随旋转磁场同步旋转。质量块在旋转时会受到切向的惯性力和法向的向心力作用。这两个力的反作用力充当结构的控制力,从而控制结构的振动。

1. 固定组件; 2. 质量块; 3. 限位弹簧; 4. 挡板; 5. 线圈绕组; 6. 永磁体; 7. 定子铁芯; 8. 轨道组件; 9. 滚珠; 10. 连接螺栓图1 回转式振动控制装置构造图Fig.1 Construction of rotary vibration control device
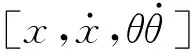
由拉格朗日方程可以得到其动力学模型

图2 回转式振动控制装置/结构耦合系统俯视图Fig.2 Top view of rotary vibration control device/structure coupled system
(1)
(2)
为便于控制器的设计,引入下列无量纲量[14]
(3)
(4)
(5)
(6)
式中:xd,fd,u,Cd表示无量纲化的结构位移,外界干扰,控制力矩和阻尼;τ表示无量纲化时间;ε是一个辅助参数,表示水平运动与旋转运动的耦合关系。
结构与RVCD耦合的数学模型(1)和(2)可写为
(7)
(8)
可以看出,系统(7)和(8)具有强耦合性,引入下列坐标变换[15]
(9)
系统(7)和(8)转化为下列级联规范形式
(10)
式中:
(11)
1.2 控制器设计
对于具有非线性项的系统(10)而言,其控制变量(η和ξ)数目大于输入数目(ν),是一个典型的欠驱动系统,本文采用滑模控制算法设计其控制器。
系统的控制目标是使状态变量达到平衡点,即
(12)
由式(9)可知,式(12)等价于
[η1η2ξ1ξ2]T=[0 0 0 0]T
(13)
取滑模函数为
s=c1η1+c2η2+c3ξ1+ξ2
(14)
其中,c1,c2,c3均大于0

(15)
采用指数趋近律,有
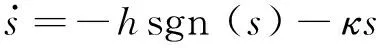
(16)
其中,h=h0+c2D,|fd|≤D,h0>0,κ>0
结合式(15)和式(16),可以求解出
ν=-c1η2-c2(-η1-Cdη2+εsinξ1+εCdξ2cosξ1)-c3ξ2-hsgn (s)-κs
(17)
定义Lyapunov函数为
(18)
则

κs2≤0
(19)
故系统的状态变量会渐进稳定到平衡点。
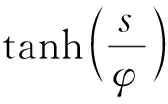
(20)
式中,φ>0,其大小决定了函数的拐点位置,双曲正切函数的稳定性可由同样方法证明。
2 PSO优化滑模控制参数
粒子群算法(particle swarm opimization,PSO)是一种常用的进化优化算法,其原理是:在解空间内随机生成一群粒子,计算每个粒子对应的初始适应度值(目标函数值),通过每一次迭代过程,粒子会更新自己的位置,从而获得新的适应度值,与初始的最优适应度值进行比较,直到找到全局的最优解。粒子的更新公式为
(21)
式中:k表示迭代次数;h1,h2表示学习因子;r1,r2是[0,1]内的随机数;V为粒子速度,P为个体极值;G为群体极值;X表示粒子当前位置。
AMD对结构的控制效果从本质上来讲,是通过主动控制力对结构做负功来抵消外界干扰输入到结构的能量实现的[17],故可从能量角度设定优化的目标函数。对式(1)各项同乘位移微分,在外界激励持时t内积分,可以得到RVCD-结构能量平衡方程
Ek+Es+Ed+Eu=Ei
(22)
其中:
(23)
(24)
(25)
(26)
(27)
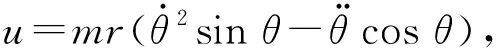
对于弹性结构,无塑性变形,其应变能等于弹性势能。在振动结束时系统的动能和弹性势能变为零,输入到结构的能量最终由自身阻尼耗能和RVCD所作功来承担,RVCD通过摩擦将负功转化为热能耗散掉。因此RVCD所做的负功越大,结构承担和消耗的能量就越小。
文献[18]指出,AMD控制力过大不仅无法取得更好的控制效果,还可能超出作动器的额定驱动力。本文的控制目标应为在保证结构控制效果的前提下适当降低作动器的出力,因此本文定义目标函数为
(28)
式中:Eie和Eue表示结构停止振动时外界干扰输入到结构的能量和RVCD所做的总功;Nmax和Ns表示RVCD的最大驱动力和额定驱动力;λ1和λ2是权系数,二者之和取为1。
在优化过程中,必须始终满足实际结构中AMD的约束条件,即
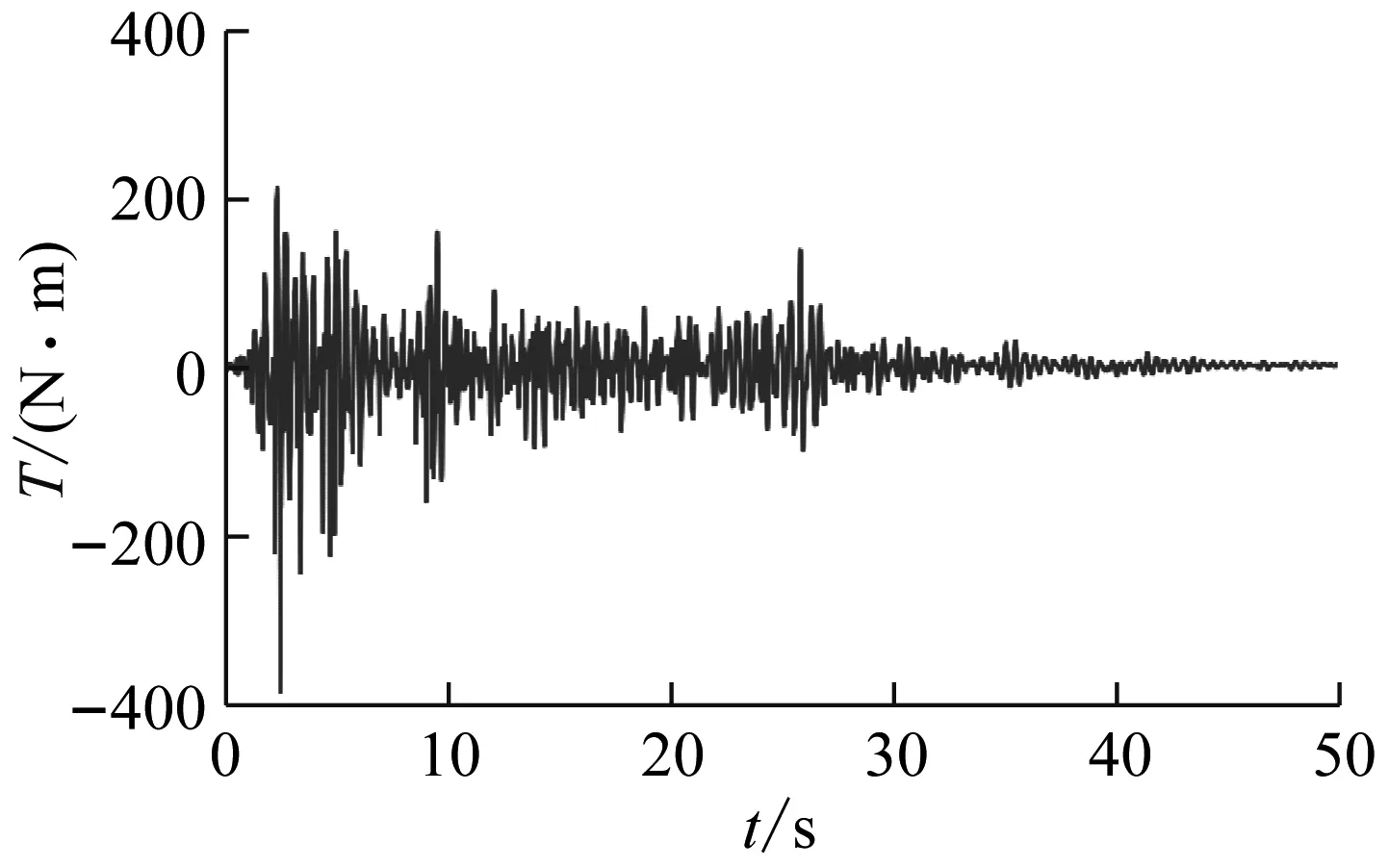
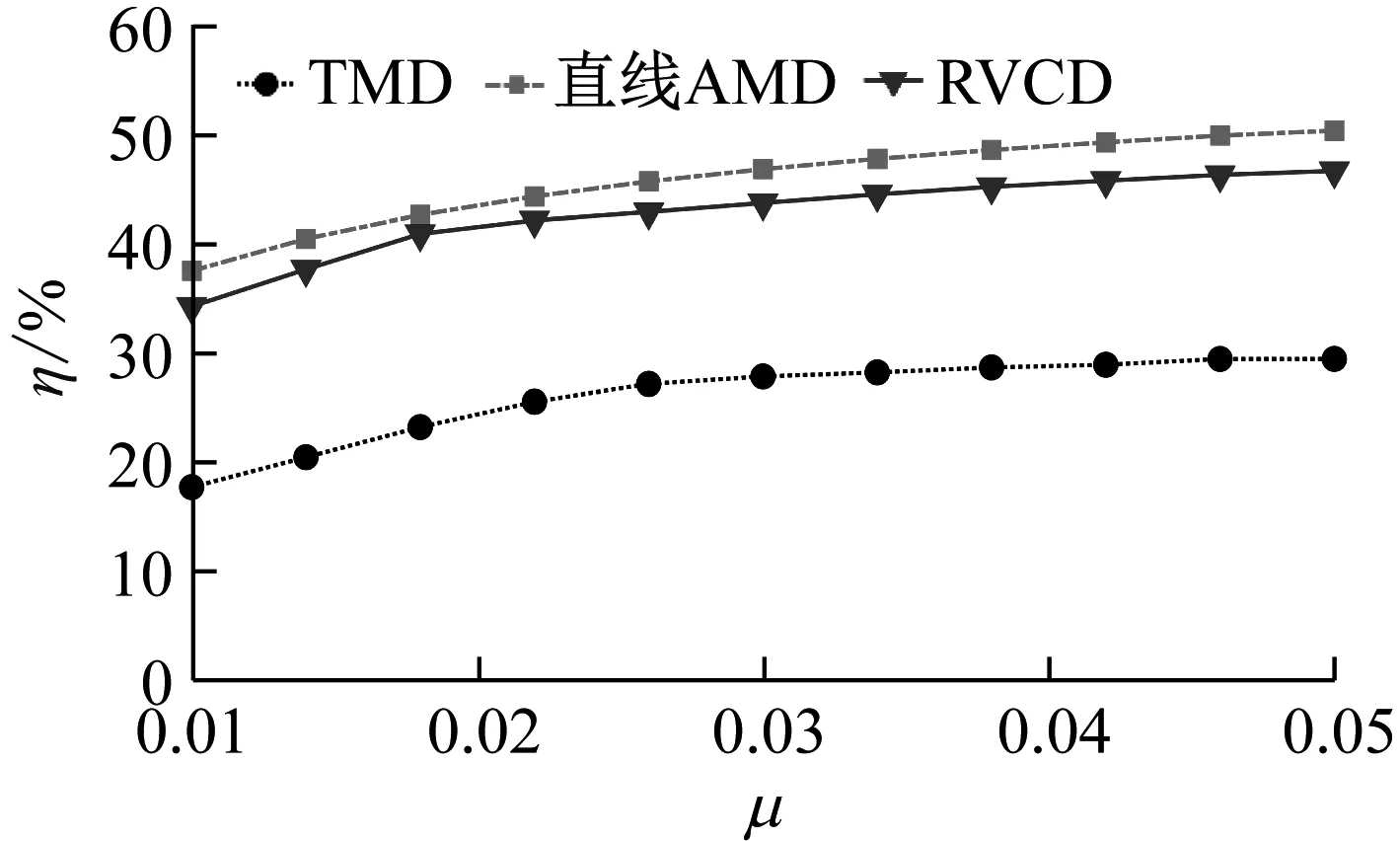
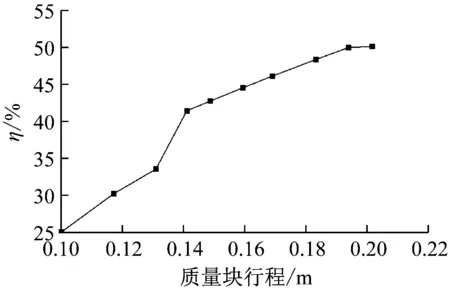
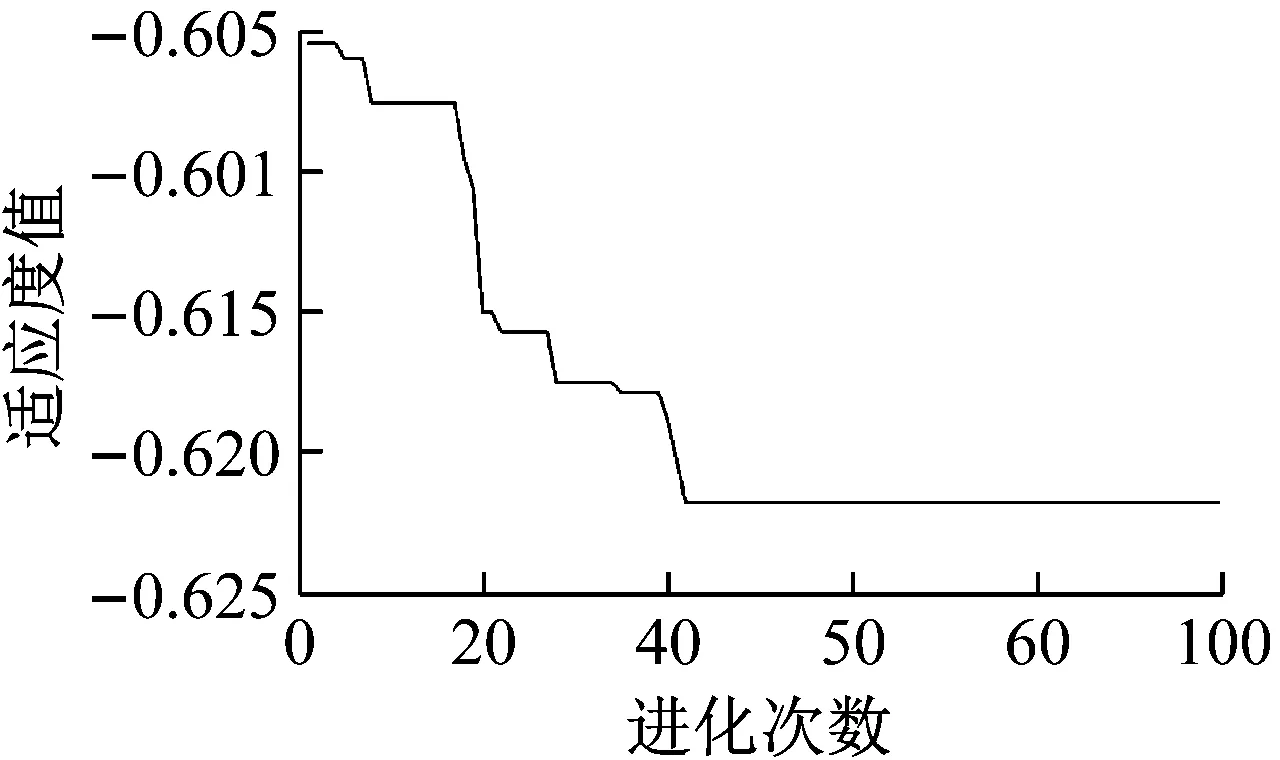
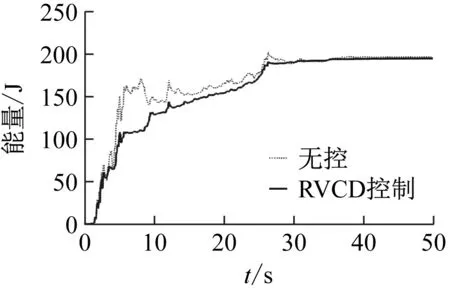
Nmax (29) 控制算法的性能由Q=[c1,c2,c3,h,φ,κ]这些控制参数所决定,为便于搜寻,Q应该满足一定取值范围: Q∈W (30) 式中,W为Q中各参数的取值范围。 所以本文将基于PSO算法优化RVCD,在满足控制转矩的约束条件下找到最优目标函数值对应的控制参数。 其具体优化流程如图3所示。 图3 粒子群算法优化流程图Fig.3 Flow chart of weighting matrices using PSO 为探究采用RVCD控制的减振效果与鲁棒性,本文选用一个单层框架结构进行仿真,被控结构质量为983 kg,刚度为2×105N/m,阻尼为390 N·m/s。为减轻结构自重,实际工程中AMD与结构质量比一般不超过5%,本文RVCD系统与结构质量比取为2%,旋转半径取为0.15 m,则转动惯量为0.44 kg·m2。可计算出方程(10)参数:ε=0.099 2,Cd=0.027 5。 S函数是系统函数(system function, SF)的简称,在 MATLAB中具有特定的语法格式,能够以代码的形式实现Simulink中的模块功能,适合于复杂动态系统的数学描述。本文分别编写了被控结构响应求解以及滑模控制算法模块的S函数,并在Simulink环境下进行了仿真,其仿真模型如图4所示。 图4 RVCD控制系统仿真模型Fig.4 Simulation model of RVCD control system 施加0.05 m的初始位移激励,并与无控结构、TMD控制结构进行比较,其结果如图5所示。 取系统稳态误差为±5%[19]。假设为结构位移降低到初始位移5%所用的时间。由图5可知,不施加控制时,ts大于10 s;采用TMD控制时,系统在4.66 s到达稳定;采用RVCD控制时,系统在2.40 s时到达稳定。 图5 初始位移激励下结构位移响应Fig.5 Structural displacement response under initial displacement excitation 实际工程中,结构的模型参数会存在不确定性,这需要控制器具有良好的鲁棒性。考虑恶劣情况,分别将结构的质量增加15%,刚度减少15%,采用RVCD进行仿真,结果如图6和图7所示。 图6 质量增加15%结构位移响应Fig.6 Structural displacement response with 15% mass increase 图7 刚度减少15%结构位移响应Fig.7 Structural displacement response with 15% stiffness decrease 由图6和图7可以发现,当结构质量增加15%,TMD控制时,系统稳定时间由4.66 s增加7.40 s,增加58.8%;RVCD进行控制时,系统到达稳定的时间并无明显变化,仅由2.40 s增加到2.85 s,增加到18.7%。当刚度减少15%时,结论类似。这说明当结构模型存在不确定性时,RVCD具有良好的鲁棒性。 为进一步研究RVCD抵抗外界干扰的能力,考虑了地震输入,选用El Centro波(1940,NS)进行仿真,地震波幅值为2 m/s2,其仿真结果如图8~图10所示。 图8 地震激励下结构位移响应Fig.8 Structural displacement response under earthquake wave 图9 RVCD转角位移Fig.9 Angle of rotary vibration control device 图10 RVCD输出转矩Fig.10 Output torque of rotary vibration control device 由仿真结果可知,在地震激励作用下,采用RVCD进行控制时,结构峰值位移与无控结构相比,下降了42%,这说明RVCD具有很好的减振效果。 实际AMD设计中,由于考虑到AMD控制系统安全性、安装空间、成本或减轻结构自重等因素,AMD参数的设计往往会受到限制,如AMD的质量,最大行程等。这就需要AMD在这些参数受限的情况下仍具有良好的控制效果,故在此对RVCD在地震作用下系统参数偏离时对结构振动控制的有效性进行分析,并与传统的直线AMD和TMD进行对比。其中,AMD采用LQR算法进行设计,权矩阵Q和R的待定系数取为:α=104,β=1。TMD的最优参数按Tsai等[20]提出的优化方法取值。定义峰值位移的减振效果为 (31) 式中,xu max和xc max分别为无控和施加控制后结构的最大位移。 由图11可看出,随着质量比的增加,TMD、直线AMD、RVCD的减振效果均逐渐增加,直线AMD效果略好于RVCD。TMD控制效果明显差于上述两种控制装置,无论质量比取何值,其最大的峰值位移减振效果小于另外两种控制装置最小的峰值位移减振效果。当质量比由0.05下降到0.01时,RVCD的减振效果仍有34.16%,说明其在质量受限的情况下仍具有良好的鲁棒性。 图11 结构峰值位移减振效果与质量比的关系Fig.11 Relationship between vibration reduction effect of peak displacement and mass ratio 调整LQR算法中的参数Q和R,可以得到直线AMD减振效果与质量块行程的关系,从图12的结果可以看出,当质量块的最大行程由0.202 m减少到0.1 m时,结构的减振效果由50.17%下降到25.15%。这说明在建筑空间受限的情况下,AMD无法按理想的最大行程设计,结构的减振效果下降显著。而RVCD控制时,质量块作旋转运动,无行程限制。安装空间主要会限制装置的旋转半径,图13给出旋转半径对控制效果的影响。当半径r由0.2 m减小到0.1 m时,结构的峰值位移减振效果略有下降,仅由45.38%下降到40.14%,说明在安装空间受限的情况下,RVCD比直线AMD具有更好的控制效果。 图12 直线AMD控制时结构峰值位移减振效果与质量块行程的关系 Fig.12 Relationship between vibration reduction effect of structural peak displacement and mass stroke under linear AMD control 图13 RVCD控制时结构峰值位移减振效果与旋转半径的关系Fig.13 Relationship between vibration reduction effect of structural peak displacement and rotation radius under control of RVCD 结合之前分析结果,结构RVCD控制系统具有很强的鲁棒性,在结构模型参数变化和自身物理参数受限的情况下仍具有很好的控制效果。 为进一步提升滑模控制器的控制效果,现用粒子群算法结合上述构造的目标函数(J)对滑模控制算法中的参数进行优化,仍采用上述结构在地震激励下进行仿真优化。经试算,Q取值范围{c1,c2,c3∈[0.5,50],h∈[1,10],κ∈(0,10],φ∈(0,1)}。权系数λ1和λ2分别取0.8和0.2。最终的优化结果如图14~图19所示。最优参数取为:[c1,c2,c3,h,κ,φ]=[6.32,10.26,5.54,5.71,4.39,0.39]。 图14 粒子群算法迭代结果Fig.14 Iterative results of PSO 图15 无控结构能量时程Fig.15 Energy time history of uncontrolled structures 图16 RVCD控制时结构能量时程Fig.16 Energy time history of structures under control of rotary vibration control device 图17 地震输入能对比Fig.17 Comparison of seismic input energy 图18 结构自身耗能对比Fig.18 Comparison of energy dissipation of structures 图19 结构动能和弹性势能之和对比Fig.19 Comparison of the sum of structural kinetic energy and elastic potential energy 从图15可以看出,整个地震响应过程中系统的能量是守恒的。地震前期较为剧烈,因此输入能和结构的阻尼耗能增加很快,结构的动能和弹性势能也较大。随着地震的强度下降,输入能和结构的阻尼耗能渐渐稳定,而动能和弹性势能慢慢慢减小到0,能量最终几乎全部由结构自身阻尼消耗掉。 从图16~图19可以看出,采用RVCD进行控制后,由于主动控制力做负功而承担了大部分的能量,结构最终自身阻尼耗能下降了81.6%,前期的动能和弹性势能峰值减小了62.8%。这说明采用RVCD进行控制时,能量大部分由主动控制装置承担,结构的自身承担的能量很少,RVCD起到了保护结构的作用。 为验证所优化参数结果,选取通过试算得到的一般解进行对比。从表1可以看出,在最优参数控制下,其控制效果要明显优于未优化参数的控制效果。 表1 优化前后减振效果对比Tab.1 Comparison before and after optimization 对于所提出的回转式振动控制装置(RVCD),通过理论分析和数值仿真,得到了以下主要结论: (1) 本文所提出的RVCD以及所设计的控制方法能有效控制结构振动,并且对模型参数的不确定性和外界干扰具有很强鲁棒性。在初始位移激励下,当结构质量增加15%或刚度减小15%时,TMD控制时系统到达稳态的时间增加了60%左右;RVCD控制时系统的稳态时间增仅加了19%左右。当系统受到2 m/s2的地震作用时,RVCD系统的减振效果达到42%。 (2) 结构RVCD控制系统对装置物理参数的改变具有不敏感性。当质量比由0.05下降到0.01时,RVCD的峰值位移减振效果仍有34.16%。当半径r由0.2 m减小到0.1 m时,结构的减振效率仍有40.14%,而直线AMD最大行程由0.2 m减少到0.1 m时,减振效果下降到25.15%,这说明在建筑空间受限的情况下,RVCD比直线AMD能发挥很好的控制效果,RVCD能有效解决直线AMD的行程问题。 (3) 采用PSO结合AMD做负功的优化方法表明:RVCD通过主动控制力做负功,承担了地震输入的大部分能量,明显减小了结构的能量响应,结构阻尼耗能下降了81.6%,结构的动能和弹性势能之和的峰值减小了62.8%。 (4) 对于滑模控制算法中控制参数的选取问题,从能量角度构造目标函数结合粒子群优化算法能够确定算法的最优参数值。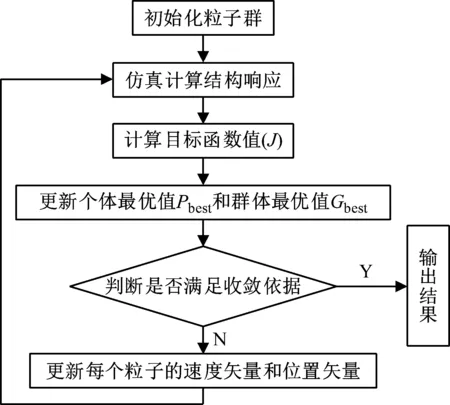
3 仿真分析
3.1 RVCD控制系统的仿真模型

3.2 控制系统的有效性及鲁棒性分析





3.3 RVCD系统参数分析

3.4 粒子群算法优化滑模控制参数结果





4 结 论

