汽车减振器锥形圆环缝隙流与阀片动态开度研究

马世榜， 高 原,2， 黄荣杰， 李 超

(1.南阳师范学院 机电工程学院，河南 南阳 473061; 2.郑州大学 机械与动力工程学院，郑州 450001)

汽车减振器用于吸收路面传来的振动，改善汽车行驶平稳性和乘坐舒适性，不同用途的汽车所需减振器的减振性能也不相同[1-3]。减振器的减振性能由阻尼特性决定，与减振器阀系中阀片的变形关系密切。带缓冲弹簧的双筒式减振器工艺简单、便于维修、阻尼力大且易于调整，在汽车行业有较为广泛的应用。

国内外学者对减振器的研究主要集中在阀片变形的解析解以及阻尼特性仿真建模上。例如：Panthi等[4-6]利用能量法建立起阀片弯曲变形的总势能方程，将阀片力学微分方程转化为弹性势能极值问题，得出阀片弯曲变形理论表达式；周长城等[7-8]根据薄板理论，建立了阀片弯曲变形的微分方程，计算出了阀片任意半径处弯曲变形的通解表达式，建立了阀片的变形与受到压强之间的关系；贺李平等[9]基于钱氏摄动法推导出了环形阀片刚度曲线方程，并根据有限元法仿真数据，拟合出待定系数，从而得到环形阀片大挠曲变形的解析解。上述研究都旨在找出阀片变形与受到压强之间的关系，阀片受到的压强主要由流体通过阀片变形形成的缝隙产生。

减振器阀片受力弯曲产生锥形圆环缝隙，但目前并未有学者对流体通过锥形圆环缝隙产生的压强进行研究。在计算阀片受到的压强时，通常将阀片打开后形成的锥形圆环缝隙近似地按照等高圆环缝隙或者厚壁小孔理论计算。然而流体通过锥形圆环缝隙、等高圆环缝隙和厚壁小孔产生的压降差距较大，尤其是在减振器处于中低速，阀片变形幅度较小时，按照等高圆环缝隙或者厚壁小孔理论计算阀片受到的压强均有较大误差。而且阀片变形和受到压强之间是相互耦合关系，阀片在流体载荷作用下产生变形，阀片的变形又改变了流体对阀片的作用力从而影响阀片的变形，正是这种相互作用使阀片开度处于动态平衡状态，现有计算一般按照阀片的最大开度计算阻尼值，忽略了阀片从关闭状态到最大开度的过程，存在一定误差。

在减振器阻尼特性仿真建模方面，现有学者一般采用MATLAB或AMESim软件，如段福斌等[10-12]。但在构建数学模型时，通常忽略阀片打开后阀片常通孔的流量，但在阀片打开初期或减振器低速运动阀片打开幅度较小时，仍有较多流体通过阀片常通孔，不能被忽略；阀片的开阀速度大多按照工程经验获得，并没有准确的解析解；而且也没有考虑流体冲击力对阻尼力的影响，存在一定误差，影响设计、计算的精确度，进而影响减振器的性能。

为解决上述存在的问题，本文推导出了锥形圆环缝隙流的运动微分方程，得出了流体通过阀片变形后所产生的锥形圆环缝隙压降与流量之间的关系。分析了阀片开阀前后的受力状态，考虑了流体对阀片的冲击力、阀片上下表面压力差以及弹簧刚度和预紧力等因素，提出了减振器开阀速度、阀片打开后常通孔流量、阀片动态开度的数学模型，为减振器阻尼特性研究提供了参考。

1 双筒式减振器工作原理

1.1 双筒式减振器的结构

双筒式减振器的结构如图1所示，主要由活塞杆、活塞阀系、底阀阀系、上腔、下腔、储油腔等组成。减振器的阻尼力靠活塞往复运动，使流体通过活塞阀系和底阀阀系产生。复原行程中，补偿阀一直打开，复原阀需要流体达到一定压力打开；压缩行程中，流通阀一直打开，压缩阀需要流体达到一定压力打开。减振器的阻尼特性与活塞的位移直接相关，活塞速度的大小，关系着复原阀片和压缩阀片的打开程度。

1.上腔;2.活塞阀系;3.下腔;4.储油腔;5.底阀阀系;6.压缩阀片;7.补偿阀片;8.缓冲弹簧;9.复原阀片;10.流通阀片;11.活塞杆。图1 双筒式减振器结构图Fig.1 Structure diagram of the double-tube damper

1.2 油液流动模型

复原行程油液分两部分流动，一部分油液经活塞阀系由上腔流到下腔，另一部分经底阀阀系由储油腔流至下腔，如图2所示。流经活塞阀系的油液同时通过活塞与油缸内壁的缝隙以及活塞孔。当复原阀未打开时，通过活塞孔的油液再流经复原阀片常通孔形成压差，复原阀常通孔与活塞孔串联后与活塞缝隙并联。当复原阀片打开时，通过活塞孔的油液同时流经复原阀片常通孔和复原阀片打开后形成的锥形圆环缝隙从而形成压差，复原阀常通孔与复原阀片打开后形成的锥形圆环缝隙并联后与活塞孔串联再与活塞缝隙并联。流经底阀阀系的油液，先通过底阀补偿孔，再流经补偿阀使补偿阀阀片打开形成压差，底阀补偿孔与补偿阀串联。

图2 复原行程油液流动示意图Fig.2 Schematic diagram of fluid flow in the recovery stroke

压缩行程中，油液也分两部分流动，一部分油液经底阀阀系由下腔流到储油腔，另一部分经活塞阀阀系由下腔流至上腔，如图3所示。当压缩阀片未打开时，油液先通过阀座孔再流经压缩阀片常通孔，形成压差，阀座孔与压缩阀常通孔串联。当压缩阀片打开时，油液通过阀座孔后同时流经压缩阀片常通孔和压缩阀片打开后形成的锥形圆环缝隙从而形成压差，压缩阀片常通孔与压缩阀片打开后形成的锥形圆环缝隙并联后与阀座孔串联。流经活塞阀系的油液，同时通过活塞与油缸内壁的缝隙以及流通孔，通过流通孔的流体会使流通阀打开，流通孔与流通阀串联后与活塞缝隙并联。

图3 压缩行程油液流动示意图Fig.3 Schematic diagram of fluid flow in the compression stroke

2 数学模型的构建

2.1 阻尼力计算

减振器的阻尼力F如式(1)所示，主要由活塞上下面压差形成，活塞在运动过程中也受到摩擦力的作用。

F=p1(Ah-Ag)-p2Ah+Ff

(1)

式中：Ah为活塞面积；Ag为活塞杆面积；p1为上腔压强；p2为下腔压强；Ff为活塞与油缸内腔摩擦力。

由于流通阀片薄且刚度低，一般认为，压缩工况流通阀片完全打开，节流阻尼很小，可以忽略不计。为了改善阻尼特性，储油腔内充有压缩气体，在计算时必须考虑在内。活塞与油缸内腔的摩擦力一般根据试验获得。

2.2 孔阀节流理论

活塞缝隙可以看作是一端移动的平行圆环缝隙，因此流体流经活塞缝隙产生压降Δpfh与流量Qfh之间的关系如式(2)所示

(2)

式中：dh为活塞缸内直径；δfh为活塞缝隙的宽度；μ为油液黏度；lfh为缝隙长度;v为活塞运动速度，复原行程为正，压缩行程为负。

活塞孔属于细长孔，流体流经活塞孔产生压降Δpfk与流量Qfk之间的关系如式(3)所示

(3)

式中：Nfk为活塞孔数量；dfk为活塞孔直径；lfk为活塞孔长度。

复原阀常通孔属于厚壁小孔，流体流经复原阀常通孔产生压降Δpfc与流量Qfc之间的关系如式(4)所示

(4)

式中：Cfc为复原阀常通孔流通系数；Afc为复原阀常通孔面积；Nfc为复原阀常通孔数量；ρ为油液密度。

流体流经复原阀常通孔产生的压降受流体沿程的阻力损失以及流体方向突然改变、流体面积突然减小等因素影响。这些因素用流通系数Cfc表示，由沿程阻力系数和各段局部阻力系数确定，关系如式(5)所示

(5)

式中：λ为沿程阻力系数；lfc为沿程阻力长度；dfc为沿程阻力直径; ∑ζ为各段局部阻力系数之和。

3 锥形圆环缝隙流

3.1 锥形圆环缝隙流压降计算

阀片打开后，靠近内径一端由于锁紧螺母的限制不发生变形，靠近外径一端受到流体冲击力和上下压差作用发生变形，从而形成锥形圆环缝隙，如图4所示。

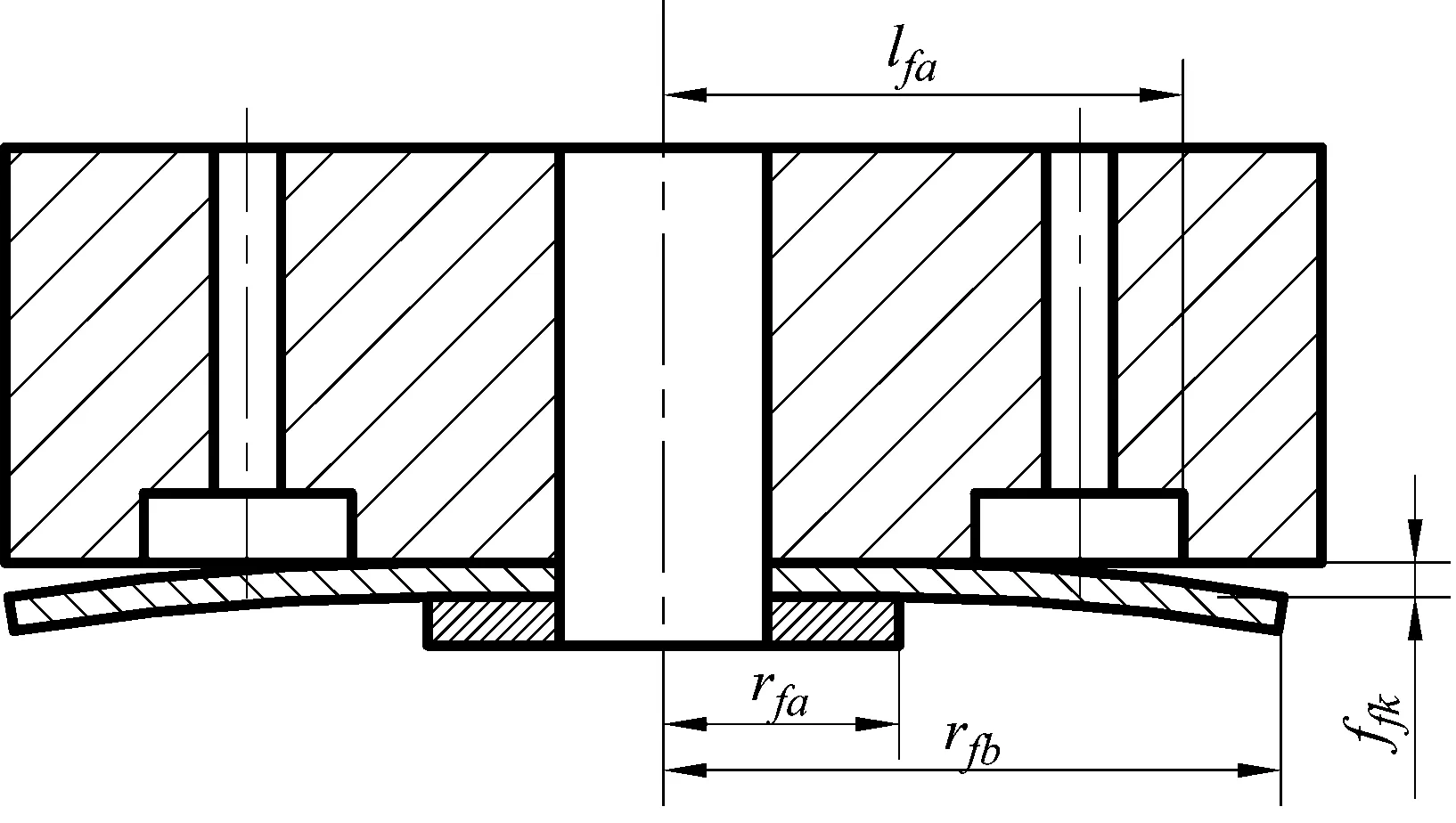
(a) 减振器节流阀

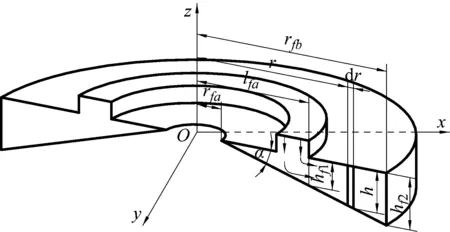
(b) 锥形圆环缝隙图4 锥形圆环缝隙示意图Fig.4 Schematic diagram ofconical ring gap

锥形圆环缝隙流的流体运动微分方程、速度方程与平行平面缝隙流时的流体运动微分方程和速度方程是一致的，如式(6)所示

(6)

式中：du为流体微元的径向速度；dz为流体微元的高度；dp为流体微元的压强；dr为流体微元的径向宽度。

将式(6)两边积分，并将边界条件z=0，u=0；z=h，u=0；代入得径向速度u，如式(7)所示

(7)

则通过锥形圆环缝隙的流量Qff如式(8)所示

(8)

即

(9)

其中h是关于r的函数，如式(10)所示

h=(r-rfa)tanα

(10)

式中,α为锥形圆环缝隙夹角。

将式(10)代入式(9)中得

(11)

将式(11)两边积分得

(12)

利用边界条件：r=lfa，p=pf1，可得定积分常数项C，如式(13)所示

(13)

其中

(14)

将边界条件r=rfb，p=pf2，以及式(13)、(14)代入式(12)中可得阀片变形产生的锥形圆环缝隙流压差与流量的关系，如式(15)所示

(15)

将阀片内半径rfa、阀片外半径rfb、活塞孔远端到活塞中心距离lfa等固定参数归到一常数项锥形圆环缝隙阻尼系数pl，如式(16)所示

(16)

则流体通过锥形圆环缝隙产生压降Δpff与流量Qff之间的关系可以表示为

(17)

减振器阀片内半径一般不为0，当阀片内半径rfa=0时，为特殊情况的锥形圆环缝隙流。可将rfa=0代入式(10)或对式(15)求极限的方法获得，两者结果一致，如式(18)所示

(18)

式中：ffk为阀片的开度；rfa为阀片内半径；rfb为阀片外半径；lfa为活塞孔远端到活塞中心距离。

3.2 锥形圆环缝隙阻尼系数pl的物理意义

锥形圆环缝隙流通系数pl为无量纲单位，受阀片内半径rfa、阀片外半径rfb、活塞孔远端到活塞中心距离lfa影响。其它条件一致时，阀片内半径rfa越大、阻尼系数pl越大；阀片外半径rfb越大，阻尼系数pl越大；活塞孔远端到活塞中心距离lfa越小，阻尼系数pl越大。其物理意义是流体通过该区域阻尼的比例系数，体现了流体通过该区域的能力，阻尼越大，流体越难通过该区域，压降越大。锥形圆环缝隙流通系数pl用于计算流体分别通过锥形圆环缝隙和阀片常通孔的流量，以及流体通过锥形圆环缝隙产生的压降。

3.3 现有计算方法偏差

阀片在流体力作用下弯曲变形，形成圆弧状轮廓。但由于阀片实际变形较小，最大开度往往在0.5 mm以下，圆弧状阀片弦高很小，可以忽律不计。因此，本文3.1节中提出的压降计算方法将流体通过阀片变形产生的圆弧状轮廓近似地看作锥形圆环缝隙进行计算。如图5所示。

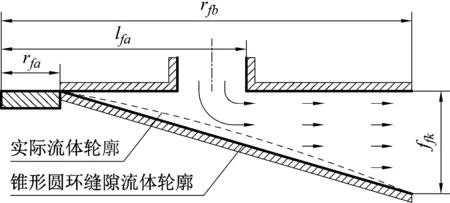
图5 锥形圆环缝隙流体示意图Fig.5 Schematic diagram ofconical ring gap

阀片变形引起的流体压降的现有计算方法，通常忽略阀片变形对流体轮廓的影响，将实际圆弧状流体轮廓看作等高圆环缝隙轮廓，如图6所示，流体通过等高圆环缝隙产生的压降Δpfd计算公式如式(19)所示。该计算方法，增加了流域面积，仅考虑了阀片外半径rfb、活塞孔远端到活塞中心距离lfa、阀片开度ffk对压降的影响，存在一定误差。与锥形圆环缝隙压降计算方法式(17)相比，忽略了阀片内半径rfa对流体压降的影响。

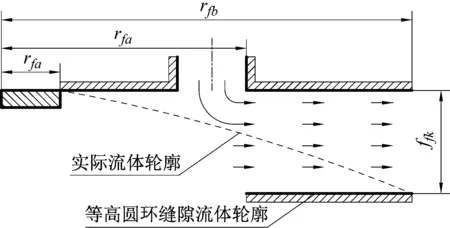
图6 等高圆环缝隙流体示意图Fig.6 Schematic diagram of ring gap

(19)

也有部分学者在计算阀片变形引起的压降时，将阀片打开后形成的通道直接看作厚壁小孔，如图7所示，流体通过厚壁小孔产生的压降Δpfh计算公式如式(20)所示。该计算方法，极大的增加了流域面积，仅考虑了阀片开度ffk对压降的影响，误差较大。与锥形圆环缝隙压降计算方法式(17)相比，忽略了阀片内半径rfa、活塞孔远端到活塞中心距离lfa对流体压降的影响；与等高圆环缝隙压降计算方法式(19)相比，忽略了活塞孔远端到活塞中心距离lfa对流体压降的影响。而且流通系数Cfb通常依靠经验结合试验获得，工作量较大。

(20)

其中

Afb=2πrfbffk

(21)

式中,Afb为厚壁小孔出口面积。

将式(17)、(19)、(20)在MATLAB环境下建模，三者对比仿真结果如图8所示。

由图8可见，锥形圆环缝隙压降同时受阀片开度ffk、阀片内半径rfa、阀片外半径rfb、活塞孔远端到活塞中心距离lfa等因素影响；等高圆环缝隙压降仅受阀片开度ffk、阀片外半径rfb、活塞孔远端到活塞中心距离lfa等因素影响；厚壁小孔压降仅受阀片开度ffk、阀片外半径rfb等因素影响。因此，按照锥形圆环缝隙来计算阀片打开后产生的压降，更贴近真实情况。

4 阀片动态开度的计算

4.1 阀片开阀速度的计算

阀片在开阀之前受到流体力Fl0，弹簧对阀片的预紧力F0以及活塞阀对阀片的支撑力FN，当流体力Fl0等于弹簧对阀片的预紧力F0，即活塞阀对阀片的支撑力FN=0时，阀片打开。

阀片的打开条件

Fl0=F0

(22)

阀片打开瞬间受到的流体力Fl0分为两部分：流体流经活塞孔后对阀片的冲击力Fc0，以及流体流经阀片常通孔产生压降对阀片的作用力Ffc0。

Fc0=ρQfh0vfk

(23)

式中：Qfh0为阀片打开瞬间通过活塞孔的流量；vfk为阀片打开瞬间流体通过活塞孔的速度。

(24)

式中：Qfc0为阀片打开瞬间阀片常通孔的流量；Aff为阀片面积。

其中：

(25)

Qfh0=Qfc0=Qfk0=(Ah-Ag)vh

(26)

式中：Qfk0为阀片打开瞬间活塞运动产生的流量；vh为阀片开阀速度。

将式(23)、(24)、(25)、(26)代入式(22)中得

(27)

将油液密度ρ、活塞面积Ah、活塞杆面积Ag、活塞孔数量Nfk、活塞孔面积Afk、阀片面积Aff、复原阀常通孔流通系数Cfc、复原阀常通孔面积Afc、复原阀常通孔数量Nfc；为等固定参数归到一常数项阀片打开系数pm，如式(28)所示

(28)

则开阀速度vh的计算公式为

(29)

4.2 阀片打开后常通孔流量的计算

阀片打开后，流体同时流经阀片常通孔与复原阀片打开后形成的锥形圆环缝隙，两者形成并联管道，压降相等。

Δpfc1=Δpff

(30)

式中：Δpfc1为阀片打开后流经阀片常通孔产生的压降。

将式(4)、(17)代入式(30)中得

(31)

将锥形圆环缝隙流通系数pl，减振器油的黏度、密度，以及复原阀常通孔流通系数、面积、数量等固定参数归为一常数项流量分配系数pn，流量分配系数pn用于表示阀片打开后，锥形圆环缝隙流与阀片常通孔的流量分配情况，如式(32)所示

(32)

则：

(33)

流体流经阀片常通孔Qff与复原阀片打开后形成的锥形圆环缝隙的流量Qfc1之和等于活塞运动产生的流量Qfk。

即：

Qff+Qfc1=Qfk

(34)

将式(33)代入式(34)中解一元二次方程，略去负项即可得到阀片打开后，流体流经锥形圆环缝隙的流量Qff与活塞运动产生的流量Qfk之间的关系，如式(35)所示

(35)

其中：

Qfk=(Ah-Ag)v

(36)

将式(35)在MATLAB环境下建模，阀片打开后，阀片常通孔与锥形圆环缝隙流量对比仿真图如图9所示。

图9 阀片常通孔与锥形圆环缝隙流量对比图Fig.9 Flow distribution between the through hole and theconical ring gap

由图9可以看出，流体流经阀片常通孔的流量随着阀片开度的增大而减小，流体流经锥形圆环缝隙的流量随着阀片开度的增大而增大；在阀片打开初始阶段，由于开度较小，流体仍主要通过阀片常通孔。因此，在计算阻尼特性时，阀片打开后，仍不能忽略阀片常通孔的流量。

4.3 带缓冲弹簧的减振器阀片受力分析

当活塞速度较小时，阀片在缓冲弹簧预紧力F0作用下，处于关闭状态。当活塞速度v大于开阀速度vh时，阀片受到的流体力Fl1大于缓冲弹簧预紧力F0，阀片发生变形，此时阀片产生抵抗变形的弹性力Ff，而且由于阀片变形，使缓冲弹簧压缩产生对阀片的弹簧力Fk。由于缓冲弹簧预紧力F0和弹簧力Fk，阀片的变形量减少，流体通过锥形圆环缝隙的阻力增加，从而提高了减振器的阻尼力。阀片变形后的力学模型如图10所示，阀片在流体力Fl1，弹簧对阀片的作用力Ft以及自身抵抗变形的弹性力Ff，三力作用下处于平衡状态，如式(37)

Fl1=Ft+Ff

(37)

图10 阀片力学模型Fig.10 Mechanical model of throttle-slices deformation

阀片在开阀之后受到的流体力Fl1分为两部分：流体流经活塞孔后对阀片的冲击力Fc1，以及流体流经阀片常通孔与阀片打开后形成的锥形圆环缝隙并联后产生压降对阀片的作用力Fff，如式(38)

Fl1=Fc1+Fff

(38)

其中：

(39)

Fff=ΔpffAff

(40)

弹簧对阀片的作用力Ft也分为两部分：弹簧的预紧力F0，以及阀片变形引起弹簧压缩产生的弹簧力Fk，如式(41)

Ft=F0+Fk

(41)

其中：

Fk=Kffk

(42)

式中,K为弹簧的刚度。

阀片自身抵抗变形的弹性力Ff，可以根据其他学者的研究得出[13]。

(43)

(44)

式中：Gr为阀片的变形系数，p为阀片受到的压力，h为阀片的等效厚度，Aff为阀片的面积。

将式(38)、(41)代入式(37)中可得带缓冲弹簧减振器阀片的受力平衡方程，如式(45)

Fc1+Fff=F0+Fk+Ff

(45)

4.4 带缓冲弹簧的阀片动态开度的计算

现有研究通常将阀片受到的压力p看作定值，但压力p与阀片开度ffk是一个动态平衡的过程。压力p是流体流经阀片常通孔与阀片打开后形成的锥形圆环缝隙并联后产生的压降，阀片在压力p的作用下打开产生变形，阀片变形的同时也会使阀片常通孔和锥形圆环缝隙的流量发生变化从而影响压力p的大小，两者相互作用时刻变化。而且，阀片受到缓冲弹簧的作用力也随阀片开度时刻变化。因此需要根据受力平衡求出当前时刻压力p的阀片开度ffk。

将式(36)、(39)、(40)、(42)、(44)以及弹簧预紧力F0，代入式(45)即可求出当前时刻活塞速度为v时，阀片开度ffk的值，如式(46)所示。该方程仅有阀片开度ffk一个未知量，但为一元高次方程，并无解析解，需要用计算机求出代数解。

(46)

阀片动态开度的计算步骤为：

步骤1根据式(29)计算阀片的开阀速度vh；

步骤2根据式(36)计算出当前时刻活塞运动产生的流量Qfk；

步骤3当前活塞速度v大于开阀速度vh时，根据式(16)计算锥形圆环缝隙阻尼系数pl；

步骤4将计算出的锥形圆环缝隙阻尼系数pl代入式(32)计算流量分配系数pn；

步骤5根据式(35)计算出当前时刻通过锥形圆环缝隙流量Qff，其中当前时刻阀片开度ffk未知；

步骤6根据式(17)，计算出当前时刻流体通过锥形圆环缝隙所产生的的压降Δpff，其中当前时刻阀片开度ffk未知；

步骤7分别根据式(39)计算出当前时刻流体对阀片的冲击力Fc1，根据式(40)计算出当前时刻流体通过锥形圆环缝隙对阀片的作用力Fff，根据式(42)计算出当前时刻弹簧压缩产生的弹性力Fk，根据式(44)计算出当前时刻阀片自身抵抗变形的弹性力Ff，其中当前时刻阀片开度ffk未知；

步骤8将式(39)、(40)、(42)、(44)以及弹簧的预紧力F0代入式(45)，构建当前时刻阀片的受力平衡方程，求出当前时刻阀片开度ffk；

步骤9根据活塞速度重复步骤5～8，求出任意时刻的阀片开度。

5 仿真与验证

根据汽车减振器台架试验标准QC/T 545—1999规定，在MTS 850型Damper Test System试验台(如图11)上采用正弦激励方式对减振器进行试验，并在MATLAB环境下搭建某带缓冲弹簧减振器模型进行仿真计算。

图11 示功机试验台Fig.11 Testing bench of indicator machine

5.1 模型验证

减振器主要结构参数如表1所示。

表1 减振器参数Tab.1 Parameters of shock absorber

对减振器进行示功试验并仿真，试验行程为±25 mm，得到0.1 m/s、0.3 m/s、0.5 m/s、0.8 m/s、1.0 m/s、1.3 m/s共6个速度点的示功图，试验所得示功图与仿真示功图对比如图12所示。

由图12可知：该减振器的仿真示功特性(虚线值)与试验结果(实线值)曲线趋势一致，符合程度很高，误差很小。证明了建模过程中，锥形圆环缝隙压降理论、阀片开阀速度理论、阀片打开后考虑阀片常通孔流量以及阀片动态开度计算理论的正确性。

5.2 锥形圆环缝隙流与现有计算方法对比

对减振器进行低速v=0.1 m/s、中速v=0.5 m/s、高速v=1.3 m/s示功试验并仿真，试验行程为±25 mm。并分别采用锥形圆环缝隙理论、等高圆环缝隙理论、厚壁小孔理论进行仿真。试验所得示功图与仿真示功图对比如图13所示。

由图13看出，当减振器处于v=0.1 m/s(低速)，v=0.5 m/s(中速)时，无论是按照等高圆环缝隙还是厚壁小孔计算，其仿真结果均与试验结果有较大差距，当v=1.3 m/s(高速)时，现有两种计算方法仿真结果与实验结果差异较小；而按照锥形圆环缝隙计算时，减振器的高、中、低速仿真曲线与试验曲线均保持一致。主要是由于，当减振器处于中低速时，阀片打开幅度较小，三种计算方法的流域面积差异较大，流体通过此区域产生的压降也差异较大；减振器速度较高时，随着阀片打开幅度的变大，此时三种计算方法的流域面积趋于一致，流体通过此区域产生的压降也趋于一致，三种计算方法受阀片开度的影响程度如图8(a)所示。验证了第3章提出的锥形圆环缝隙流的准确性和广适性。

5.3 阀片常通孔对阻尼特性的影响

分别考虑和不考虑阀片打开后常通孔流量，在v=1.0 m/s条件下进行建模仿真并与试验值进行对比，其结果如图14所示。

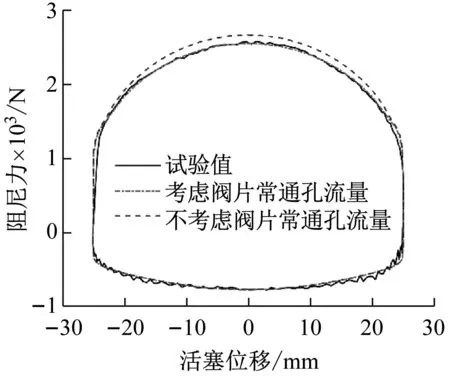
图14 阀片常通孔对减振器阻尼特性的影响Fig.14 The effect ofthe through hole on the shock absorber characteristic

由图14可以看出，不考虑阀片打开后常通孔流量时，阻尼力比实际值偏大，而考虑阀片打开时常通孔流量时，阻尼力与实际值基本一致。这是由于阀片打开后，仍有部分流体通过阀片常通孔，忽略此部分流量，会增加通过锥形圆环缝隙的流量，从而使阻尼力增大。因此在计算时，必须考虑阀片打开后常通孔流量。

6 结 论

(1) 利用锥形圆环缝隙阻尼系数pl，可以计算出流体通过汽车减振器阀片打开后形成的圆环缝隙产生压降与流量之间的关系。流体通过阀片打开后形成缝隙的压降与流量、阀片开度、阀片内半径、阀片外半径、活塞孔远端到活塞中心距离等均有较大影响。

(2) 带缓冲弹簧的汽车减振器阀片打开速度与阀片打开系数pm及缓冲弹簧预紧力F0有关。

(3) 阀片打开后仍有较多流体通过阀片常通孔，尤其是在阀片打开初期，在计算阻尼特性时，应将阀片常通孔流量考虑在内。阀片常通孔流量与阀片打开后缝隙流量分配受流量分配系数pn影响。

(4) 在计算减振器阀片开度时，应考虑阀片开度和流体压降的动态关系。