基于修正IDA法的隧道地震易损性分析

董正方， 刘淦之， 曾繁凯， 康 帅

(1.河南大学 岩土与轨道交通工程研究所，河南 开封 475004； 2.河南大学 河南省轨道交通智能建造工程技术中心，河南 开封 475004； 3.建业地产股份有限公司，郑州 450000)

地震易损性从宏观角度描述地震动强度与结构破坏程度之间的关系，已成为了评估结构地震风险强有力工具。

现阶段，对地上结构地震易损性的研究主要是建立易损性曲线的过程。对于易损性曲线的研究，早期多采用震害调查、专家评价等通过统计回归建立经验易损性曲线，张桂欣等[1]通过震害调查方法建立了北京市各类建筑结构的地震易损性曲线；陈力波等[2]基于汶川地震对桥梁震害调查建立了汶川地区公路桥梁系统的地震风险曲线。之后的研究者采用数值模拟进行结构响应的统计分析，并利用损伤指标建立具有明确概率意义的易损性曲线[3]。其发展过程与地震反应分析的发展实质上是同步的，从弹性谱法到非线性静力法,再到非线性时程分析法。Jernigan等[4]采用弹性谱法得到Memphis地区桥梁易损性曲线；Hwang等[5]采用Pushover法对美国东部受地震影响的高速公路系统进行易损性分析；钟德理等[6]对pushover法进行简化得出求解单体和群体建筑物易损性指数的方法，并通过易损性曲线来评价城市总体抗震性能。目前，增量动力分析(incremental dynamic analysis, IDA)法是易损性分析中应用最广泛的研究方法。Bertero[7]最早提出了增量动力分析方法的基本思想，随后IDA法被广泛用于桥梁和建筑的地震易损性分析中[8-13]。IDA法作为一种结构地震分析的手段，本质上是通过大量数值计算后借助统计学手段对结果进行分析。由于需要大量计算，在某种程度上限制该方法使用。对此Vamvatsikos等[14-17]对IDA法在不同结构实际应用中存在的不足进行了改进。

隧道的地震易损性研究滞后于地上结构。到目前为止，隧道的地震易损性分析主要基于以往的隧道破坏案例，采用专家判断或经验易损性曲线完成[18]。美国生命线联盟(ALA)[19-20]和HAZUS系统[21]以全世界隧道破坏案例数据为基础利用统计回归法得出不同类型隧道在不同PGA水平下经验易损性曲线。而被广泛应用于地上结构的解析方法在隧道易损性研究中应用十分有限。Argyroudis等[22]采用拟静力方法，对盾构隧道进行了易损性分析，并提出适用于地下结构的相对弯矩比性能指标。Huang等[23]在Argyroudis等研究的基础上，对山岭隧道进行了地震易损性研究。周志光等[24]以上海典型软土层某区间的地铁隧道为研究对象，基于IDA分析结果得到软土隧道的地震易损性曲线。

本文基于修正IDA法[25]，对地下管廊(市政隧道)和盾构隧道在不同场地类别、结构埋深、截面尺寸、结构型式等情况下的易损性进行分析，评估其抗震能力。

1 理论分析

1.1 修正IDA法

IDA法是用于评估地震动作用下结构性能的一种参数化分析方法。该方法是对地震动记录进行一定比例的调幅，调幅后的地震动强度作为结构输入进行动力时程计算。由于动力时程计算在地震作用下需要考虑土体的非线性和土-结构相互作用模型的动力边界效应，计算需要耗费大量的时间且容易出现不收敛。

针对上述问题，将动力时程法修正为反应加速度法进行计算。反应加速度法是地下结构抗震拟静力法中精度较高[26]、模型简单的一种方法，其计算过程需要结构反应和场地反应分开计算，结合IDA法的原理，提出修正IDA法，流程见图1。修正IDA法的场地计算采用成熟的一维场地分析，土体非线性采用等效线性本构，直接采用试验成果，避免不同非线性本构带来的离散性，且计算简单；反应加速度法模型是拟静力方法，对人工边界要求较低。因此提高了计算效率，且保证了计算结果不离散，使得地下结构进行大量IDA分析成为可能。

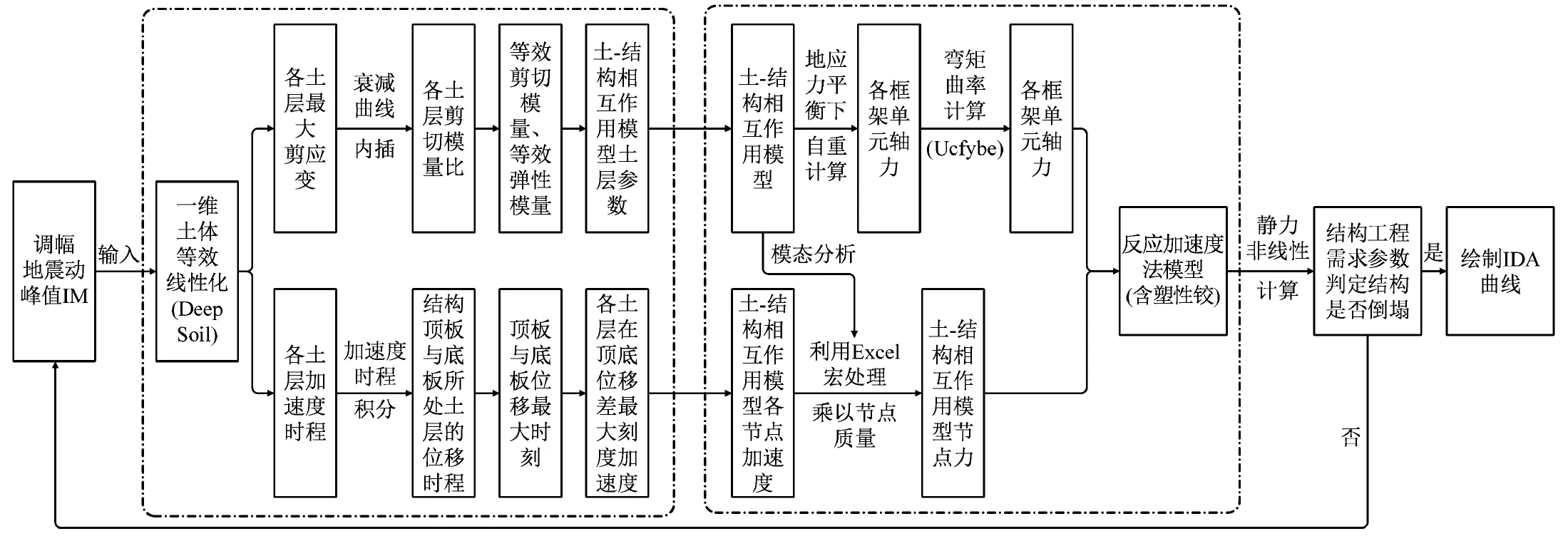
图1 修正IDA法流程图Fig.1 Flow chart of modified IDA

1.2 地震易损性

Baker等[27-28]指出工程需求参数EDP和地震动强度指标IM之间满足指数关系。本文假定工程需求参数的均值SD和IM之间也服从此关系，取自然对数得以下关系式

lnSD=a+blnIM

(1)

式中，回归系数a和b可以通过修正IDA计算得到的大量数据回归分析得到。

地震易损性曲线表示的是结构在不同地震动强度下结构的失效概率，这是一种在给定地震动强度指标情况下，结构反应超出结构能力限值的概率，是一种条件概率，即可表示为下式

(2)

式中:Pf表示结构的超越概率；C表示结构抗震能力，D表示结构的地震需求，C和D均为独立随机的变量，且均服从正态分布；SC表示结构抗震能力的均值，σC表示结构抗震能力的标准差，σD表示结构地震需求的标准差。由于式(1)是以IM为自变量的表达式，且本文仅考虑到地震动强度的随机性，并未考虑结构的随机性，所以σC在式(2)中等于0，而σD也是以IM为自变量的表达式，如下式

(3)

所以Pf可以表示为

Pf=P[D≥C|IM=X]=

(4)

式中，Φ(Χ)为标准正态分布函数。由式(4)得出不同结构性能标准所对应的超越概率，所得到的曲线就是我们要求得的地震易损性曲线，从而实现隧道的抗震性能评估。

2 算 例

2.1 工程背景

算例选用两种结构型式，一种是截面为矩形的地下管廊；另一种是截面为圆形的盾构隧道。地下管廊选取某市地下区间管廊其中一区段，盾构隧道选取某市轨道交通某段区间隧道，截取其中典型横向断面为计算截面。依据《城市轨道交通结构抗震设计规范》中的场地类别规定，通过土层等效剪切波速和覆盖层厚度划分场地。选取的土层厚度分别为50 m和90 m，地下结构埋深分别为5 m、10 m和36 m。具体结构横截面及Ⅰ、Ⅱ、Ⅲ、Ⅳ类场地的划分见图2。

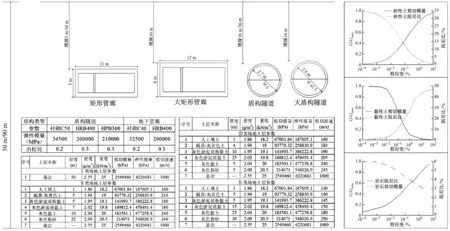
图2 结构横截面及土层参数Fig.2 Cross-section of structure and soil parameters

2.2 有限元建模及工况设置

有限元模型中土体采用平面应变单元模拟；结构简化为平面框架，沿地下结构纵向取单位长度，采用梁单元模拟，梁单元位置取在地下结构衬砌形心处，与土体之间采用刚臂连接，具体细节处理方式见图3(c)计算模型底面采用固定边界，顶面取地表面；侧面采用竖向约束的水平滑移边界，人工边界采取8倍的地下结构宽度[29]，见图3(a)、(b)。

管片接头处理方法有：惯用法、修正惯用法、多铰环法及梁-弹簧方法等[30]。其中惯用法和多铰环法是两个极端；修正惯用法采用经验参数近似考虑了接头影响。梁-弹簧方法从理论上来说最接近实际情况，这两种方法也是GB 50157—2013《地铁设计规范》建议的方法；但接头弹簧的参数确定一般是理论推导或接头试验得到，具有离散性，还不易推广。故本文采用修正惯用法，一般引入两个参数进行修正，一个是接头影响刚度下降的“抗弯刚度有效率η”，一个是错缝拼装影响的“弯矩的增加率ζ”(通缝拼装ξ为0)。对修正刚度模型求出其管片最大弯矩M，乘以(1+ζ)得到管片实际弯矩。由于η和ζ没有解析解，参考日本规范[30]给出了一些经验值，因为所选模型为平板形混凝土管片，又是错缝拼装的施工形式，故选“盾构工程用标准管片，土木学会”定义的η和ζ，取值分别为0.8和0.3。

考虑到地震动记录峰值、持时、频谱特性等因素，故从最不利地震动数据库和太平洋地震工程研究中心(PEER)选出40条地震波，使得所选择的地震波均匀分布在四类场地中如图4所示。

地震动峰值加速度如表1，采用上述的结构型式、场地类别以及地震动记录，列出以下分析工况如表2。其中工况10、12与工况3、7采用相同场地类别、土层厚度、埋深，不同的横断面大小作为区别；工况9、11分别以不同埋深与工况3、7作为区别。地下管廊埋深根据实际情况，埋深取为5 m与工况3埋深作比较；盾构隧道埋深取为最不利埋深设置为36 m[31]，与工况7埋深作比较。

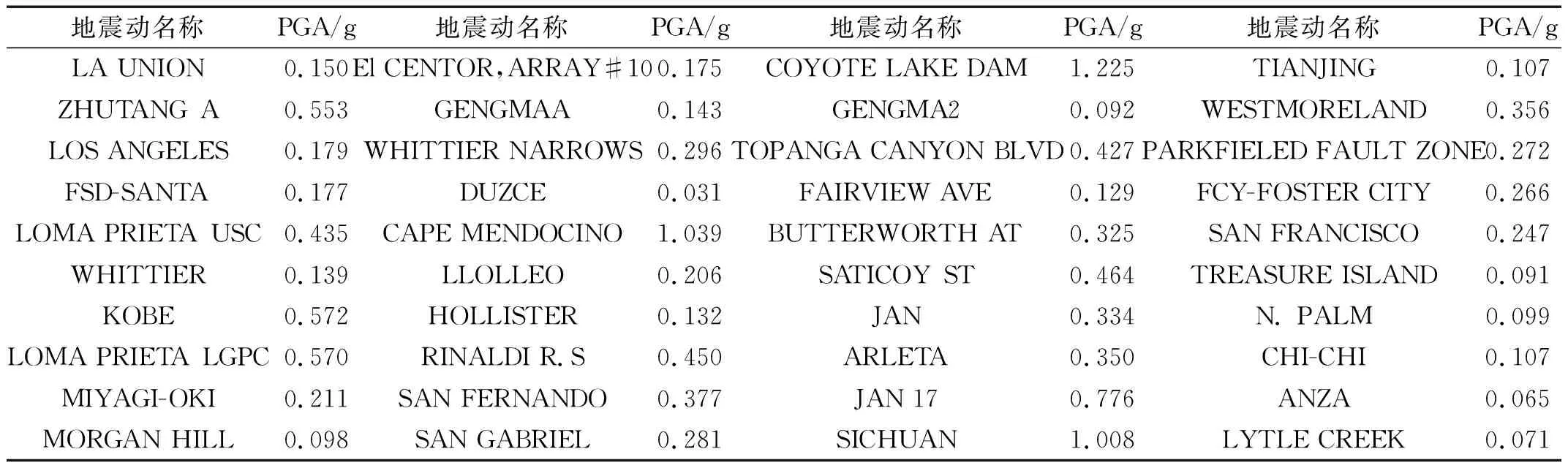
表1 地震动峰值加速度Tab.1 Summary of PGA

表2 工况设置Tab.2 Working condition setting

2.3 结构地震需求模型统计

基于修正IDA法得到上述十二种工况的IDA曲线，对各个离散点数据取自然对数，得到一系列数据点(lnEDPi,lnIMi)，将其绘制在平面坐标系中，并对这些离散点进行线性回归，得到各个工况结构的地震需求模型。

结合文献[32]，选用更能准确反映隧道抗震性能的地表峰值加速度(PGA)作为地震动强度参数。层间位移角作为地下管廊的变形指标，最大直径变形率作为盾构隧道变形指标，相对弯矩比作为地下管廊和盾构隧道的强度性能指标，地震需求模型汇总如图5、图6所示。

2.4 结构性能指标限值

本文以层间位移角、直径变形率和相对弯矩比作为隧道结构的工程需求参数(engineering demand parameter，EDP)。结合GB 50909—2014《城市轨道交通结构抗震设计规范》、GB 50157—2013《地铁设计规范》、GB/T 51336—2018《地下结构抗震设计标准》，将地下结构损伤定义为3级，如表3。

表3 抗震性能要求等级划分Tab.3 Classification of seismic performance requirements

地震作用下规范《地下结构抗震设计标准》指出，圆形断面地下结构弹性状态下直径变形率不应超过4‰；弹塑性状态下不应超过6‰。地下框架结构弹性阶段以钢筋混凝土地下结构构件出现塑性铰时的层间位移角作为结构弹性层间位移角限值，应取为1/550；弹塑性工作阶段，层间位移角限值应取为1/250。但目前规范均未给出地下结构在倒塌情况下的直径变形率及层间位移角限制。根据文献[33]，可以得出地下圆形断面结构在倒塌情况下的直径变形率限值为15.2‰；根据《地下结构抗震设计标准》结合文献[34]，通过统计分析美国Peer数据库和近年来的国内的试验数据，得出地下框架结构倒塌情况下的限值取为1/35。

对于相对弯矩比，根据国内的抗震设计规范，日本抗震设计规范和美国抗震设计规范，以及Argyroudis等提出的相对弯矩比的概念。同时在Qiu等[35-36]运用相对弯矩比作为工程需求参数对圆形断面隧道做的大量地震易损性研究的基础上，得出在划分三个抗震性能等级下的地下结构相对弯矩比的限值。

本文所取EDP对应的结构性能指标在不同性能水准下的取值，如表4。

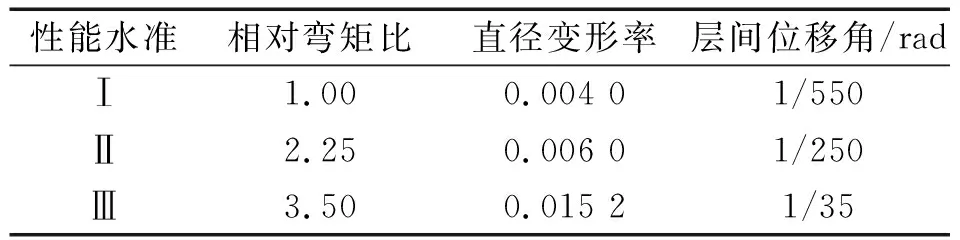
表4 结构性能指标Tab.4 Limit value of structure

3 地震易损性分析

3.1 不同场地类别

相同埋深，不同场地类别下盾构隧道和地下管廊易损性函数如表5，易损性曲线如图7、图8所示。

从图7、图8得出，处在不同场地类别的结构易损性曲线差别较大。以图7(b)为例，结构处在Ⅰ类场地较Ⅳ类场地，超越性能水准Ⅰ的概率在PGA达到1.1g时相差最大为96%；超越性能水准Ⅱ的概率在PGA达到2.7g时相差最大为92%；超越性能水准Ⅲ的概率在PGA达到4.3g时相差最大为88%，其他场地类别对比也相差较大，如Ⅱ类、Ⅲ类场地，结构超越性能水准Ⅱ的概率在PGA达到3.1g时相差最大为29%，Ⅲ类、Ⅳ类场地，结构超越性能水准Ⅱ的概率在PGA达到1.5g时相差最大为62%。由图中曲线的趋势可以看出，随着PGA的增大，曲线斜率有先增大后减小的趋势，且整个易损性曲线呈现S型；在性能水准Ⅰ状态下，超越概率随着PGA的增大上升坡度较陡，说明在地震作用下结构超越性能水准Ⅰ的可能性非常大；在性能水准Ⅱ和Ⅲ阶段易损性曲线的趋势较为平缓，说明在地震作用下超越概率较小，隧道结构在进入弹塑性工作阶段有较好的抗震能力。同时从易损性曲线采用不同的结构损伤指标可以看出，基于变形的角度和基于力的角度来看待结构的损伤程度有一定差别。同时通过对比不同类别场地两种结构型式的地震易损性曲线，得出在地震下的结构危险程度：Ⅳ类场地>Ⅲ类场地>Ⅱ类场地>Ⅰ类场地。

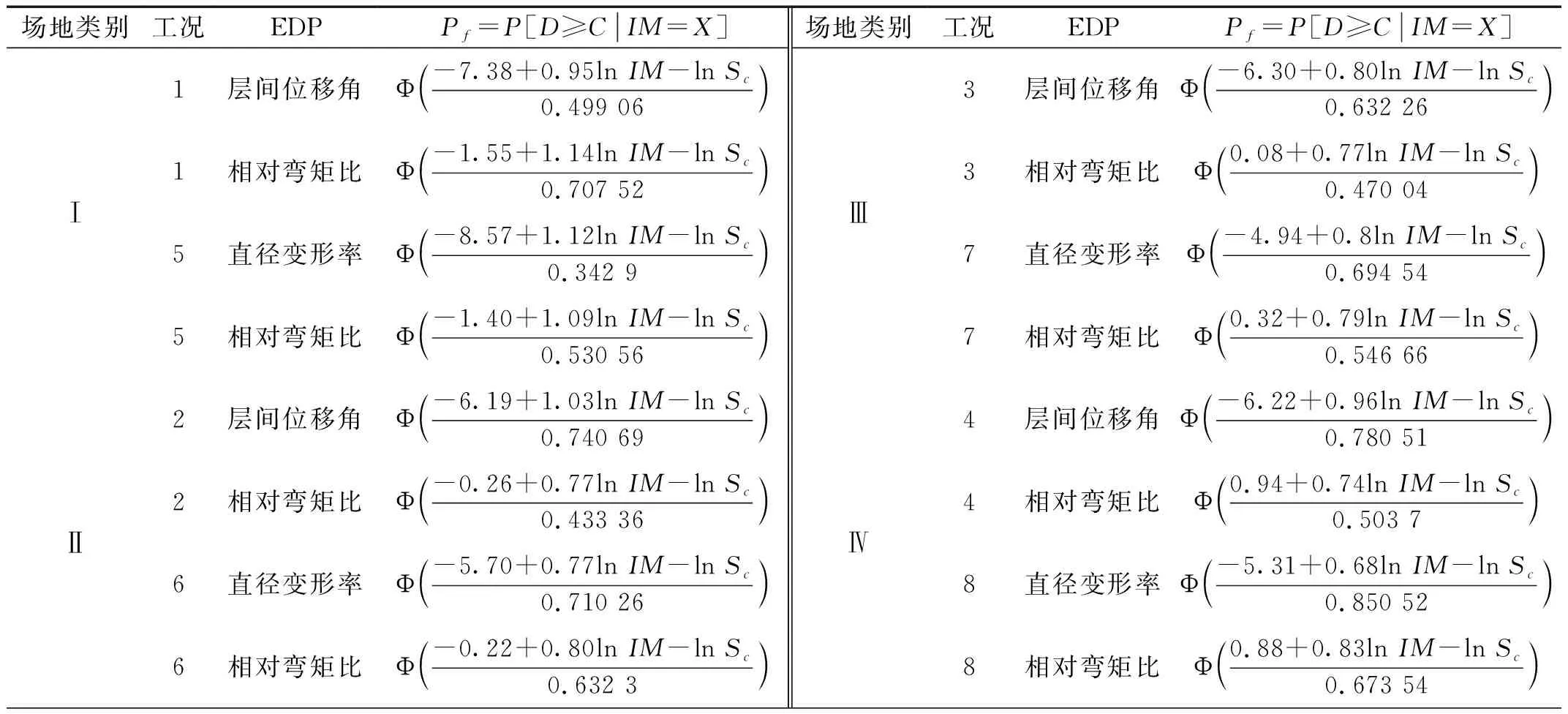
表5 不同场地类别对应工况下易损性函数Tab.5 The seismic fragility function in different sites

3.2 不同埋深

在Ⅲ类场地下，分别对比埋深5 m和10 m的地下管廊易损性以及埋深10 m和36 m的盾构隧道易损性，得到工况9和工况11的易损性函数如表6，对应易损性曲线如图9、图10所示。

表6 不同埋深易损性函数Tab.6 The seismic fragility functions of different depths

从图9、图10得出，由不同损伤指标得到的两种结构型式不同埋深下易损性曲线趋势较为接近。通过图9(a)具体分析，超越性能水准Ⅰ的概率在PGA达到1g时相差最大为1%；超越性能水准Ⅱ的概率在PGA达到5g时相差最大为2%；超越性能水准Ⅲ的概率在PGA达到5g时相差最大为2%，埋深5 m较埋深10 m地下管廊超越概率略有减小，说明埋深5 m的地下管廊损伤程度低于埋深10 m。图9(b)可以得到以相对弯矩比作为损伤指标来评价地下管廊地震易损性规律和层间位移角相同。图10可以得到，对于盾构隧道，埋深36 m的损伤程度要大于埋深10 m的，但差距并不明显。

3.3 不同截面尺寸

在Ⅲ类场地下，不同截面尺寸地下管廊与盾构隧道的地震易损性函数如表7，对应易损性曲线如图11、图12所示。

表7 不同截面尺寸易损性函数Tab.7 The seismic fragility functions of different structure types

图11(a)、图12(a)得出，以层间位移角、相对弯矩比为结构损伤指标，不同截面损伤程度差距较为明显。通过图11(a)具体分析，不同截面尺寸管廊，超越性能水准Ⅰ的概率在PGA达到0.6g时相差最大为35%；超越性能水准Ⅱ的概率在PGA达到1.4g时相差最大为26%；超越性能水准Ⅲ的概率在PGA达到5g时相差最大为6%。大截面比小截面的损伤概率更大，大截面在PGA达到1.5g的情况下，结构已经完全超出性能水准Ⅰ范围，而小截面在PGA达到3g状态下结构才完全超出性能水准Ⅰ状态。

图11(b)、图12(b)得出，以相对弯矩比为结构损伤指标，不同截面损伤程度差距不是很明显，但还是能看出大截面结构相比小截面更加危险。

综上所述，不同场地类别结构易损性曲线差别最大，两种结构型式不同场地类别的超越概率最大差值均达到约96%；其次，截面尺寸对结构易损性曲线也有一定影响，大、小管廊超越概率最大相差约35%，不同尺寸盾构超越概率最大相差约41%；结构埋深对易损性曲线影响最小，两种结构型式不同埋深下易损性曲线都较接近，超越概率最大差值均约为4%。因此，三种不同的影响因素对结构损伤程度的影响大小，场地类别>结构尺寸>结构埋深。

3.4 不同结构型式

结构损伤指标取相对弯矩比，对比不同场地类别，相同埋深下地下管廊与盾构隧道易损性曲线，见图13。

从图13(a)得出，Ⅰ类场地中，当PGA<2.8g，地下管廊超越性能水准Ⅰ概率大于盾构隧道；当PGA>2.8g，盾构隧道超越概率大于地下管廊；性能水准Ⅱ、Ⅲ概率均为地下管廊大于盾构隧道。从图13(b)得出，Ⅱ类场地中当PGA<1.7g，盾构隧道超越性能水准Ⅰ概率大于地下管廊；当PGA<1.7g，地下管廊超越概率大于盾构隧道；性能水准Ⅱ、Ⅲ概率均为盾构隧道大于地下管廊。从图13(c)得出，Ⅲ类场地中结构超越性能水准Ⅰ、Ⅱ、Ⅲ概率均为盾构隧道大于地下管廊，此时盾构隧道更安全。从图13(d)得出，Ⅳ类场地中，当PGA<0.1g，盾构隧道超越性能水准Ⅰ概率大于地下管廊，当PGA>0.1g，地下管廊超越概率大于盾构隧道；当PGA<0.6g，盾构隧道超越性能水准Ⅰ概率大于地下管廊，当PGA>0.6g，地下管廊超越概率大于盾构隧道；当PGA<1.4g，盾构隧道超越性能水准Ⅰ概率大于地下管廊，当PGA>1.4g，地下管廊超越概率大于盾构隧道。

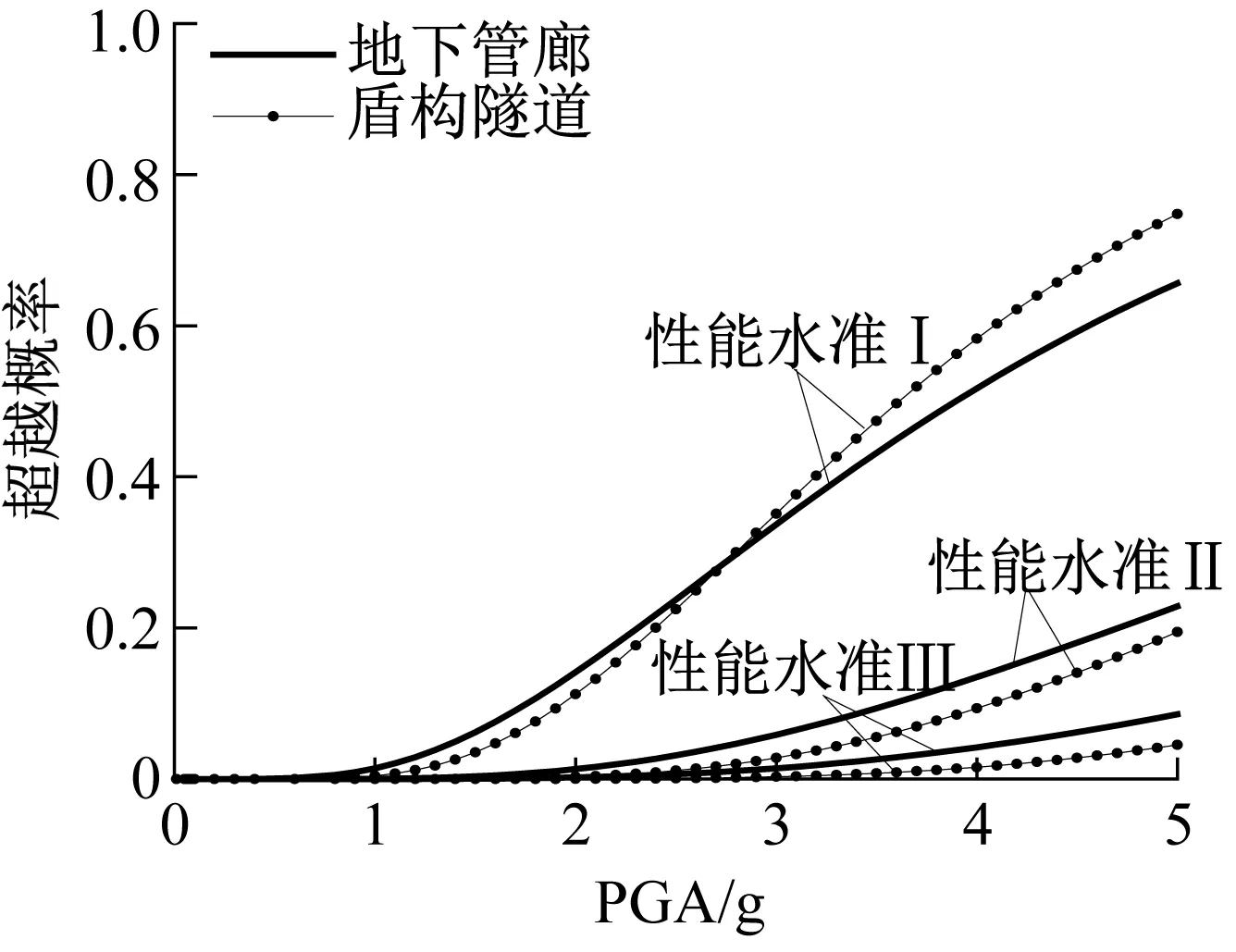
(a) Ⅰ类场地

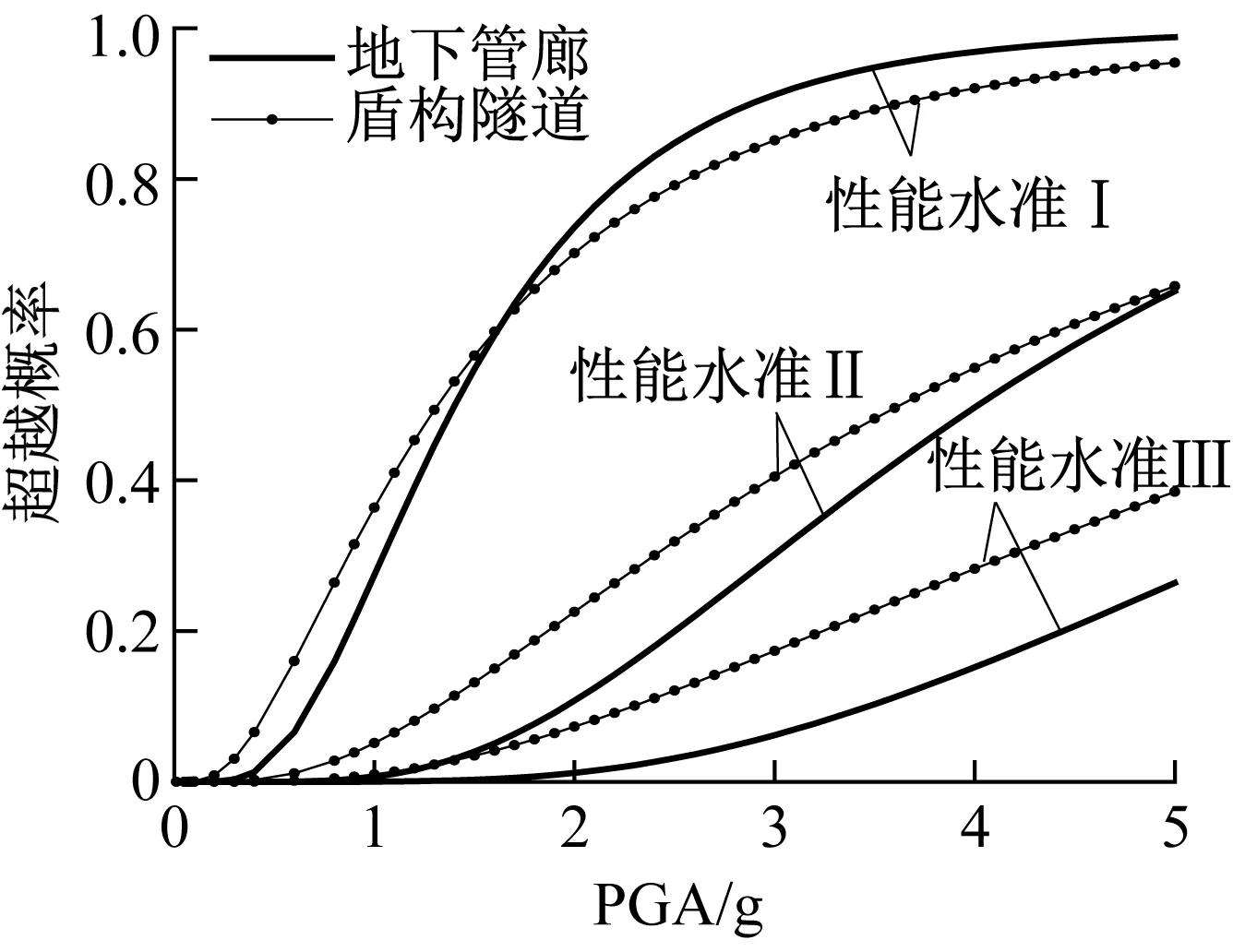
(b) Ⅱ类场地

(c) Ⅲ类场地

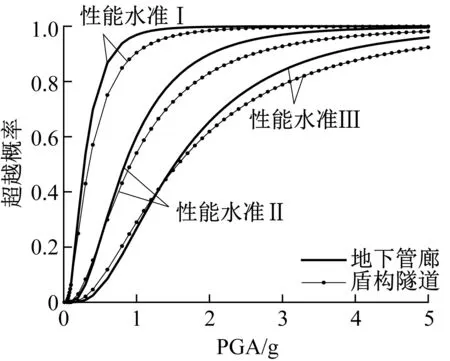
(d) Ⅳ类场地图13 不同结构型式易损性曲线Fig.13 The seismic fragility curves of different structural types

4 结 论

本文基于修正IDA法，通过对不同场地类别、埋深、截面尺寸的两种典型结构型式的隧道进行地震易损性分析，得到如下结论：

(1) 三种不同的影响因素对隧道结构损伤程度的影响大小，场地类别>截面尺寸>结构埋深。四种场地类别对隧道损伤程度影响大小：Ⅳ类场地>Ⅲ类场地>Ⅱ类场地>Ⅰ类场地。

(2) 隧道结构超越性能水准Ⅰ的可能性比较大，但超越性能水准Ⅱ和Ⅲ的可能性较小，说明隧道结构在进入弹塑性工作阶段具有较好的抗震能力。

(3) 埋深5 m地下管廊比埋深10 m的损伤概率略小，但相差不多。埋深36 m的盾构隧道的损伤概率明显比埋深10 m的大，更为危险。

(4) 大横截面地下管廊比小截面的损伤概率大，更为危险；大直径盾构隧道比小直径的损伤概率大，更为危险。