基于脉动法的上海市RC剪力墙结构基本自振周期测试与分析
闫培雷, 郭恩栋, 吴厚礼, 金宇航
(中国地震局工程力学研究所 中国地震局地震工程与工程震动重点实验室,哈尔滨 150080)
上海市高层建筑从20世纪80年代的121幢已经发展到如今的3万余幢[1],由于整体性好、侧移刚度大、承载力高等优点[2],剪力墙结构在30层以下的高层建筑中得到广泛应用,已成为上海市的主要建筑结构类型之一。作为人口财富密集型的超大城市,上海市面临着潜在巨大的地震和台风灾害风险。剪力墙结构在地震或台风作用下响应与破坏取决于结构动力特性和外部荷载特性。结构动力特性是建筑自身固有的特性,包括自振周期、振型和阻尼比等,其中基本自振周期是其中极重要的参数之一,用于估算结构承受的地震作用与风荷载。因此,确定结构基本自振周期对结构的抗震抗风设计、维修加固、安全性评估以及损伤识别具有十分重要的意义。
在我国,结构自振周期一般采用经验公式计算获得,经验公式法是对特定类型建筑进行大量动力性能测试,通过回归分析拟合给出基本自振周期经验公式[3-16]。相较于理论计算获得的基本自振周期,动力性能测试结果是建筑真实性态的反应,排除了各种假定的影响,如质量分布、材料实际性能、节点刚度、填充墙布置以及施工质量等,数据准确可靠。因此,经验公式法是一种用于快速估算结构动力特性的可靠方法。
在结构初始设计阶段,设计者多依据文献[17]中的经验公式估算剪力墙结构的基本自振周期。该公式是基于20世纪六七十年代在北京、上海、天津、广州、成都等十几个城市内80余栋高度在50 m以下的结构实测数据拟合而成的[18]。四十多年以来,随着我国钢筋混凝土结构的相关规范和标准逐步修订完善,剪力墙结构的抗震措施发生了显著变化,结构高度大多超过50 m,目前对于高度超过50 m钢筋混凝土剪力墙结构的动力特性的研究较少[19-20]。针对上述问题,本文通过对上海市已建成的62栋剪力墙结构进行动力性能测试,获得了结构水平纵横两个方向上的基本自振周期;采用其中的60栋结构的数据进行回归分析,分别给出了以高宽比和总高度为自变量的高度范围在45~90 m的基本自振周期的经验公式;并用2栋结构的数据验证了公式的可靠度。相较于文献[11]和[12],在参照文献[17]给出了基于高宽比的钢筋混凝土剪力墙结构基本自振周期经验公式的基础上,同时参考美国相关规范[21-23],给出了采用“幂次高度系数”形式的结构基本自振周期经验公式,该公式较我国现行规范中相关公式的形式更为简洁且自变量数量更少,本文给出的公式是对相关规范的补充和完善。
1 RC剪力墙结构的脉动测试及结果
1.1 测试结构的基本情况
本文对上海市的62栋RC剪力墙结构采用脉动法进行了结构动力性能测试。脉动法是利用自然环境对结构不规则的微弱干扰,不用任何激振设备,通过结构脉动响应来确定测试结构的动力特性,不会对测试结构造成损伤,也不影响其正常使用。
作为测试样本的RC剪力墙结构以住宅为主,平面布置基本规则对称且平面形状以矩形为主,竖向刚度基本均匀,结构总高度的分布如表1所示。
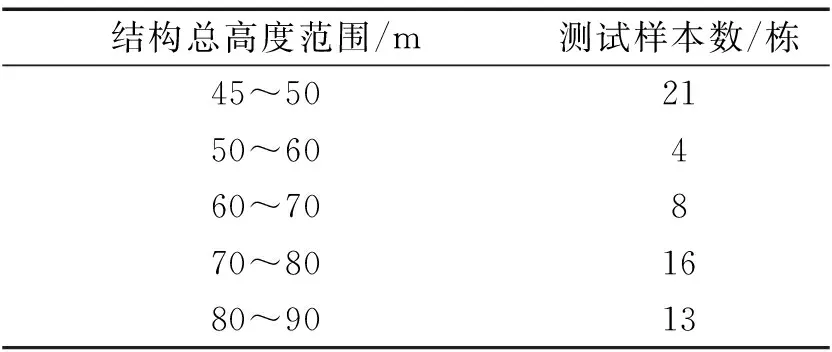
表1 不同总高度范围内测试样本数Tab.1 Number of test samples in different total height ranges
1.2 现场脉动测试流程与原则
脉动法测试采用G01NET-2通用数据采集器和941-B超低频测振仪(如图1所示)。G01NET-2是多通道数据同步高速采集仪,应用于结构测试中振动信号的采集、分析及处理。941-B型超低频测振仪是用于测量结构在环境激励下的低频脉动信号。

图1 脉动测试采用的仪器和设备Fig.1 Instruments and equipment for pulsation testing
为保证脉动测试数据准确可靠,现场测试过程中按照以下原则进行:
(1) 测试前搜集结构竣工图,确定结构总高度、长度、宽度和平面刚度中心;
(2) 测振仪应布置在结构平面刚度中心处的主要承重构件附近,且应沿水平双向布置,用于保证测振仪接收到的信号以平移振动信号为主,尽量减少扭转振动信号;
(3) 在结构顶层及一半高度处的楼层布置测振仪,不必层层布置测振仪;
(4) 单次测试时间至少保证5分钟以上;
(5) 确保每栋结构均设置2个测试位置,每个测位置分别测试3次,每次测试包含水平纵向和水平横向2组数据。
1.3 数据处理与结果
以上海市嘉定区曹安公路黄渡3#地块9号楼为例,将测试数据经过傅里叶变换得到自功率谱(如图2所示),进行阻尼识别后,通过结构自功率谱峰值可确定其水平方向上的基本自振频率,而基本自振周期为基本自振频率的倒数,可得一组数据下结构的基本自振周期(如图3所示),并将6组结果取平均值,给出结构在水平纵横两个方向上的基本自振周期。
图2 水平横向速度时程数据Fig.2 Velocity time history data in the horizontal direction
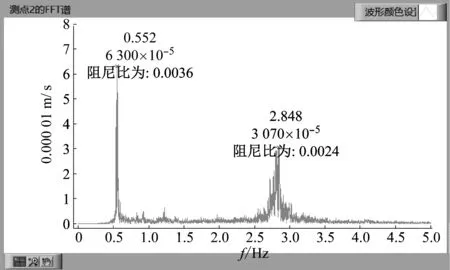
图3 水平横向自功率谱Fig.3 Power spectrum in the horizontal direction
按照上述处理方法,给出上海市62栋结构分别在水平纵横两个方向上的基本自振周期(如表2所示)。

表2 实测基本自振周期Tab.2 Measured fundamental natural period
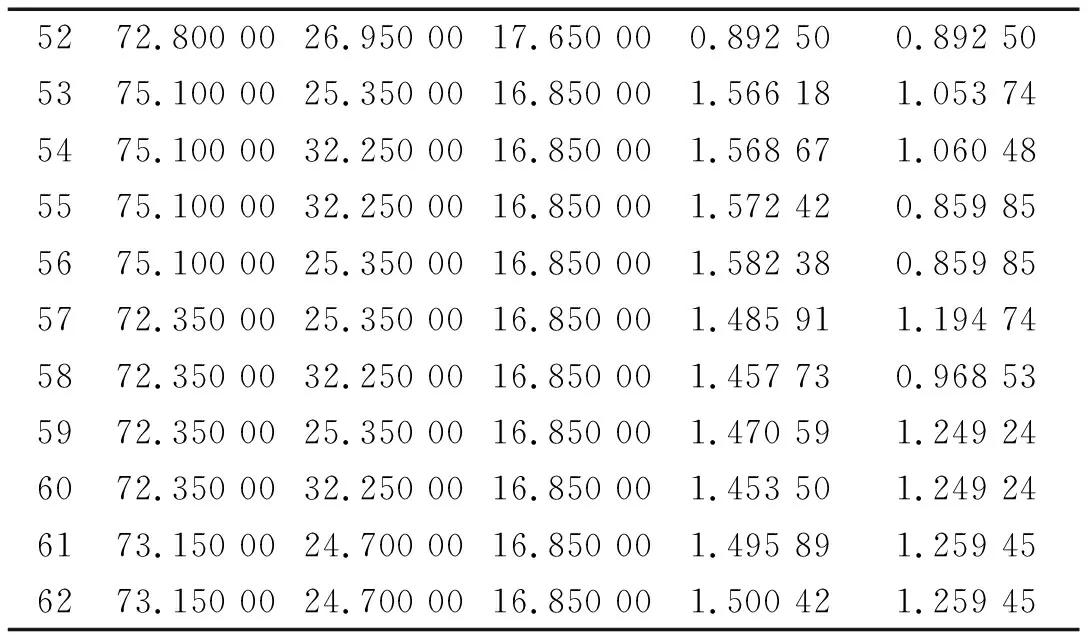
5272.800 0026.950 0017.650 000.892 500.892 50 5375.100 0025.350 0016.850 001.566 181.053 74 5475.100 0032.250 0016.850 001.568 671.060 48 5575.100 0032.250 0016.850 001.572 420.859 85 5675.100 0025.350 0016.850 001.582 380.859 85 5772.350 0025.350 0016.850 001.485 911.194 74 5872.350 0032.250 0016.850 001.457 730.968 53 5972.350 0025.350 0016.850 001.470 591.249 24 6072.350 0032.250 0016.850 001.453 501.249 24 6173.150 0024.700 0016.850 001.495 891.259 45 6273.150 0024.700 0016.850 001.500 421.259 45
2 RC剪力墙结构基本自振周期的回归分析
脉动实测值反映的是结构微小变形时的动力特性,其往往小于抗震设计中采用反应谱法时的基本自振周期。若按照实测数据统计基本自振周期分布规律,将导致水平地震作用增大。因此,需对实测基本自振周期值进行修正。文献[24]出自中国建筑科学研究院工程抗震研究所编制的《抗震验算与构造措施(86年设计规范背景资料、条文解说汇编) 》,其研究表明:针对RC剪力墙结构而言,用于统计回归基本自振周期的脉动实测值小于抗震分析时的周期值,一般需要进行修正并且取修正值为1.3。该参数被中国建筑科学研究院1984年编制的《工业与民用建筑抗震设计规范(TJ11-78)条文修改报告:筋混凝土框架及剪力墙房屋自振周期经验公式的建议》所收录,并于1987年被《建筑结构荷载(GBJ 9—1987)》正式采纳,一直沿用至《建筑结构荷载(GBJ 50009—2012)》。因此,取修正参数为1.3具有较好的可靠性。
2.1 结构水平横向
文献[17]中RC剪力墙结构基本自振周期经验公式如下所示
(1)
采用该公式的形式,以结构的总高度和宽度为自变量,以结构水平横向上的基本自振周期为自变量,基于SPSS22.0统计分析软件对60栋结构的水平横向基本自振周期进行回归分析,分析结果如图4所示。
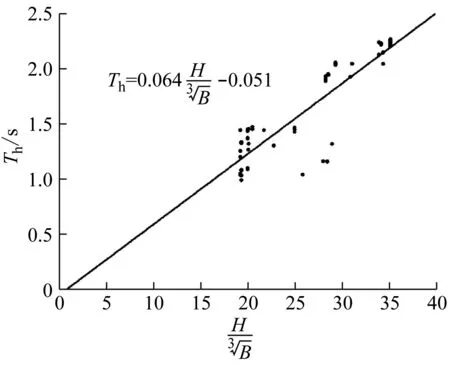
图4 基于结构总高度和宽度的横向基本自振周期经验公式Fig.4 Empirical formula of the horizontal fundamental natural period based on total height and width of structures
则结构水平横向上的基本自振周期经验公式为
(2)
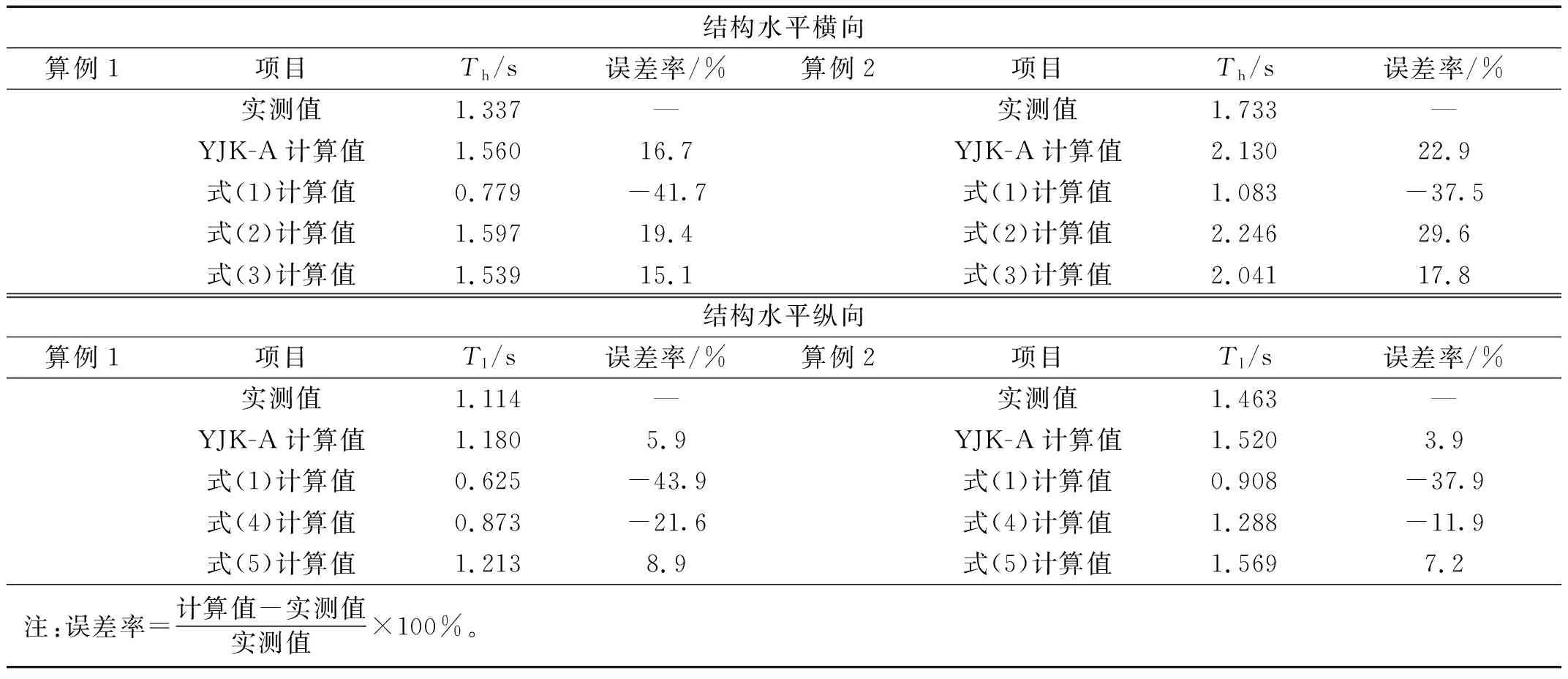
式中,45 m 美国相关规范中钢筋混凝土剪力墙结构的基本自振周期经验公式多采用“幂次高度系数”的形式,其系数是根据大量强震记录所得的数据拟合而成。因此,采用“幂次高度系数”的形式,以结构总高度为自变量,以水平横向上的基本自振周期为自变量,基于SPSS22.0统计分析软件对60栋结构的水平横向基本自振周期进行回归分析,分析结果如图5所示。 图5 基于结构总高度的横向基本自振周期经验公式Fig.5 Empirical formula of the horizontal fundamental natural period based on total height of structures 则结构水平横向上的基本自振周期经验公式为 Th=0.03H0.944 (3) 式中,45 m 决定系数,又称拟合优度,在统计学中用于度量因变量的变异中可由自变量解释部分所占的比例,以此来判断统计模型的解释程度。对比式(2)和式(3)发现,式(3)的决定系数高于式(2)的决定系数,说明在水平横向上,结构总高度对结构基本自振周期的影响比结构总高度和宽度的影响大。 采用文献[17]中的公式形式,以结构的总高度和长度为自变量,以结构水平纵向上的基本自振周期为自变量,基于SPSS22.0统计分析软件对60栋结构的水平纵向基本自振周期进行回归分析,分析结果如图6所示。 图6 基于结构总高度和长度的横向基本自振周期经验公式Fig.6 Empirical formula of the longitudinal fundamental natural period based on total height and length of structures 则结构水平纵向上的基本自振周期经验公式为 (4) 式中,45 m 采用“幂次高度系数”的形式,以结构总高度为自变量,以水平纵向上的基本自振周期为自变量,基于SPSS22.0统计分析软件对60栋结构的水平纵向基本自振周期进行回归分析,分析结果如图7所示。 图7 基于结构总高度的横向基本自振周期经验公式Fig.7 Empirical formula of the longitudinal fundamental natural period based on total height of structures 则结构水平横向上的基本自振周期经验公式为 Tl=0.033H0.864 (5) 式中,45 m 对比式(4)和式(5)发现,式(5)的决定系数略高于式(4)的决定系数,说明在水平纵向上,结构总高度和长度对结构基本自振周期的影响与仅有结构总高度的影响基本相当。 上述分析表明:在上海市的总高度在45~90 m之间的RC剪力墙结构,采用 “幂次高度系数”形式的基本自振周期经验公式的拟合优度好于采用文献[17]的形式的经验公式的拟合优度,且采用 “幂次高度系数”形式的基本自振周期经验公式的参数少形式简单。 选择两栋未参与回归分析的RC剪力墙结构的脉动测试数据,验证本文给出的结构在水平纵横两个方向上的基本自振周期经验公式(2)~(5)的准确性。 算例1为上海市长风11地块西北住宅项目6号楼,该结构用途为住宅,高度为64.8 m,长度为34.8 m,宽度为17.5 m,结构如图8所示。 算例2为上海金桥地铁保障房8号楼,该结构的用途为住宅,高度为87.4 m,长度为26.6 m,宽度为15.45 m,结构如图9所示。 从表3中可以看出: 表3 RC剪力墙结构基本自振周期值计算值与经验值对比Tab.3 Comparison of calculated value and empirical value of fundamental natural period of RC shear wall structure 式(1)给出的结构在水平纵横两个方向上的基本自振周期计算值均小于实测周期值,且计算误差率较大,导致结构初始设计阶段估算的水平地震作用偏大。 在结构水平横向上,式(2)式(3)给出的计算值均大于实测周期值,且式(3)的误差率小于式(2)的误差率;在结构水平纵向上,式(4)和式(5)给出的计算值均大于实测周期值,且式(5)的误差率小于式(4)的误差率;式(3)和式(5)的计算值更接近于有限元计算结果。上述分析表明,采用 “幂次高度系数”形式的经验公式的误差率较低。 基于上海市的 62栋高度在45~90 m的RC剪力墙结构动力性能测试数据,识别了结构在水平纵横两个方向上的基本自振周期并进行了回归分析。本文的主要结论如下: (1) 对于高度在45~90 m之间的RC剪力墙结构,结构总高度是影响结构基本自振周期的重要因素; (2) 针对高度在45~90 m之间的RC剪力墙结构,分别给出了基于结构高宽比和“幂次高度系数”的水平纵横两个方向上基本自振周期回归公式,通过两个实际工程验证了后者的拟合优度和误差率均优于前者,本文的研究是对现行规范中结构基本自振周期经验公式相关规定的补充; (3) RC剪力墙结构住宅的初始设计阶段,在已知结构信息较少的情况下可采用本文给出的式(3)和式(5)估算结构基本自振周期,用于初步估算结构承受的地震作用和风荷载。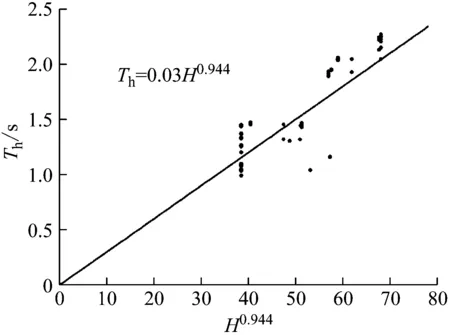
2.2 结构水平纵向
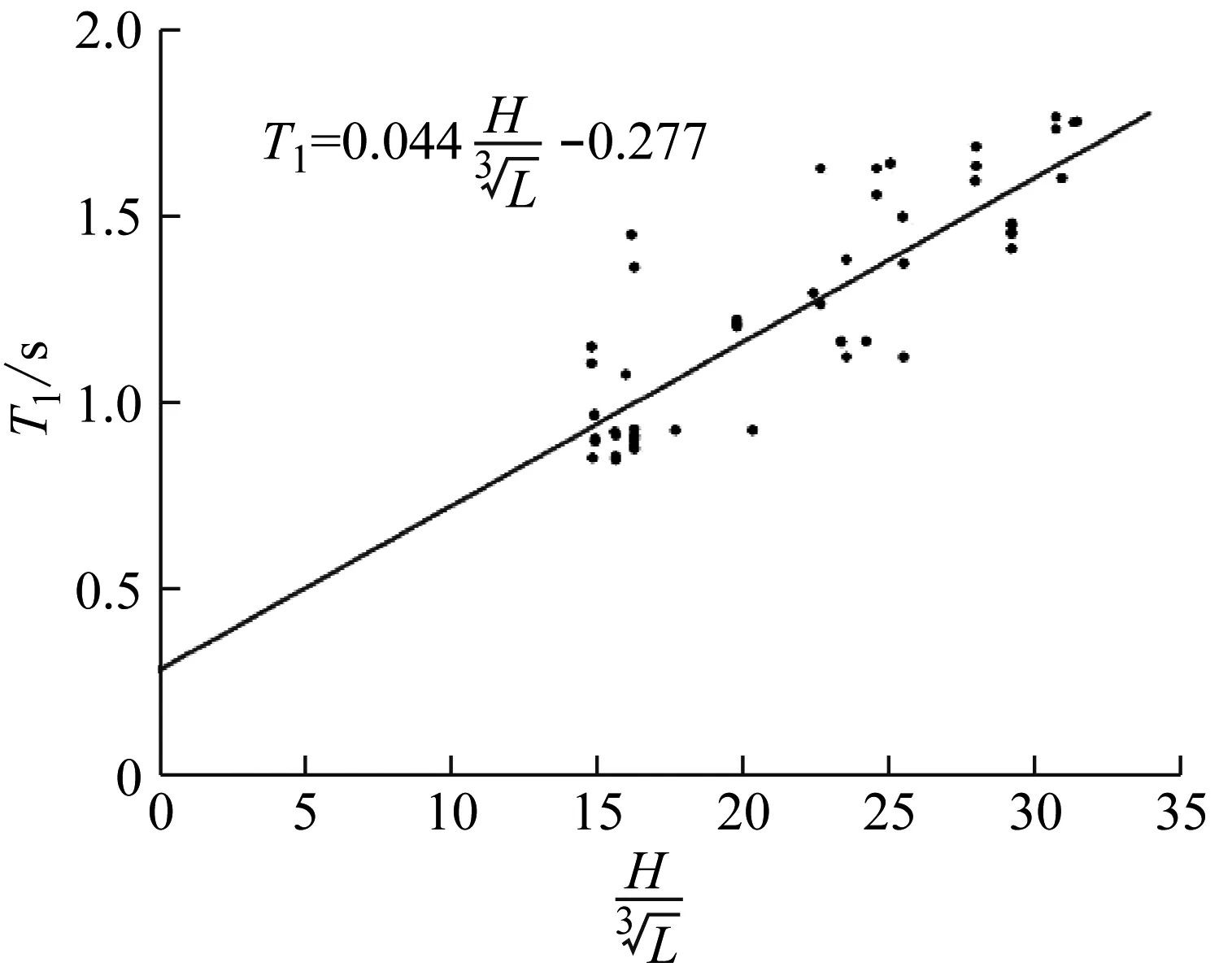
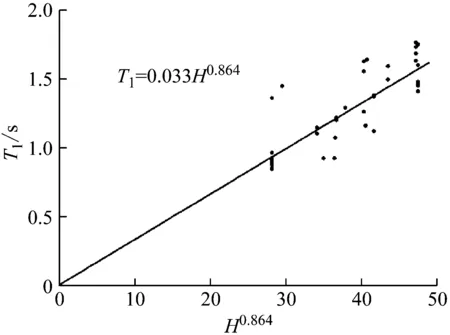
3 结构基本自振周期经验公式准确性验证
4 结 论

