基于位移频响函数灵敏度分析的模型修正

张亚峰， 殷 红， 彭珍瑞， 张雪萍， 董康立

(1.兰州交通大学 机电工程学院，兰州 730070；2.浙江大学 生物医学工程与仪器科学学院，杭州 310027)

基于灵敏度的有限元模型修正(finite element model updating，FEMU)是一种广泛应用于结构损伤识别的方法。FEMU可以表示为数值优化问题，通过最小化测量值和初始有限元值的差异，迭代求解模型未知参数[1]。近几十年来提出的大量模型修正方法中，基于模态参数和频响函数(frequency response function，FRF)的模型修正方法为主流方法。在基于模态参数的模型修正方法中，实测模态参数的不完备性和模态分析误差可能会对模型修正产生显著的影响[2]，与其相比，基于FRF的模型修正方法具有以下优点[3-4]：避免了模态识别过程中的误差；测量数据的不完备性对基于FRF的模型修正方法影响较小；FRF中包含的结构数据信息多于模态参数中包含的结构信息；FRF具有互易性，在一点得到的数据可以通过另一点验证，因此，这些数据具有更高的可信度。

基于FRF灵敏度的FEMU方法，虽然有大量的数据可以利用，但实际的模型修正中仅有少量的数据得到利用。因此在利用FRF进行有限元模型修正时，FRF灵敏度方程的建立和频率点及频率段的选择显然是非常重要的问题[5]。总之，利用FRF灵敏度进行FEMU仍然有很多问题值得研究。童宗鹏等[6]由结构的数值计算和试验测试得到的频响函数，给出两者的相关函数及其灵敏度的表达形式，提出了一种模型修正方法；战家旺等[7]提出了一种基于FRF模式置信准则的改进模型修正方法，用以识别各部位的损伤指数，从而对简支梁的损伤进行定量评估；Petersen等[8]针对大型土木工程结构的数值模型容易出现误差和系统参数不确定性的情况，研究了有限元模型修正中的灵敏度方法；Machado等[9]研究了基于FRF灵敏度的模型修正法估计桥梁材料参数的随机特性。灵敏度分析法是基于振动试验数据修正工程结构有限元模型众多方法中最成功的方法之一，已经成功地应用于大规模的工业问题[10]，然而，基于灵敏度分析法的模型修正很难直接迭代得到正确的收敛结果，所以传统灵敏度分析法中应用加权法和正则化技术等。

本文在建立FRF灵敏度方程时引入新的中间设计参数，有效地避免了加权和正则化的应用，并且研究了如何选择包含尽可能多信息的一个频率点。此外，FRF有限元模型修正结果也受到激励点和测点位置的影响，所以选择了合理的激励点和测点的位置，从而缩小灵敏度方程的数量。最后通过对经典三自由度系统和二维桁架结构设定损伤来验证该模型修正方法的有效性。

1 基于频响函数灵敏度的模型修正方法

1.1 传统频响函数灵敏度分析的模型修正

利用单位矩阵：

Z(ω)H(ω)=I

(1)

式中:Z(ω)为刚度函数；H(ω)为位移FRF。对设计参数求偏导

(2)

式中:pi为待修正参数。对于某一个特定的频率ωk，利用一阶泰勒展开式，可以得到灵敏度方程：

(3)

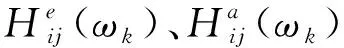
(4)

(5)

将式(3)扩展到整个系统，则有：

{ε}=[S]{Δp}

(6)

式中:{ε}为nf×1的FRF试验值与理论值的残差向量；[S]为nf×np灵敏度矩阵；{Δp}为np×1待修正参数的改变量;nf为从参考数据中利用的频率点数目;np为需要修正的参数数目。如果试验中采用nj个激励点和ni个响应点，则灵敏度矩阵将会变成(nj×ni×nf)×np的矩阵。求解{Δp}

{Δp}=[S]+{ε}

(7)

式中:[S]+=[STS]-1ST，经过迭代求解，有限元模型新的参数为

{p}new={p}old+{Δp}

(8)

这种传统灵敏度方法限制在只能成功应用于初始有限元模型与试验模型接近的模型。尽管选择合理的修正频率范围和实现灵敏度方程的数值平衡可以有效改善解的准确性和收敛性，但依然不能克服这些基本限制。

1.2 改进频响函数灵敏度分析的模型修正

在建立FRF灵敏度方程时，为了将FRF灵敏度分析方法的适用范围引用到更常见的实际模型修正和损伤识别中，需要引入新的设计变量将非线性问题转化为线性问题。

Lin[11]提出了一种新的FRF灵敏度分析方法，研究得到一般结构动态系统中FRF灵敏度随参数的变化可以表达成如下形式

(9)

在本文中，式(9)参数Δpi为改变量，将其范围扩大为负的初始值到正的初始值。通过优选单激励点和测点来计算并拟合在优选频率点时的灵敏度函数曲线，可以求解得到常系数ai和bi。另外考虑到建立有限元模型的精度直接受到结构横截面积的影响，所以需要对轴向刚度进行修正和损伤识别。由此改变和定义新的设计参数

(10)

将式(6)转变成如下形式

(11)

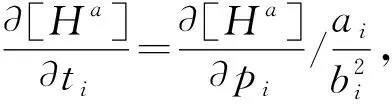
Δti=ti(Δpi)-ti(0)

(12)

从式(12)中求解{Δp}，代入式(8)可得有限元模型新的参数。

2 模型修正激励点和测点选择

模态试验中激励点或测点选择不当会影响有限元模型分析结果和试验结果的相关性分析。针对激励点和测点的选取问题，采用模态参与变异系数准则[12]选取激励点位置，频率响应有效独立法(frequency effective independence, FEFI)[13]结合距离系数-有效独立法[14]选取测点位置。

2.1 激励点选择

模态参与可以评价不同的激励点对于激发结构各阶模态的效果，模态参与变异系数准则正是在模态参与的基础上提出的。模态参与的公式如下

i=1，2，…,N0r=1,2,…,nr

(13)

式中:i为测点；j为激励点；r为模态阶数；nr为所关心模态的阶数；N0为测点总数；Aijr为留数；Wjr的值为第j个激励点对于激发第r阶模态的效果，该值越大，效果越好。基于模态参与准则，引入一个新的判据

(14)

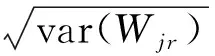
(15)

式中:φir，φjr分别为模态矩阵中的第(i,r)和(j,r)项；ωr为第r阶共振频率；ξr为第r阶模态阻尼比，此时，式(13)中的留数可表示为

Aijr=φirφjr

(16)

将式(16)代入式(13)得

(17)

将式(17)代入式(14)得

(18)

Vj值最小的激励点是单输入模态试验中的最佳激励点。

2.2 测点选择

采用FEFI选择测点位置，主要步骤如下：

(1) 在目标频率范围内，利用有限元分析得到的结构固有频率和振型计算频响数据矩阵

D=[H(ω1)H(ω2)H(ω3)…H(ωnf)]

(19)

式中,H(ωk)∈Cni×nj为频率ωk(k=1,2,…,nf)处的频响矩阵。

(2) 对FRF数据进行主成分分析，可以通过奇异值分解将D表示为

D=USV

(20)

式中:U为一个ni×ni维的复正交矩阵，它相互正交的列向量称为主方向；S为由奇异值组成的对角矩阵；V为一个nj×nj维的复正交矩阵，它的行向量表示相应主方向上归一化的频率响应。频响矩阵的各主方向同时满足

DD*=US2U*

(21)

式中:上标*为共轭转置。奇异值的大小反映了系统的总能量在相应主方向上的分布，因此，根据奇异值的大小保留D的主分量，使保留的奇异值和主方向所对应的能量占到系统总能量的95%～99%。频率响应通常可以由数量相对较少的主方向来重构。

设U=[u1,u2,…,uni]，V=[v1,v2,…,vnj]T，S=diag(σ1,σ2,…,σr,…,0)。其中，ui∈Cni×1，σi是D的奇异值，若选前l个分量进行重构，则H可近似表示为

(22)

式中:DD为D的主分量。

(3) 通过主成分分析，从U中保留的主方向组成的矩阵记为ψ，频响数据矩阵可以表示为

(23)

Q=ψ*ψ

(24)

本文选择信息矩阵的行列式作为目标范数，计算有效独立分布向量

ED=diag(ψ[ψ*ψ]-1ψ*)

(25)

依次去除ED中最小元素对应的候选测点，直至候选测点数目为所需要的传感器数目。此外，采用FEFI选择测点时，若传感器数目大于目标模态数目，测点可能在局部聚集，导致信息冗余，因此还需采用距离系数-有效独立法，引入欧氏距离增加测点，直到布置的传感器采集的信息能够得到可靠的模型修正结果。

3 模型修正频率点选择

在实测的FRF中存在大量的采样频率点，而选择大量的频率点将耗费时间，且有些频率点是可信的，有些频率点是多余的。因此，选择恰当的频率点在有限元模型修正过程中尤为重要，能够提高正确的收敛性和精度。

首先试验模型和初始有限元模型同阶共振之间的频率段将不做考虑[15-16]，如图1所示。ωb将会增大迭代误差，因此排除ωb；其次靠近固有频率附近的频率点，由于基于导数的灵敏度关系精度较低，因此这类频率点必须从模型中排除。最后，利用FRF的相关性分析选择一个频率点。衡量FRF在频率段上的相关程度准则有模式置信准则(signature assurance criterion，SAC)和模式比例因子(cross signature scale factor，CSF)。SAC可以表示为

(26)

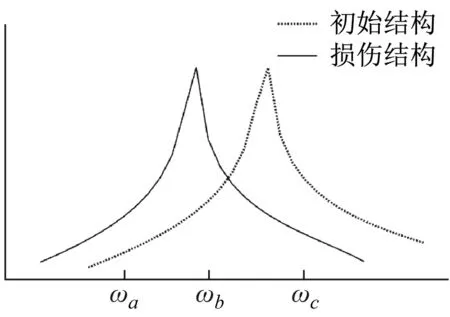
图1 结构在初始和损伤状态时第n阶固有频率附近的FRFFig.1 FRF near the nth natural frequency of the structure at the time of initial and damage

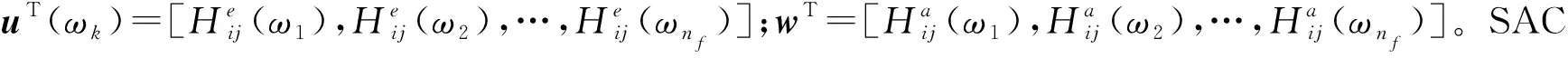
(27)

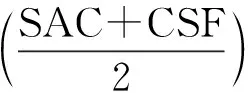
4 模型修正流程及步骤

基于以上理论绘制模型修正过程，如图2所示。具体步骤如下：

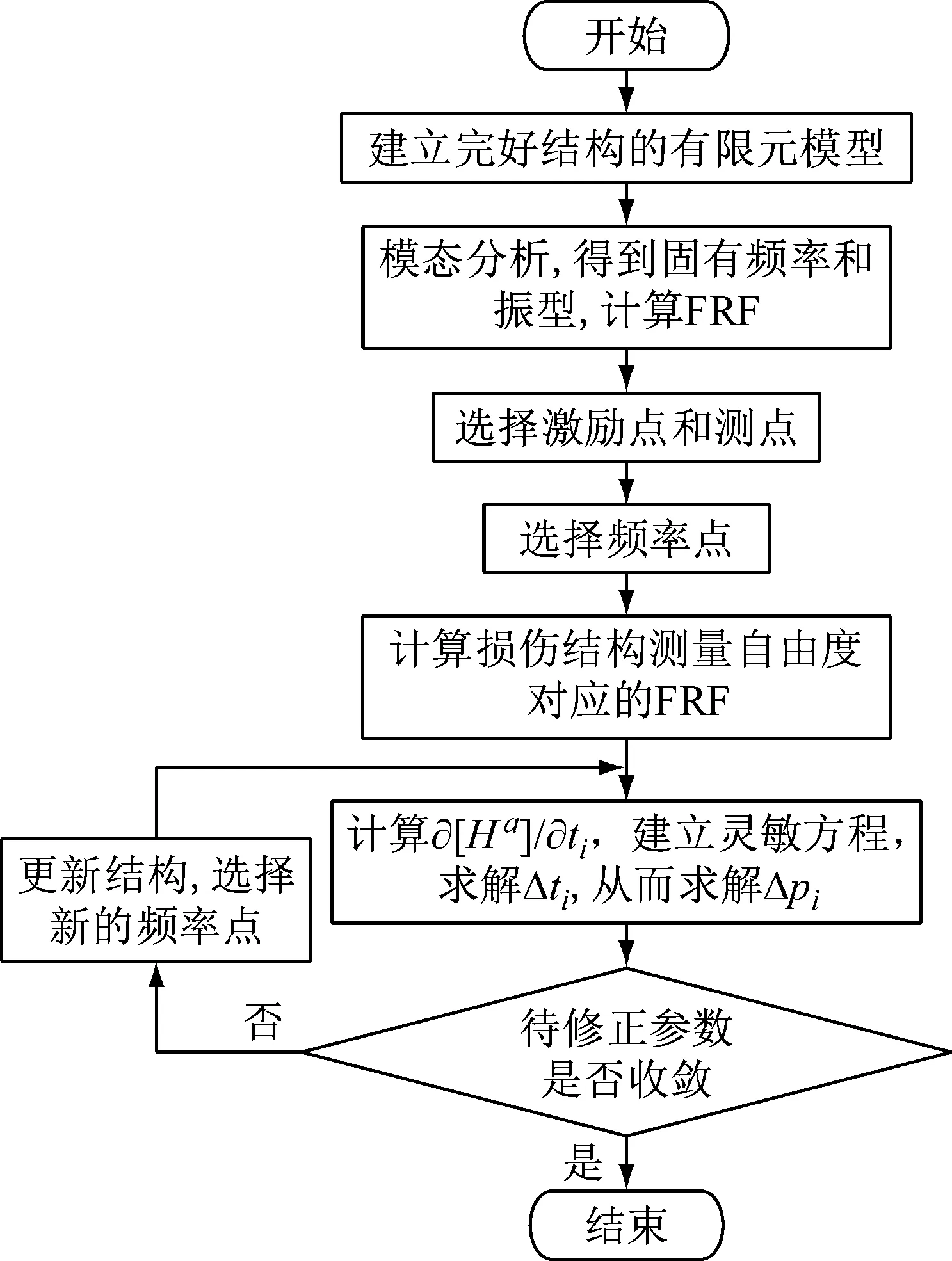
图2 模型修正流程图Fig.2 Model updating flow chart

(1) 根据式(18)选择一个最佳激励点，并利用所述测点选择方法确定传感器数量和测量位置，对建立的初始有限元结构模型进行模态分析并计算FRF。

(2) 结合FRF相关程度选择包含更多信息的一个频率点用来建立FRF灵敏度方程，并计算损伤结构测量自由度对应的FRF。

(3) 根据式(9)，利用步骤(1)中已选择的一个最佳激励点和其中一个测点来计算并拟合在步骤(2)中已选择频率点时的灵敏度函数曲线，引入中间设计参数，建立中间设计参数的FRF灵敏度方程组，通过先求解中间设计参数的改变量，再求解修正参数的改变量，经过迭代计算，最终确定损伤位置和程度。

5 数值模型试验

5.1 三自由度系统

三自由度系统，如图3所示。初始模型中的参数有m1=2 kg，m2=2 kg，m3=5 kg，k1=95 000 N/m，k2=90 000 N/m，k3=60 000 N/m，k4=60 000 N/m，k5=80 000 N/m，k6=70 000 N/m。将k1，k2和k5分别下降到75 000 N/m，70 000 N/m和60 000 N/m进行有限元分析，获得损伤结构的固有频率和FRF作为仿真的测试数据，并加入5%的随机高斯白噪声。

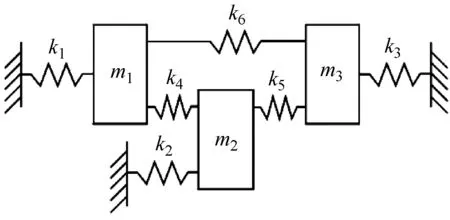
图3 三自由度质量-弹簧系统Fig.3 Three degrees of freedom mass-spring system

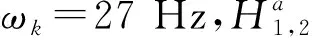
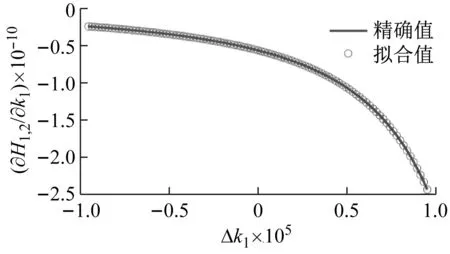
图4 频响函数灵敏度Fig.4 FRF sensitivity

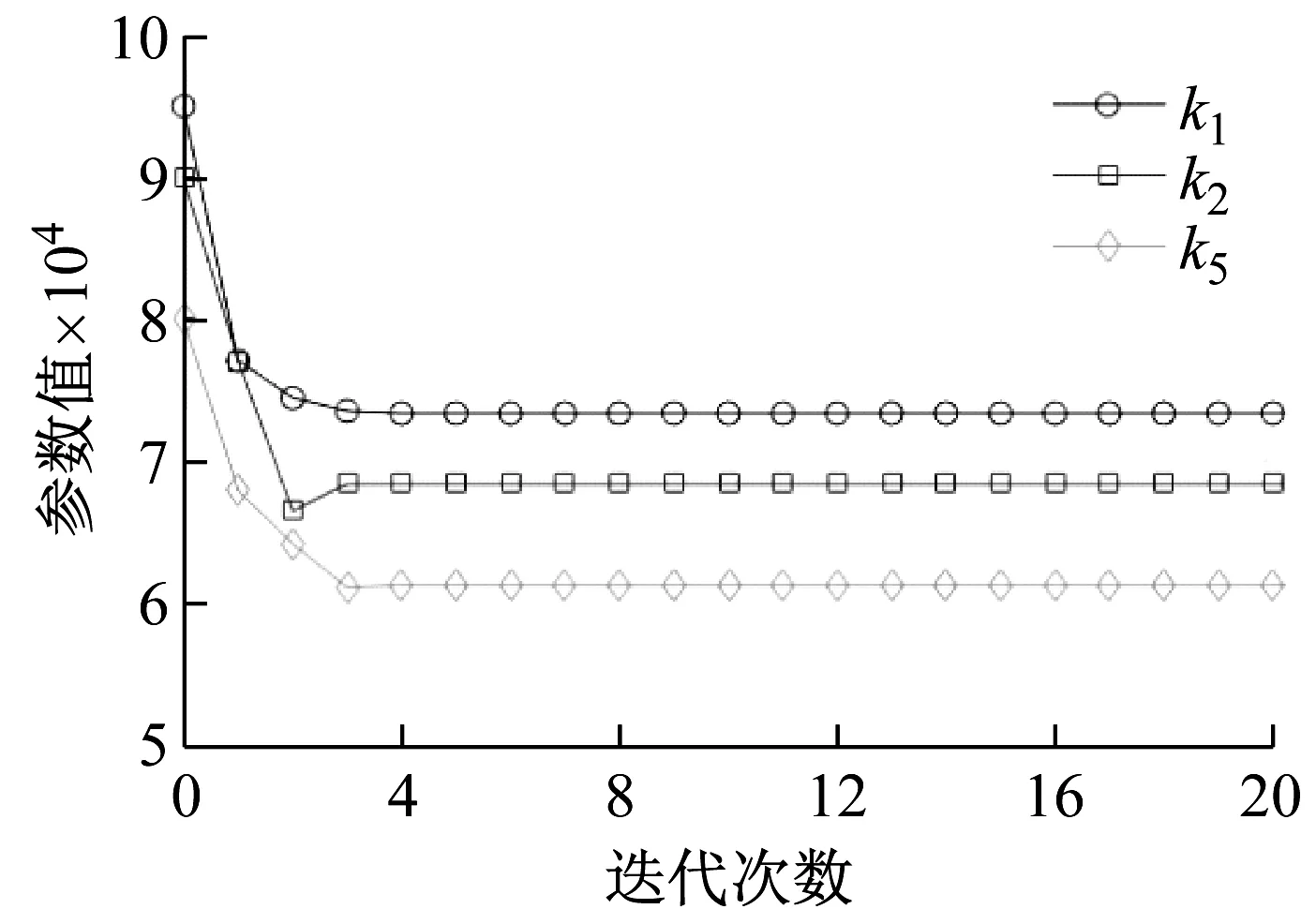
图5 参数迭代收敛情况Fig.5 Iterative convergence of parameters

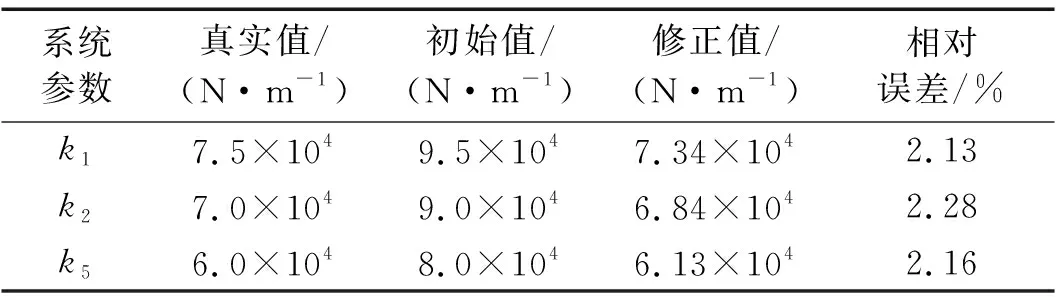
表1 刚度修正结果Tab.1 Updating results of stiffness

5.2 平面桁架结构

平面桁架结构,如图6所示。该桁架模型由36个杆单元组成，共有16个节点和29个自由度。所有杆单元的弹性模量为200 GPa，密度为7 800 kg/m3，单元横截面积为1 cm2，箭头表示激励。

图6 二维桁架结构Fig.6 Two dimensional truss structure

选择单元轴向刚度EA作为待修正参数，E、A分别表示杆的弹性模量、横截面积。为了模拟实际钢架结构中的阻尼，采用0.5%的阻尼比加入试验模型获得仿真试验数据。设定三种损伤工况来验证所提模型修正方法的有效性，在工况1中，预设第4、9、11、19、24和35杆单元为损伤单元，其刚度都下降30%；在工况2中，预设第3、13、18、21、26和32杆单元为损伤单元，其刚度分别下降15%、20%、5%、10%、30%和25%；工况3中，预设第12、17、22和29杆单元为损伤单元，轴向刚度分别下降30%、20%、5%和40%。使用以上数据进行有限元分析，获得损伤结构的固有频率和FRF作为仿真的测试数据。图7给出了工况1下第8自由度激励和第24自由度测量时结构在完好和损伤状态的无阻尼频响函数曲线。

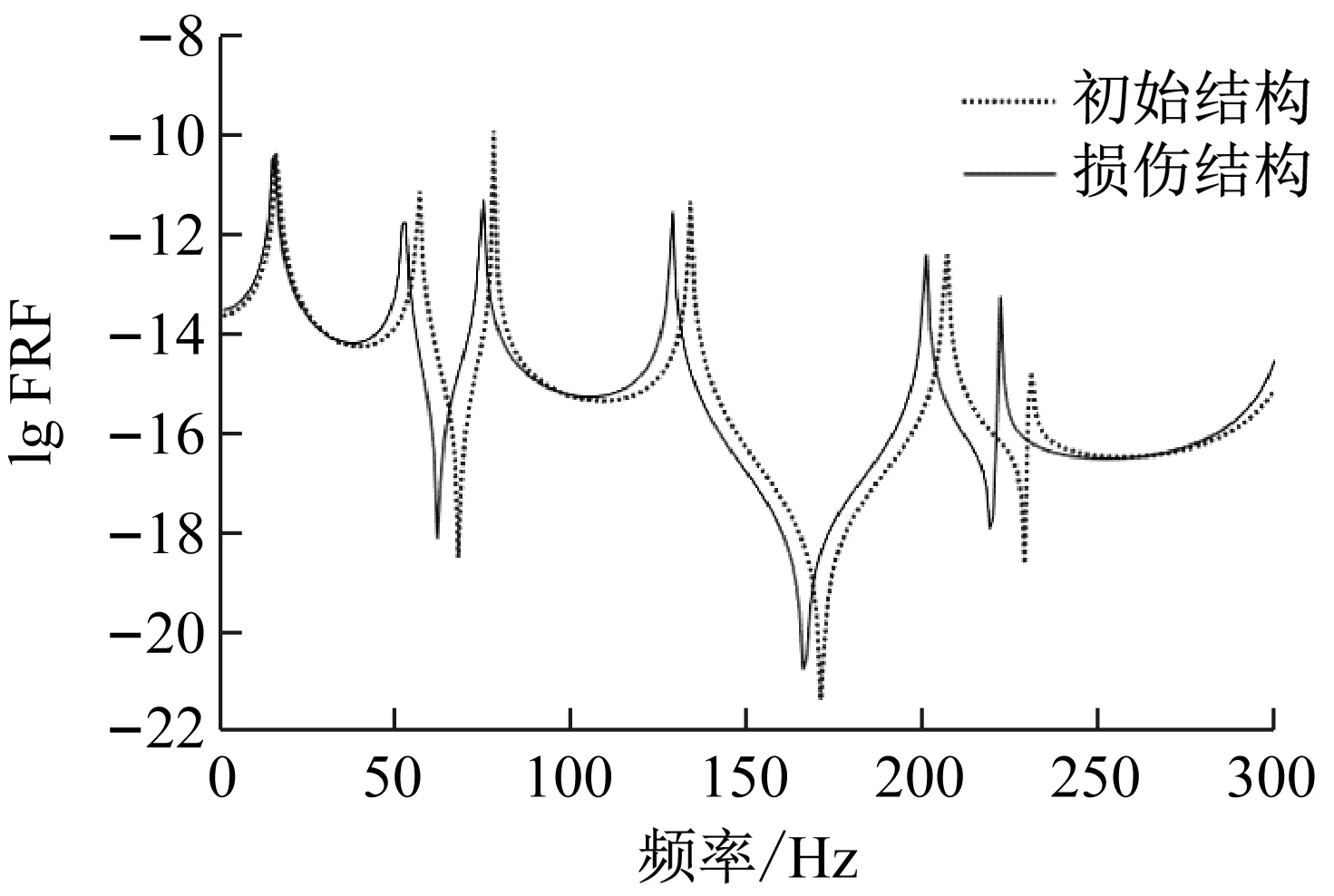
图7 初始和损伤结构对应的FRF(工况1)

Fig.7 FRF corresponding to the initial model and undamped damage at condition one

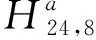
假设结构受到单点激励，选择激励点第2、8、14、16、24和29自由度处。经过5次迭代，损伤工况1、2和3的损伤识别效果如图9所示。从图9(b)和图9(c)可知，结构发生不同的损伤位置和程度都可以准确地识别出结构损伤位置和程度。结构发生损伤的单元，参数修正结果如表2所示。修正后损伤单元轴向刚度趋近于真实值，在损伤工况1、工况2和工况3中修正值和真实值之间最大的相对误差仅为0.636%。可见，模型修正的参数识别结果与损伤结构真实值高度吻合。而结构未发生损伤的单元，通过模型修正会预测微小程度的损伤，这是因为存在阻尼的影响。

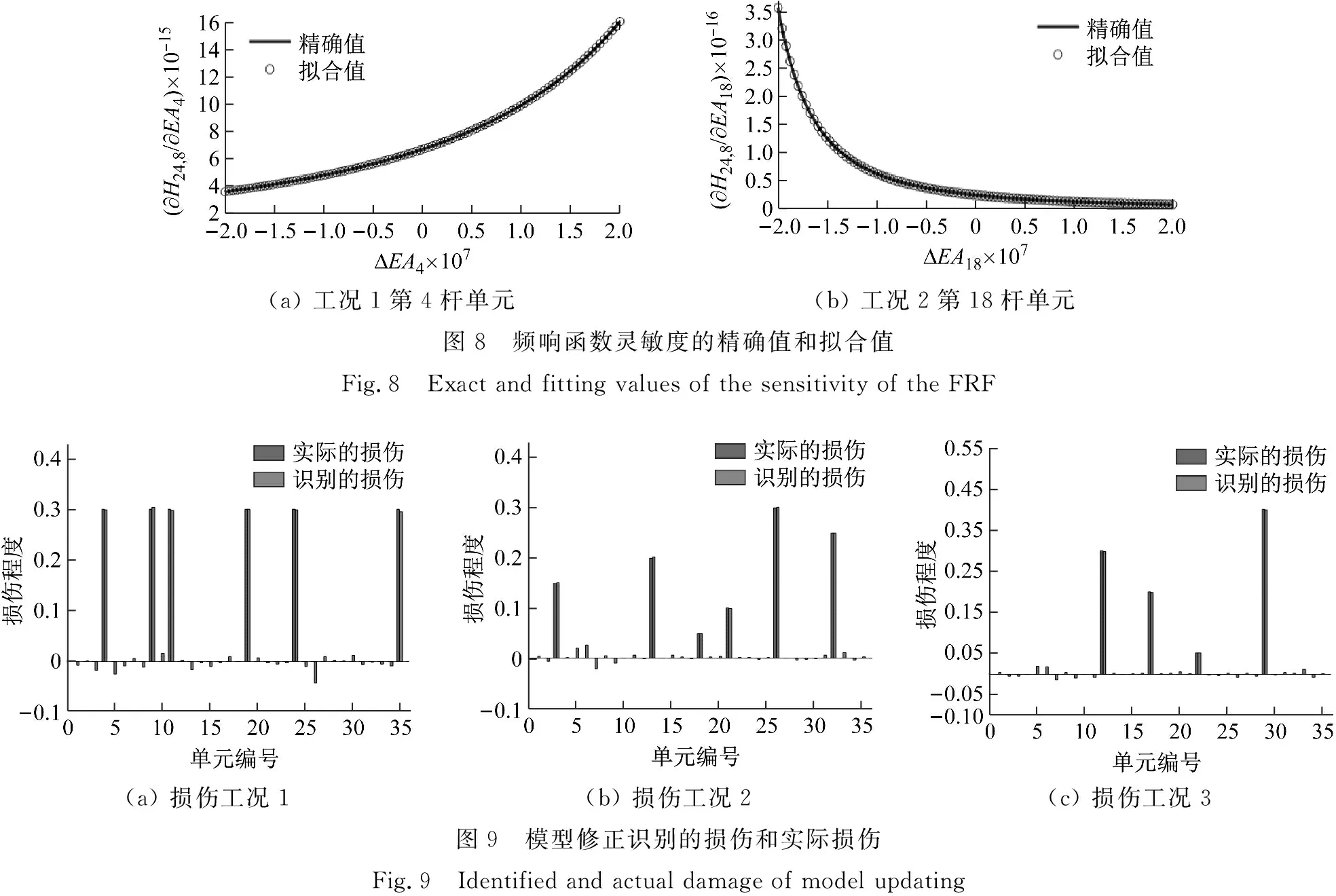
表2 三种损伤工况下轴向刚度EA修正结果Tab.2 Updating results of axial stiffness EA under three damage conditions

将上述已选测点中第16自由度改选为第18自由度，损伤工况1的识别效果如图10所示。从图10可知,杆11的参数修正结果误差明显增大，且在无损伤杆单元出现错误识别，具体修正结果如表3所示。若再将已选测点中第28自由度改选为第26自由度，损伤位置和程度甚至无法识别。综上，表明了本文所选测点方法的合理性。

图10 工况1模型修正识别的损伤和实际损伤Fig.10 Identified and actual damage of model updating at condition one

表3 工况1刚度的修正结果Tab.3 Updating results of stiffness in condition one

6 结 论

(1) 所提模型修正方法在传统FRF灵敏度分析方法的基础上，引入新的中间设计参数可以将非线性问题转化线性问题。结果表明，能够准确识别损伤位置和程度，并且从误差值可以看到，损伤识别精度较高和对于随机噪声具有鲁棒性，有较好的工程应用潜力。

(2) 相比传统灵敏度分析方法，本文建立的频响函数灵敏度方程组明显达到了数值平衡的效果，因此不需要加权和正则化技术，并且在迭代计算中能够快速收敛，具有良好的稳定性。

(3) 合理确定用于模型修正中包含更多信息的一个频率点，并且采用FEFI结合距离系数-有效独立法为模型修正选择较少测点位置，大量减少了FRF灵敏度方程的数量，提高了计算效率。