探讨导数计算时ΔX是不是0的问题

摘  要：微积分从诞生之初就因为无穷小量（?x）到底是不是0的问题，产生过纠纷，被贝克莱大主教攻击，从而引发了数学史上第二次危机。直到极限的提出和严格定义，才基本解决了这一问题。该文通过定义一个完整的计算过程中，所有的0大小都相等，所有的无穷小量大小都相等，也就是说，在计算过程中，0也是有大小的，0加0应该等于2个0，0减0应该等于0个0，它们和0也就是1个0都是不同的，保证了所有的0大小一致，就可以得到0/0=1。然后从导数定义和微积分基本定理出发，通过完善四则混合运算，在0做除数的时候，采用除法优先的原则，证明了某些连续函数上的尖点也有导数，从另一角度探讨了导数计算时?x是不是0的问题。

关键词：0可以做除数  除法优先  一一对应  导数的重新定义  0除以0等于1

中图分类号：O13                           文献标识码：A文章编号：1672-3791（2021）05（b）-0230-03

Abstract： Since the beginning of the birth of calculus， because of the infinite small quantity （?x） is zero or not in the end， there has been a dispute， was attacked by the Archbishop of Berkeley， which led to the second crisis in the history of mathematics. It was not until the limit was put forward and strictly defined that the problem was basically solved. In this paper， by defining a complete computation， all zeros are equal in magnitude， all infinitesimal quantities are equal in magnitude， that is， in the computation， 0 also has magnitude， 0 plus 0 should be equal to two 0's， 0 minus 0 should be equal to zero 0's， they are not the same as 0， that is， one 0.I make sure that all zeros are the same size， and I get it. Then， starting from the definition of derivative and the fundamental theorem of calculus， by improving the four mixed operations， when 0 is the divisor， using the principle of division first， it is proved that some of the sharp points on continuous functions also have derivatives， from another point of view， the problem of ?x is not 0 when the derivative is calculated is discussed.

Key Words： 0 can be a divisor; Division is preferred; One to one correspondence; The redefinition of the derivative; 0 divided by 0 is 1

3  结语

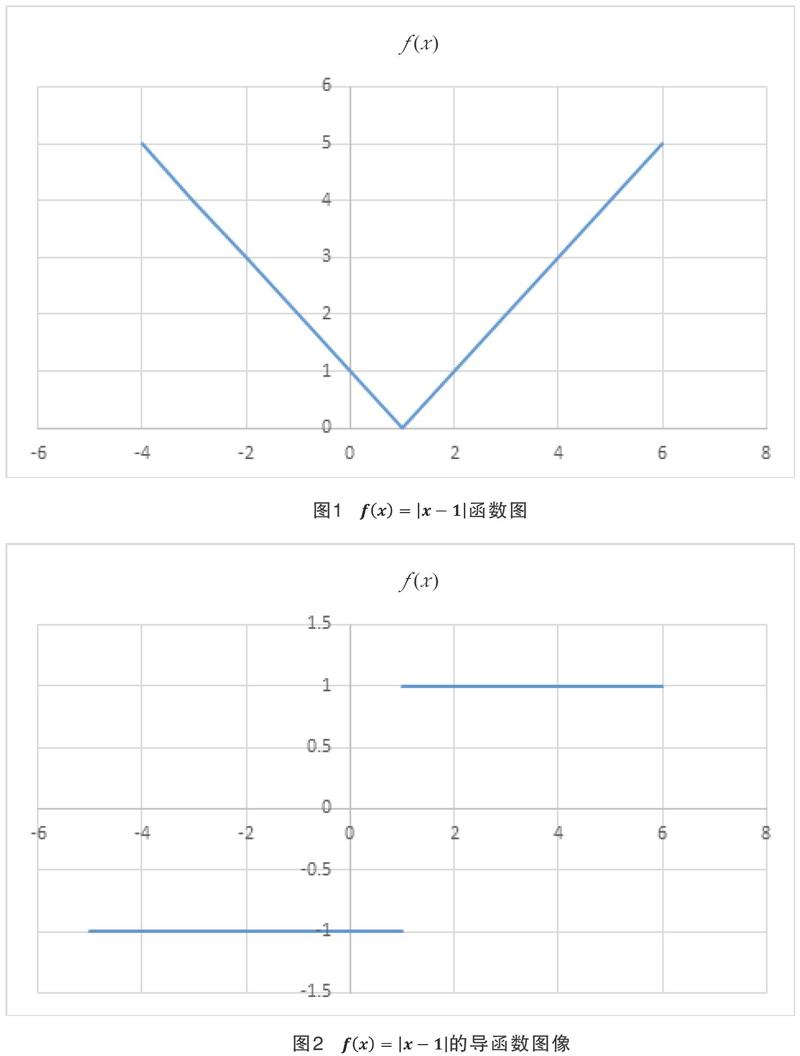
综上所述，连续函数在尖点处没有导数的结论是错误的，只不过是因为平滑处的导数不会因?x的取值而改变，而尖点处会改变。而导数计算中?x是不是0呢？该文认为应该是0，而不是一个无限趋近于0而不等于0的数，因为只有?x=0导数的值才具有唯一性，同时，像也只有在?x=0的情况下，才具备逻辑的严密性。

参考文献

[1] 羊应民.0做除数在现实中的意义[J].新智慧，2019（30）：62-63.

[2] 许高洁.函数的连续性与函数可导关系探讨[J].现代商贸工业，2019，40（10）：181-183.

[3] 潘阳.关于高等数学导数&不定积分计算方法探讨[J].吉林省教育学院学报，2018，34（11）：178-180.

[4] 姜金霞.分数阶微积分在流体流动传热及反常扩散领域的应用研究[D].北京建筑大学，2020.

[5] 周敬人.关于泰勒公式的应用探究[J].焦作大学学报，2020，34（4）：95-97.

[6] 张希.基于层次化模型的雷诺方程自适应变步长差分算法研究[D].武汉科技大学，2019.