复杂地形下C 波段雷达定量降水估计算法*

李 巧 戚友存, 朱自伟 杨 毅 闵锦忠 师春香 张 哲 李东欢 王 楠 胡启元

1.兰州大学大气科学学院，兰州，730000

2.中国科学院地理科学与资源研究所陆地水循环实验室，北京，100101

3.中国科学院大学，北京，100864

4.南京信息工程大学大气科学学院，南京，210044

5.国家气象信息中心气象数据研究室，北京，100081

6.陕西省气象局，西安，710014

1 引言

降水对气象、水文、地质灾害、农业畜牧业生产以及其他诸多科学和社会应用起着至关重要的作用，但是研发高精度、高时空分辨率降水预报产品具有极高的挑战性。众所周知，地面雨量站观测可以准确获取雨量计所在位置的降水量，但是基于地面雨量站观测的降水插值产品精度严重受到地面雨量站点的疏密和空间分布影响（沈艳等，2012；肖艳姣等，2011；Morrissey，et al，1995；Villarini，et al，2008）。在全球范围内，目前大部分地区地面雨量站的布设密度不足以捕捉到完整的中尺度系统引起的降水分布。对于经常诱发山洪地质灾害的对流尺度强降水，即便在发达国家，地面雨量计分布密度仍无法捕捉对流尺度强降水空间分布。静止气象卫星观测可以覆盖全球，时间分辨率也较高，但由于距离遥远，观测精度有一定的局限（高晓荣等，2013）。

为了弥补地面雨量计和卫星观测的不足，中国近20 年来布设了220 部CINRAD 天气雷达。目前中国雷达站网布设密集，多部雷达组网拼图可有效扩大雷达观测范围，因此，利用雷达资料进行定量降水估计（QPE）获取地面降水信息具有极大的优势（王红艳等，2009）。基于雷达扫描观测特征，天气雷达可以精确地捕捉地面降水的时、空分布。天气雷达最大观测半径可达450 km，并且，单雷达的空间分辨率可以达到1 km×1 km，时间分辨率可达5 min（Zhang，et al，2011，2016）。然而，雷达定量降水估计存在雷达固有的观测特征、反演技术和空间地理等方面的问题，包括地形、建筑物和地物的遮挡，降水粒子垂直方向的不均匀，降水粒子滴谱空间分布不确定等（Zhang，et al，2010，2011，2016；Qi，et al，2013a，2013b）。本研究主要从雷达探测资料质量控制、降水类型分类、雷达波波束遮挡，Z-R关系和雷达拼图5 个方面来提高雷达定量估计降水的精度。

天气雷达接收的回波信号除了气象回波，还包括地物回波、电磁干扰回波等非气象回波，这些非气象回波会严重影响雷达定量估计降水的精度。因此，在应用雷达资料前，需对其进行质量控制，剔除非气象回波，以提高定量降水估计精度。早期很多学者对雷达探测资料质量控制算法开展了大量研究工作，根据降水的时、空连续性，提出通过检查雷达回波的空间和时间连续性（Smith，1990），分析反射率因子的水平梯度和垂直梯度（Mueller，1977），对雷达探测资料进行质量控制，很大程度上去除了雷达非气象回波。近些年，很多学者利用概率分析方法进行雷达探测资料质量控制，以去除雷达非气象回波。Kessinger 等（2003）提出了采用模糊逻辑算法的雷达回波分类技术，从雷达资料（回波强度、径向速度和速度谱宽）中提取特征场，用于区分降水回波、地物和海浪回波等不同类型的雷达回波。刘黎平等（2007）基于Kessinger 等（2003）的模糊逻辑算法，提出了分步式识别地物回波的方法，对SA波段雷达进行了质量控制，改进了地物回波识别的效果。江源（2013）在已有的模糊逻辑算法识别地物回波基础上，引入人工智能识别方法，有效剔除了电磁干扰回波。本研究主要利用已有的模糊逻辑质量控制算法（江源，2013），对C 波段雷达进行非气象回波识别及去除，以提高雷达定量降水估计精度。

在雷达扫描平面内，若地形复杂，雷达电磁波波束会受到遮挡，这就会给雷达定量降水估计引入误差。为了去除地形遮挡导致的雷达定量降水估计的低估误差，学者（Fulton，et al，1998；Smith，1998）提出了根据雷达不同方位角波束遮挡情况，选择雷达复合平面扫描方法进行定量降水估计。雷达复合平面扫描方法已经业务应用于美国雷达定量降水估计系统（NMQ，Zhang，et al，2011），有效提高了雷达监测降水的能力，提高了雷达定量估测降水的精度。肖艳姣等（2008）将雷达复合平面扫描方法引入到中国S 波段雷达定量降水估计中，较大程度上提高了雷达定量降水估测的精度。本研究在已有研究基础上，基于陕西C 波段雷达研发雷达复合平面扫描技术，以解决低仰角雷达电磁波受到遮挡的问题。

基于计算得到的混合仰角反射率因子（以下简称混合仰角反射率），如何反演得到准确的降水率是雷达定量降水估计要解决的关键问题。目前雷达定量降水估计最常用的反演方法是基于单一雷达气象方程Z-R关系法（张培昌等，2001）来计算降水率。但本质上，降水率是由降水粒子滴谱决定的。Rosenfeld 等（2003）研究了不同区域、不同类型的降水，通过对降水粒子滴谱数据统计分析得到200 多种不同的Z-R关系，这说明单一的Z-R关系难以准确描述由于降水过程、降水类型和地区不同导致的降水滴谱特征差异，针对降水粒子滴谱特征不同使用相应的Z-R关系对于提高雷达定量降水估计的准确性具有重要意义。实际情况是，同一个雷达扫描平面内观测到的降水信息可能来自不同的降水类型，使用单一的Z-R关系会给雷达定量降水估计引入偏高或偏低的误差（Balakrishnan，et al，1989；Lee，et al，2006）。因此，需要针对不同类型降水采用不同的Z-R关系将雷达反射率转换成降水率，以提高雷达定量估计降水精度。文中基于雷达观测提供的体扫数据，结合不同类型降水的水平和垂直结构特征，研发降水类型分类模块，识别出不同类型降水。针对不同的降水类型选用具有代表性的Z-R关系将反射率转换成降水率，以提高雷达定量降水估计精度。

由于单部雷达定量降水估计受到雷达本身探测能力的限制，并且雷达波束随径向距离增大而升高，导致径向距离越远，观测信息对于地面降水的代表性往往越低。利用多部雷达降水观测信息进行相互补充，可以提供比单部雷达降水观测范围更广、精度更高的观测信息。因此，需要通过拼图的方式把多部雷达的降水观测信息组合到一起。目前，针对雷达拼图算法已经开展了很多研究，可以总结为以下两种方式：（1）先用单部雷达估测降水，再进行雷达组网拼图（Tabary，2007；高晓荣等，2012）；（2）基于雷达反射率场拼图，然后进行降水估测（肖艳姣等，2008；Zhang，et al，2011）。文中将先用单部雷达观测资料进行降水估测，然后再对单雷达降水估测场进行拼图。相较于高晓荣等（2012）的方法，文中基于降水结构及降水粒子垂直相态变化特征，确定单雷达在拼图时的权重系数，最终将单雷达观测的降水信息高效地组合到一起。

文中将从雷达探测资料质量控制、降水类型分类、雷达混合仰角反射率计算、Z-R转换关系和雷达拼图5 个方面介绍C 波段雷达定量降水估计方面的研究工作，最后通过对比地面雨量站降水观测产品，定量评估新开发C 波段雷达定量降水估计算法的性能。

2 雷达定量降水估计算法

选取陕西省为研究区域（图1）。陕西省地势南北高、中间低。北部为黄土高原，平均海拔1000 m左右，占全省面积的40%。中部为关中平原，平均海拔500 m 左右。南部为秦巴山区，包括秦岭-大巴山脉以及汉江谷地，平均海拔1500 m 以上。高原、山地、平原和盆地等多种地形错综复杂，降水导致的滑坡、泥石流等地质灾害经常发生。因此，提高定量降水估计产品的精度对于陕西省气象地质灾害的预警、防灾和减灾都具有重要意义。

所用降水量数据为陕西地面雨量站1 h 降水观测数据，陕西省西安、延安、榆林、安康、商洛、宝鸡、汉中7 部C 波段天气雷达原始体扫数据。图1a给出了陕西省的地形空间分布以及7 部C 波段天气雷达和地面雨量站的分布情况。基于地形空间分布，结合雷达扫描特征，可以计算出每部天气雷达的最大有效探测降水距离，图1b 给出了7 部雷达探测降水的最大有效距离。7 部雷达从北到南依次为榆林、延安、宝鸡、西安、商洛、汉中、安康。陕西省C 波段雷达波束径向探测距离为400 km，径向分辨率为500 m，方位角分辨率及波束宽度均为1°。体扫模式为VCP21，即一个体扫包括9 个仰角的扫描，仰角分别为0.5°、1.45°、2.4°、3.35°、4.3°、6°、9.9°、14.6°、19.5°，完成一次体扫的时间大约是6 min。7 部C 波段天气雷达和地面雨量站基本可覆盖全省。

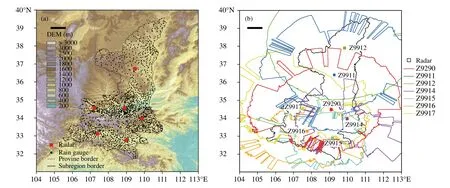
图1 陕西省（a）雷达站、地面雨量站和地形空间分布及（b）各雷达有效探测范围Fig.1 （a）Distribution of radars，surface rain gauge station，and topography in Shaanxi Province；（b）effective detection range of each radar in Shaanxi Province

雷达定量降水估计算法包括以下5 个相对独立的模块，图2 给出C 波段天气雷达定量降水估计算法流程，主要包括：（1）雷达探测资料质量控制，（2）雷达降水类型划分，（3）雷达混合仰角反射率计算，（4）Z-R关系统计分析，（5）雷达拼图。

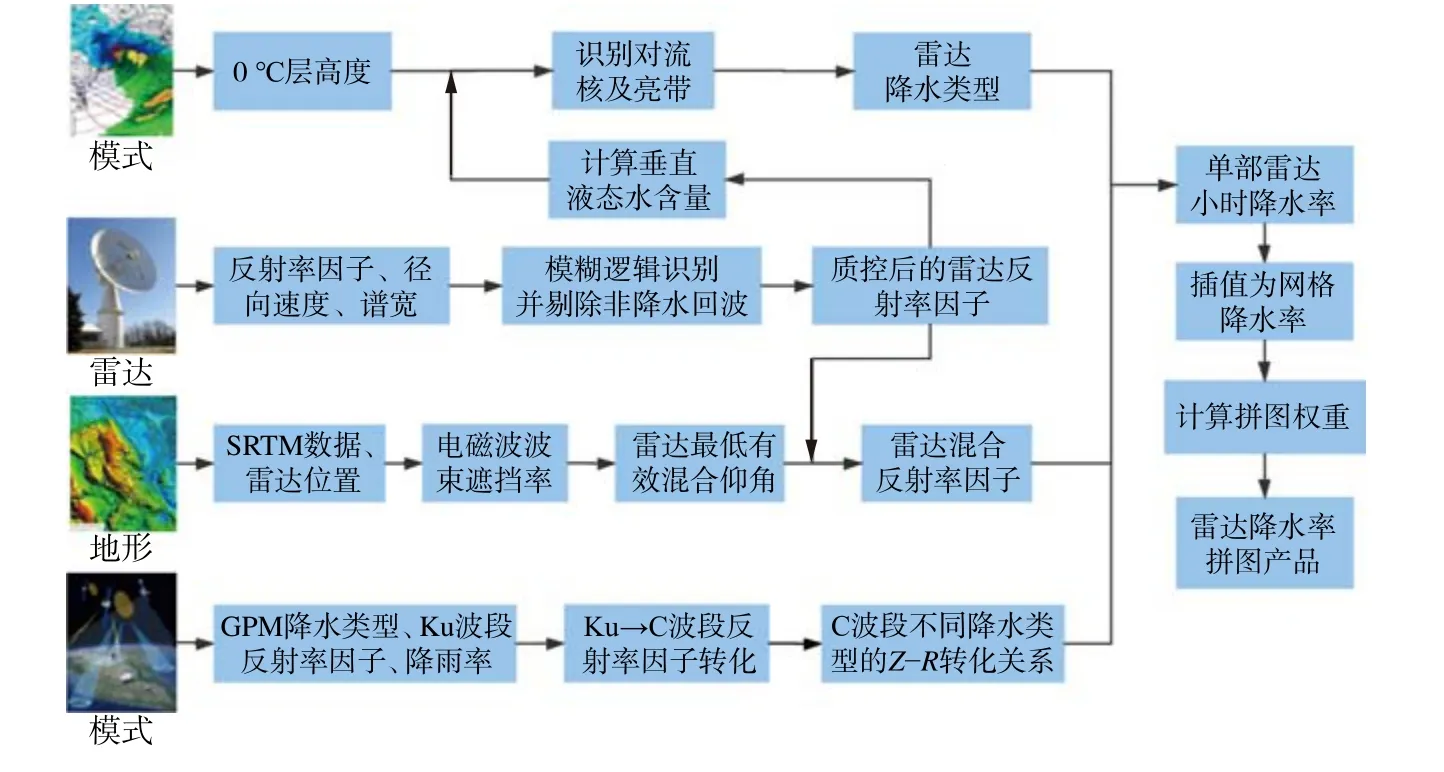
图2 雷达定量降水估计算法流程Fig.2 An overview flowchart of radar QPE algorithm

2.1 雷达探测资料质量控制

地物、晴空回波和海浪回波会影响雷达反射率因子数据质量，从而影响雷达定量降水估计精度，并导致风暴监测或跟踪失败。因此，雷达反射率因子数据在应用之前，有必要对其进行质量控制。对雷达基数据采用刘黎平等（2007）提出的模糊逻辑分布式地物回波识别方法对地物进行识别和剔除。模糊逻辑方法是区分降水回波、地物回波、晴空回波和海浪回波等物理量，然后根据这些回波的特征建立隶属函数（刘黎平等，2007），对这些物理量进行特征值计算，得到所有物理量对于不同类型回波的0—1 取值范围的判据。回波点物理量对应的判据值越大，那么该回波点属于该类型回波的可能性越大。对这些判据值进行加权累加，如果回波点的地物回波判据超过事先设定的阈值，那么，该回波点的回波将被识别成地物回波。具体计算方法与Kessinger 等（2003）的方法相同，首先，计算反映地物和降水回波差异的4 个物理量：（1）回波强度纹理（TdBZ），（2）回波垂直变化（GdBZ），（3）回波沿径向变号（SIGN），（4）回波沿径向变化程度（SPIN）。其次，计算反映地物和降水差异的径向速度和谱宽的3 个物理量：（1）径向速度的区域平均值（MDVE），（2）径向速度的方差（SDVE），（3）速度谱宽的区域平均值（MDSW）。这些物理量的具体定义见刘黎平等（2007）。

图3 给出了2019 年4 月28 日03 时24 分（世界时，下同）质量控制前（图3a）、后（图3b）西安雷达0.5°仰角反射率。从图3a 可以看到，在雷达附近有明显的地物回波，在40°左右有明显的尖峰（spike），质量控制之后（图3b），这些地物回波和尖峰基本被准确识别出来，降水区域的信息基本保留。结果表明：该方法对地物回波和降水回波区分效果较好，多数地物回波能够被有效滤除，甚至某些距离模糊区，速度不可用的位置，地物也被识别出来。需要注意的是，在降水系统边缘，部分气象回波较弱，被误识别为非气象回波从而被滤除。

图3 2019 年4 月28 日03 时24 分西安雷达0.5°仰角反射率回波（a.质量控制前，b.质量控制后）Fig.3 Reflectivity of Xi'an radar（a）before and（b）after QC at 0.5° elevation at 03：24 UTC 28 April 2019

2.2 雷达降水类型分类

雷达降水类型分类算法基于单雷达体扫降水观测资料，自动识别降水类型，本研究中将降水类型分为对流性降水（简称CV），不受0°C 层亮带影响的层状云降水（简称ST）和受0°C 层亮带影响的层状云降水（简称BB）。降水类型识别是提高雷达定量降水估计精度的重要前提之一，正确的降水分类使得定量降水估计时可以针对不同降水类型引入更具代表性的Z-R关系，以有效提高定量降水估计的精度。

降水类型分类模块主要是利用质量控制后的雷达反射率数据，对不同降水类型进行识别，得到降水类型产品。

2.2.1 0°C 层高度检查

在进行对流核识别前，先检查0°C 层高度，该信息可从模式数据或探空资料获取。文中应用的二维0°C 层高度数据从美国国家环境预报中心的全球预报系统（GFS）GFS-ANL 资料中获取，该资料空间分辨率为1°×1°，时间分辨率 为6 h。当0°C 层高度过低（低于雷达高度2 km），则认为没有对流产生，这样的设定是基于如果地面温度较低，对流不容易产生的前提，避免了把低高度的0°C 层亮带误识别为对流而造成定量降水估计高估的现象。

2.2.2 对流核识别

对流核识别算法是基于单雷达体扫数据，在极坐标下实现。算法考虑了地面雷达探测的特性，在不同区域采用不同的判据来识别对流核。识别对流核基于多个仰角的反射率和垂直液态水含量等，避免了由于仅判断特定层次的反射率或者组合反射率（用体积扫描获取的回波强度数据，在每个方位-斜距库上，对所有仰角的反射率因子在垂直方向进行比较，挑选出最大的反射率因子）而把强0°C 层亮带误识别为对流核的问题，具体算法详见Qi 等（2013b）和Zhang 等（2021）。

2.2.3 对流区识别

在识别出所有对流核之后，采用区域增长方法来识别整个对流区。区域增长方法通过检查对流核格点四周的8 个格点，如果这8 个格点中的任何一个格点满足下述特定条件，则将其标记为对流区，并以其为新的对流核继续检查其邻近的8 个格点，直到所有的对流核都被检查完毕。在检查完所有格点后，满足条件的格点即为算法识别出的对流区。

降水类型分类算法中综合组合反射率、最大反射率高度、反射率垂直梯度这3 个物理量进一步判断识别出的对流区是否正确。如果该格点组合反射率超过35 dBz 且满足下面条件之一，则判断该格点为对流：（1）组合反射率大于45 dBz（0℃层亮带反射率一般不超过45 dBz），（2）最大反射率高度不在0℃层亮带影响的高度（说明高反射率值不是由于融化效应所导致的），（3）反射率垂直梯度小于4 dBz/km（对流在垂直方向上相对均匀，反射率垂直梯度较小）。

2.2.4 0℃层亮带区识别

在识别出整个对流区之后，其余非对流降水区域即为层状云降水区，层状云降水区存在0℃层亮带型和非0℃层亮带型降水。0℃层亮带识别算法将首先识别0℃层亮带核，即在层状云区中雷达组合反射率超过35 dBz 的格点。然后，通过区域增长法，基于0℃层亮带核识别出整个0℃层亮带区，该区域定义为从最高仰角接触到0℃层高度的位置到最低仰角接触到0℃层高度的位置，区域增长法的判定条件为组合反射率超过30 dBz。

图4 给出了雷达组合反射率（图4a）和对应的降水类型分类结果（图4b）。可以看到，该算法很好地将飑线和飑线后方的强0℃层亮带区识别出来，而在雷达北部的小范围对流区也被识别出来，即降水类型分类算法能够较好地识别对流性降水，0℃层亮带型层云降水和非0℃层亮带层状云降水。

2.3 雷达混合仰角反射率计算

在利用雷达反射率进行定量降水估计时，当雷达探测到的信息离地面越近，对于地面真实的降水强度描述就越具备代表性，故使用最贴近地面的雷达仰角观测反射率信息进行降水估计更为准确。然而在实际操作中，低仰角在某些方位角上因受到地形遮挡而无法获得降水信息。为得到完整有效的降水信息，需要利用更高仰角的信息进行补充。

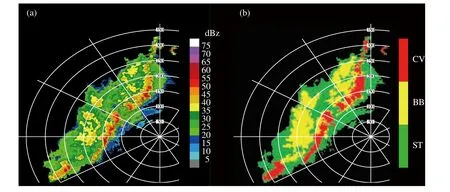
图4 （a）雷达组合反射率和（b）降水类型分类结果（CV、BB、ST 分别代表对流性降水、0℃层亮带层状云降水和非0℃层亮带层状云降水）Fig.4 （a）Composite reflectivity and（b）precipitation type（CV，BB，and ST stand for convective，bright band and stratiform，respectively）

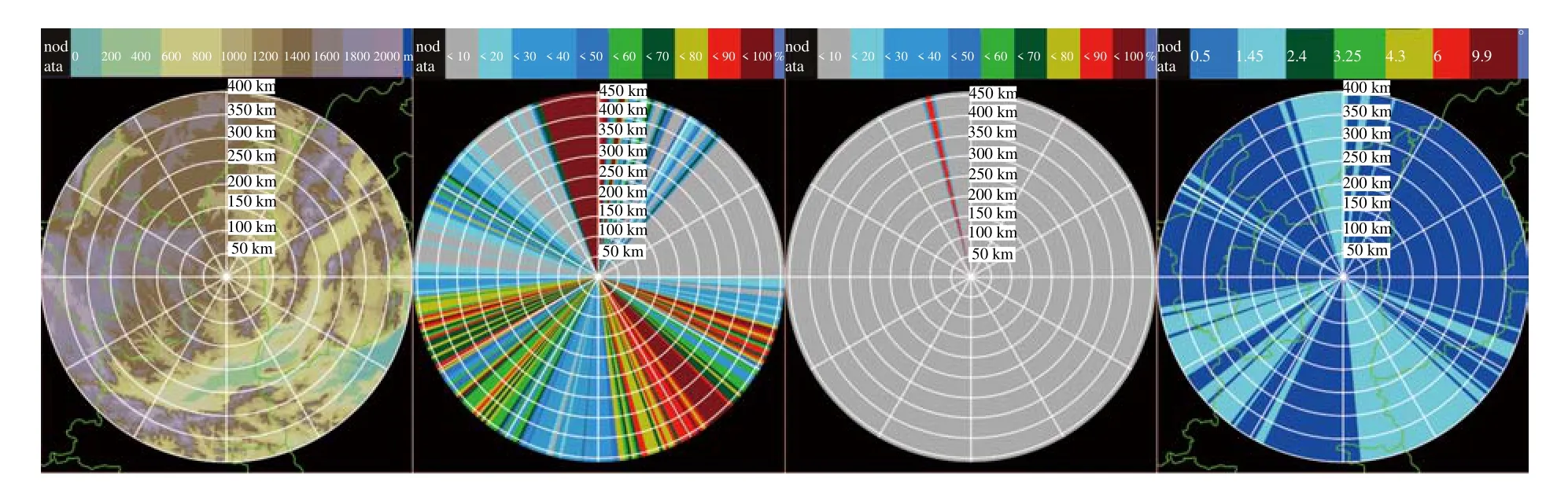
图5 延安雷达（a）扫描平面内地形空间分布及雷达（b）0.5°、（c）1.45°仰角电磁波遮挡百分比空间分布和（d）雷达混合仰角Fig.5 Distribution of（a）topography，electromagnetic wave shielding percentage at（b）0.5° elevation and（c）1.45°elevation，and（d）hybrid elevation angle of Yan'an radar

在雷达复合平面扫描中，高精度地形数据是美国航空航天局（NASA）和国防部国家测绘局（NIMA）联合测量的机载雷达地形探测任务（SRTM）数字高程模型（DEM），空间分辨率为30 m×30 m。雷达复合平面扫描方法主要是利用高精度地形数据，结合雷达探测原理，计算每部雷达电磁波遮挡百分比，从而得到每部雷达的有效最低混合仰角。计算雷达电磁波能量遮挡百分比，需要确定雷达电磁波在传播过程中，雷达波束对应位置的地形高度空间分布。假设雷达电磁波在标准大气中传播，基于等效地球半径模型（Langston，et al，2007 ；Zhang，et al，2005）可以得到

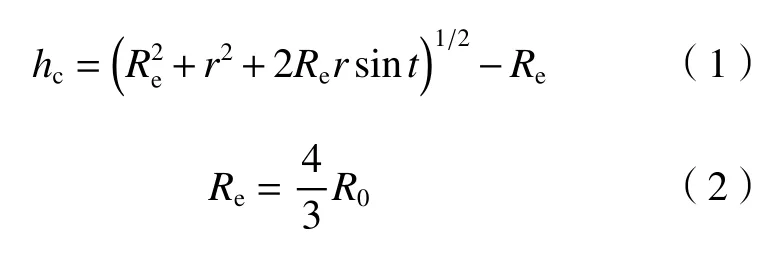
式中，hc为雷达电磁波波束中心相对于雷达站点的高度，r为电磁波的传播距离，R0为地球半径，Re为等效地球半径，t为雷达观测仰角。

此外，由于雷达波束随着传播距离的增大而变宽，设定波束宽度为 θ，则将式（1）中的t替换为可以分别得到波束顶部高度（ht）和波束底部高度（hb），而任意径向距离上波束的垂直（与波束正交方向）截面直径（d）可以表示为

根据雷达电磁波能量在垂直截面上满足高斯分布，并结合SRTM 数字高程模型计算

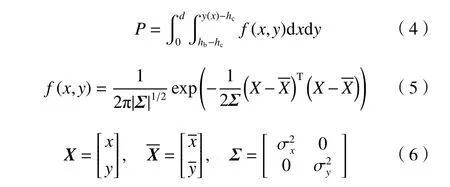
式中，P为雷达电磁波能量遮挡百分比，x是电磁波垂直截面上距离波束中心的水平距离，y(x)为相对于电磁波波束底部的地表高程，f(x,y)为高斯分布函数，标准差。

当地形对雷达电磁波能量遮挡超过50% 时，认为雷达电磁波受地形遮挡严重，雷达观测的降水信息缺失严重。此时，依次查看高层仰角在相同方位角、相同径向距离上的能量遮挡百分比，找到地形对雷达电磁波能量遮挡小于50%的最低仰角，即为雷达在该方位角和径向距离上的最低有效仰角。同时，对于最低有效仰角上的反射率，按照能量遮挡百分比进行能量补偿。由于雷达平面内地形的遮挡情况分布可能不一致，不同位置对应的最低有效仰角可能不同，因此将最低有效仰角在雷达平面上的分布称为最低有效混合仰角，在最低有效混合仰角上得到的反射率数据称为混合仰角反射率。

图5 给出了延安雷达的地形空间分布（图5a），雷达0.5°仰角（图5b）、1.45°仰角（图5c）的电磁波遮挡百分比空间分布以及得到的雷达混合仰角产品（图5d）。从图中可以看出，延安雷达周围地形复杂，在0.5°仰角，雷达西南、东南、西北偏北方向电磁波均受到严重遮挡，而在1.45°仰角，雷达仅在西北方向受到部分遮挡，根据雷达在不同仰角不同方位角的地形遮挡情况生成的混合仰角则综合了各个方位角的最优反射率情况，可以较全面地获得降水信息。

2.4 基于GPM 星载双频雷达（DPR）观测统计分析Z-R 关系

Zhu 等（2020a，2020b）利用全球降水测量任务（GPM）星载双频雷达（DPR）对陕西省降水时、空变化特征的分析得到了以下结论：（1）不同降水类型的垂直结构（微物理过程）具有明显的差异，（2）相同降水类型和强度的垂直反射率廓线在陕西省不同季节和不同地区的差异并不显著。因此，利用GPM 卫星雷达反演的滴谱数据对不同降水类型的Z-R关系进行了统计分析，文中所用GPM 卫星数据从地球数据网站（https://storm.pps.eosdis.nasa.gov/storm/）获取。

在利用卫星雷达的近地面反射率和降雨率进行Z-R关系拟合之前，需要将卫星雷达Ku 波段的反射率转换为与地面雷达相同频段（C 波段）的反射率（Zhu，et al，2020b），这样形成的Z-R关系才能直接应用于地面雷达的定量降水估计。雷达的反射率可以用以下公式表示（Zhang，et al，2001）

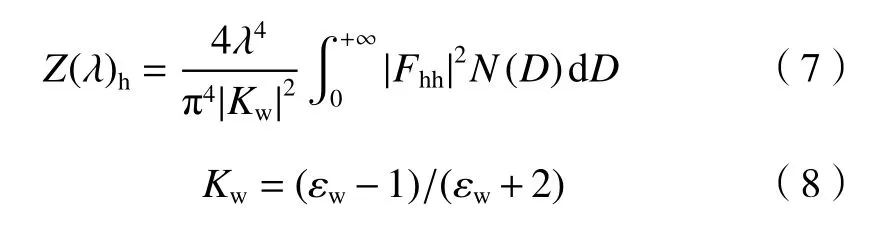
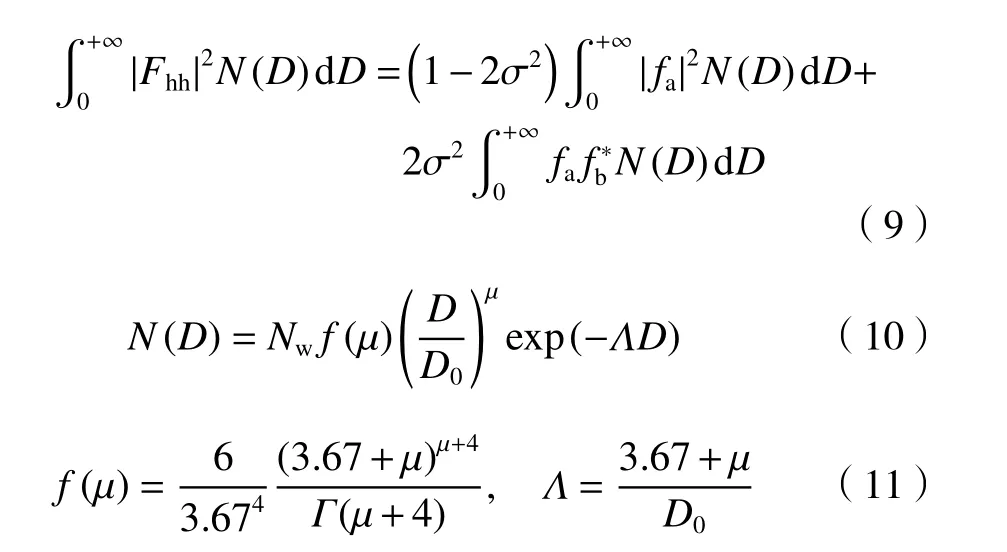
式中，Z(λ)h是雷达水平方向的反射率，λ是电磁波波长，Kw是介电系数，εw是液态水的介电常数，|Fhh|2为水平偏振散射振幅的二阶矩，σ为倾斜角（雨滴下落过程中雨滴长轴与垂直方向的夹角）的标准差，fa为电磁波后向散射在长半轴的振幅（复数），为电磁波后向散射在短半轴的振幅实部，可通过T-Matrix（Mishchenko，et al，1996；Mishchenko，2000）方法计算，N(D)是雨滴谱，Nw是归一化浓度参数，D是粒子直径，D0是粒子中值直径，µ是形状参数，Λ是斜率参数，Γ（*）是伽马函数。

通过改变式（10）中滴谱参数 (µ,D0,Nw)的取值（µ取−1—4，D0取0.5—2.5 mm，Nw取103—105），计算C 波段和Ku 波段反射率差值（DFR），其变化关系如图6a 所示。总的来说，C 波段和Ku 波段的反射率差值在雨区为负值，即由Ku 波段转换为C 波段后，反射率减小。随着D0的增大，DFR 呈先略微增加后减小再增大的特征，两次变化的拐点对应的D0都随µ取值增大而变大。当D0＜2.0 mm 时，µ取不同值对应的DFR 较小，当D0≥2.0 mm 时差异逐渐增大。改变滴谱参数取值时，会得到不同的Ku 波段Z值和C 波段Z值，以1 dBz 为间隔值，对Ku 波段Z值进行分组，每组包含对应的滴谱参数组合，对同一组内对应的滴谱参数组合计算得到的Ku 波段Z值和C 波段Z值分别进行平均，用得到的后者减去前者，得到DFR 随Ku 波段反射率不同产生的变化关系（图6b），图中的拟合曲线即为Ku 波段与C 波段反射率的转换关系。可以看出，当Ku 波段的反射率小于45 dBz 时，不同滴谱参数产生的DFR 差值在0.5 dB 以下，使用滴谱平均得到的转换关系可靠性较高；当Ku 波段的反射率大于45 dBz 时，DFR 对准确的雨滴谱依赖性逐渐增加（这与图6a 中D0＞2.0 mm 的结果对应），选择不同的雨滴谱参数产生的DFR 差异最大将达到2.5 dB。图6c 为通过选择不同的滴谱参数计算得到的Ku 波段和C 波段反射率的对比关系。对于相同的雨滴，Ku 波段的反射率总体大于C 波段，但当Ku 波段反射率大于45 dBz 后差异逐渐变小，但差异的变化幅度逐渐增大，说明对谱参数变化愈加敏感。

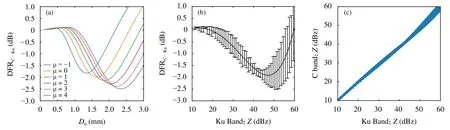
图6 Ku 波段和C 波段在雨区对降水粒子的反射特性（a.µ 取−1—4 时DFR 随 D0取值不同的变化；b.DFR 随Ku 波段降水粒子反射率不同产生的变化，黑色实线代表不同滴谱参数取平均后的结果，误差棒表示标准差；c.Ku 波段和C 波段反射率的散点分布）Fig.6 Comparison of Ku-band and C-band reflection characteristics of precipitation particles in rainy areas（a）The change of DFR with the value of when μ is from 1 to 4；（b）the relationship of DFR with different reflectivity of precipitation particles in Ku-band，the black solid line represents the relationship with average of different drop spectrum parameters，error bars indicate standard deviation；and（c）scatter plot of reflectivity of Ku-band and C-band radar

通过图6b 形成的转换关系，选取2014 年3月—2019 年10 月GPM 卫星雷达在陕西省内的观测样本，将GPM 卫星雷达Ku 波段在不同降水类型中观测到的近地面反射率转换为C 波段对应的反射率，结合由GPM 卫星雷达双波段Ku 和Ka 得出的雨滴谱估计的地面降雨率，得到C 波段雷达定量降水估计的Z-R关系如图7 所示。可见，用Z-R关系进行雷达定量降水估计总体上较为准确，尽管对于中等强度降水估计的准确度会出现一定的下降。由于降水率本质上由雨滴谱决定，这里也隐含着中等强度降水雨滴谱的不确定性更大。

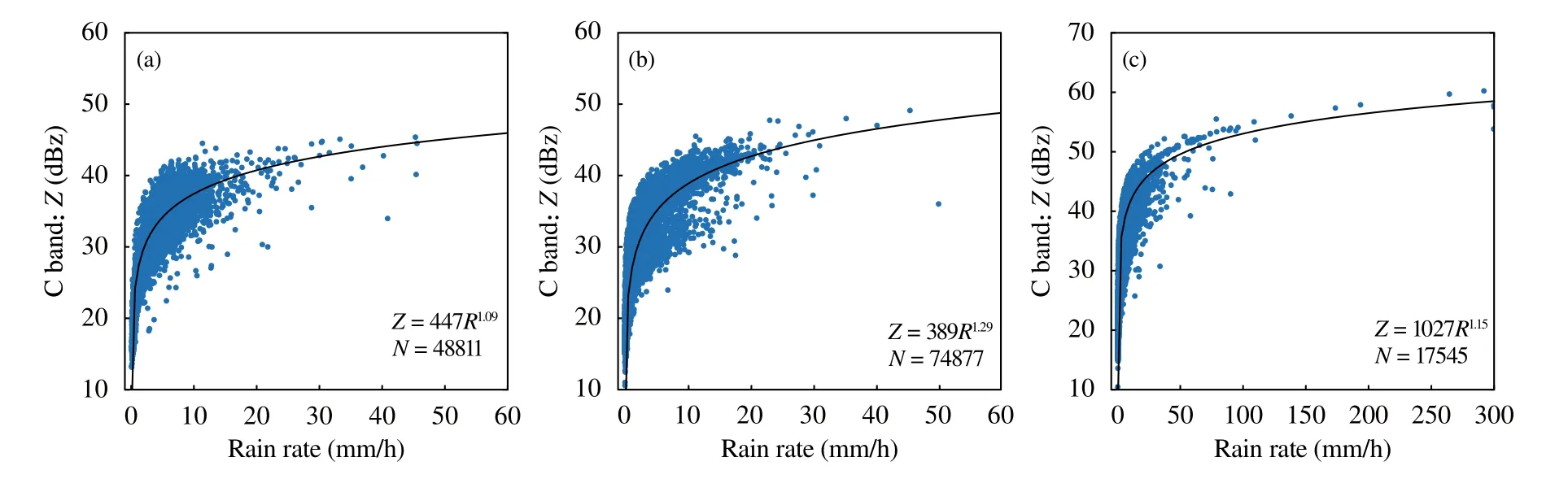
图7 不同降水类型中C 波段雷达降水反演的Z-R 关系（适用于液态降水）（a.0℃层亮带层状云降水，b.非0℃层亮带层状云降水，c.对流性降水；黑色实线为拟合线）Fig.7 The Z-R relationship of C-band radar precipitation for different precipitation types（applicable to liquid precipitation）（a.bright band，b.stratiform，and c.convective；The black solid line is the fitted line）

2.5 基于雷达观测原理的雷达拼图

基于上述模块生成的雷达小时降水率产品和降水类型产品均为单部雷达产品，为便于雷达产品的应用，通常需要将雷达单站产品进行拼图，最终以规则的经纬度网格表示。雷达拼图算法主要是对陕西省7 部雷达的雷达反射率、小时降水率和降水类型分类场进行处理，从而得到空间范围（31.01°—40.00°N，104.00°—113.00°E），空间分辨率为0.01°×0.01°，时间分辨率为6 min 的拼图产品。

对各网格单元而言，拼图需要确定天气雷达网中对其有贡献的雷达及其在雷达平面上对应的位置，即根据网格和雷达站点经纬度计算网格单元在雷达平面上的方位角和径向距离。两点经纬度坐标与两点间距离与方位角的转换关系通常用大圆模型表达（Langston，et al，2007）。

雷达反射率场和小时降水率产品的拼图方法是对各网格单元有贡献的单站雷达反射率和小时降水率进行加权平均，n部雷达各自的权重wi根据式（1）和（3）计算的波束中心高度hc和波束垂直截面直径d确定

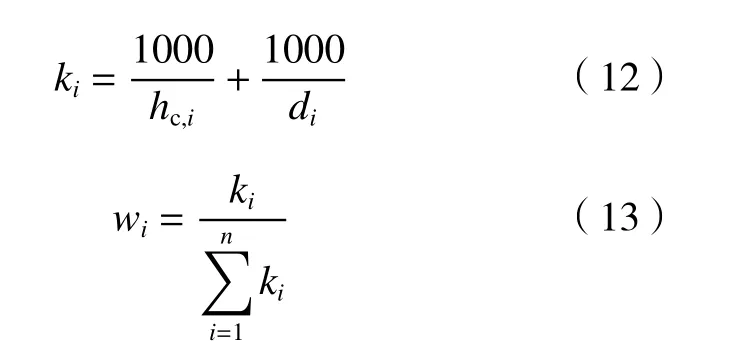
式中，ki为每部雷达对给定网格单元的贡献。对某个网格单元而言，在所有对其有贡献的雷达中，如果波束中心高度最低的雷达没有观测到降水信息，则该网格单元以无效值标识，因为此时较高波束得到的雷达回波很可能来自云砧。而在雷达降水分类产品的拼图算法中，如果某一雷达将网格单元上的降水识别为对流性降水，并且该雷达观测信息离地面较近，则该网格的降水类型标记为对流性降水；如果雷达观测的降水类型为层状云降水，任一网格单元雷达识别出0℃层亮带，则该网格单元的降水类型标记为0℃层亮带层状云降水；如果没有识别出0℃层亮带层状云降水，则标记为非0℃层亮带层状云降水（Qi，et al，2017）。

图8 是2018 年8 月21 日11 时陕西省7 部 天气雷达混合仰角反射率（图8a），降水类型分类场（图8b），1 h 雷达降水率场（图8c）的拼图结果。可以看出，通过赋给雷达不同权重，保证了近距离和低高度的雷达做出更多贡献，保留了反射率场和1 h降水率场的更多细节，使得拼图没有明显的不连续情况，并且能够显示明显的降水强中心，降水类型分类场中对流降水、0℃层亮带降水和非0℃层亮带层状云降水与反射率场、1 h 降水率场基本对应。表明雷达拼图算法能够较好地结合多部雷达，提供较为完整准确的降水信息。

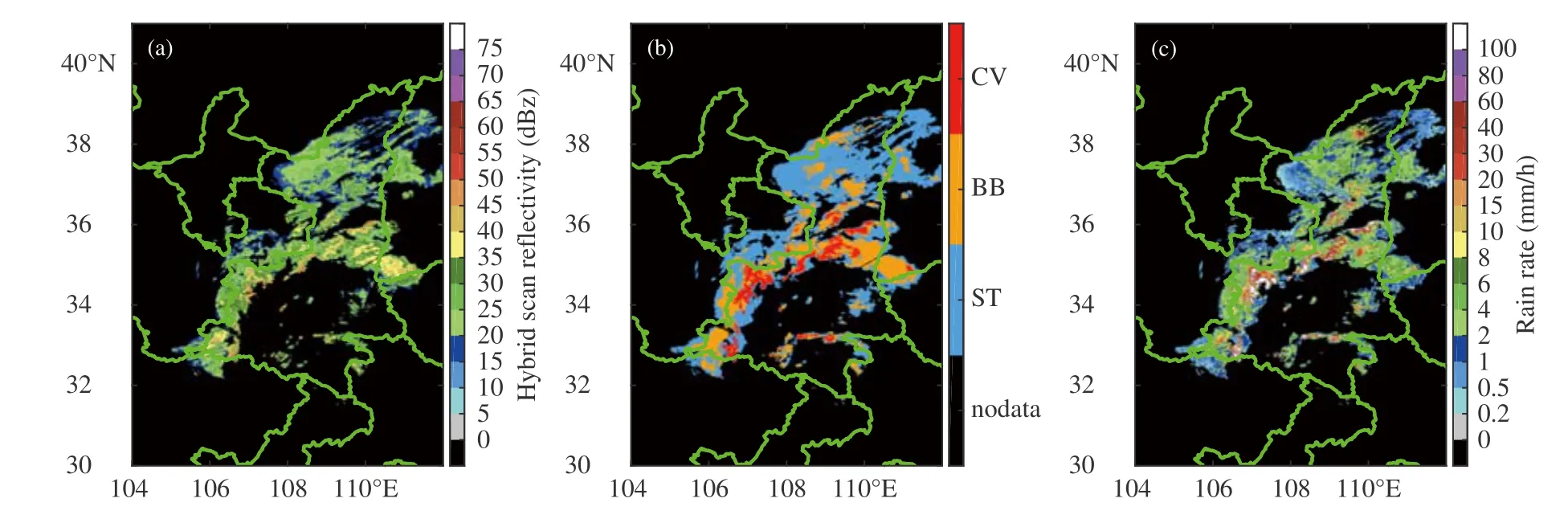
图8 2018 年8 月21 日11 时雷达拼图（a.雷达混合仰角反射率场，b.降水类型分类场，c.1 h 雷达降水率场）Fig.8 Multi-radar mosaic field of（a）reflectivity of hybrid elevation angle，（b）precipitation type，and（c）1 h precipitation rate

3 结果分析

从2019 年5 月26 日14 时—29 日02 时地面雨量站和雷达定量降水估计算法得到的累计降水结果（图9）可以看到，同雨量站累计降水（图9a）相比，定量降水估计算法（图9b）基于最低混合有效仰角对不同的降水类型使用不同Z-R关系进行反演，能够较好地体现降水过程的降水中心、降水范围，对于降水强度的把握比较接近雨量站观测。需要注意的是，陕西雷达仍存在一些非地形遮挡现象，这些遮挡情况无法通过地形数据计算得到，导致部分雷达（如汉中）仍存在部分方位角降水信息不完整的问题。

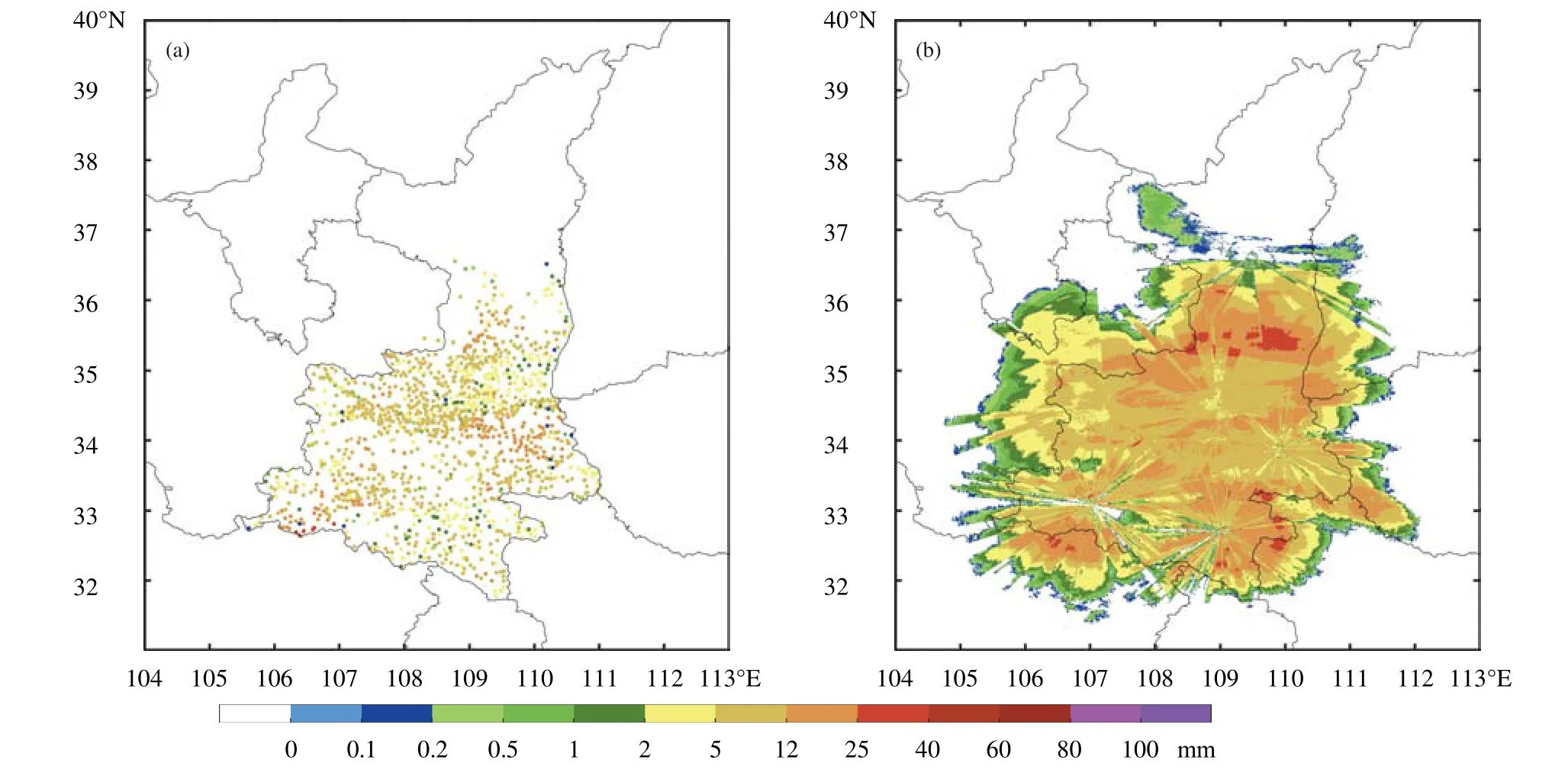
图9 2019 年5 月26 日14 时—29 日02 时累计降水空间分布（a.地面雨量站累计降水观测，b.雷达定量降水估计算法计算得到的累计降水；单位：mm）Fig.9 Accumulated precipitation for the period from 14：00 UTC 26 May to 02：00 UTC 29 May 2019 from（a）surface gauge stations and（b）QPE algorithm described in this paper（unit：mm）

为了更系统地评估文中雷达定量降水估计算法的性能，利用下面3 个统计评分指标进行评估：

（1）均方根误差（RMSE）

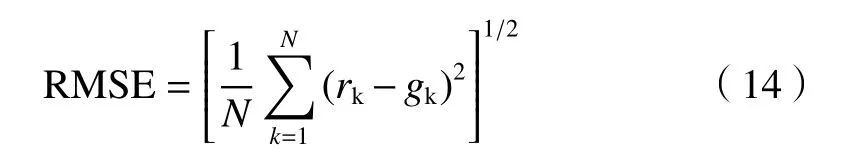
（2）相对误差（RMAE）

（3）相对偏差（RMB）

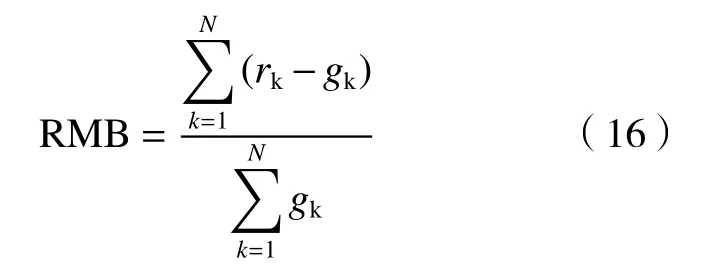
式中，rk和gk分别为雷达估计降水和雨量计观测降水。均方根误差的大小反映了雷达估计降水与雨量计观测降水的离散程度，值越小离散程度越小。相对误差反映了雷达估计降水场的整体精度，值越小精度越高。相对偏差越接近0，说明雷达估计降水与雨量计观测降水越接近。这3 个值越接近0，说明雷达定量降水估计算法性能越好。本研究对定量降水估计产品和雨量计降水数据进行了匹配。根据雨量站的地理位置获取对应的雷达估计降水网格值，与其匹配成为一个数据对，雨量计1 h 降水和雷达估计的1 h 降水分别用g和r表示。对这些数据对进行定量分析，以评估雷达定量降水估计的精度。

图10 为2019 年5 月26 日14 时—29 日02 时累计降水与地面雨量站观测降水散点对比。可以看到，雷达定量降水估计算法基于混合最低有效仰角进行了降水类型分类，并根据降水类型采用相应的Z-R关系，得到的雷达定量估计降水结果其整体趋势基本符合理想曲线，从统计评分指标（RMSE、RMB）也能看出，雷达定量降水估计算法同地面雨量站观测降水较为接近。

图10 2019 年5 月26 日14 时—29 日02 时1 h 累计降水与地面雨量站观测降水散点对比Fig.10 Scatterplots of 1 h precipitation from QPE algorithm described in this paper vs the surface gauge station observations from 14：00 UTC 26 May to 02：00 UTC 29 May 2019

以地面小时雨量站观测为基准，在陕西省选取2019 年4—7 月持续时间较长、影响范围较大的7 次降水过程对文中算法生成的雷达QPE 产品进行评估。表1 给出了这7 次个例的具体信息。图11是这7 次个例两种降水产品的统计评分指标。图11a 中，红点为该次过程中雨量计1 h 平均降水量，蓝点为该次过程中雷达QPE 产品1 h 平均降水量。可以看出，文中算法生成的雷达QPE 产品同地面雨量站观测降水较为接近，特别是过程3 和4，其平均偏差接近于0。总体上，文中算法生成的雷达QPE 产品有一定的低估（RMB 为负值），但基本控制在−30% 以内，过程5 和6 达到−40%（图11c）。这说明该算法生成的雷达QPE 产品在不同过程中的表现比较稳定，这一点从RMAE 指标（RMAE稳定在50%左右，图11b）也可以反映出来。

表1 2019 年陕西7 次降水个例Table 1 The 7 precipitation cases in Shaanxi in 2019

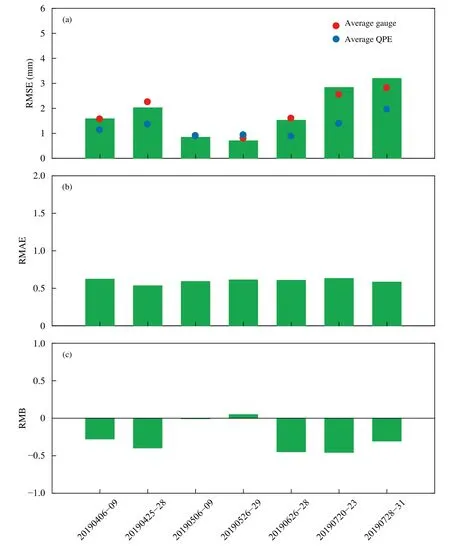
图11 针对陕西7 次降水过程，文中定量降水估计算法结果和地面雨量站降水观测对比统计评分指标（a.均方根误差，b.相对误差，c.相对偏差）Fig.11 Statistical indicators of（a）RMSE，（b）RMAE，and（c）RMB for 7 precipitation processes in Shaanxi

从均方根误差上看，文中算法生成的雷达QPE 产品同地面雨量站观测降水较为接近，7 次过程的均方根误差都在3 mm 以下，过程3 和4 的均方根误差小于1 mm（图11a），雨量计1 h 平均降水量同雷达QPE 产品1 h 平均降水量也比较接近。从相对误差看，雷达QPE 产品较雨量计观测降水误差基本在60%左右。不同过程之间的差异主要是降水平均强度差异导致的。7 次降水过程中，过程6 和7 的降水强度较大，而对应的均方根误差相对较大（3 mm 左右），过程6 的相对偏差也在−30%左右，表明对于中等及以上强度的降水，文中定量降水估计算法估计的准确度会有一定下降，但总体而言，文中算法仍较为稳定，生成的雷达QPE 产品与地面雨量站降水观测相比较为接近。

4 结论与讨论

基于陕西省7 部C 波段天气雷达观测数据，结合雷达探测资料质量控制、降水类型分类、地形遮挡、Z-R关系和雷达拼图等提出了C 波段天气雷达定量降水估测（QPE）算法，生成空间分辨率为0.01°（约1 km），时间分辨率为6 min 的雷达QPE 拼图产品。通过地面小时雨量站的观测数据，对新的雷达QPE 产品进行了评估和比较，主要得到以下结论：

（1）雷达探测资料质量控制算法对地物回波、尖峰等非降水回波和降水回波识别效果较好，能够较好地保留降水信息，但对于降水系统边缘较弱的气象回波有误识别现象，算法需要进一步改进。

（2）通过雷达降水类型分类算法，能够较准确地识别对流性降水、非0℃层亮带层状云降水和0℃层亮带层状云降水。

（3）根据陕西地区雷达遮挡情况，设计了混合最低有效仰角反射率算法，可有效降低地形遮挡导致的降水低估或缺失现象。

（4）利用GPM 卫星雷达反演的滴谱数据对不同类型降水的Z-R关系进行了统计分析，针对不同降水类型采用对应的Z-R关系有利于提高QPE 精度。

（5）文中选取了7 次降水过程，对新算法生成的雷达QPE 产品进行了评估，雷达算法相对稳定，相对误差、相对偏差指标也均表明该算法结果与地面雨量站降水观测结果接近。

与其他地区相比，目前陕西地区雷达QPE 结果和雨量计降水观测之间的偏差依然较大，主要可能有以下几个原因：（1）雨量计质量问题；（2）雷达受地形阻挡探测不到；（3）雷达电磁波部分受地形遮挡导致能量削弱；（4）陕西雷达存在一定的非地形遮挡现象；（5）部分地区可能存在地形对降水的增强，导致在近地面降水具有较大增幅，尤其是强的对流性降水，使得雷达QPE 偏低。另外，虽然C 波段电磁波衰减远小于Ku 波段，但C 波段天气雷达的水平观测距离为近百千米，而GPM 星载双频雷达（DPR）Ku 波段在垂直方向只有几千米雨区，因此C 波段天气雷达的衰减可能远大于DPR Ku 波段的衰减，从而导致雷达QPE 偏低，尤其是有较大范围强降水和强冰雹时，C 波段雷达衰减问题会更加严重。同时，由于DPR 数据本身也存在误差，例如由于地物杂波、非均匀充塞导致的Z值观测误差，虽然在算法中对这些误差进行了订正，但不能完全消除；此外，根据滴谱参数反演的R值也存在一定误差。由于陕西地形复杂，雷达电磁波遮挡问题较为严重，因此，仅依靠雷达观测数据，在地形遮挡严重的区域难以获取较为准确的降水量信息。未来应结合卫星数据和质量控制后的地面雨量站数据对雷达受遮挡范围进行补充，进一步提高QPE 精度。

目前，中国正在进行双偏振雷达的升级工作，在未来几年中，陕西省雷达也会逐渐升级为双偏振雷达，双偏振雷达提供的多个偏振量能够反映降水的滴谱信息，从而更好地描述降水特征，引入偏振量信息，将促进定量降水估计精度的提高。