用函数观点处理递推数列的模式
◎贾广素 齐 伟 (山东省孔子国际学校,山东 济宁 272000)
一、利用函数的图像研究数列的性质
若将数列{an}的递推式记成an+1=f(an),a1=f(x),则a2=f(a1)=f(f(x)),a3=f(a2)=f(f(f(x))),…,此过程可如此继续下去,数列的递推问题实质就是函数的迭代问题,可以用“蛛网模型”作图展示,直观分析出函数的单调性、有界性、周期性等.

A.2019 B.2018 C.4038 D.4037
(2019年清华大学THUSSAT测试)
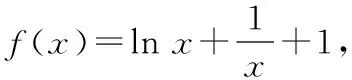

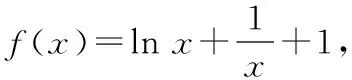

(2019年杭州市二模拟)
解析考虑函数f(x)=-x2+cx-1,在同一坐标系中作出f(x)=-x2+cx-1与y=x的图像.
如果c≤0,则a2≤0,不满足{an}单调递增,从而知c>0.由a2=-1+c-1>a1=1,知c>3.

如果AB段不是单调递增的话,就会出现如图所示左右摆动转圈圈的情况,这显然不满足{an}单调递增.
二、利用不动点理论简化递推关系
当已知数列的首项a1和递推式an+1=f(an)时,可以提炼an+1与an的函数关系式y=f(x),若方程f(x)=x有根x0(此根为函数y=f(x)图像与函数y=x图像交点的横坐标),就可以将递推式变成以下两种情形:
情形一an+1-x0=f(an-x0),令bn=an-x0,代入消元得bn,将问题转化为研究数列{bn};
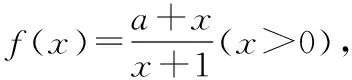
(2020年山东省模拟考试)

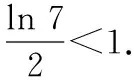


从而原不等式得证.
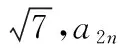

C.当b=-2时,a10>10 D.当b=-4时,a10>10
(2019年浙江省高考)

对于选项C:令an+1=an=x,x=x2-2,即x2-x-2=0,由(x-2)(x+1)=0,则x=-1或x=2,令a=-1,则a10=-1<10,故C错误;

三、利用函数的值域研究数列的范围
对于已知数列首项a1和递推式an+1=f(an),求证:G(an) (2020年济南市一模) 如果所证式一侧为某个数列的前n项和的形式,我们也可将待证不等式的另一侧看作是另一个数列的前n项和,通过研究相对应项之间的大小关系,从而使不等式的证明得以解决. (1)判断x>0时,f(x)-h(x)的零点个数,并加以说明; (2)正项数列{an}满足a1=1,ane-an+1=f(an). ①判断数列{an}的单调性,并加以证明; (2020年山东省三校联考) 令φ(x)=ex-x-1,x>0,从而φ′(x)=ex-1>0,所以φ(x)在(0,+∞)上单调递增,又φ(x)>φ(0)=0,所以f(x)-h(x)>0,从而f(x)-h(x)的零点个数为0. (2)由于ane-an+1=f(an),知an+1=lnan-lnf(an),从而可知 an+1-an=lnan-lnf(an)-an=lnan-[ln(ean-1)-an]-an=lnan-ln(ean-1) 由(1)知,当an>0时,有1+an 从而an+1 令g(x)=2xex-e2x+1(x>0),从而g′(x)=2ex+2xex-2e2x=2ex(1+x-ex),由(1)知1+x-ex<0,从而g′(x)<0,g(x) 递推数列作为高考数学的一块十分重要的内容,如何用函数的方法统一高效地帮助学生思考此类问题是高中教师备考的重点,希望本文能给大家提供一些帮助.


四、将数列前n项和问题转化为项的范围


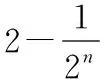
结束语

