基于度中心性的认知特征选择方法

张笑非，杨 阳，黄佳进，钟 宁，5*

（1.北京工业大学信息学部，北京 100124；2.江苏科技大学计算机学院，江苏镇江 212003；3.磁共振成像脑信息学北京市重点实验室，北京 100124；4.北京林业大学人文社会科学学院，北京 100089；5.前桥工科大学生命科学与信息学系，群马前桥371-0816，日本）

（*通信作者电子邮箱zhong@maebashi-it.ac.jp）

0 引言

人脑包含诸多功能特定的脑功能网络（Functional Brain Network，FBN），每个功能网络又由特定的兴趣点（Region Of Interest，ROI）构成。人脑在执行需要注意力的认知任务时，一些脑区的活跃度会增加，而另一些则会降低。功能核磁共振成像（functional Magnetic Resonance Imaging，fMRI）研究的一个热点就是对大脑血氧水平依赖（Blood Oxygen Level Dependent，BOLD）活动所蕴涵的信息进行分析。Naselaris等［1］认为fMRI 编码/解码（Encoding/Decoding）是两个互补的操作，其中fMRI 解码能够通过BOLD 活动来预测实验刺激相关信息。Correia 等［2］通过对双语被试口语单词翻译的fMRI解码研究，发现口语翻译过程中语义信息的激活再现发生在大脑前颞叶中。故大脑皮质体素或大脑图谱ROI选择的合理性对于fMRI解码的有效性至关重要。因此，本文提出一种在fMRI功能连接ROI度中心性（Degree Centrality，DC）计算的基础上，通过统计对比入组被试整体相同ROI 在执行认知任务时不同认知状态间的差异显著性，并以此差异显著性作为认知特征选择的依据。此外，在认知特征选择结果的基础上，计算人脑认知体系子系统的认知特征指数（Cognitive Feature Index，CFI）和相应的人脑认知系统曲线下面积（Human Brain Cognitive Architecture-Area Under Curve，HBCA-AUC），从而对提出的方法和其他特征选择方法进行比较。

1 人脑认知体系与认知特征

Fox 等［3］通过研究人脑静息状态下对是否任务相关的二分表现程度，发现了大脑在执行目标导向任务时活跃加强脑区所构成的任务正相关网络（Task Positive Network，TPN），以及活跃降低脑区所构成的任务负相关网络（Task Negative Network，TNN）；此外，初级感觉与运动皮质由于对这两类网络都没有内在的偏好，因此不属于这两类网络中的任意一个。如图1（a）所示，Power 等［4］通过静息态功能核磁共振成像（resting state fMRI，rs-fMRI）功能连接研究了健康成年被试的脑功能结构，发现了任务正相关系统（Task Positive System，TPS）由至少3 个主要的子网络构成，即背侧注意网络（Dorsal Attention Network，DAN）、前额叶-顶叶网络（Frontal-Parietal Network，FPN）、扣带回-岛盖网络（Cingulo-Opercular Network，CON），而任务负相关系统（Task Negative System，TNS）仅仅由一个子网络构成，即默认网络（Default Mode Network，DMN）。Yeo 等［5］研究认为，TPN 包括FPN、DAN，以及腹侧注意网络（Ventral Attention Network，VAN）。Hermans等［6］的研究认为显著网络（Salience Network，SN）也属于TPN。Carhart-Harris 等［7］和Tagliazucchi 等［8］以及将视觉网络、听觉网络、体动网络归类为低阶认知网络（Lower Cognitive Network），区别于TPN 和TNN 共同构成的高阶认知网络（Higher Cognitive Network）。Markwalter 等［9］认为小脑整合传递有关内部和外部环境信息的各种神经输入，虽然小脑输入的功能和组织对运动协调、适应和学习等认知活动的作用还有很多未解之谜，但是其毋庸置疑是人脑感觉运动处理的关键中心。因此，本文将视觉网络（Visual Network，VN）、听觉网络（Auditory Network，AN）、感觉-运动网络（Sensori-Motor Network，SMN）、小脑网络（Cerebellum Network，CN）都归类为任务支撑系统（Task Support System，TSS）。综上，本文将人脑认知体系定义为三大系统，即TPS、TNS、TSS。由于Power-264中的记忆提取网络（Memory Retrieval Network，MRN）、皮质下网络（SubCortical Network，SCN）缺少文献证据，以及还拥有一个包含28个ROI功能网络非确定的集合，因此对Power-264的人脑认知体系划分结果如图1（b）所示。

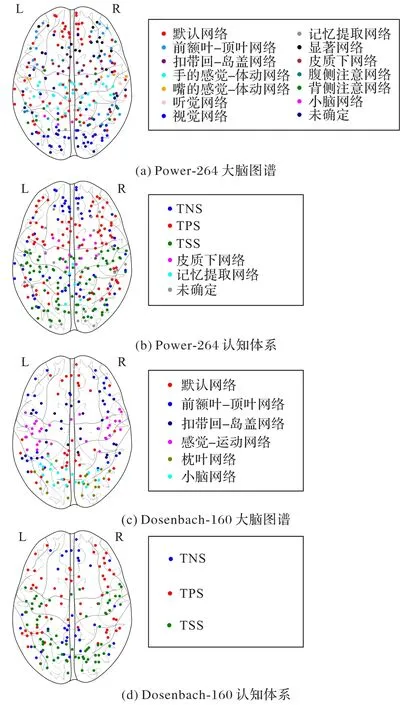
图1 大脑图谱的功能网络及其认知体系Fig.1 Functional networks of brain atlases and their cognitive architectures

图1（c）给出的是大脑图谱Dosenbach-160［10］中定义的160个ROI和对应的6个脑功能网络，图1（d）是将其160个ROI在人脑认知体系上的划分结果。如表1 所示，其每个脑功能网络都能明确对应到TPS、TNS、TSS 中的一个，即每个ROI 能够划分到人脑认知体系的特定子系统，此时将ROI 作为认知特征则具有较好的解释性。不同于以解剖学定义大脑谱图AAL（Automated Anatomical Labeling）［11］进行的fMRI 研究、如宋源等［12］通过统计特性随机森林进行特征选择从而更好地识别出精神分裂症患者，对人脑认知活动的研究依赖对人脑认知体系的深入理解。当然，对包括Dosenbach-160、Power-264 等大脑图谱在人脑认知体系上划分的准确性并不是本文的研究重点，而是旨在对特定认知任务下产生的fMRI数据进行有效的认知特征选择，并能够利用人脑认知体系子系统自身功能的特异性对认知特征选择的准确性进行评价。

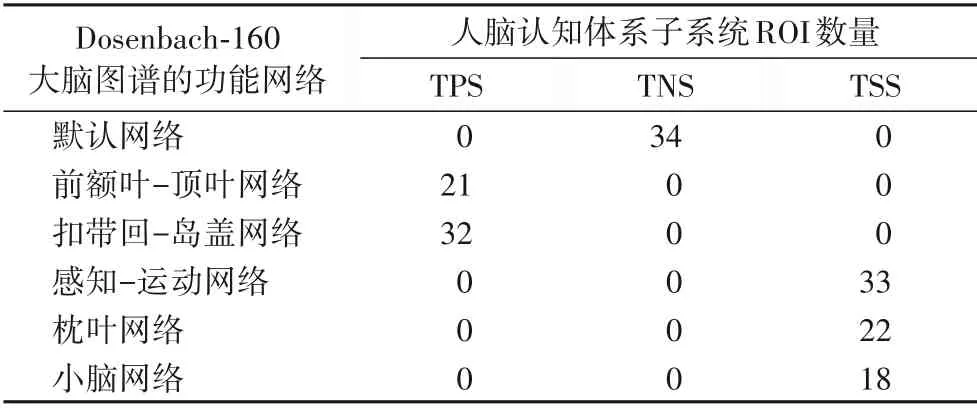
表1 Dosenbach-160大脑图谱的人脑认知体系划分Tab.1 Human brain cognitive architecture division of Dosenbach-160 brain atlas

2 方法框架及评价标准

2.1 认知特征选择方法

度中心性是研究大脑网络的一种基本指标，例如，夏锐等［13］通过研究遗忘型轻度认知障碍患者静息态fMRI脑网络、认为度中心性是一种衡量情景记忆能力的潜在指标。因此，本文提出一种基于度中心性的脑功能网络特征选择方法（Degree Centrality based Cognitive Feature Selection Method，DC-CFSM），其框架包括两个阶段，如图2 所示。其中第一阶段（Stage1）是对认知实验产生的fMRI 数据进行功能连接分析，得到每个ROI在不同实验条件下的度中心性，即大脑图谱中与该ROI共激活（co-activation）的ROI数量占比。第二阶段（Stage2）则对相同ROI 在执行认知任务时不同认知状态的度中心性进行统计对比，根据差异的显著性进行认知特征的选择，即差异越显著则越适合作为认知特征。

图2 DC-CFSM的框架Fig.2 Framework of DC-CFSM

2.1.1 ROI度中心性

度中心性的计算首先需要构建大脑图谱的功能连接矩阵，即计算每对ROI 之间的关联系数，通常采用Pearson 关联系数r值。r值本身是一个［-1，+1］内的浮点数，在判断相应ROI对之间是否存在网络概念上的边时，本文则在其r值基础上求得认知实验入组被试s在认知状态c下的关联显著性矩阵Ps，c，如式（1）所示：

其中：ps，c，i，j是被试s在认知状态c下大脑图谱第i个ROI 和第j个ROI 之间的关联显著性P值；n是大脑图谱中ROI 的个数。由于ps，c，i，j=ps，c，j，i，即Ps，c是一个对称矩阵。此外，因为每个ROI 自身是完全相关，因此ps，c，i，i为0，即Ps，c对角线上的元素都为0。

其次，通过关联显著性ps，c，i，j值判断相应ROI 对之间是否存在网络概念上的边时，需要通过显著性水平（Significance Level）α值作为阈值进行判断，即ps，c，i，j<α时，则认为ROI 对之间存在网络概念上的边；反之则不存在。因此，该值的选择对之后的度中心性计算结果将产生重要的影响，但更需要重视的一个问题就是统计分析上是否存在假阳性，这里采用FDR（False Discovery Rate）方法进行校正，Ps，c经过校正后得到P's，c，如式（2）所示：

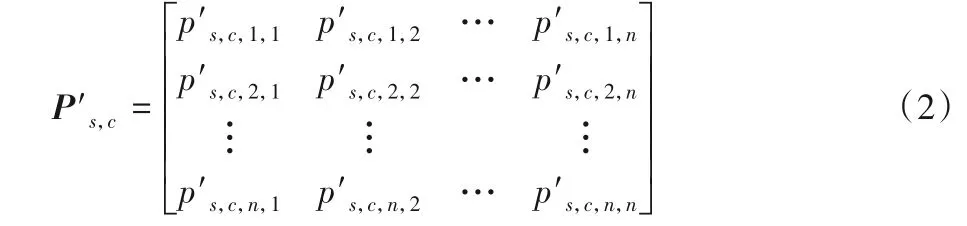
其中：p's，c，i，j是ps，c，i，j经过校正后被试s在认知状态c下大脑图谱第i个ROI和第j个ROI之间的关联显著性P值；P's，c仍然是一个对角线元素均为0的对称矩阵。这里，α值设为统计分析常用的0.05，则可由P's，c得到邻接矩阵As，c，如式（3）所示：

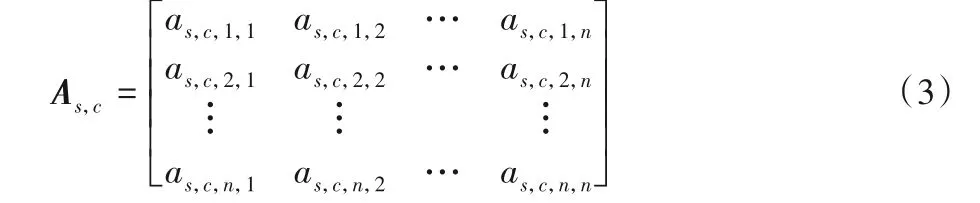
其中：As，c是一个对角元素全为0 的对称二值矩阵。对于As，c中的非对角线元素as，c，i，j，当P's，c中相应元素p's，c，i，j<α且i≠j时，as，c，i，j=1；反之as，c，i，j=0。

最后，被试s在认知状态c下大脑图谱第i个ROI 的度中心性DCs，c，i的定义如式（4）所示：

2.1.2 认知特征显著性

认知特征显著性本质上就是量化被试组所有被试同一ROI 的某个属性对于认知任务不同认知状态的区分度，通常对认知状态区分度越大的ROI越适合作为认知特征。为了方便统计对比不同认知状态同一（如第i个）ROI的度中心性，首先将所有入组的所有被试在同一认知状态c下同一（如第i个）ROI度中心性构成一个序列DCc，i，如式（5）所示：

其中S是认知实验中所有入组被试构成的被试集合。

每一个（如第i个）ROI对认知状态的区分能力，即认知特征显著度CFSi定义如式（6）所示：

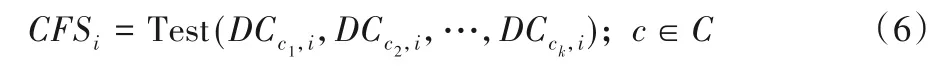
其中：C是认知实验中所有实验条件诱发的认知状态所构成的认知状态集合；|C|表示C中元素的数量，k=|C|且|C|≥2；Test 是所选择的统计检验方法，对输入的多个度中心性序列DCc，i(c∈C)进行统计对比并返回差异显著性P值。当k=2时，Test可以采用T 检验、卡方检验；当k≥3时，Test可以采用方差分析（ANalysis Of VAriance，ANOVA）。大脑图谱中ROI的认知特征显著度数值越小，越适合作为认知特征。

2.2 认知特征评价方法

本文对认知特征评价的基本思路是对人脑认知体系每个子系统所包含ROI 的认知特征显著性相对大脑图谱所有ROI的认知特征显著性在序上的优先性进行度量。因此，这里设计了一个用于评价人脑认知体系的CFI 计算算法，其中BA是大脑图谱中所有ROI 构成集合，CFS是大脑图谱所有ROI 的认知特征显著度CFSi所构成的集合，BA中的元素与CFS中的元素一一对应。HBCA（人脑认知体系）是一个集合的集合，其自身元素TXS（认知子系统）是一个由大脑图谱BA中ROI 构成的非空集合，BA中每个ROI 属于且仅属于HBCA的一个元素，即TXSu∩TXSv=∅，u≠v，且TXSu=BA。算法返回参数CFIS（认知特征指数集）是一个集合，其每一个元素CFIu（认知特征指数序列）是与HBCA每一个元素TXS（u认知子系统）相对应的单调递增序列，|CFIu|=|BA|+1 且|CFIu|=|CFIv|(u≠v)。算法的具体步骤如下：

CFIS的元素CFI是一个从0到1的单调递增序列，该序列对应曲线的线下面积代表HBCA中相应认知子系统所包含ROI 作为认知特征的整体质量，即线下面积越大表示该认知子系统在认知实验过程中的作用越大。因此，认知子系统的认知特征指数CFI对应的人脑认知体系线下面积如式（7）所示：

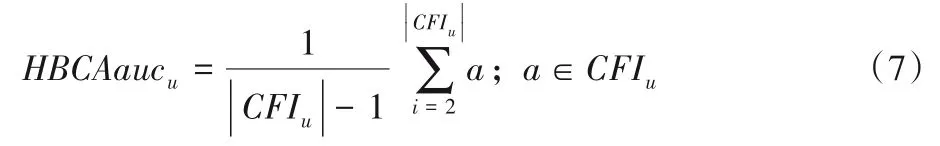
其中：CFIu是HBCA中第u个认知子系统对应的认知特征指数序列。CFIu中的第一个元素0只是为了便于CFI算法设计，并不参与HBCAaucu值的计算。

3 实验与结果分析

实验数据来自国际网络智能协会（Web Intelligence Consortium，WIC）研究院（http：//wi-consortium.org/）的认知实验“简单加法/减法心算”［14-15］，该认知实验目标是研究人脑在进行简单加法或简单减法时大脑神经活动的规律，共接受了21 名（男12，女9）统计学上无差异的受试者参加。该实验由WIC 团队在首都医科大学宣武医院进行、并获得院方伦理委员会的批准。

fMRI 数据处理包括预处理和基于DC-CFSM 的认知特征选择两个阶段。第一阶段的预处理是采用SPM（Statistical Parameter Mapping）［16］完成，包括切片时间校正、头动校正、空间归一化，以及平滑处理四个步骤。第二阶段认知特征选择DC-CFSM 的实现采用的是Python 语言及相应的工具包，其中神经影像处理基本操作采用的是NiBabel（https：//nipy.org/nibabel/），Pearson 关联系数计算、FDR 校正，以及统计检验对比采用的是SciPy［17］。

本文利用提出的DC-CFSM 计算出Dosenbach-160 大脑图谱每个ROI分别在简单加法认知状态和简单减法认知状态下的度中心性，然后通过在被试群体上对每个ROI 在两种心算认知状态下的度中心性进行T检验统计对比，并根据T检验P值的显著性作为认知特征选择的依据。图3 给出了差异性P值小于0.05共25个ROI在两种认知状态下的度中心性值，这些ROI来自TPS、TNS及TSS的数量分别为18、0和7。

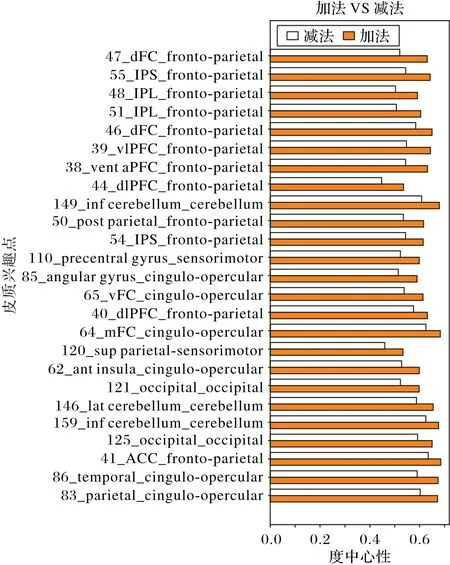
图3 基于DC-CFSM的认知特征排序结果Fig.3 Ranking results of cognitive features based on DC-CFSM

图4 给出的是基于Dosenbach-160 的CFI 曲线和HBCAAUC 结果，TPS、TNS 及TSS 的HBCA-AUC 值分别为0.669 2、0.304 0 和0.468 5。TSS 中最优认知特征是Dosenbach-160 中的18 号ROI，该ROI 是前扣带回皮质中的一个区域，在所有ROI 中也只能排到第38 位，即TSS 的CFI 曲线首次上升的横坐标位置。TPS 中的ROI 占据了Dosenbac-160 中最优的8 个认知特征，且全部来自TPS 中的前额叶-顶叶网络，这与Artemenko等［18］认为成人大脑的心算加工依赖于前额叶-顶叶网络的观点相符合。因此，其CFI曲线在横坐标最开始的8个坐标点上一直处于上升过程，其HBCA-AUC 相较于TNS 和TSS 更高、CFI 曲线也最先达到了最高值。TPS 中最劣认知特征是Dosenbach-160 中的74 号ROI，即中脑岛的一个区域，在其之后还有7个ROI和5个ROI分别来自TNS和TSS。

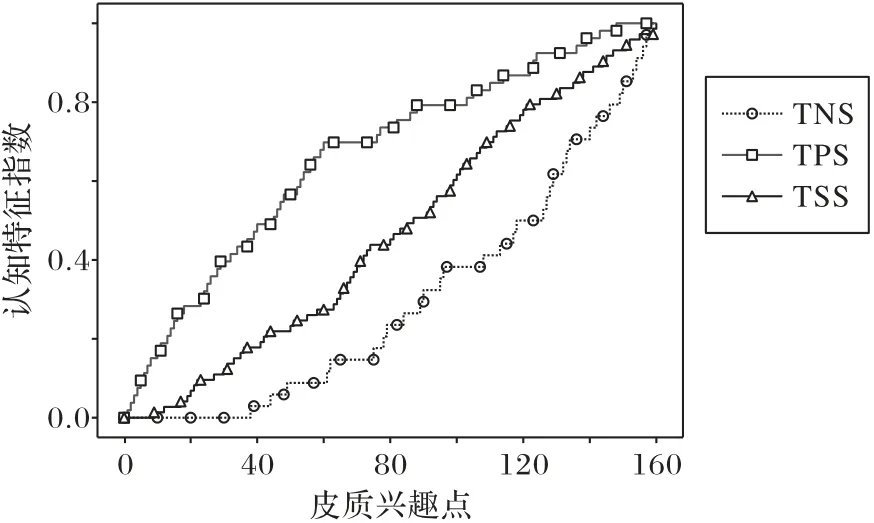
图4 DC-CFSM的HBCA-AUC Fig.4 HBCA-AUC of DC-CFSM

实验在相同fMRI 数据上使用了极限树（Extremely randomized Trees，Extra Trees）、自适应提升（Adaptive Boosting，AdaBoost）、随机森林（Random Forest）、极限梯度提升（eXtreme Gradient Boosting，XGB）这4种方法计算了Dosenbach-160 中所有ROI 的特征值并进行了排序，并在此基础上计算了人脑认知体系三个子系统的HBCA-AUC 值，其结果与DC-CFSM 的结果如图5 所示。Extra Trees、AdaBoost、随机森林、XGB、DC-CFSM 这5 种方法在TPS 上的HBCA-AUC 分别为0.547 8、0.587 5、0.538 3、0.487 8 和0.669 2，这说明DCCFSM 在这5 种方法中最倾向于选择TPS 中的ROI 作为认知特征。同样，这5 种方法在TNS 上的HBCA-AUC 分别为0.382 2、0.432 3、0.552 2、0.456 3 和0.304 0，这 说 明DCCFSM 在这5 种方法中最不倾向于选择TNS 中的ROI 作为认知特征。

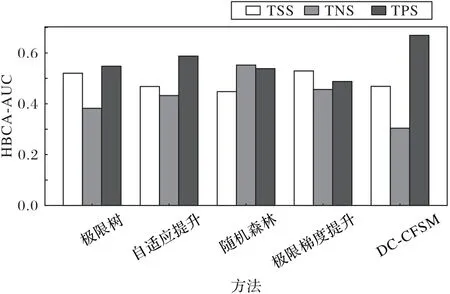
图5 不同方法的HBCA-AUC值Fig.5 HBCA-AUC values of different methods

如表2所示，采用DC-CFSM 时TPS 的HBCA-AUC 值（0.669 2）比极限树、自适应提升、随机森林、极限梯度提升这4 种方法的HBCA-AUC 值，即识别率分别提高了22.17%、13.90%、24.32%和37.19%。相应地，采用DC-CFSM 时TNS的HBCA-AUC 值（0.304 0）比其他4 种方法的HBCA-AUC 值，即误识率分别降低了20.46%、29.70%、44.96%和33.39%。

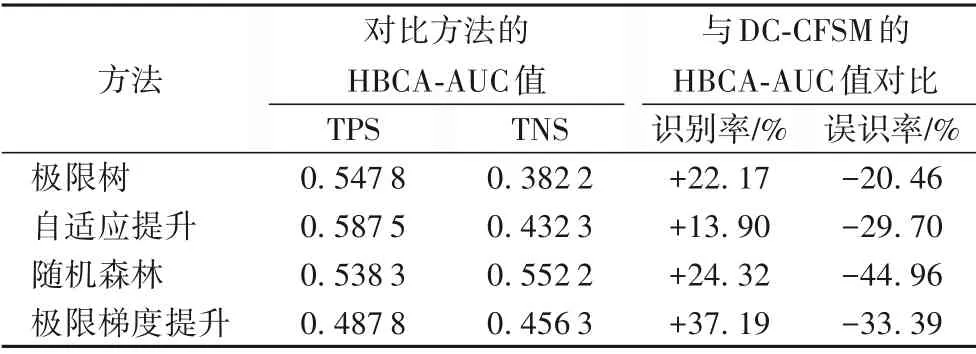
表2 DC-CFSM与其他方法的性能对比Tab.2 Performance comparison between DC-CFSM and other methods

Arsalidou等［19］对数字和心算涉及的大脑区域进行的元分析（Meta-Analysis），Dehaene 等［20］对大脑心算进行的通路分析，Klein 等［21-22］利用概率纤维跟踪方法得到心算处理通路的证据及对数字认知中三码模型结构连接的分析，都表明心算处理始终会激活成人大脑TPS 中的FPN，包括顶上小叶（Superior Parietal Lobule，SPL）和顶下小叶（Inferior Parietal Lobule，IPL）等顶叶区域，以及额叶下回（Inferior Frontal Gyrus，IFG）、额中叶等额叶区域回（Middle Frontal Gyrus，MFG）和左上额回。Peters 等［23］通过回顾分析，认为儿童的心算处理通常也会涉及到一个与成人心算类似的FPN。Wallis等［24］认为FPN 和CON 在控制工作记忆中起不可分割的作用，其中FPN在注意准备和记忆定向期间负责感知皮层自上而下的活动调节，而CON 在认知控制中起到偏下游的作用、可能与记忆的输出门控有关。Hagiwara 等［25］对心算任务中的工作记忆进行了功能连接分析，发现额叶和顶叶在工作记忆任务中会协同工作。Dimitriadis 等［26］通过研究发现DMN（TNS 中唯一的功能网络）在执行心算任务时可能会出现钝化，并认为该钝化现象可能源于认知任务期间功能网络活化的抑制作用。

虽然Extra Trees 的结果从心算认知机制上具有可解释性，但其计算得到HBCA-AUC 在TPS 上的结果并不显著高于在TSS 上的结果。类似地，AdaBoost 计算得到HBCA-AUC 在TSS 上的结果也不显著高于在TNS 上的结果。随机森林方法得到的HBCA-AUC 在TNS 上的结果比TPS 上的结果略高，这使得在心算认知机制上很难解释。XGB 方法得到的HBCAAUC 在TPS 上的结果虽然比在TNS 上的结果略高，但均低于在TSS 上的结果，这使得对心算认知机制解释时具有一定的难度。DC-CFSM 得到的HBCA-AUC 在TPS 上的结果均显著高于在TNS 和TSS 上的结果、且在TSS 上的结果也显著高于在TNS 上的结果，因此，相较于其他4 种方法，DC-CFSM 在认知特征选择上具有最好的心算机制解释性。

4 结语

本文基于脑功能网络的度中心性度量，以ROI 在不同认知状态下的差异显著性作为认知特征选择的依据，通过HBCA-AUC 对几种方法的性能进行了对比，验证了本文提出的DC-CFSM在认知特征选择上的优越性。具体体现为：

1）基于人脑功能划分定义人脑认知体系及其子系统，并对所参考大脑图谱的ROI 进行归属划分，使得认知特征的选择和排序具有更好的解释性；

2）常规的特征选择方法只是从计算方法上进行特征的选择，而以度中心性作为特征选择的依据更能突出ROI 之间共激活而表现出的全局性；

3）本文方法得到的认知特征排序结果更加偏向TPS、且更加偏离TNS，相较于其他方法的结果在认知神经科学上具有更好的自洽性。

虽然本文方法得到的结果在性能评估上最优、且具有更加合理的认知神经科学解释性，但作为特征能够对认知计算模型的作用还有待进一步研究。此外，本文方法的通用性还需要在多样性的大脑图谱和多来源的fMRI 数据集上作进一步验证。