带螺旋内筋薄壁筒形件旋压变形特征
吕 伟 詹 梅 王 鹏 马 飞 高鹏飞
(1 西北工业大学材料学院,西安 710072)
(2 北京宇航系统工程研究所,北京 100076)
(3 四川航天长征装备制造有限公司,成都 610100)
0 引言
带螺旋内筋薄壁筒形件是一种在航空航天领域广泛应用的关键承力构件,其内部设计有交错分布的螺旋加强筋,能大幅提高该类构件的强度和刚度。随着我国航空航天等领域高端装备的迅速发展,特别是新一代运载火箭的研制,对此类构件的整体化、高性能和轻量化提出了更高的要求。旋压作为一种局部增量塑性成形技术,被广泛应用于制造高精度薄壁筒形件[1],其通过旋轮的局部连续加载使工件产生塑性变形,具有成形载荷低、工件性能好、可以实现大型构件整体成形等优点[2],是实现带螺旋内筋薄壁筒形件高性能整体成形制造的优势技术。
由于旋压技术在成形带内筋构件上的独特优势,国内外学者在带内筋构件旋压成形理论及工艺研究方面做了大量探索性的工作,其中构件的内筋形式主要以横筋和纵筋为主。MA 等[3]研究了带横向内筋构件旋压塑性变形行为,获得了内筋充填过程中3种典型的塑性变形行为特征:不饱满内筋塑性变形行为、饱满内筋塑性变形行为和不稳定塑性变形行为。其中在最理想的饱满内筋塑性变形行为中,旋轮作用下内筋处内层材料径向受压应力,切向和轴向受拉应力。古创国[4]分析了带横向内筋构件旋压成形过程中筋部的金属流动、应力应变分布规律,揭示了带横向内筋构件筋部成形机理。在带纵向内筋构件旋压成形研究中,JIANG 等[5−6]通过有限元模拟获得了带纵筋筒形件旋压成形过程中不同区域的应变特征,发现工件不同区域的应变特征存在明显差异,筒壁区材料的应变模式为径向压缩应变,切向和轴向为拉伸应变,而纵筋的应变模式为径向和轴向拉伸应变,切向为压缩应变。HAGHSHENAS等[7−8]通过显微硬度表征的方法获得了带纵筋筒形件旋压成形不同区域的塑性应变分布特征,并对比分析了不同铝合金材料旋压后性能差异,为带纵向内筋筒形件旋压成形变形特征的实验表征及旋压材料的选取提供了借鉴。ZENG 等[9]通过有限元模拟获得了带纵横交叉内筋薄壁筒形件旋压变形特征,发现筒壁区材料在旋轮作用下处于三向压应力状态,而内筋处由于筋槽的存在,其内层材料径向受压应力,切向和轴向受拉应力。同时,纵筋和横筋的应变类型也存在差异,纵筋的径向压缩应变和较大的轴向拉伸应变使得其充填高度低于横筋,而横筋的外层材料径向为压缩应变,内层材料为径向拉伸应变。在带螺旋内筋筒形件旋压成形研究方面,GROCHE 等[10]研究了带单一旋向螺旋内筋筒形件旋压成形工艺,其研究重点在成形方法上,并未涉及充填过程中的变形特征。冯苏乐等[11]通过实验研究了带螺旋交叉内筋筒形件固溶态温旋成形工艺,设计了该类构件的固溶−温旋−人工时效加工工艺路线,为此类构件的工程应用提供了指导。以上对带内筋构件旋压变形特征的研究主要集中在横筋和纵筋上,缺乏对带螺旋内筋薄壁筒形件旋压变形特征的研究,阻碍了此类构件旋压变形行为的主动调控和旋压技术的发展。
本文采用有限元仿真软件建立带螺旋内筋薄壁筒形件有限元模型,在此基础上对旋轮作用下不同区域的应力特征及成形工件不同区域的应变特征进行分析,据此获得带螺旋内筋薄壁筒形件旋压变形特征,拟为此类构件旋压变形行为主动调控提供指导。
1 实验
1.1 有限元建模
基于作者先前建立的带螺旋内筋薄壁筒形件旋压成形有限元模拟开展研究[12]。模型采用ABAQUS/Explicit仿真平台建立,几何模型主要包括旋轮、筒坯和带螺旋筋槽的芯模。其中芯模的结构比较复杂,如图1所示,芯模直径为200 mm,其外表面分布有螺旋角β=45°的右旋筋槽和螺旋角为−β的左旋筋槽。螺旋筋槽的具体结构如图所示,其中螺旋筋槽的外宽w0=7.93 mm,深度h=5 mm,筋槽圆角半径r=3 mm,筋槽侧壁夹角α=16.32°。旋压筒坯采用6061铝合金,其内径为200.5 mm,壁厚为7.75 mm。旋轮采用筒形件旋压常用的双锥面旋轮,旋轮直径300 mm,成形角22.5°,圆角半径10 mm。
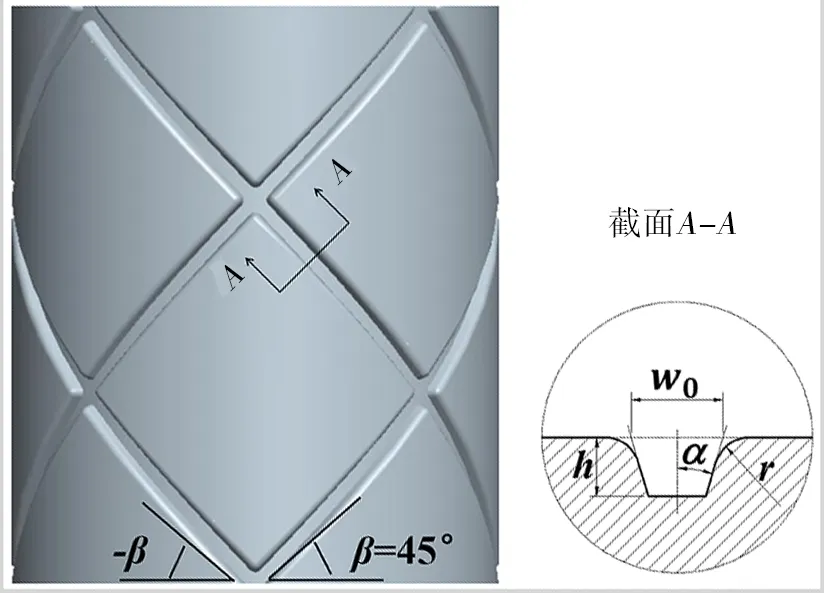
图1 芯模螺旋筋槽尺寸图Fig.1 Dimensions of spiral groove on mandrel
通过拉伸实验获得6061铝合金材料的真实应力−应变数据,并采用各向同性硬化模型描述其应力−应变关系:σ=216.2(0.0044 +ε)0.21MPa,相应的材料力学性能参数为:屈服强度σ0.2=69.2 MPa、弹性模量E=69.3 GPa、泊松比v=0.3、密度ρ=2 700 kg/m3。
在有限元建模过程中,旋轮和芯模定义为刚体。筒坯定义为变形体并采用C3D8R 单元对其离散化,其中沿厚度方向划分5层,切向和轴向的单元数量分别为600 和200。为了保证有限元计算过程中单元不会因大变形出现畸变,对变形区单元采用了ALE网格自适应技术。建模过程中,将芯模固定,筒坯的底面与芯模耦合,采用幅值曲线定义两个旋轮绕芯模轴线的公转运动和沿轴向的进给运动。模具与变形体的接触条件采用罚函数接触算法,并定义旋轮与工件外表面的摩擦因数为0.05,芯模与工件内表面的摩擦因数为0.2。建立的带螺旋内筋薄壁筒形件旋压有限元模型如图2所示,旋轮的运动轨迹为右旋加载轨迹,因此定义右旋筋槽为同向筋槽,在同向筋槽内成形的螺旋内筋为同向筋,定义左旋筋槽为反向筋槽,在反向筋槽内成形的螺旋内筋为反向筋。其余主要旋压参数为:旋轮压下量3 mm,主轴转速120 r/min,进给比1.6 mm/r。

图2 带螺旋内筋薄壁筒形件旋压有限元模型Fig.2 FE model for flow forming of thin−walled tube with helical grid−stiffened ribs
1.2 模型可靠性验证
带螺旋内筋薄壁筒形件旋压成形过程中工件的动能与内能之比如图3所示。由图可知,成形过程中工件的动内能比值始终在10%以下,这表明旋压成形模拟结果是符合准静态变形的要求,由此可以认为本文所建立的带螺旋内筋薄壁筒形件旋压有限元模型是稳定的。

图3 旋压过程工件动能与内能比值变化Fig.3 Kinetic energy/internal energy for workpiece during flow forming process
带螺旋内筋薄壁筒形件旋压有限元仿真与实验螺旋内筋在不同截面的充填情况如图4所示。由图可知,有限元仿真获得的轴向不同位置同向筋高与反向筋高的关系与实验结果完全一致,由此表明本文所建立的带螺旋内筋薄壁筒形件旋压有限元模型是可靠的。
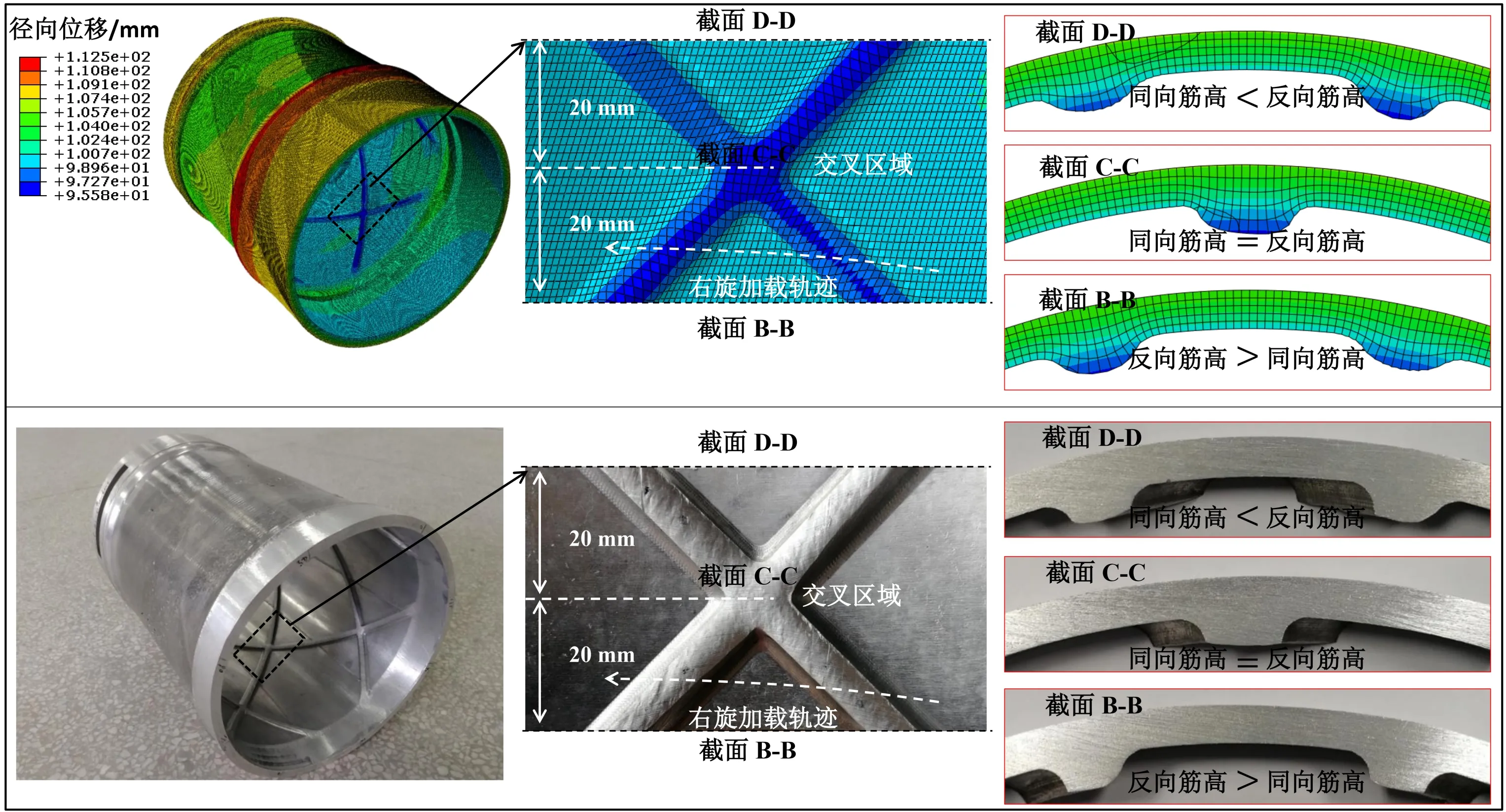
图4 仿真与实验充填效果对比[12]Fig.4 Comparison of rib−filling result between FE simulation and experiment[12]
2 结果与讨论
2.1 应力分布特征
如图5所示为旋压成形过程中旋轮分别作用在同向筋、筒壁区和反向筋时的应力分布情况。由图可知,当旋轮作用在筒壁区时,内外层材料的应力状态一致,均为三向压应力状态。而当旋轮作用在同向筋和反向筋处时,由于筋槽的存在,内外层材料的应力状态存在明显的差异。同向筋和反向筋外层材料的应力状态为三向压应力状态,内层材料径向受压应力,切向和轴向受拉应力。
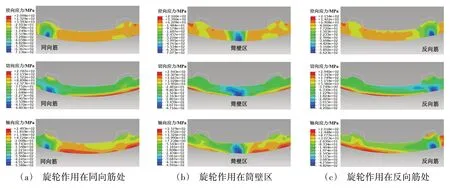
图5 旋轮作用下不同区域的应力分布图Fig.5 Stress distribution when the roller rotates at different regions
2.2 应变分布特征
图6(a)为工件成形后整体的等效塑性应变分布云图,从图中可以看出,旋压成形后工件应变分布不均匀:工件外层材料的应变大于内层材料的应变,这是因为旋压成形过程中材料的变形主要发生在工件外层;同时,筒壁区材料的应变普遍大于内筋区材料的应变。为了定量分析不同区域应变的变化规律,选取如图6(b)所示内层、中间层、外层3 条路径,获得了3条路径上单元的等效塑性应变的分布规律,如图6(c)所示。由图可知,外层单元的等效塑性应变最大,中间层次之,内层单元的等效塑性应变最小。内筋处外层、中间层和内层单元的应变均有明显的下降趋势,在内筋圆角区域内层单元的等效塑性应变有极大值。

图6 带螺旋内筋薄壁筒形件等效塑性应变分布Fig.6 Distribution of equivalent plastic strain in flow forming of thin−walled tube with helical grid−stiffened ribs
不同区域材料的径向、切向和轴向应变分布情况如图7所示。由图7(a)可以看出,工件的筒壁区材料沿径向产生压缩应变,且外层材料的压缩应变大于内层材料,这是因为材料变形主要发生在筒壁外层。靠近内筋区域,材料受到径向压缩的变形量开始逐渐减小。在内筋处,由于材料沿径向充填内筋,其径向应变由外层材料的压缩应变逐渐演变为内层材料的拉伸应变。不同区域材料的切向应变如图7(b)所示,筒壁区材料沿切向为拉伸应变,而内筋处材料沿切向为压缩应变。对比不同区域材料的轴向应变可知,筒壁区和同向筋处始终为轴向拉伸应变,而反向筋处的轴向应变绝对值相对较小,部分区域为轴向拉伸应变,部分区域为轴向压缩应变。
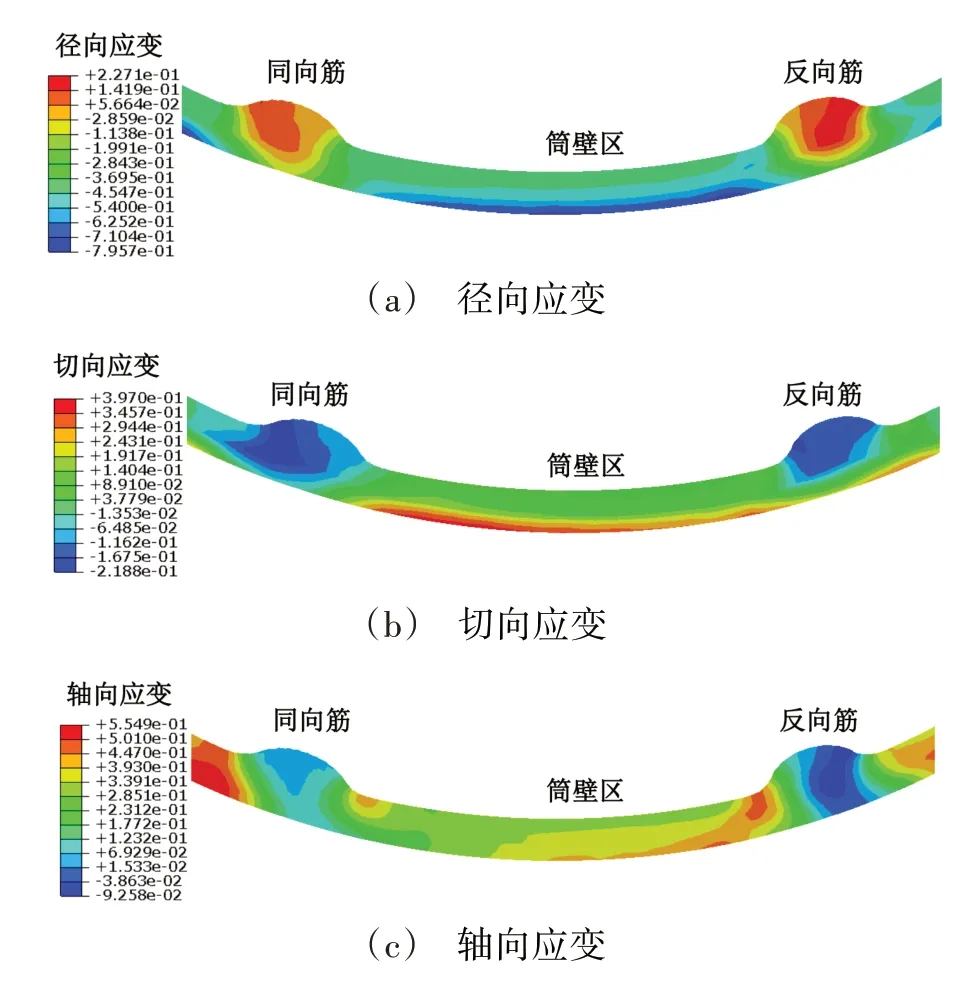
图7 成形工件不同区域应变分布Fig.7 Strain distribution at different regions of formed tube
3 结论
(1)带螺旋内筋薄壁筒形件旋压过程中筒壁区内外层材料在旋轮作用下受三向压应力,而内筋处由于筋槽的存在,其内外层材料在旋轮作用下存在明显的应力状态差异,外层材料受三向压应力,内层材料径向受压应力,切向和轴向受拉应力;
(2)带螺旋内筋薄壁筒形件旋压成形后不均匀变形特征显著,外层材料应变大于内层材料应变,筒壁区材料应变大于内筋区材料应变;
(3)筒壁区的应变特征为径向压缩应变,切向和轴向为拉伸变形,而内筋区的应变特征主要为外层材料的径向压缩应变逐渐演变到内层材料的径向拉伸应变。

