基于Geo-Studio和MIDAS GTS NX的边坡稳定性分析

叶 武，张 政，杨国镁

（浙江海川勘察有限公司，浙江杭州310000）

工程建设所产生的人工边坡，需在稳定性评价的基础上，预判边坡失稳的可能性，根据边坡等级所确定的安全系数值计算下滑力，为边坡治理设计提供依据。边坡稳定性评价方法分为定性分析和定量计算两类，前者如工程类比法[1]和赤平极射投影图分析等图解法，后者主要包括基于极限平衡理论的Felenius法、Morgenstern-Price法、Spencer法、Bishop法和Janbu法；数值分析法中的有限单元法FEM、边界元法BEM[2]、离散元法DEM[3]等；可靠度分析方法中的蒙特卡罗法和随机有限元法等，以上分析计算方法均得到有效的应用。由于边坡地质环境条件复杂程度不等，除岩土体本身的工程地质条件外，还包括受地质构造因素、节理裂隙发育特征、水文地质条件以及施工方法、扰动等众多因素综合影响，各影响因素又具有复杂性和不确定性[4]，因此计算分析结果不一定与实际非常吻合,各种计算方法有不同的适用条件最终计算结果也会不同。

1 边坡稳定性分析方法

1.1 极限平衡法

应用静力平衡原理，将可能失稳的边坡滑体离散成土条，通过一定的条间力简化假设条件，根据试选的滑动面,以单位宽度的分块滑体为分析单元，将总的下滑力与沿滑动面可能提供的总抗剪强度（抗滑力）比值作为安全系数，滑动面s（总抗剪强度）与σ（作用在滑面上的垂直应力）存在如下关系：s=c+σ·tanφ。极限平衡法可分为简化法和严格条分法两类，简化法仅满足条间法向力，或剪切力平衡，或仅满足力矩平衡，严格条分法同时满足条间力和力矩平衡[5]，尽管极限平衡法存在内在的物理学缺陷，但作为整体下滑力和抗滑力整合平滑后整个滑体的安全系数十分合理和真实，是边坡工程分析中应用最为广泛的一种方法。

（1）瑞典条分法（Felenius法）。不考虑滑动土体条间法向力(E)、剪切力(X)，不满足力平衡条件，满足基于某一点的所有力矩之和平衡条件，实际应用中由于计算结果偏于安全（低10%～20%），所以在工程上应用较广。

（2）简化毕肖普法（Bishop法）。考虑土条间法向力，不考虑土条间剪切力，建立基于垂直方向静力平衡的条块底部法向力方程，安全系数公式：

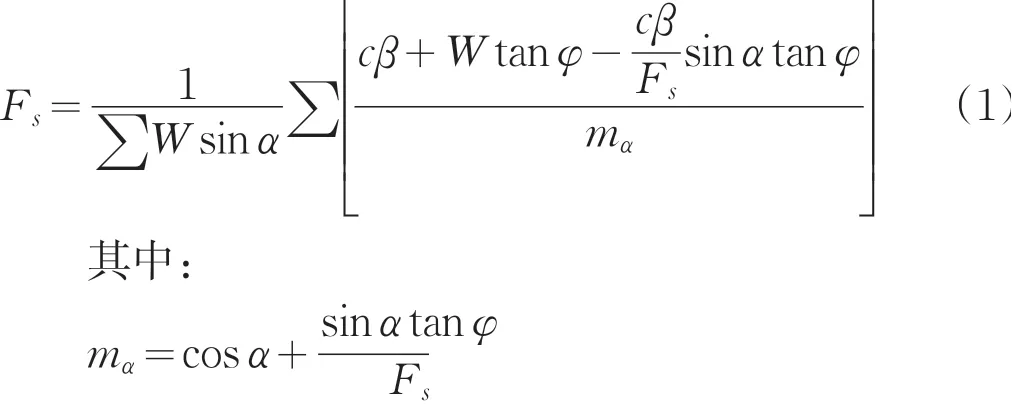
Fs初始值可取瑞典条分法计算得出的安全系数，计算出mα，然后计算稳定系数Fs，迭代重复计算至前后二次的Fs的差值至允许的精度范围。

（3）简化简布法（Janbu法）。不满足所有的力矩平衡条件，满足水平力的平衡条件，因条间剪切力对力的平衡影响较大，而本方法忽略了土条间的剪切力，导致计算所得安全系数偏低。

（4）Spencer法。满足条间法向力平衡和力矩平衡，假定条间剪力和法向力(E)比值为定常系数λ，通过迭代过程，以不同λ值为横坐标，分别计算出基于整体力矩平衡、基于条间法向力平衡对应安全系数的拟合曲线，力和力矩平衡曲线的交点纵坐标即为安全系数。该方法力矩平衡和法向力的平衡均能满足，但不满足剪力的平衡，由此当滑裂面顶部存在侧向力时，稳定系数计算结果的精度相对较低，实际工程应用将带来安全隐患[6]。

（5）Morgenstern-Price法。考虑了条间法向力和剪切力，假定两者之间呈函数关系X=Eλf(x)，条间力函数f(x)形式例如常量（即退化为Spencer法）、半正弦、梯形等，对参数λ、f(x)和稳定系数Fs赋初始值进行迭代计算，类似Spencer法，力和力矩平衡曲线的交点纵坐标即为安全系数。

1.2 有限元法

有限元法是将连续几何结构离散成有限个单元，每个单元设定有限个节点，对每个单元假定合适的近似解，计算精度随着单元划分的不同而不同，划分越细计算精度越高，但计算量越大，是目前应用最广泛的数值方法[7]。有限元法把岩土体作为变形体，按照岩土体的本构模型，建立单元刚度矩阵、总体刚度矩阵，从而求得节点位移分量、内力和应力，然后再根据M-C强度准则，计算评价边坡的整体稳定性。

1.2.1 强度折减法

将岩土材料的抗剪强度参数c和tanφ，除以折减系数得以降低抗剪强度，折减系数的初始值取得足够少，以保证开始时是一个近乎弹性的问题，用降低的抗剪强度参数进行计算，按一定的步长，通过不断降低抗剪强度参数，即逐渐增加抗剪强度的折减系数，直至计算不收敛，将此时的折减系数Fs定义为边坡的稳定系数。

式中：c、φ——岩土体的抗剪强度参数；

cf、φf——折减后的强度参数；

Fs——强度折减系数。

1.2.2 强度折减法边坡失稳的判据

边坡失稳的实质是强度破坏，目前关于有限元强度折减法分析边坡失稳的判据[8]之一是数值计算过程不收敛；之二以剪切塑性应变从坡脚至坡顶贯通为判据；之三以坡体或坡面特定点的突变特征或变形趋势分析判断。

关于边坡失稳的判据目前仍尚未形成统一的标准，判据之一的数值计算过程不收敛作为失稳判据有所欠缺，将前后计算值的比值小于10-3作为收敛性标准具有一定的主观性。判据之三的坡体或坡面位移突变仍属不收敛性范畴。本文以广义塑性应变或者等效塑性应变作为评判指标，将塑性区的范围及塑性区从坡脚到坡顶贯通作为边坡失稳的标志[9]。

2 工程应用

2.1 工程概况

富阳市富春街道西山坎区块场地由东向西呈台阶状布置，东侧场地设计高程为26.00m，往西各级平台高程分别为30.70m、34.70m、38.40m，至西侧拟开挖形成边坡脚高程为42.60～43.38m，将形成一条长约500m、高约30～50m人工边坡。边坡区基岩岩性为志留系中统康山组深灰色、青灰色细砂岩，地层产状310°～335°∠45°～55°，表层土体为含碎石粉质粘土，边坡位于抗震设防烈度6度区。

2.2 极限平衡法计算

含碎石粉质粘土和全风化细砂岩开挖坡率（1∶1.0）～（1∶1.25），强风化细砂岩开挖坡率（1∶0.75）～（1∶1.0），中风化细砂岩坡率（1∶0.5）～（1∶0.75），涉及边坡岩土体的物理力学参数确定见表1。

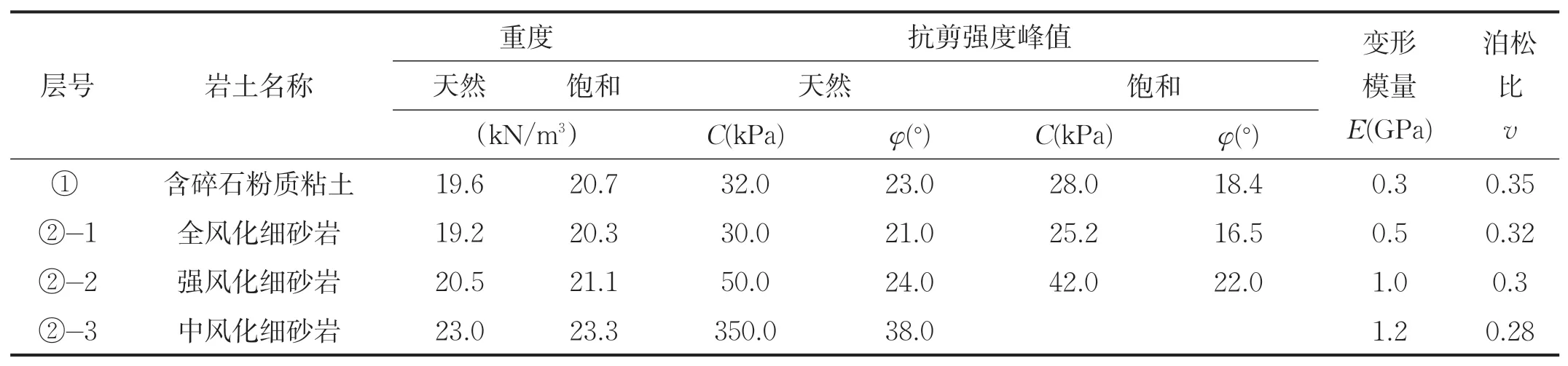
表1 岩土体的物理力学参数建议值

2.2.1 计算滑动面分析

开挖边坡出露岩土体主要为全风化—强风化细砂岩体，综合分析认为滑裂面位于全风化—强风化细砂岩体内部。

2.2.2 边坡稳定性计算

应用SLOPE/W内嵌的瑞典条分法、M-P法、Spencer法、Bishop法、Janbu法，在天然工况和暴雨工况下，试算不同滑动面对应的安全系数，确定最不利滑动面、最小安全系数作为边坡的稳定系数。图1列出4种计算结果图，表2列出各计算所得稳定系数。

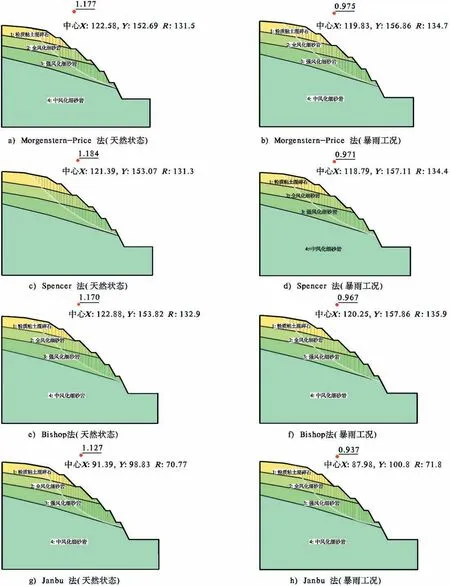
图1 不同工况下4种计算方法结果

边坡等级定为一级边坡，天然工况下要求安全系数达1.35以上，暴雨工况要求达1.05以上。

根据计算结果（表2），Felenius法计算的安全系数值最小，这是因为此种方法不考虑土条间的作用力，因此作为稳定性评价计算结果偏于安全，各方法计算结果值差别小，说明这些方法对于本边坡的计算均是合适的，其中的M-P法、Spencer法和Bishop法计入了条间推力，此3种方法计算的稳定系数更符合实际情况。暴雨工况下较天然工况小20%左右，可见地下水对边坡稳定性影响是比较大的。

表2 5种计算方法稳定系数对比

2.3 有限元法

与极限平衡法的地质剖面相同，利用CAD剖面图导入建立二维有限元几何模型，定义各种材料后进行有限元网格划分，由于有限元法计算精度主要受网格密度和网格质量控制，按四边形网格共划分6921个单元，27415个结点，尽可能保持高应力梯度区域网格的质量，而后进行网格质量的检查。材料定义中的抗剪切强度参数与极限平衡法相同，见表1，屈服准则采用D-P屈服准则，经加载、约束条件设置后求解。

图3 剖面等效应变云图

采用强度折减法（SRM）分析，图2～图5显示天然工况下边坡体的合位移云图、等效应变云图、第一主应力、第三主应力分布特征。根据数值模拟结果，计算得到的稳定系数值为1.216，以塑性区贯通作为边坡失稳判据所得稳定系数与极限平衡法的差别较小。

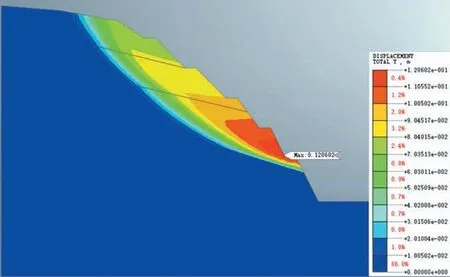
图2 剖面合位移云图

图4 第一主应力云图

图5 第三主应力云图

2.4 对比分析

经对极限平衡法和有限元法这二种方法的计算结果分析可以得出：

（1）Felenius法、M-P法、Spencer法、简化Bishop法和简化Janbu法均基于极限平衡理论，滑动土体为刚性体，而不考虑滑动体本身的应力—应变关系，满足水平力、或垂直力、或力矩平衡中的一个、多个或全部的平衡方程进行分析，5种方法最大的不同之处在于条间法向力、剪切力的假定差异，从而造成计算结果不同。

（2）同一工程实例这二种方法计算得出最不利滑动面圆心的平面位置和圆弧半径相接近，稳定系数也相接近，有限单元强度折减法计算得到的稳定系数值为1.216，略高于极限平衡法（其中最大值为Spencer法的1.784），分析认为由于各种极限平衡法均对条间力进行了一定简化、假定，选用确定的，或线性变化的参数参与计算，与实际情形有一定的差异，对计算精度造成一定的影响，为两者形成差值的其一原因；而综合考虑了土体的应力—应变关系的有限元强度折减法，真实模拟了开挖后的边坡体在岩土体自重力作用下内部应力应变的变化的过程，显示的是塑性发展变形情况，至坡顶贯通后即为最不利滑动面，更符合实际情形，从而较极限平衡法略高。

3 结论和讨论

计算结果表明各种方法所得稳定系数较接近，最不利滑动面的位置和几何形状较相似，均可作为设计的依据，而M-P法、Spencer法和Bishop法计算的稳定系数更符合实际情况，实际工程应用中应采取如M-P法、Spencer法等严格条分法进行边坡稳定性分析。

分析软件SLOPE/W建模后定义材料特性，综合分析确定滑动面滑入范围与滑出范围后进行计算分析，前处理过程简单，内嵌各模块计算结果精度满足工程需求，对大部分边坡稳定性问题能进行有效计算和分析。

有限元法不需判断假定滑动面的位置，采取模拟边坡渐近破坏方式，以破坏判据得出稳定系数计算结果，由于考虑了边坡土体的应力—应变关系，更符合实际情形，使得有限元强度折减法在边坡稳定性分析中得到更广泛的应用。