一种基于束缚态的可调等离子体光子晶体窄带滤波器*

周铭杰 谭海云 周岩 诸葛兰剑 吴雪梅†

1) (苏州大学物理科学与技术学院, 苏州纳米科技协同创新中心, 苏州 215006)

2) (江苏省薄膜材料重点实验室, 苏州 215006)

3) (苏州大学光电科学与工程学院, 苏州 215006)

4) (苏州大学分析测试中心, 苏州 215123)

利用一维光子晶体和二维等离子体光子晶体构建了一种基于束缚态的可调窄带滤波器, 滤波器的工作频率位于两个光子晶体的共同禁带内.使用COMSOL Multiphysics有限元仿真软件研究了一维光子晶体的几何参数和等离子体参数对滤波器性能的影响.研究发现两个禁带的中心频率和深度越接近, 则滤波器的峰值透射率越大, 且中心频率占主导作用.另一方面, 滤波器的工作频率与等离子体密度成正比, 与碰撞频率成反比.滤波器品质因子和峰值透射率随等离子体密度的增大先增大后减小, 随碰撞频率的增加而减小.最后,随着等离子体碰撞频率的增加, 峰值透射率和品质因子没有发生显著下降, 这表明滤波器对等离子体损耗有一定抵抗力.我们相信这项工作有助于一些新型等离子体光子晶体滤波器的研究.

1 引 言

光子晶体（photonic crystals, PCs）自提出以来引起了人们的广泛关注[1,2].人们基于PCs对电磁波的调控能力提出了许多应用.例如光子晶体光纤[3]、光子晶体滤波器[4]、光子晶体波导[5]和光子晶体天线[6]等.其中, 光子晶体滤波器[7,8]是一种具有信号频率选择功能的器件, 其在微波通信领域得到广泛的研究[9−12].一般而言, 可调光子晶体滤波器是一种波导-谐振腔-波导结构[4].通过在谐振腔中填充折射率可调介质, 例如液晶[13]和热敏材料[14], 滤波器可以获得一定的调谐能力.值得注意的是, Wang等[15]在谐振腔中添加等离子体, 并研究了等离子体参数对滤波器的影响, 利用实验证实了等离子体光子晶体（plasma photonic crystals,PPCs）滤波器是一种可调滤波器.

谐振腔滤波器对腔的结构非常敏感, 在腔中引入扰动会影响滤波器性能.对此, 基于束缚态的滤波器可能是一种解决方案.研究表明, PCs存在一种与光子晶体拓扑性质有关的束缚态[16], 其对扰动不敏感.严格来讲, 调节PCs使带结构发生反转, 带隙的拓扑性质会发生变化[17].如果将两种拓扑性质不同的带隙材料拼接在一起并保证两者存在公共带隙, 则交界面可能存在局域的束缚态, 透射谱的禁带区域会出现一个透射峰.这种伴随高透射率的束缚态具有高度鲁棒性, 其电磁性质对界面附近的扰动不敏感.

基于上述研究基础, 本文设想了一种基于光子晶体束缚态的窄带滤波器, 并利用等离子体使滤波器获得动态可调能力.本文同时研究了影响滤波器性能的因素, 讨论了等离子体参数对峰值透射率和品质因子的影响.研究发现该滤波器对等离子体损耗不敏感, 这与填充等离子体的谐振腔滤波器不同.

2 滤波器模型及机理分析

本文所设想的滤波器模型如图1所示, 其由位于 x oy 平面的两块PCs构成, 两个PCs相交于红色虚线处.左侧为氧化铝在空气中的周期堆叠, 晶格常数为 L , 周期数量为 N1, x 方向总长为 N1L ,氧化铝的相对介电常数和厚度分别为8.9和 d.右侧是空气中放电管的长方晶格, x 方向和 y 方向的晶格常数分别为 ax和 ay, x 方向总长度为 N2ax,N2表示 x 方向的周期数量.放电管由等离子体和石英环组成, 其中, 石英环的相对介电常数和厚度分别为3.7和 ( r2−r1) , r1表示等离子体半径, r2为石英柱半径.等离子体的相对介电常数为[18]

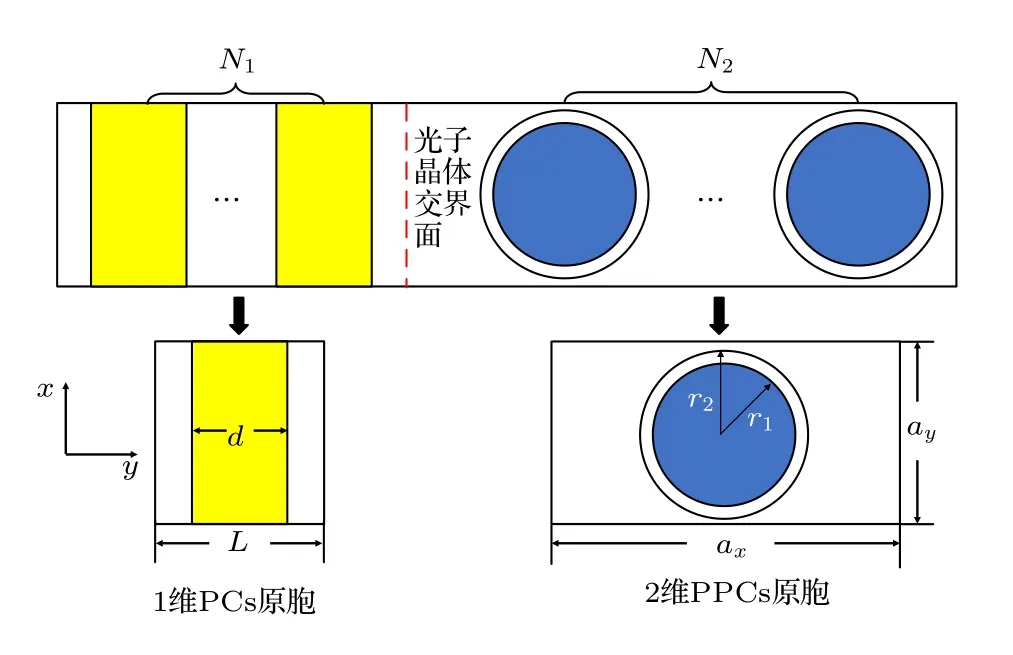
图1 滤波器示意图, 下图展示了两种光子晶体的原胞Fig.1.Schematic diagram of the filter.The figure below shows the unit cells of two photonic crystals.

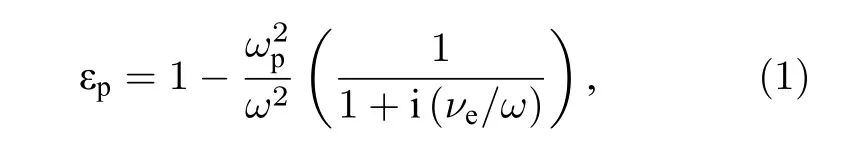
其中, ZL和 ZR分别表示左侧和右侧光子晶体的表面阻抗.PCs的有效阻抗 Zeff可以表示为Zeff=在公共带隙内, 如果两种PCs的εeff异号, 就可能满足条件 ZL+ ZR=0.文献[19, 20]则指出, 两种PCs的 εeff异号就是指两种PCs带隙的拓扑性质不同.因此, 束缚态依赖两个拓扑性质不同的光子带隙.

若要改变带隙的拓扑性质, 需要调节PCs参数让带隙先关闭再打开, 使得上下能带发生交换[17,20].对于放电管构成的PPCs, 可以调节等离子体密度使次序为 n （ n 为大于0的正整数）的带隙关闭, 然后增加等离子体密度重新打开带隙[21].图2展示了调节过程, 其中, 2维 (2D) PPCs参数为ax=40mm , ay=12mm , r1=4mm , r2=5mm ,N2=10, νe=0.计算中取 n =1.本文利用有限元仿真软件COMSOL对模型进行数值计算.

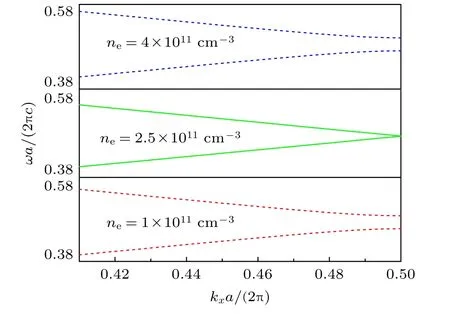
图2 随等离子体密度增加, 2D PPC的1阶带隙经历了从关闭到再打开的过程Fig.2.As the plasma density increases, the first-order band gap of 2D PPC undergoes a process from closing to reopening.

从图2中可以看出, 随等离子体密度增加, 带隙经历了从关闭到再打开的过程.这种现象与波阻抗有关[22].详细地说, 调节等离子体密度可以让石英放电管的有效阻抗和背景介质的阻抗相等, 从而关闭带隙.进一步增大等离子体密度会破坏阻抗匹配条件, 从而打开带隙.带隙从关闭到重新打开的过程就是上下能带交换的过程, 带隙的拓扑性质因此发生变化.

在图1所示模型中, 首先调节等离子体密度ne使2D PPCs的1阶带隙先消失再重新打开, 再调节1D PCs参数以确保两者的1阶带隙重合, 从而获得束缚态.图3展示了调节过程, 其中, 图3(a)和图3(b)分别表示1D PCs和两种2D PPCs的能带图, 图中均以黄色区域表示公共带隙, 两者的区别在于图3(b)中2D PPCs的带隙是重新打开的带隙.图3(c)表示上述两种情况下的透射谱, 图3(d)表示束缚态在滤波器中的场分布.在计算中, 1D PCs的参数为 L =20mm , d =0.45L , N1=3.2D PCs的 参 数 为 ax=40mm , ay=12mm ,r1=4mm , r2=5mm , N2=10 , νe=0.对 于 图3(a),ne=0.对于图3(b), ne=6×1011cm−3.

图3(a)和图3(b)表明两种2D PPCs的带隙均和1D PCs的带隙有所重合.但图3(c)表明, 仅当2D PPCs的带隙性质发生变化后, 滤波器才能进行工作.从图中可以看出, 当 ne=0 时, 透射谱中没有出现透射峰.相比较而言, 当ne=6×1011cm−3时, 因为2D PPCs的1阶带隙经历了先关闭再打开的过程, 带隙性质发生了变化, 所以透射谱中出现了一个尖锐的透射峰, 其位于约4.078 GHz处,峰值透射率接近100%.透射峰的位置与束缚态的阻抗条件有关, 其一定位于公共带隙内.从图3(d)可以看出, 束缚态集中在光子晶体交界面附近, 距离交界面的距离越远, 电场强度也越小.有趣的是,电场主要局域在2D PPC表面而非1D PC表面,并且其在PPC内衰减得更慢.

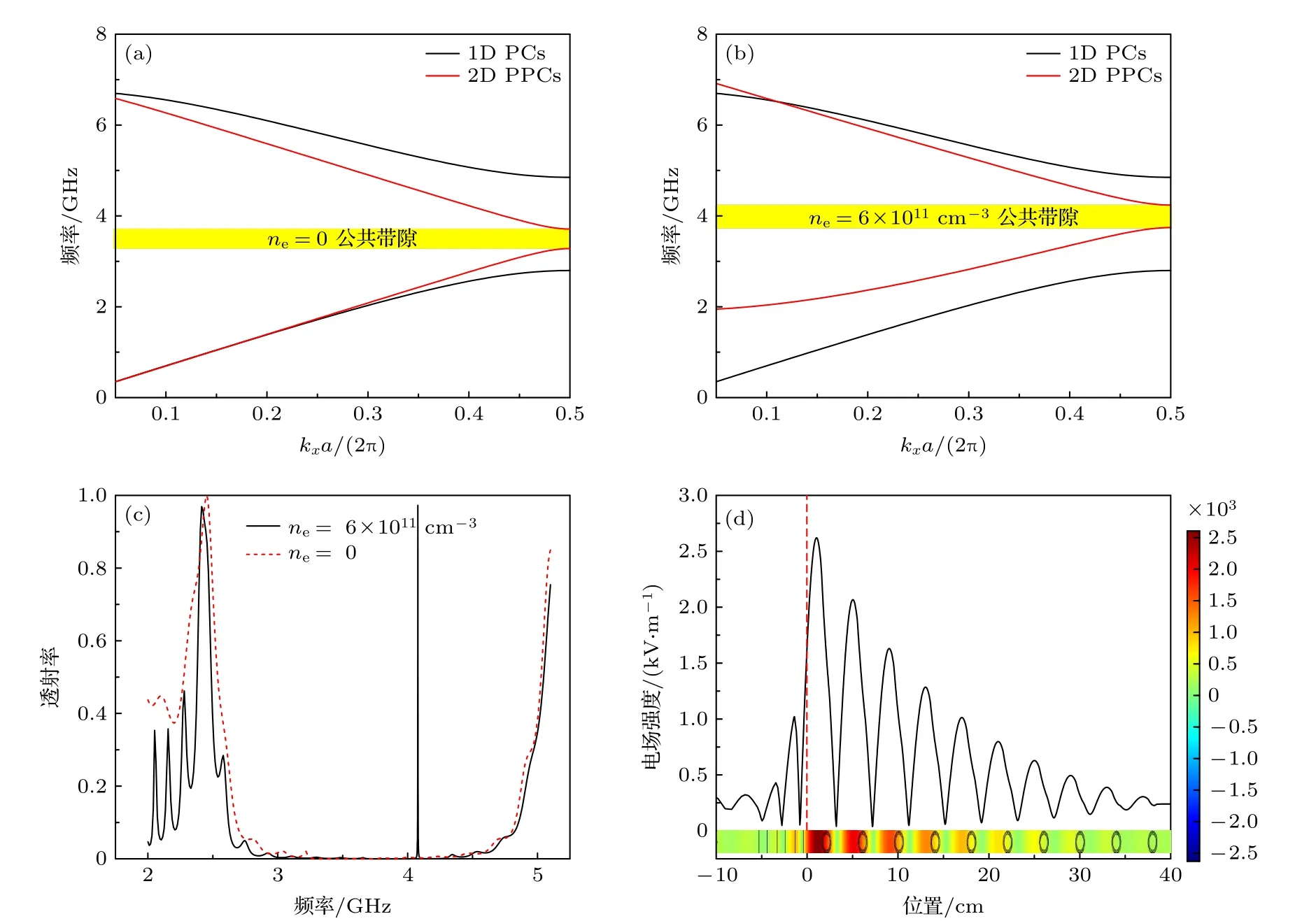
图3 (a) n e=0 时两种光子晶体的能带图; (b) n e=6×1011cm−3 时两种光子晶体的能带图; (c) n e=0 和ne=6×1011cm−3时滤波器的透射谱; (d) 电场强度沿模型边界的线分布, 其中, 插图表示滤波器中的电场分布Fig.3.(a) Band structure of two different PCs with n e=0 ; (b) band structure of two different PCs with n e=6×1011cm−3 ; (c) transmission spectrum of the filter when n e=0 and n e=6×1011cm−3 ; (d) the intensity of electric field along the line of the model boundary, where the inset shows the electric field distribution in the filter.

3 影响滤波器性能的因素

根据(2)式, PCs的有效阻抗可以影响滤波器性能, 而有效阻抗与PCs的光学参数与周期数量有关.本节将研究这些参数对滤波器性能的影响.

3.1 1D PCs参数的影响

首先研究1D PCs参数对滤波器性能的影响,图4(a)和图4(b)分别表示滤波器透射谱随1D PCs周期数和氧化铝厚度的变化情况.在计算中,2D PPCs参数不变, 即 ax=40mm , ay=12mm ,N2=10 , ne=6×1011cm−3, νe=0.与 此 同 时,保持1D PCs的周期长度 L =20mm 不变.在图4(a)中, 氧化铝厚度 d 为 0.45L , 在图4(b)中, 1D PCs周期数N1=3.

从图4(a)可以看出, 约4.08 GHz附近存在一个透射峰.随着周期数量 N1增大, 透射峰的中心频率有微小变化.此外, 峰值透射率先增大后减小,当 N1=3 时, 峰值透射率达到最大.在图4(b)中,随着氧化铝厚度 d 增大, 透射峰的中心频率向低频移动, 峰值透射率先增大后减小.图4表明存在一个最佳1D PCs参数.

研究发现禁带匹配度可以衡量1D PCs参数对滤波器的影响.禁带匹配度由禁带深度（以透射率为单位）和禁带的中心频率进行表征.定义中心频率匹配度 ∆f为禁带深度匹配度 ∆s为其中, f1和 s1分别是1D PCs的禁带中心频率和禁带深度, f2和 s2分别是2D PPCs的禁带中心频率和禁带深度,图5展示了禁带匹配度随1D PCs参数的变化情况, 其中, 图5(a)展示了禁带匹配度与 N1的关系,图5(b)展示了禁带匹配度与 d 的关系.可以看到,禁带匹配度随1D PCs参数不断变化, 并且当禁带匹配度最大时, 峰值透射率最高.例如在图5(a)中, 当 N1=3 时, ∆f=98% , ∆s=77.6% , 两者均为最大值, 而在图4(a)中, N1=3 可以获得最大的峰值透射率.因此, 匹配度越大, 峰值透射率越大, 该规律在图5(b)中同样存在.有趣的是, 研究发现峰值透射率更依赖 ∆f.例如在图5(b)中, 当 d /L 分别为0.35和0.55时, 前者的 ∆s较小但 ∆f更大.而在图4(b)中, d /L=0.35 可以获得更大的峰值透射率.

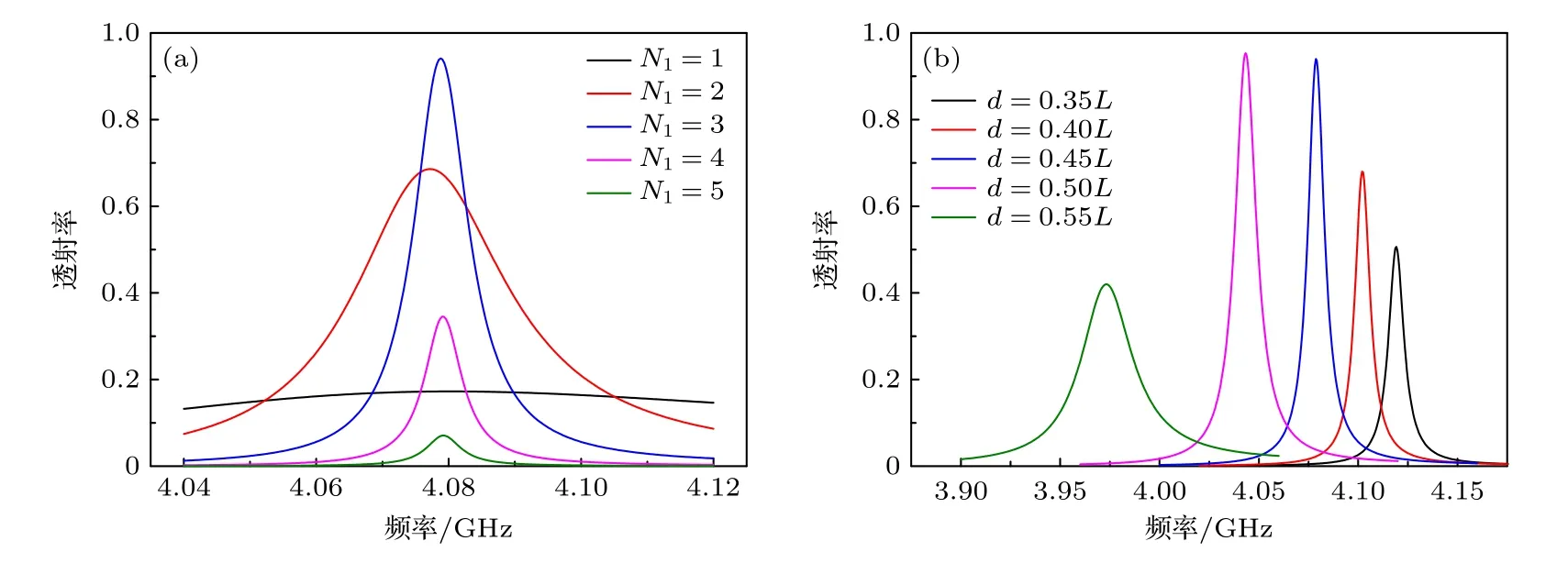
图4 (a)滤波器透射谱与 N 1 的关系; (b) 滤波器透射谱与d的关系Fig.4.(a) The relationship between the transmission spectrum of the filter and N 1 ; (b) the relationship between the transmission spectrum of the filter and d.

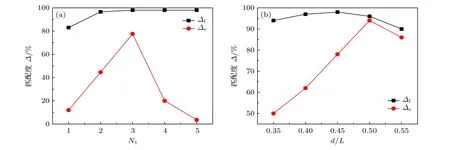
图5 (a)禁带匹配度与 N 1 的关系; (b)禁带匹配度与 d 的关系Fig.5.(a) The relationship between the band gap matching degree and N 1 ; (b) the relationship between the band gap matching degree and d.

3.2 等离子体密度的影响

为了进一步研究滤波器的性能, 图6展示了等离子体密度 ne对滤波器性能的影响.其中, 图6(a)表示滤波器透射谱与 ne的关系, 图中还以点线表示透射峰中心频率随 ne的变化情况.图6(b)表示滤波器峰值透射率和品质因子Q与 ne的关系, 其中,品质因子Q定义为[16]：

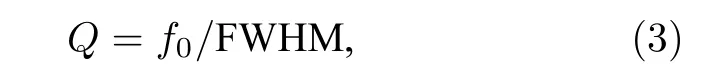
其中, f0表示透射峰的中心频率, F WHM 表示透射峰的半高宽.定义 T0为透射峰的峰值透射率.在计算中, 1D PCs的参数为 N1=3 , L =20mm ,d=0.45L.2D PPCs的参数为 N2=10 , ax=40mm ,ay=12mm , r1=4mm , r2=5mm , νe=0.

从图6(a)可以看出透射峰中心频率对 ne十分敏感.随着 ne增加, 滤波器中心频率向高频移动.增大 ne会降低等离子体的介电常数, 使禁带中心频率上升[23].因此, 改变 ne会影响2D PPCs的禁带中心频率并对透射峰位置进行调制.

从图6(b)可以看到, 随 ne增加, 峰值透射率先增加再减小, 拐点出现在 ne=6×1011cm−3处.这种现象与禁带匹配度的变化有关.另一方面, Q值同样随 ne先增大后减小.有趣的是, Q值的拐点位置与峰值透射率的拐点位置并不相同, Q值的拐点出现在 ne=7×1011cm−3处.这说明滤波器Q值与峰值透射率没有必然联系.

3.3 等离子体碰撞频率的影响

最后研究等离子体碰撞频率 νe对滤波器性能的影响, 计算结果如图7所示.其中, 图7(a)表示滤波器透射谱与 νe的关系, 图中还以点线表示透射峰中心频率随 νe的变化情况.图7(b)表示滤波器峰值透射率和品质因子与 νe的关系.在计算中,ne=6×1011cm−3, 其余参数与图6一致.

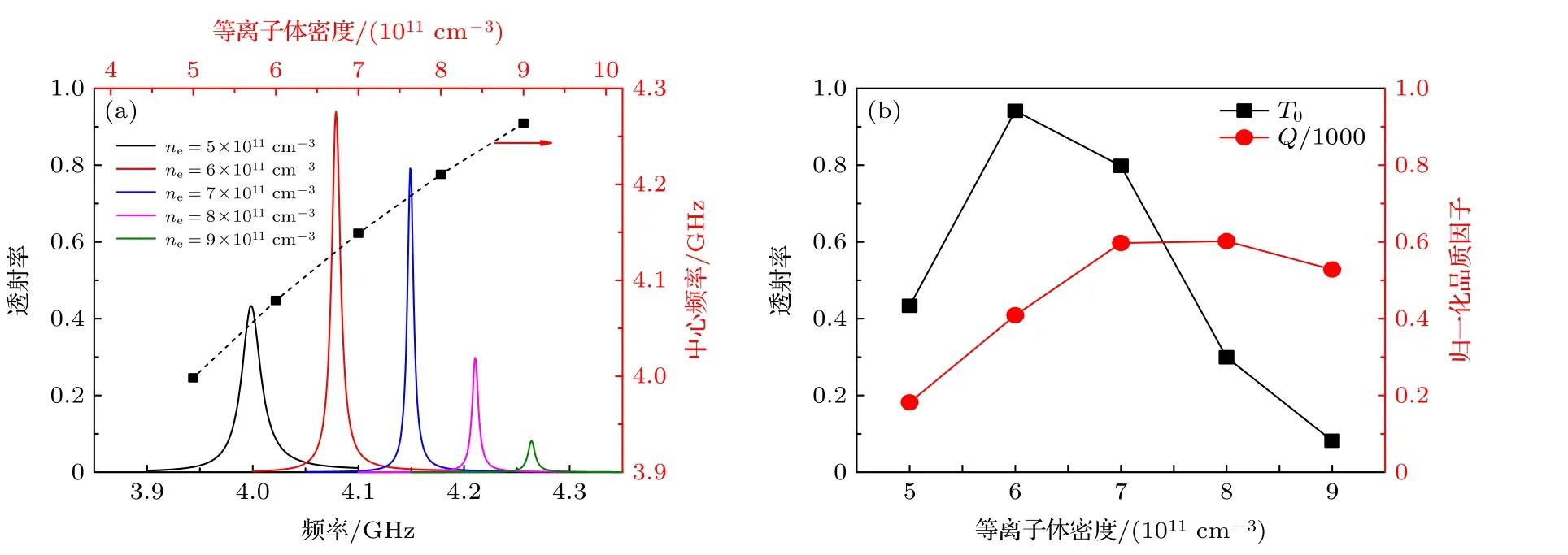
图6 (a) 滤波器透射谱与 ne 的关系, 点线表示滤波器的中心频率随 ne 的变化; (b) 滤波器峰值透射率以及品质因子与 ne 的关系Fig.6.(a) The relationship between the transmission spectrum of the filter and ne , while the dotted line shows the evolution of the center frequency of the filter with ne ; (b) the relationship between the peak transmittance of the filter as well as the quality factor and ne.

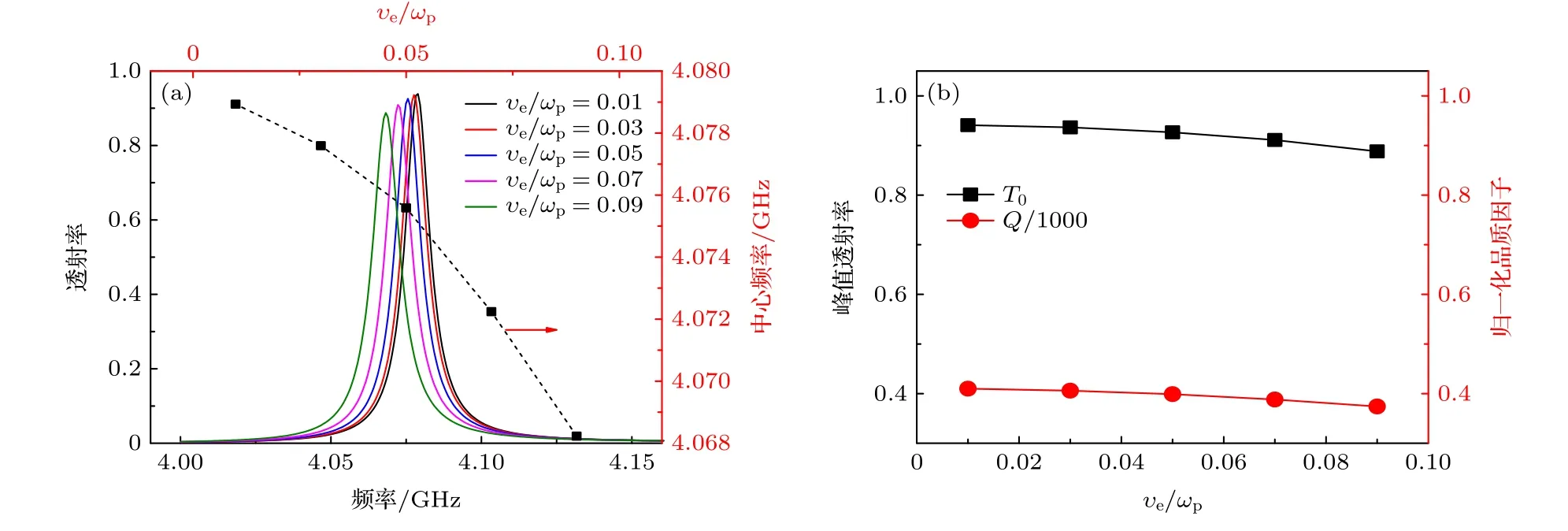
图7 (a) 滤波器透射谱与 νe 的关系, 点线表示滤波器的中心频率随 νe 的变化; (b) 滤波器峰值透射率以及品质因子与 νe 的关系Fig.7.(a) The relationship between the transmission spectrum of the filter and νe , while the dotted line shows the evolution of the center frequency of the filter with νe ; (b) the relationship between the peak transmittance of the filter as well as the quality factor and νe.

从图7(a)中可以看到, 当 νe增加时, 透射峰中心频率向低频移动, 这是因为增加 νe会增大等离子体介电常数的实部项, 使2D PPCs的禁带中心频率红移.另一方面, 从图7(b)可以看出峰值透射率和品质因子Q随 νe的增加而不断减小, 但下降幅度很低.比如, 当 νe/ωp从0.01增加到0.09时, 峰值透射率从0.9385下降到0.8875, 下降幅度约为5.4%; 品质因子从410下降到374, 下降幅度约为8.78%.这说明本文所提出的滤波器对碰撞频率不敏感, 其与填充等离子体的谐振腔滤波器明显不同[24].这种现象与本文所提出滤波器的原理有关.在这里, 滤波器的窄带高透射率现象依赖局域的束缚态, 其电场几乎集中在两种PCs之间的空气区域, 仅有一少部分“渗透”进入有损等离子体.因此,等离子体损耗对滤波器的性能影响较低.

4 总 结

本文提出了一种基于束缚态的光子晶体滤波器.通过引入等离子体, 滤波器有一定的可调能力.研究表明, 通过调节等离子体密度, 使得2D PPCs的禁带消失再重新打开, 再调节1D PCs的参数使得两个光子晶体的禁带重合, 便可以在禁带区域内获得窄带透射峰.滤波器的性能与两个PCs的禁带匹配度有关, 并且禁带匹配度越好, 峰值透射率越高.与此同时, 该滤波器对等离子体密度较为敏感.调节等离子体密度可以调节滤波器中心频率和品质因子, 且两者均随着等离子体密度的增大先增大后减小.最后, 本文提出的滤波器对等离子体碰撞频率不敏感, 在低温等离子体的范畴内, 增加碰撞频率对滤波器性能几乎没有影响.