NiCu双金属纳米粒子的表面偏析、结构特征与扩散*
邓永和 张宇文 谭恒博 文大东 高明 吴安如
1) (湖南工程学院计算科学与电子学院, 湘潭 411100)
2) (吉首大学物理与机电工程学院, 吉首 416000)
3) (湖南工程学院, 湖南省汽车动力与传动系统重点实验室, 湘潭 411104)
NiCu双金属核壳纳米粒子不仅由于其优异的稳定性、选择性以及磁学和催化性能而受到广泛关注, 而且可以通过改变其纳米粒子的形貌、表面元素分布和粒径大小而具有可调谐性能.采用分子动力学与蒙特罗方法并结合嵌入原子势对NiCu双金属纳米粒子的表面偏析、结构特征以及Cu吸附原子在Ni基底沉积生长与表面扩散进行了研究, 结果表明Cu原子在Ni基底表面具有强的偏析倾向.随着Cu原子浓度的增加,Cu原子优先占据纳米粒子的顶点、边、(100) 和 (111) 面, 最终形成完美的Ni核/Cu壳纳米粒子.在生长温度T = 400 K时, 形成的Ni核/Cu壳结构最稳定.进一步采用肘弹性波方法模拟计算在Ni基表面Cu吸附原子的扩散势垒, 结果表明, Cu吸附原子无论是交换还是扩散, 都需要克服较大的ES势垒, 从而难以在Ni基底表面进行面间扩散.与Ni基底相反, 在Cu基底上沉积Ni原子, Ni吸附原子很容易从 (111) 面迁移至 (100)面, 且在当前模拟温度下, Ni吸附原子无法在 (100) 面进行迁移, 导致生长构型朝正八面体的形状发展, 且其八个顶角几乎被Ni原子所占据.本文经过深入研究, 从原子的角度出发, 对NiCu纳米催化剂的初步设计提供了一种新的思路和方法.
1 引 言
与传统的宏观材料相比, 金属纳米粒子由于具有尺寸小、表面体积比高等优点, 其物理和化学性能有显著的提高[1].相对于单组分金属纳米粒子,双金属纳米合金因其优异的性能而被广泛研究.而金属合金的成分、结构和性能的丰富多样性使其在电子、工程和催化等领域得到广泛应用[2].在纳米尺度上制备具有明确可控性和结构特征的材料已成为国内外研究的热点, 根据应用需要调控其结构是纳米合金制备技术发展的方向.
采用分子动力学针对于双金属纳米团簇的研究主要有熔化[3]、烧结、生长扩散等, 如在熔化方面, 有Al-Pd[3], Au-Pt[4], Li-Fe[5], Pt-Pd[6,7]等; 在烧结模拟中, 有Ni-Al[8], Li-Pd[9], Au-Ag[10]等; 在生长扩散的模拟研究中, 有Co-Cu[11], Ni-Al[12,13],Mg-Al[12,14], Fe-Al[12,15], Ag-Cu[16,17], Ag-Pd[18], Ag-Ni[19]等; 基于蒙特卡罗方法, 在针对双金属纳米团簇的结构优化方面, 有Au-Pt[20], Au-Ag[21], Ag-Pt[22], Ag-Pd[23], Cu-Pt[24]等; 作为催化剂在催化领域的应用方面, 采用第一性原理方法研究涉及的双金属纳米团簇有Cu-Ni[25], Pt-Ni与Pt-Po[26], Au-Ag[27,28], Au-Ni[27]等.双金属NiCu纳米颗粒在甲烷分解、乙醇蒸汽重整、甲醇氧化和水-气转换等重要化学反应中被广泛用作催化剂, 由于NiCu核壳结构表现出铁磁性, 因此, NiCu纳米颗粒也被应用于磁性领域[29].NiCu双金属纳米合金的催化性能与其金属原子之间的浓度、原子间的分布和结构有很强的依赖关系.Bonet等[30]以碳酸镍和碳酸铜为悬浮液, 在具有溶剂和还原剂双重作用的乙二醇中用硝酸镍和硝酸铜溶液合成了双金属镍铜粒子, 而Chatterjee等[31]则采用多元醇还原法和物理熔融法制备了铜镍合金纳米粒子.同样, 在理论上也不乏关于NiCu金属纳米粒子的研究报道.Hristova等[32]使用基因遗传算法结合嵌入原子势(embedded atom method, EAM) 探究了原子数量N≤20以及N = 23和N = 28的整个浓度范围的NinCum(N = n + m) 双金属纳米粒子的最低能量结构.Xiao等[33]对FeCu, CoCu和NiCu纳米粒子作为合成气合成醇的催化剂做了对比研究,并发现NiCu纳米粒子可以作为甲醇催化剂.纳米颗粒形式的双金属催化剂因其选择性、高活性和稳定性等优点在许多领域得到了广泛的应用[34].
尽管之前有不少关于NiCu纳米粒子的研究报道[34−36], 然而, 关于NiCu纳米粒子的表面偏析、结构特征, 特别是尺寸、成份和温度的影响以及Cu吸附原子在Ni纳米粒子的表面扩散与生长的详细探究却未有报道.NiCu双金属纳米颗粒的性能很大程度上取决于合金的结构, 如混合合金、核壳合金或双面合金结构[35].然而, 从实验水平上探究NiCu纳米粒子的原子尺度结构和组成信息,仍然是一项非常复杂的工作.而第一性原理方法已经发展成为探索纳米团簇表面化学的有力方法[22,27,37], 而实际中的纳米催化剂通常由几百个原子组成, 这使得在双金属纳米团簇中, 精确的第一性原理方法需要大量的计算, 因而很难实际解决数万个原子组成的纳米团簇.作为一种选择, 分子动力学 (molecular dynamics, MD) 和蒙特卡罗(Monte Carlo, MC) 模拟结合EAM势成为研究双金属纳米团簇性质的有效工具, 能极大地简化问题的复杂度.因此, 这种方法为实验上设计NiCu金属纳米粒子催化剂提供了一个很好的见解, 为其他学者探究金属NiCu纳米粒子的电子性质和催化性能、设计NiCu纳米团簇的构型时提供了一个很好的思路.本文采用MC和MD方法并结合EAM势, 分别对截角八面体结构的NiCu双金属纳米粒子的表面偏析与结构特征和Cu吸附原子在Ni基底表面的扩散与生长进行了详细地研究.
2 模型与方法
金属纳米粒子通常呈现出正二十面体 (icosahedron, ICO)、截边十面体 (decahedron, DEC)、八面体(octahedron, OCT)、截半立方体 (cuboctahedron, CUB) 和截角八面体 (truncated octahedron, TOC)等几何形貌.对于面心立方晶体 (face center cubic, FCC), 从中截取的典型团簇为OCT结构, 它是由两个正四棱锥对接而成.虽然OCT的表面原子均为密排结构, 但其表面形状与球形相差甚远, 形成团簇的表面能不是最低的, 而且面/体原子数之比较大, 从而导致团簇的能量没能达到势能的局部最小.为了使OCT的表面与球形接近,进行轻度截切, 即从OCT的6个顶角各截去四层原子, 留下6个5 × 5的正方形截面, OCT的8个原表面则变成了六边形, 即可得到原子数N =1289的TOC结构(图1 (a)插图).较低表面体积比的TOC形态被认为是FCC晶体金属纳米粒子的特有结构[38−40].一个典型的TOC纳米粒子, 共包含6个 (100) 面, 8个 (111) 面, 12个 (111)/(111)边, 24个 (100)/(111) 边和24个顶点, 被认为是最有利的几何构型.考虑到计算成本, 本研究小组主要研究了原子数N (N = 586, 1289, 2406和4033)为“幻数”的TOC纳米粒子, 它们的原子壳层是完整的.若用 m 代表纳米粒子表面台阶边缘上的原子数, 则TOC纳米粒子的总原子数 NTOC为[41]
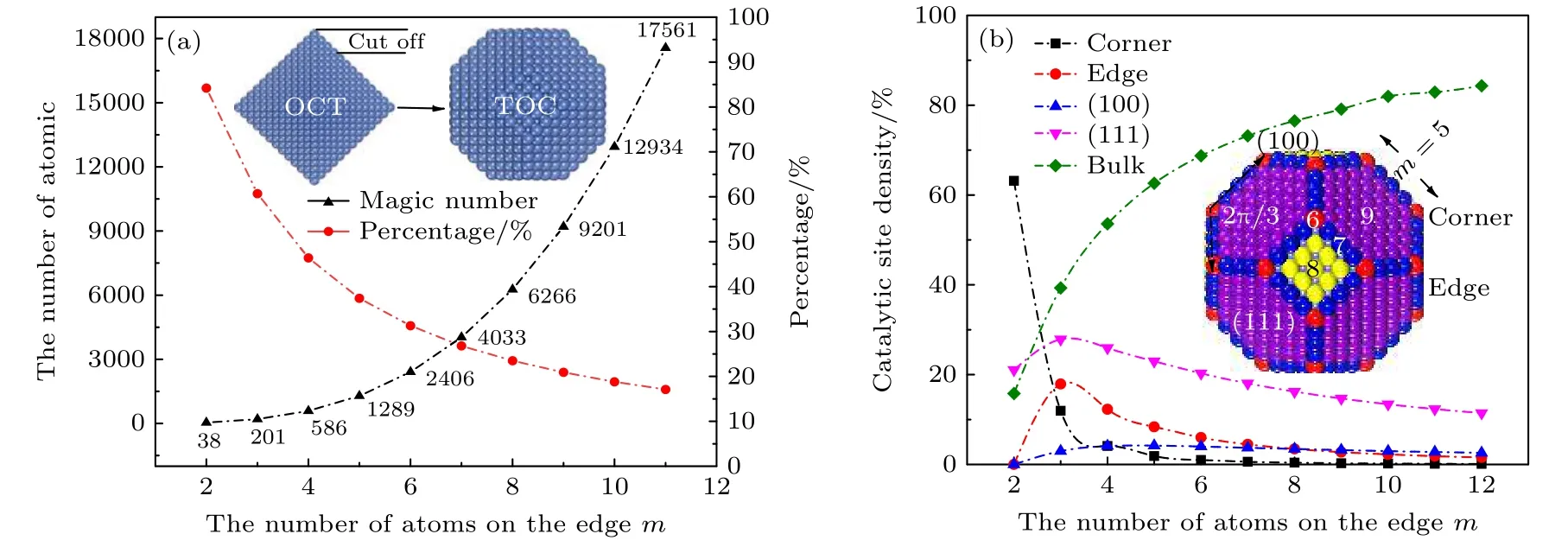
图1 (a) TOC结构纳米粒子的总原子数与表面原子数比例随尺寸的关系; (b) TOC纳米粒子的表面催化位点比例随尺寸的关系Fig.1.(a) The total atom number and surface atom percentage of TOC structure nanoparticles as a function of nanoparticle size;(b) the relationship between the surface catalytic sites density of TOC structure nanoparticles and the size of nanoparticles.
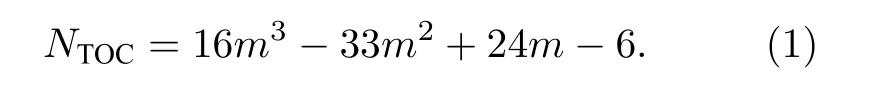
采用MC和MD模拟方法对原子数量范围从586到4033的TOC形貌的Ni1–xCux(x = 0.125,0.250, 0.375, 0.500, 0.625, 0.750和0.875) 双金属纳米粒子的表面偏析、结构特征进行研究.为了进一步考虑温度的影响, 所选取温度T分别为200,400, 600, 800和1000 K.在表面偏析与结构特征的研究中, 初始的TOC形貌的Ni1–xCux纳米粒子是将纯Ni纳米粒子中的一部分Ni原子, 根据所需浓度随机替换成Cu原子, 然后利用Lammps中基于Metropolis算法的fix atom/swap命令随机选取Ni, Cu两个原子进行尝试交换.由于该命令只能进行两种原子位置的交换而不能进行位置弛豫,因此每次交换完毕后, 都要在正则系综 (canonical ensemble, NVT) 下对整个纳米粒子进行等温弛豫, 所有的纳米粒子均进行了10000次MC + MD步以确保达到平衡, 在每一步骤下尝试交换的次数为对应纳米粒子的总原子数.在系统达到平衡状态后, 通过平均超过1000次MC + MD步骤计算得到所需的量, 如化学物质的浓度分布等.
为了实现纳米合金的动态生长, 采用MD方法对Cu吸附原子在Ni基底的表面沉积生长与扩散进行研究.在生长过程中, 原子的注入方式是将Cu原子从半径R = 35—36 Å的球壳区域, 一个一个朝着Ni基底质心随机沉积到Ni基衬底的表面,沉积Cu原子的能量为0.1 eV/atom, 该方法可通过Lammps中的fix deposit命令实现.为了保证沉积原子的充分扩散, 注入原子的速率为1 ns/atom,所选取的系综是NVT系综.系统的运动方程遵循牛顿定律, 原子运动的数值积分算法采用的是具有时间反演对称的Verlet算法, 时间步长 ∆t = 2 fs.在扩散过程中, 向原子添加推动力时通过肘推弹性波 (nudged elastic band, NEB) 方法找到过渡态,并计算扩散能垒.在整个模拟的过程中采用的EAM势是由Onat和Durukanoglu[42]开发的, 该势函数通过拟合Cu, Ni和Cu-Ni二元化合物的实验和第一性原理数据, 如晶格常数、内聚能、体模量、弹性常数、双原子键长和键能等进行确定, 因此该势能函数能够很好地描述Ni, Cu金属之间的相互作用.所有的模拟仿真软件采用Lammps[43]程序包, 并使用Ovito[44]分析软件对数据结果进行数据分析.
3 结果与讨论
3.1 Ni, Cu纳米粒子的熔化
长期以来, 纳米材料的熔化都是理论和实验研究的主要课题[45,46].为研究原子数N = 586—4033具有TOC形貌的Ni, Cu纳米粒子的熔点, 在0—2000 K的加热过程中, 纳米粒子的温度增量每步为50 K.考虑到熔点附近的温度波动, 温度增量减小为10 K[47].图2所示为Ni, Cu纳米粒子每原子的平均势能和林德曼指数随温度的变化关系.其中, 基于原子间距波动的Lindeman 指数能够定量地描述一个系统的熔化机制, 又由于在Lindeman指数中包含了均方根的概念, 因此它能够描述每原子的一个流动状态, 指数越高, 说明该原子运动越无序, 流动性越强.对于一个具有N个原子的系统, 系统中每原子的Lindeman 指数定义为均方根键长波动, 其表达式为[4]
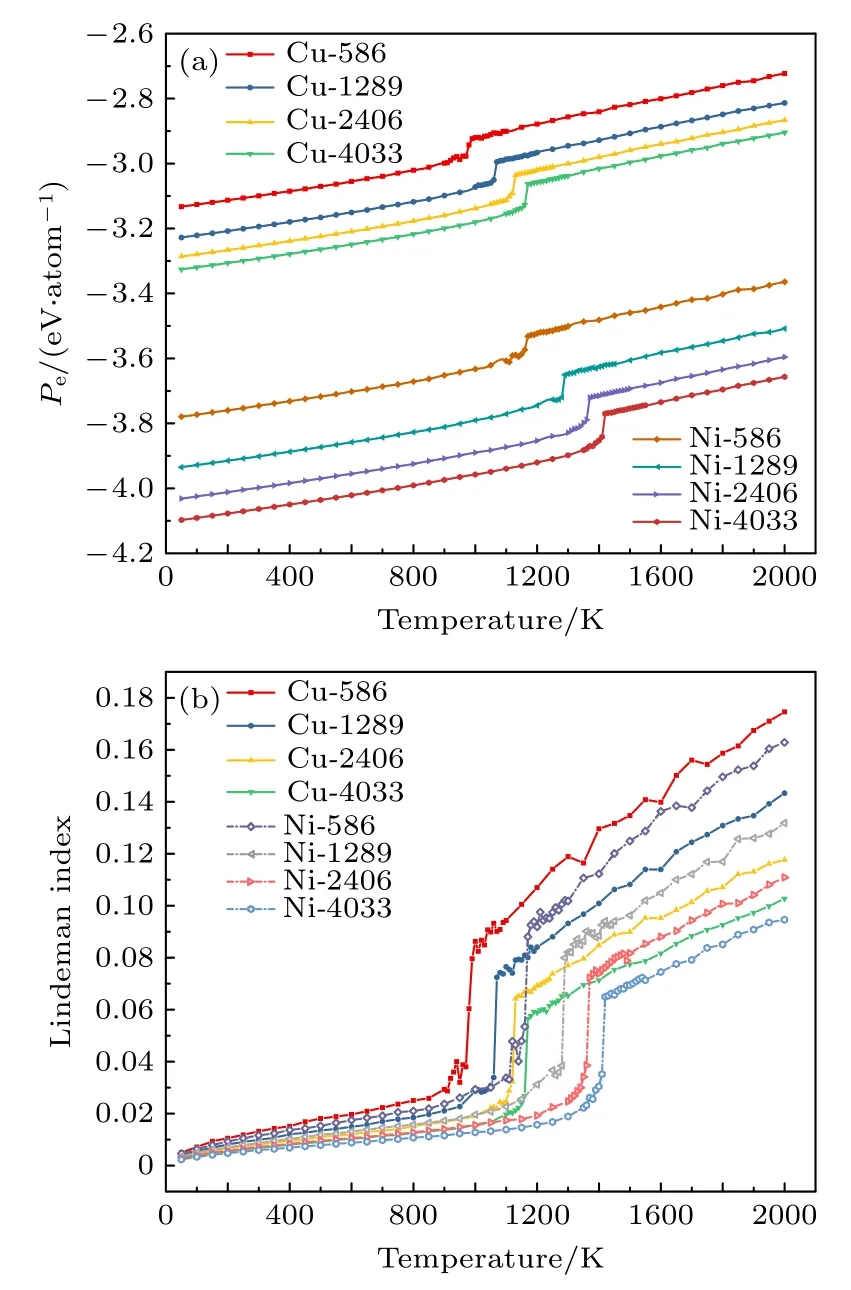
图2 具有TOC结构的Ni和Cu纳米粒子的每原子势能和林德曼指数随温度的变化Fig.2.Relations of the potential energy per atom and Lindemann index as a function of temperature for the Ni and Cu nanoparticles with TOC structures.
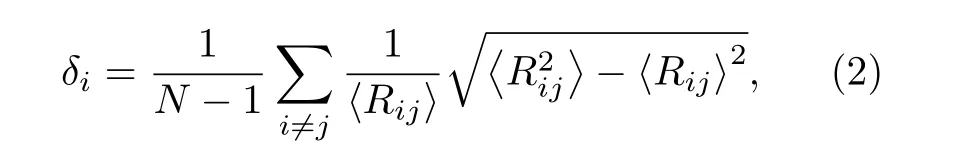
其中Rij是第i个和第j个原子之间的距离.系统的平均Lindeman 指数由下述方程给出
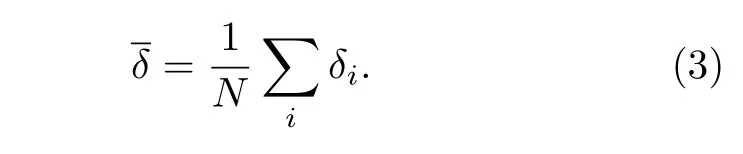
Lindeman判据表明, 当原子热振动的均方根振幅达到最近邻分离的临界分数时, 即发生熔化, 从而使相邻原子之间发生直接碰撞[4].
如图2(a)所示, 在低温下, 每原子的势能几乎随温度线性增加, 熔点位于观察到热曲线急剧跃升的位置, 能量的变化是由于熔化的潜热引起的[5].从势能曲线上可以清楚地看出加热温度对纳米颗粒大小的依赖性.纳米颗粒的熔点随着纳米粒子的尺寸增加而增加, 最终趋向于块体熔点[48−51].在相同尺寸下, Ni纳米粒子的熔点高于Cu纳米粒子,这一现象与在实验上块体Ni的熔点 (1728 K) 显著地高于块体Cu的熔点 (1357 K)[42]一致.当这些纳米颗粒完全熔化时, 就会出现急剧的跳跃.如图2(b)所示, 势能和林德曼指数的跳跃同时发生.根据计算获得的纳米粒子熔点, 选择在温度T =200—1000 K下, 对NiCu纳米粒子的表面偏析和结构特征进行研究, 在该温度下纳米粒子处于固态.
3.2 NiCu纳米合金的表面偏析与结构特征
图3所示为200 K下原子数为586的NiCu双金属纳米粒子中Cu的分布随Cu浓度的变化.从图3可以看出, 随着Cu原子浓度的增加, 不仅Cu原子整体的表面呈现偏析行为, 而且Cu原子在纳米粒子的表面也展现出多位点的偏析竞争.其中Cu原子的占位依次是顶点、边、(100) 面和(111) 面, 然后是体内.利用密度泛函理论 (density functional theory, DFT) 方法, Wang等[52]最近对13原子和55原子的Cu和Cu-Ni核壳纳米粒子的结构、稳定性、电荷转移、电子和磁性进行研究, 发现Ni核/Cu壳比Cu核/Ni壳纳米粒子拥有更低的能量优势.Quaino等[34]采用晶格蒙特卡洛和分子动力学模拟方法对CUB形貌的NiCu纳米粒子进行研究, 发现Cu原子展现出很强的表面偏析.一般而言, 表面能小的金属原子倾向于占据纳米粒子的表面, 有利于系统能量的降低确保稳定结构形成, 偏析的NiCu纳米合金的原子构型是由表面能、晶格畸变和结合能之间的平衡决定的[20].
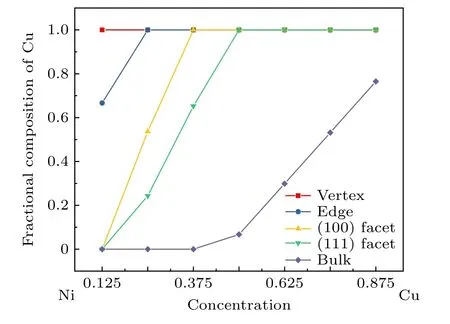
图3 在200 K, 586原子的Ni1–xCux双金属纳米粒子中Cu的分布随Cu浓度的变化Fig.3.Variation of the fractional composition of Cu at different surface sites as a function of overall Cu composition for 586 atom nanoparticles at T = 200 K.
表面能 (Esurf) 定义为一个特定的晶体平面单位面积上的表面多余自由能, 它决定了晶体的平衡形态, 对晶体的形成、粗化和生长起着重要的作用,其计算的表达式如下[53,54]:
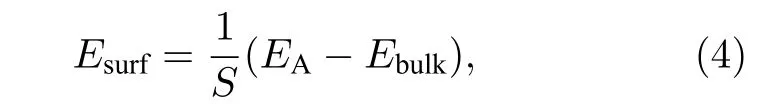
其中EA是系统为自由表面时的总能量, S是体系自由表面的表面积, Ebulk表示在周期性条件下系统的总能量.TOC形貌的纯Ni, Cu纳米粒子的表面能随尺寸的关系如图4所示, 随着纳米粒子尺寸的增加, 其表面能逐渐减少并趋向一个极限值,主要是由于小尺寸的纳米粒子具有更高比例的表面原子.从图4可以看出, 在相同尺寸下, Cu纳米粒子比Ni纳米粒子拥有更低的表面能.此外,相比金属Cu, 金属Ni具有更低的内聚能, 二者的内聚能分别为–3.54和–4.45 eV/atom[42].因此,Cu纳米粒子相对Ni纳米粒子更趋向于纳米粒子表面.
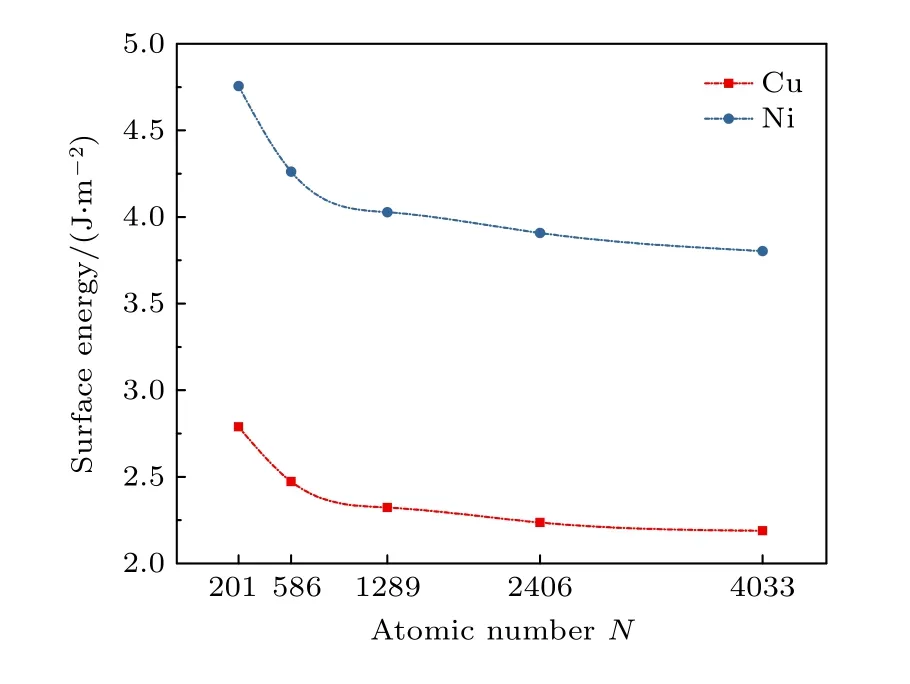
图4 Ni, Cu纳米粒子的表面能随原子尺寸的关系Fig.4.Variation of the surface energy of Ni and Cu nanoparticles as atomic number.
偏析 (通过目前的MC + MD模拟获得) 和随机 (无序固溶体) 的Ni1–xCux纳米粒子形成热结果如图5所示, 为了减少误差, 通过1000个构型对形成热结果进行统计平均, 纳米粒子每个原子的平均形成热 ( ∆H)[55]计算如下式:
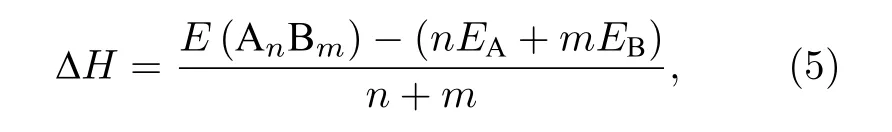
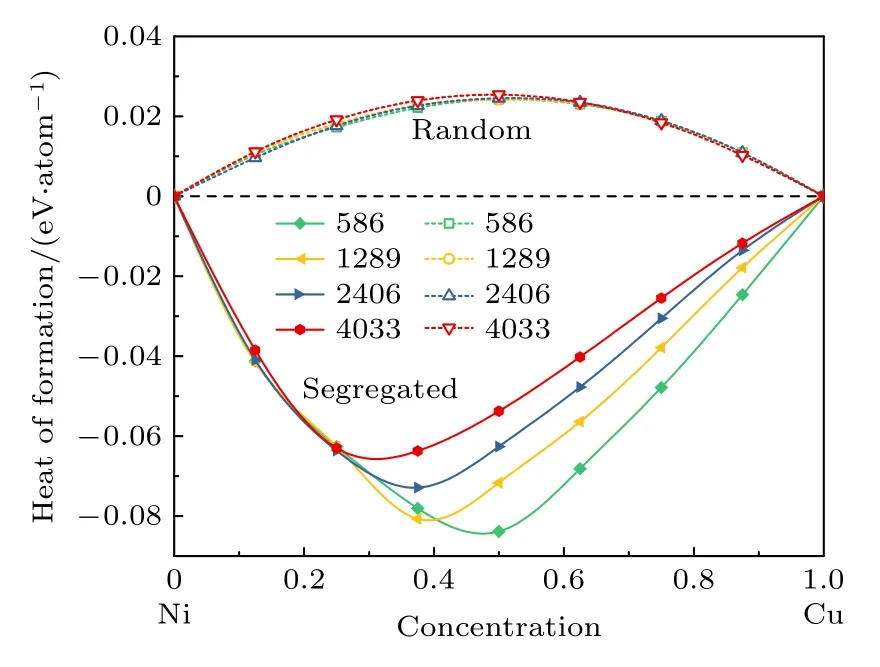
图5 随机和偏析结构的Ni1–xCux双金属纳米粒子的形成热与Cu原子浓度的变化关系.实线为偏析结构, 虚线为随机结构Fig.5.The formation energy of Ni1–xCux bimetallic nanoparticles with random and segregation structure varies with the concentration of Cu atom.The solid line is a segregation structure, and the dotted line is a random structure.
其中n和m分别表示A类原子和B类原子的数量, E (AnBm) 表示化合物 AnBm的总能量, EA和EB分别为金属A和B的每原子的能量.从图5可以看出, 由于Ni和Cu原子的随机混合和尺寸效应, 随机纳米粒子的形成热为一较低的正值.然而,对于偏析的纳米粒子来说, 由于Cu原子的表面偏析, 其最显著的特征之一是形成热为负值, 这意味着偏析的Ni1–xCux纳米粒子比随机Ni1–xCux纳米粒子更具热力学稳定性.因此, 从热力学角度分析,Ni核/Cu壳结构更为稳定.
对于Ni1–xCux纳米合金中Cu原子的表面位点的偏析竞争现象进一步通过构型能差( ∆ E ) 进行理解, ∆ E 被定义为内部Cu原子与表面Ni原子交换后的能量差值, 计算公式[20,56]如下:
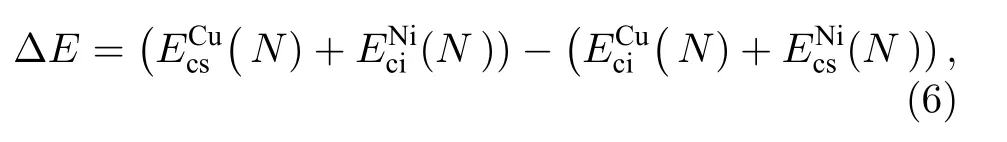
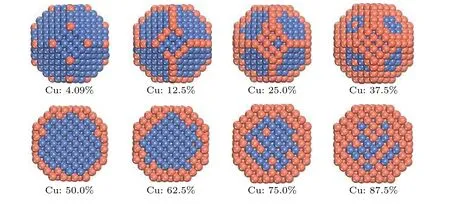
图6 在200 K, 586个原子TOC形貌的Ni1–xCux双金属纳米粒子结构.橘红色和海蓝色的球分别表示Cu原子和Ni原子Fig.6.Configurations and cross-section snapshots of 586 atom TOC Ni1–xCux nanoparticles at T = 200 K.The orange-red and seablue balls represent Cu atoms and Ni atoms, respectively.

表1 对于586原子的TOC纳米粒子, 内部Cu原子与表面Ni原子交换后构型能差值 (∆E, 单位: eV/atom),数字6, 7, 8, 9和12分别表示顶点、边缘、(100) 面、(111) 面和体内的位置Table 1.Configuration energy difference values (∆E,unit: eV/ atom) for a bulk Cu atom exchanging with surface Ni atoms for the TOC nanoparticles of 586 atoms.The numbers 6, 7, 8, 9, and 12 are represent the sites at the vertex, edge, (100) facet, (111) facet, and bulk, respectively.
3.3 生长与扩散
以1289原子TOC形貌的Ni核为基底, 通过随机沉积Cu原子至Ni核表面来实现动态的生长模拟, 当沉积的Cu原子数等于800时, 停止沉积.利用纳米颗粒表面原子数 ()和内部原子数定量描述了双金属纳米颗粒结构的生长, 其中A和B分别表示基底原子和注入原子,的交叉点定义为核壳团簇的缺陷数(Ndef), 根据Baletto的描述, Ndef越小, 形成的核壳结构越好[19].在温度T = 200—800 K时,和沉积Cu原子数 (Ndep)如图7所示.在沉积的开始, 随着Ndep的增加,几乎是线性减少,则几乎是一个接近于0的小值.结果表明, 入射的Cu原子占据表面位点, 没有进入Ni基衬底的内部.随着Ndep持续增加,开始缓慢增加, 最终与交叉.主要原因是后沉积的Cu原子覆盖了已有的Cu壳原子, 形成第二层; 或一部分Cu原子与Ni基底台阶边缘的原子交换,进入Ni核内部成为体原子[11,12,57].从图7可以看出, Ndef处于较低的水平, 说明在整个温度范围内都能形成较好的Ni核/Cu壳结构.这与之前MC+ MD的结果一致, Ni核/Cu壳的纳米粒子更稳定.当生长温度为400 K时, 对应的交叉点Ndef处于最低水平, 说明温度400 K最利于Ni核/Cu壳结构的形成.

图7 在温度T = 200, 400, 600和800 K下, 与沉积的Cu原子数的函数关系Fig.7.The growth of Cu atoms on the TOC Ni substrate with 1289 atoms at T = 200, 400, 600, and 800 K, theand as a function of the deposited Cu atoms (Ndep).
为了更加清晰地阐明Ni核/Cu壳的动态生长过程, 给出了T = 400 K时Cu原子在TOC结构的Ni基底表面的生长序列(图8).从图8(a)—(f)可以看出, 沉积的Cu原子数分别为100, 200,300, 400, 500和600.随着Ndep的增加, Cu原子逐渐覆盖Ni核基底, 当Ndep= 600时, 形成相对完整的核壳结构.类似的还有Al-Mg, Cu-Co和Ni-Ag等[11,12,19]核壳结构.在生长过程中, 基底台阶边缘上少量Ni原子被沉积的Cu原子所取代.采用NEB方法系统地研究了Cu吸附原子在镍基表面的 (111) 面到 (100) 面和 (111) 面到 (111)面之间的扩散势垒, 结果如图9(a)和图9(b)所示.
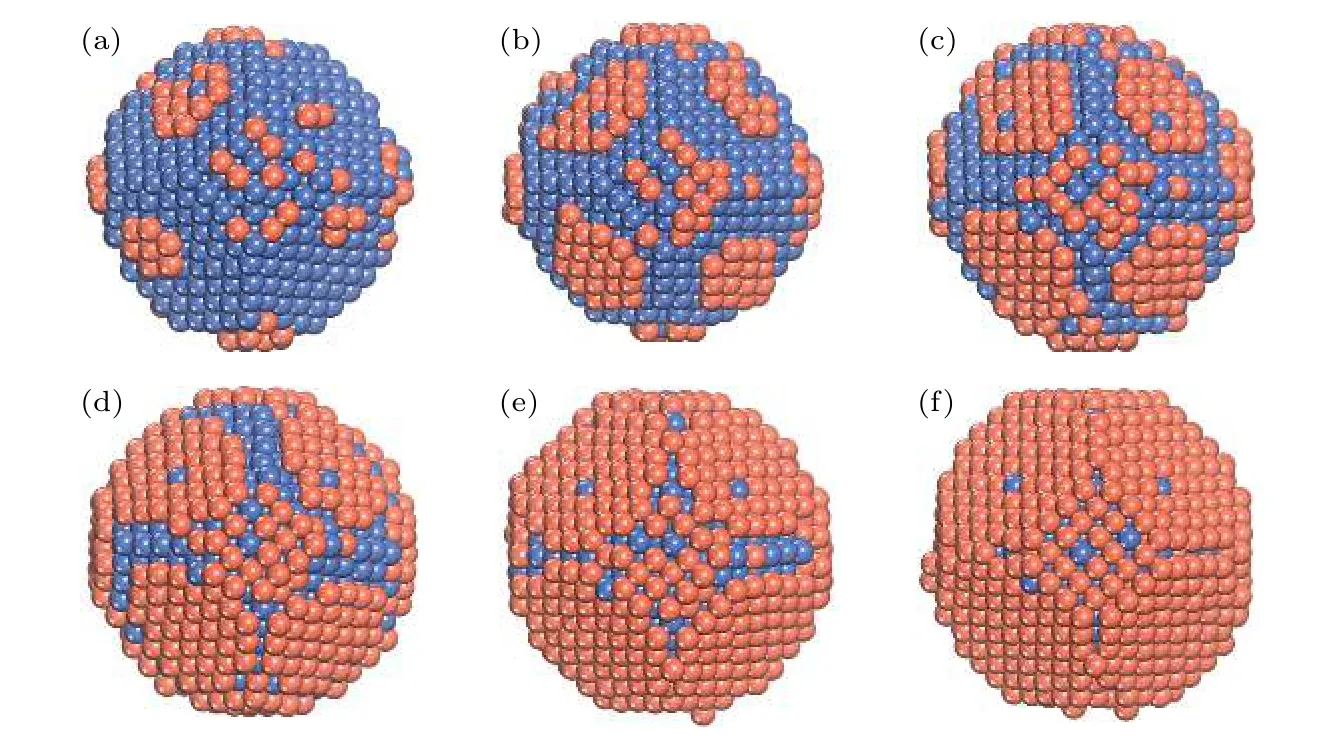
图8 T = 400 K, Al原 子在Ni TOC1289基底 上 的 生长序列 (a) Ndep = 100; (b) Ndep = 200; (c) Ndep = 300; (d) Ndep = 400;(e) Ndep = 500; (f) Ndep = 600.橘红色和海蓝色的球分别表示Cu原子和Ni原子Fig.8.Growth sequence of NiCu clusters at T = 400 K.The snapshots of the growth simulation for various Ndep of 100, 200, 300,400, 500, and 600.The orange-red and sea-blue ball show the Cu and the Ni atom, respectively.
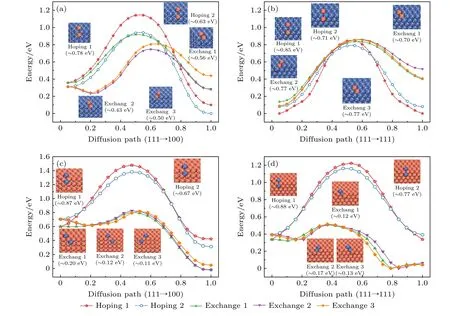
图9 Cu (Ni) 吸附原子在Ni TOC1289 (Cu TOC1289) 基底表面的扩散势垒 (a) Ni-基底 (111)→(100); (b) Ni基底 (111)→(111);(c) Cu基底 (111)→(100); (d) Cu基底 (111)→(111).橘红色和海蓝色的球分别表示Cu原子和Ni原子Fig.9.The diffusion energy barrier of Cu adatom on the surface of the Ni TOC1289: (a) Ni-base (111)→(100) facet; (b) Ni-base(111)→(111) facet; (c) Cu-base (111)→(100) facet; (d) Cu-base (111)→(111) facet.The orange-red and sea-blue balls represent Cu atoms and Ni atoms, respectively.
金属原子的扩散机制主要分为两类: 一类是跳跃机制 (hoping), 即吸附原子从一个平衡位置跨过能量势垒进入另外一个新的平衡位置进行扩散; 另一类是交换机制 (exchange), 当吸附原子到达台阶边缘, 它会推出台阶边缘原子然后占据其留下的空位, 随后边界原子成为新的吸附原子在邻面上进行扩散[58].对比在平面上的扩散, 其中一个额外的势垒在台阶的边缘存在, 即Ehrlich-Schwoebel (ES)势垒[59,60].
如图9(a)和图9(b)中插图所示, Cu吸附原子从Ni基表面的 (111) 面扩散至邻近的 (100) 面或 (111) 面, 有两种不等价的跳跃路径和三种不等价的交换路径, 为了便于区分, 其跳跃路径分别标注为Hoping 1和Hoping 2, 交换路径分别标注为Exchange 1, Exchange 2和Exchange 3.反应坐标由初始构型和最终构型之间的距离进行归一化,0和1.0分别对应扩散路径的初始构型和最终构型, 取扩散路径中系统的最小能量为零.对于吸附原子在 (111)→(100) 面之间的扩散, 其Exchange机制占优势, 最低的ES势垒约为0.43 eV, 对应的扩散路径为Exchange 2.然而, 对于吸附原子在(111)→(111) 面之间的扩散, 有两个几乎相等较低的ES势垒, 分别为Hoping机制 (约为0.71 eV)和Exchange机制 (约为0.70 eV), 对应的扩散路径分别为Hoping 2和Exchange 1.因此, Cu吸附原子在Ni TOC1289表面进行面间扩散的最有利机制为 (111)→(100) 面之间的Exchange机制.由于Cu吸附原子无论是交换还是跳跃, 都具有较高的扩散能垒, 这使得在温度T = 400 K下难以在Ni基底表面进行面间扩散进而形成较为完美的Ni核/Cu壳纳米粒子.
在400 K时往Cu TOC1289上沉积Ni原子,其生长序列如图10所示.Ni原子优先倾向于扩散至Cu基底的 (100) 面, 并随着沉积Ni原子数量的增加, 纳米粒子构型逐渐形成正八面体结构.从扩散的角度分析, 这种情况出现的主要原因是Ni吸附原子在Cu基底表面很容易从 (111) 面向(100) 面发生扩散, 在目前的模拟温度下, Ni原子无法在 (100) 面上迁移, 其扩散能垒如图9(c), (d)所示.
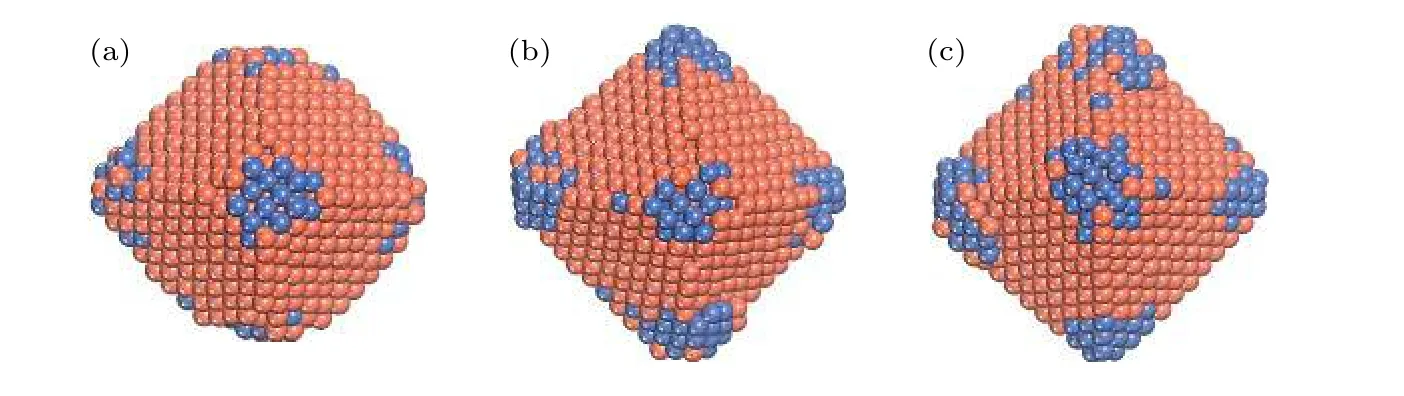
图10 T = 400 K, Ni原子在Cu TOC1289基底上的生长序列 (a) Ndep = 100; (b) Ndep = 200; (c) Ndep = 300.橘红色和海蓝色的球分别表示Cu原子和Ni原子Fig.10.Growth sequence of NiCu clusters at T = 400 K: (a) Ndep = 100; (b) Ndep = 200; (c) Ndep = 300.The orange-red and seablue ball show the Cu and the Ni atom respectively.
4 结 论
采用MC与MD方法并结合EAM势系统地研究了原子数从586至4033的TOC形貌的NiCu纳米粒子的熔化、表面偏析、结构特征, 进一步采用NEB与MD方法对单个的Cu吸附原子在Ni衬底表面的扩散和沉积生长进行了研究.在相同尺寸下, Cu纳米粒子的熔点显著低于Ni纳米粒子的熔点, 随着颗粒尺寸的增大, 纳米粒子的熔点也随之增大.
在相同尺寸、温度和浓度下, NiCu纳米合金中Cu原子均表现出较强的表面偏析倾向.在NiCu纳米粒子的表面, Cu原子存在多位点的表面偏析趋势.由于Cu原子与表面不同配位数的Ni原子交换后构型能差值不同, Cu原子依次优先倾向占据位于顶点、边、(110) 面和 (111) 面的位置, 当Cu原子的浓度达到50%时形成完整的TOC形貌的Ni核/Cu壳纳米粒子.
在温度T = 200—800 K时, 对Cu吸附原子在Ni TOC1289表面的沉积生长进行研究, 发现Cu吸附原子无论是交换还是跳跃, 在Ni基底表面扩散的能垒都较高, 使得Cu吸附原子难以发生面间扩散.在当前模拟温度范围内能形成较好的Ni核/Cu壳结构, 且当生长的温度为400 K时, 最利于Ni核/Cu壳结构的形成.相反, 在Cu基底上沉积Ni原子时, Ni吸附原子很容易从 (111) 面迁移至 (100) 面, 在当前模拟温度下, Ni吸附原子无法在 (100) 面进行迁移, 导致纳米粒子的构型朝正八面体的形状发展, 且其八个顶角几乎被Ni原子所占据.

