基于学习矢量量化的空调压缩机声纹诊断方法
欧阳城添,袁 瑾
(江西理工大学 信息工程学院,江西 赣州 341000)
0 引 言
空调压缩机是空调的重要部件,一旦压缩机发生故障,空调将失去制冷功能。因此,在出厂之前对压缩机进行严格的质量检测是避免故障压缩机流向市场的重要手段。针对压缩机的故障诊断,国外有Smith等[1]利用参数选择和数据压缩技术减少了压缩振动信号分析的计算量,并提高了故障分类效果;Alekseev等的文章[2]介绍了常用的压缩机振动信号分析算法并设计了一套振动信号的接收、处理和存储的软件。在国内,张明等[3]依靠多种类型的传感器采集压缩机振动信息,提出了一种基于多源信息融合的故障诊断方法对压缩机的3种工况进行融合诊断。在信号分析方面,PCA分析[4,5]、傅里叶变换[6,7]、小波分析[8,9]等也在压缩机故障诊断中得到应用。虽然上述方法在压缩机故障诊断中取得了不错的效果,但是传统技术多采用振动传感器采集压缩机工况信号,这种“接触式”采集方式部署困难,不利于生产厂商进行高效的大规模检测。针对这一缺点,本文提出一种基于学习矢量量化(learning vector quantization,LVQ)神经网络的故障压缩机声纹识别(voiceprint recognition)模型用于空调压缩机故障诊断。本文采用“非接触”的形式采集压缩机工作噪音进行诊断,克服了传统方法信号采集效率低下缺点。同时,用于建模的LVQ神经网络具有构造简单、不依赖大数据集、分类简单等优点。
1 压缩机声纹识别模型描述
声纹识别,又被称之为说话人识别(speaker recognition),该技术通过对人的声音信号的特征向量进行分析,以达到区分说话人的目的[10-13]。本文基于以下两点原因,试图使用声纹识别技术进行故障压缩机的识别。首先,工作中的压缩机会产生工作噪音,其中蕴含着压缩机工作状态的信息,因此将声纹识别技术应用于压缩机故障诊断具有一定的可行性;其次,与以往使用传感器采集振动数据不同,声音信号使用的是“非接触式”采集方式,采集信号的麦克风不需要接触压缩机,因此声纹识别技术具有更简单的操作性。目前,已有学者利用声纹识别技术对变压器进行了故障诊断,取得了非常理想的效果[14]。
LVQ神经网络又称为LVQ分类器(LVQ classification[15]),是一种前馈神经网络,属于有监督学习,LVQ神经网络的学习算法被称为LVQ算法(LVQ algorithms)。LVQ神经网络具有设计简单,分类效果好,收敛速度快等特点,被广泛应用于模式识别领域[16,17]。
1.1 声纹识别技术流程
声纹识别技术的应用可以分为模型建立和模型应用两个阶段,如图1所示。

图1 声纹识别技术流程
关键的模型建立阶段可以分解为3个步骤:
(1)收集声音数据;
(2)提取声音信号特征;
(3)建立分类模型。
其中,提取声音信号特征是关键步骤。根据新西兰学者Tirumala等[18]的综述统计,在现有的声音信号特征提取方法中,梅尔倒谱系数(Mel frequency cestrum coefficient,MFCC)应用最为广泛。本文也将使用MFCC作为压缩机声纹识别模型的特征提取方法。
1.2 声音信号处理
在声纹识别技术中,由于人类发声器官特性和声音信号采集设备等原因,会造成信号混叠、谐波失真等干扰,加之人类声音具有短时稳定性,因此在特征提取之前必须对声音信号进行预处理[19]。采集后的压缩机的噪声信号同样具有以上缺陷,因此也需要进行相应的预处理。但由于机械声音与人类声音存在一定差异,因此本文采用的预处理方法与通常采用的人类声音预处理方法有所不同,具体会在下文中提到。
声音信号预处理主要包括预加重、分帧、加窗等操作。对声音信号采集后,首先进行预加重处理,其目的是对声音信号的高频部分进行加重,弥补高频分量的损失。预加重的滤波器常设为
H(z)=1-az-1
(1)
随后,将一段长的声音数据划分为若干个小片段,称为分帧。声音信号分为较短的帧,可以将每帧的声音信号看成一个稳态信号,为了保证相邻帧之间的参数能够平稳过渡,两帧之间应有部分重叠,可表示为
F=n-wo/[w(1-o)]
(2)
式中:其中F为分帧数,w为帧长,o为重叠率,即帧移占帧长百分比。在声纹识别技术中,由于人声的短时平稳性,一般取20 ms到30 ms为一帧,以使得特征参数平稳变化。压缩机噪声相较于人声而言,具有更大的平稳性,因此本文根据文献[14]在变压器中的分帧方法,取帧长为500 ms,重叠率为40%。
预处理后的声音信号在提取特征时需要进行傅里叶变换,为了减少信号在频域中的泄露,将对每帧声音信号施加汉明窗(Hamming)。汉明窗公式为
(3)
式中:L为汉明窗长。
1.3 MFCC特征向量的提取
MFCC系数是基于人耳听觉实验得到的一种声音特征向量,是应用最广的声音特征,已有不少学者对MFCC进行了优化[20,21]。MFCC是一种基于Mel频域的系数,Mel频域表示的是基于人耳的非线性特征频率。Mel频率与声音信号频率的关系可以表示为公式
(4)
式中:Mel(f)为梅尔频率,f为声音普通频率,单位为赫兹(Hz)。作为声纹识别模型的关键步骤,本文有必要详细介绍MFCC特征向量的提取方法:
(1)离散傅里叶变换
对于每帧声音信号进行离散傅里叶变换的频域数据,公式为
(5)
式中:N为每帧的样本数量。
(2)计算能量频谱
谱线能量是频域数据的平方,公式为
Pm=|X(k)|2
(6)
(3)Mel三角滤波
Mel滤波由若干个三角带通滤波器Hm(k)组成,在Mel频域内,这些滤波器是等带宽的,这些滤波器可以表示为
------------------
(7)
------------------

(4)计算对数频谱
为了得到的结果对噪音干扰具有更强的鲁棒性,通过对能量频谱计算对数频谱
(8)
式中:Hm(k)是滤波器,S(m)是对数频谱,Pm是能量频谱。
(5)离散余弦变换
通过对上述计算得到的数据进行离散余弦变化即可得到MFCC特征向量,公式为
(9)
式中:C(n)为每帧声音信号的MFCC特征向量。
1.4 LVQ神经网络
LVQ神经网络是一种前馈神经网络,与常见的机器学习算法K-Means类似,也是通过寻找一组原型向量来构建聚类结构,但与K-Means不同的是,LVQ神经网络需要样本带有类别标记,学习过程采用了有监督的学习方法。
LVQ神经网络由输入层、竞争层和线性输出层组成。输入层与竞争层之间为全连接,竞争层与线性输出层之间为部分链接。LVQ神经网路具体结构如图2所示,LVQ神经网络模型如图3所示。
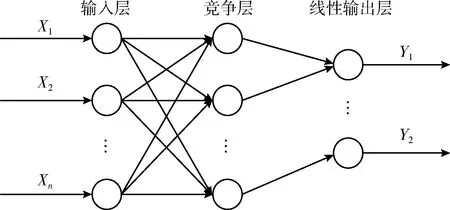
图2 LVQ神经网络结构

图3 LVQ神经网络模型
图3中,R为输入层神经元个数;S1与W1分别为竞争层神经元个数和权重矩阵;S2和W2分别为线性输出层神经元个数和权重矩阵。
最初的LVQ1算法(LVQ1 algorithm)存在着许多弊端,例如收敛性能不佳,靠近决策边界的样本分类效果不好,对重叠数据敏感等[22]。针对上述问题,提出了改进的LVQ算法(LVQ2,LVQ3),具体演变过程将在下文详细介绍。
(1)LVQ1算法
LVQ1算法的基本思想是:随机初始化权重矩阵,每一轮迭代中,随机选取一个训练样本,计算与样本距离最近的竞争层神经元,该神经元成为“获胜神经元”,根据比较与“获胜神经元”连接的线性输出层的神经元的标签与样本标签是否一致来更新竞争层神经元权重。如果标签一致,则更新对应的竞争层神经元的权重,使其向输入样本方向移动。否则,更新对应的竞争层神经元权重,使其向输入样本的反方向移动。LVQ1算法的详细过程如算法1所示。
算法1:LVQ1算法
输入:样本集D={(x1,y1),(x2,y2),…,(xm,ym)};竞争层神经元个数q;学习率α
输出:更新权重W
(1)对权重矩阵W进行随机初始化,为学习率α初始化赋值。
(2)将输入特征向量X=(x1,x2,…,xm)输入到输入层,抽取第i个训练样本xi,计算第j个神经元与样本xi之间的欧几里得距离
(10)
(3)找出一个竞争层神经元j,其到样本xi距离最小,记其输出的类型标记为cj。
(4)如果cj=yi,那么将对应输入层与竞争层之间权重做如下更新
wij=wij+α(xi-wij)
(11)
否则,权重做如下更新
wij=wij-α(xi-wij)
(12)
(5)一种重复(2)至(4)直到满足设定的迭代次数T或者设定的误差精度e位为止。
原始的LVQ1算法有以下缺点,首先,算法单次迭代只更新单个获胜神经元的权重,如果某些神经元在竞争中一直失败,就形成了“死神经元”,永远不会更新;其次,该算法使得竞争层神经元远离了决策边界,因此,靠近决策边界的样本分类正确率不高。最后,该算法对于重叠的数据集异常敏感。
(2)LVQ2算法
针对LVQ1算法的缺点,出现了改进的LVQ2算法,该算法每次迭代更新两个竞争层神经元,目的是对理论贝叶斯决策边界进行差分估计。LVQ2引入了“次获胜”神经元,在每次迭代中“获胜神经元”与“次获胜神经元”的权重都将得到更新。LVQ2算法引入了一个“窗口”参数,窗口的参数为σ,在每一轮迭代中,LVQ2算法会试图更新两个权重向量,其中一个是输出层与样本标签一致的竞争层神经元权重,一个是标签不一致的竞争层神经元权重。窗口的表示如下
(13)

算法2:LVQ2算法
输入:样本集D={(x1,y1),(x2,y2),…,(xm,ym)};竞争层神经元个数q;学习率α
输出:更新权重W
(1)对权重矩阵W进行随机初始化,为学习率α初始化赋值。
(2)将输入特征向量X=(x1,x2,…,xm)输入到输入层,抽取第i个训练样本xi,计算第j个神经元与样本xi之间的欧几里得距离
(14)
(3)找出两个竞争层神经元j、k,到样本xi距离最小,记其输出的类型标记为cj,记其输出的类型标记为cj,ck。

(5)如果cj=yi,则权重更新如下
(15)
否则,如果ck=yi,则权重更新如下
(16)
(6)如果dj≤dk,则执行(7),否则执行(8)。
(7)如果cj=yi,则权重更新如下
wij=wij+α(xi-wij)
(17)
否则
wij=wij-α(xi-wij)
(18)
(8)如果ck=yi,则权重更新如下
wik=wik+α(xi-wik)
(19)
否则
wik=wik-α(xi-wik)
(20)
(9)一种重复(2)至(8)直到满足设定的迭代次数T或者设定的误差精度e位为止。
LVQ2算法虽然对LVQ1算法进行了改进,但是LVQ2存在着收敛性能不佳的缺点。
(3)LVQ3算法
LVQ3算法通过引入稳定性因子的方法,在训练过程中改变竞争层神经元的更新,使LVQ2能够正确收敛。该算法的改变之处是,如果“获胜神经元”和“次获胜神经元”的线性输出标签与样本一致时,对学习率参数α添加一个稳定性因子m,使得学习率变为β=mα,(0.1 算法3:LVQ3算法 输入:样本集D={(x1,y1),(x2,y2),…,(xm,ym);竞争层神经元个数q;学习率α;稳定因子m 输出:更新权重W (1)对权重矩阵W进行随机初始化,为学习率α初始化赋值,初始化稳定性因子m。 (2)将输入特征向量X=(x1,x2,…,xm)输入到输入层,抽取第i个训练样本xi,计算第j个神经元与样本xi之间的欧几里得距离 (21) (3)找出与样本xi距离最小的竞争层神经元j,k,记其输出的类型标记为cj,ck。 (5)如果cj=yi,则权重更新如下 (22) 否则,如果ck=yi,则权重更新如下 (23) (6)如果dj≤dk,则执行(7),否则执行(8)。 (7)如果cj=yi,则权重更新如下 wij=wij+β(xi-wij) (24) 否则 wij=wij-β(xi-wij) (25) (8)如果cj=yi,则权重更新如下 wik=wik+β(xi-wik) (26) 否则 wik=wik-β(xi-wik) (27) (9)一种重复(2)至(8)直到满足设定的迭代次数T或者设定的误差精度e位为止。 LVQ学习算法具有构造简单、收敛快速等优点。LVQ神经网络只需要简单计算输入样本和竞争层神经元的距离就可以完成样本类别的划分,十分适用于流水线式的分类场景,因此被广泛应用于工业模式识别当中。 本部分实验分为“压缩机噪声信号分析与特征提取”和“压缩机声纹模型训练与识别”两组。实验一对压缩机噪声数据进行了时频分析与提取MFCC特征向量,实验二分别采用了3种LVQ学习算法训练LVQ神经网络,并对比分析了其结果。实验采集了100台压缩机的声音数据,其中50台为故障压缩机,类标记为1,另外50台为正常工况压缩机,类标记为0,采样时间为10 s,采样率为50 kHz。数据被分为训练集和测试集,训练集含有80个样本数量,其中40个为故障压缩机的声音数据,另外40个为正常压缩机的声音数据。测试集样本数为20,其中有10个故障压缩机的数据,10个为正常压缩机的数据。实验的硬件配置为Intel core i7四核CPU,主频2.8 GHz,内存16 GB,Nvidia GTX1060显卡,显存6 GB。软件配置为Windows 10操作系统,MathWork Matlab 2018b,Scikiti-learn 0.22。 参考文献中对声音信号的分析方法,对压缩机噪声信号进行时频分析。限于篇幅原因,本文选取了一台工况正常压缩机和一台故障压缩机的结果进行详细解释。图4为正常压缩机的声波图和频谱图,图5为故障压缩机的声波图和频谱图。 图4 1号正常压缩机时频图 图5 1号故障压缩机时频图 从上述两台压缩机的时频分析图中可以看出,故障压缩机声音信号的频率在20 000 Hz以下有明显增大,特别是在13 000 Hz到18 000 Hz以及3000 Hz到5000 Hz之间的频率增大尤其明显。由此可见,不同工况的压缩机声音信号存在着明显差异,进一步验证了通过压缩机声音信号进行故障诊断的可能性。 应用上文中介绍的MFCC特征向量提取方法,分别对压缩机声音信号样本进行特征提取。实验中设分帧帧长为500 ms、重叠率40%,提取24维MFCC特征向量。图6是一台正常压缩机提取的MFCC特征向量,图7是一台故障压缩机中提取的MFCC特征向量。 图6 1号正常压缩机的MFCC 图7 1号故障压缩机的MFCC 本实验部分是分别运用LVQ神经网络的3种学习算法对训练集压缩机声音信号的MFCC特征向量进行训练,得到3个对应的声纹识别模型。 利用3个不同的声纹识别模型对测试集压缩机声音数据进行识别,并对识别结果分别绘制接收者操作曲线(receiver operating characteristic,ROC)和混淆矩阵(confusion matrix),以分析3个模型识别结果的差异。表1为3种学习算法对应的模型描述。 表1 算法及描述 图8为1号模型混淆矩阵和ROC曲线,该模型在10台故障压缩机中正确识别出了6台,同时将2台正常压缩判断为了故障压缩机,故障压缩机识别的召回率(recall rate)为60%,ROC曲线下面积(area under the curve of ROC,AUC)为0.70。可以看出,该模型有一定识别准确度,但不能达到预期要求。 图8 模型1的混淆矩阵和ROC曲线 图9为2号模型混淆矩阵和ROC曲线,该模型在10台故障压缩机中正确识别7台,将1台正常压缩机进行了错误分类,故障压缩机识别的召回率为70%,AUC为0.8。由此可见,改进的LVQ学习算法确实能提高模型的分类正确率。 图9 模型2混淆矩阵和ROC曲线 图10为3号模型混淆矩阵和ROC曲线,该模型在10台故障压缩机中正确识别出了9台,同时只有1台正常压缩机被错误分类,故障压缩机识别的召回率为90%,AUC为0.80。可见,通过LVQ3算法训练的模型具有更好的识别成功率。 图10 模型3混淆矩阵和ROC曲线 表2给出了通过3种不同学习算法所得到的模型的性能总结。 表2 算法模型总结 通过上述实验可以验证,本文提出的基于LVQ神经网络的压缩机声纹识别模型的有效性。 本文提出的压缩机故障诊断技术相比于传统的压缩机故障诊断技术有以下优点: (1)本文将生物识别技术应用到了压缩机故障诊断,使用了“非接触式”的声纹识别方法是本文的核心创新点。此方法克服了传统压缩机诊断中接触式传感器部署困难、批量采集效率低下等缺点。 (2)在特征提取方面,MFCC系数是一种应用最广的声音特征,具有很好的表征能力,方法步骤简单清晰,提取速度快。 (3)在模型构建方面,LVQ神经网络具有搭建简单、分类效果好、不依赖大数据集、学习速度快等优点。 在压缩机噪声信号分析实验中可以发现,故障压缩机声音信号的频率在20 000 Hz以下有明显增大,特别是在13 000 Hz到18 000 Hz以及3000 Hz到5000 Hz之间的频率增大尤其明显,由此可以判断,压缩机的声音信号在正常工况与故障工况时有明显差别,为声纹识别提供了可能性。在模型建立与识别阶段,本文对比了3种LVQ神经网络的学习算法,从结果可以看出使用改进的LVQ学习算法LVQ3所训练出来的模型具有最好的分类效果,召回率达到90%,充分验证了本文提出的故障压缩机诊断方法的有效性。 对于压缩机故障种类的划分与识别,需要投入更多的人力分析故障原因,获取更多故障种类的声音数据。这将是作者下一阶段的科研任务。
2 实验与分析
2.1 实验一:压缩机噪声信号分析与特征提取


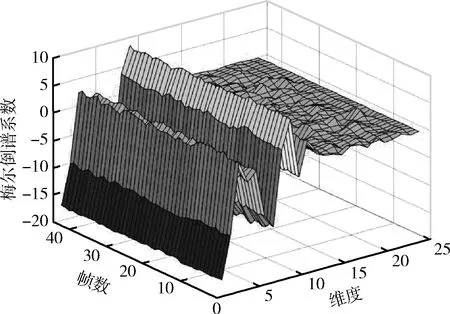

2.2 实验二:压缩机声纹模型训练与识别




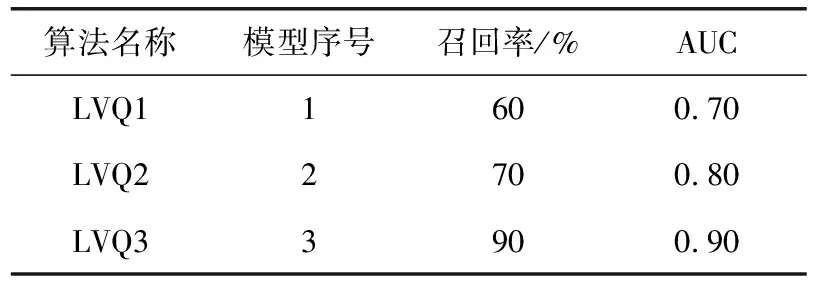
3 结束语

