微机电系统压电振动台迟滞补偿方法研究
郝 瑞 彭 倍 周 吴
电子科技大学机械与电气工程学院,成都,611731
0 引言
MEMS加速度传感器在导航定位[1]、国防安全[2]、智能机器人[3]等领域被广泛应用,然而长期存储和远距离运输的加速度传感器会出现零位与标度因数漂移误差[4],严重影响传感器的测量精度。为保障传感器测量的准确性,通常需要在加速度传感器使用前进行一次重新标定来修正漂移误差[5]。这就要求标度过程能够简单方便且即时有效地在现场实施,而MEMS振动台作为一种可移动的机械平台,能够提供持续稳定的简谐振动来实现对加速度传感器的片上物理激励[6],以振动加速度[7]作为参考运动来获取传感器的零位和标度因数[8]。目前密歇根大学设计的最大加速度为0.3g(g为重力加速度)的压电微振动台[9]可用于商用微惯性测量单元的现场快速重新标定,实现标度因数漂移小于0.02%;康奈尔大学设计的采用光学测距系统进行闭环控制的压电微振动台[10],其本身的长期稳定性可以维持在满量程的0.01%;中国物理工程研究院设计的压电微振动台[11],其加速度的输出范围可达±16g。然而,压电振动台的压电材料具有明显的迟滞特性,导致振动台振动加速度存在误差,严重影响传感器的标定精度[12],因此需要对振动台压电材料迟滞引起的误差进行补偿。
压电迟滞补偿方法主要包括建立迟滞模型来预测迟滞量并通过模型逆向求解补偿电压的前馈控制方法,以及观测当前位移输出预测下一时刻的迟滞量并进行补偿的控制方法。这些方法对迟滞模型的精度要求较高,同时还涉及复杂的参数识别过程。如基于双曲正切函数的动态Preisach模型[13]利用神经网络才能完成动态Preisach模型的参数识别;而改进的Maxwell模型[14]可以描述非对称的迟滞现象,但修改了基础迟滞单元的特性导致参数识别过程复杂;此外,基于Bouc-Wen迟滞模型的前馈线性化控制方法简化了Bouc-Wen模型的参数识别过程,但要求迟滞位移在线观测器对压电执行器的迟滞位移进行精确观测[15];而基于最小二乘支持向量机的压电作动器迟滞非线性模型是利用Preisach模型和最小二乘支持向量机的混合建模法来构建,参数识别过程同样繁琐[16]。另一种方法是将系统的迟滞看作随机扰动,设计具有反馈的非线性控制器来抑制扰动引起的误差[17],这种方法通用性强,易于实现,但不能根据压电执行器的特点做针对性的补偿,控制精度无法满足传感器标定需求。
本文采用前馈控制和反馈控制相结合的复合控制方法[18-19]来实现振动台的驱动和复合控制。前馈控制器采用多项式拟合的迟滞模型,其参数识别简单[20],结合PID反馈控制器能够实现压电执行器的迟滞补偿[21]。
1 MEMS压电振动台迟滞模型的建立
MEMS压电振动台的制作步骤详见文献[22],它由四个相同的L形压电梁和中心平台组成,如图1所示。其中,L形压电梁由上层压电陶瓷和下层硅组成,压电陶瓷的上下表面为金属电极,如图2所示。梁在合理的电压加载下产生变形,驱动振动台做面外平动及定轴转动。加速度传感器在标定过程中固定在中心平台上,与平台一起做简谐振动。

图1 未封装的MEMS压电振动台照片Fig.1 The unencapsulated MEMS piezoelectric vibratory platform
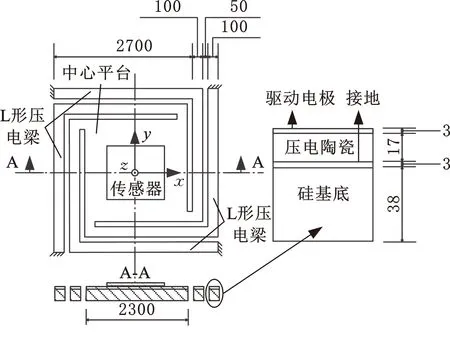
图2 MEMS压电振动台结构(单位:μm)Fig.2 The structure of MEMS piezoelectric vibratory platform(unit:μm)
振动台面外振动原理如图3所示,图3a为压电振动台变形示意图。当给内圈压电梁施加电压U(U=asinωt),给外圈压电梁施加电压-U时,中心平台和加速度传感器沿z轴方向做简谐振动。提取振动台中心O点位移发现,其波形存在迟滞现象,可能是由压电材料的压电迟滞特性引起,因此建立基于多项式拟合的迟滞模型对迟滞现象进行分析。Maxwell迟滞模型指出迟滞包含线性部分和迟滞部分[23],三次模型是描述机械系统迟滞非线性的模型之一,迟滞函数f(U)[24]如下:
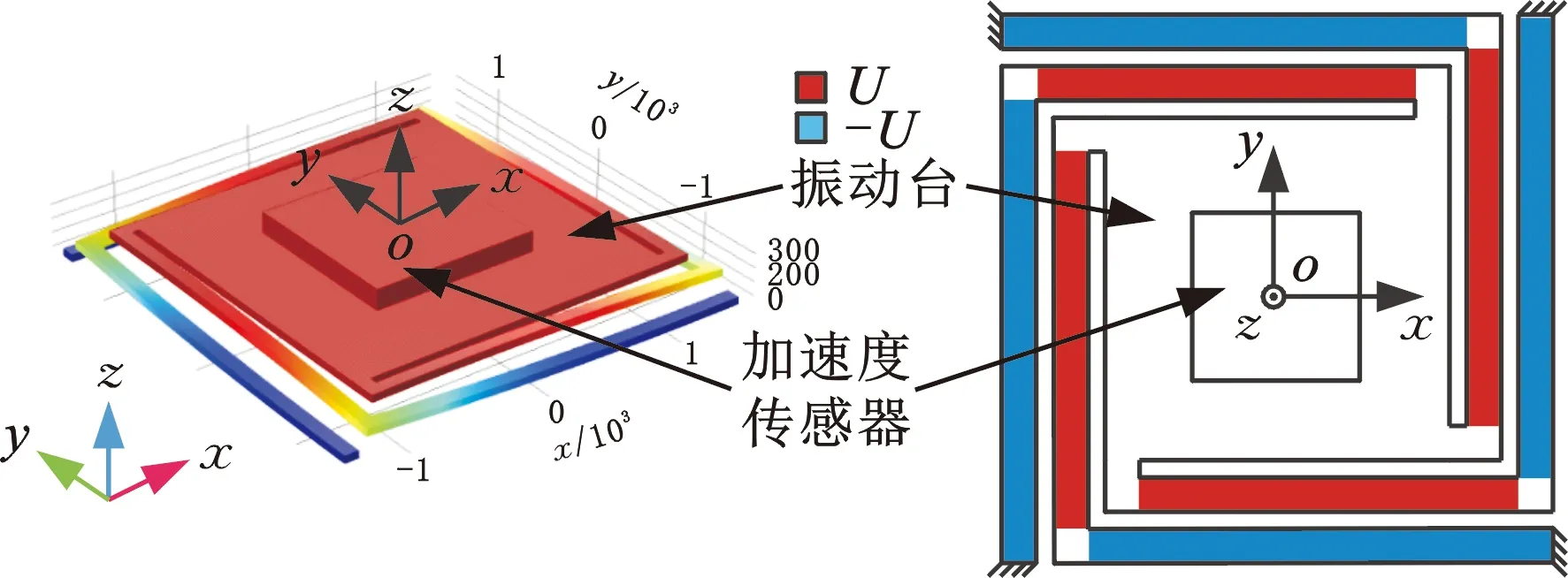
图3 MEMS压电振动台面外振动变形示意图Fig.3 The out of plane deformation of MEMS piezoelectric vibratory platform
f(U)=KsU-αU3+β(U′)3
(1)
式中,U′为驱动电压导数,迟滞环线性部分为等式右边第一项;Ks为线性部分系数;α、β为迟滞部分待拟合参数。
绘制量纲一电压-位移迟滞环图像,如图4、图5所示。压电陶瓷电压-位移迟滞环[25]表示对压电陶瓷在极化方向上施加周期变化的电场,压电陶瓷的变形量随电场变化周期性改变,交变电场由施加在驱动电极上的电压控制,电压上升段和下降段压电陶瓷变形量不同导致压电振动台的电压-位移曲线呈环形。同一电压下,压电陶瓷的变形量在电压上升段和下降段之差为d,如图4所示,它的大小可以描述压电陶瓷的迟滞量,通过改变参数β可以控制压电陶瓷的迟滞量。同时,根据压电陶瓷迟滞成因分析[26]得出压电陶瓷非180°电畴转向的不完全可逆是造成压电陶瓷执行器迟滞的根本原因,而不同的压电陶瓷中非180°电畴的数量、分布不同,影响迟滞环的形状,参数α可以描述迟滞环的形状变化[27],如图5所示。
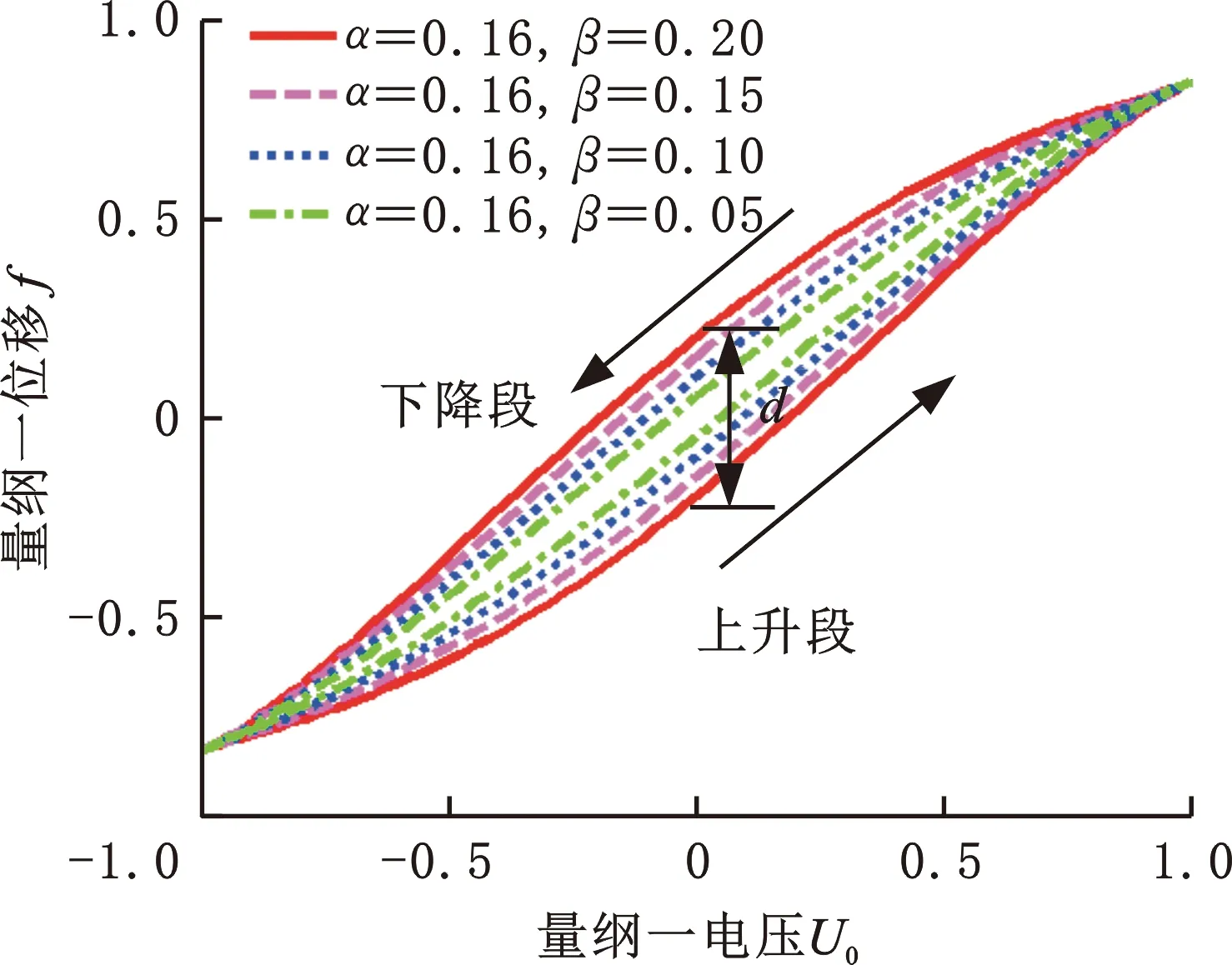
图4 电压-位移迟滞环(α不变)Fig.4 Dimensionless hysteresis loop(α unchanged)
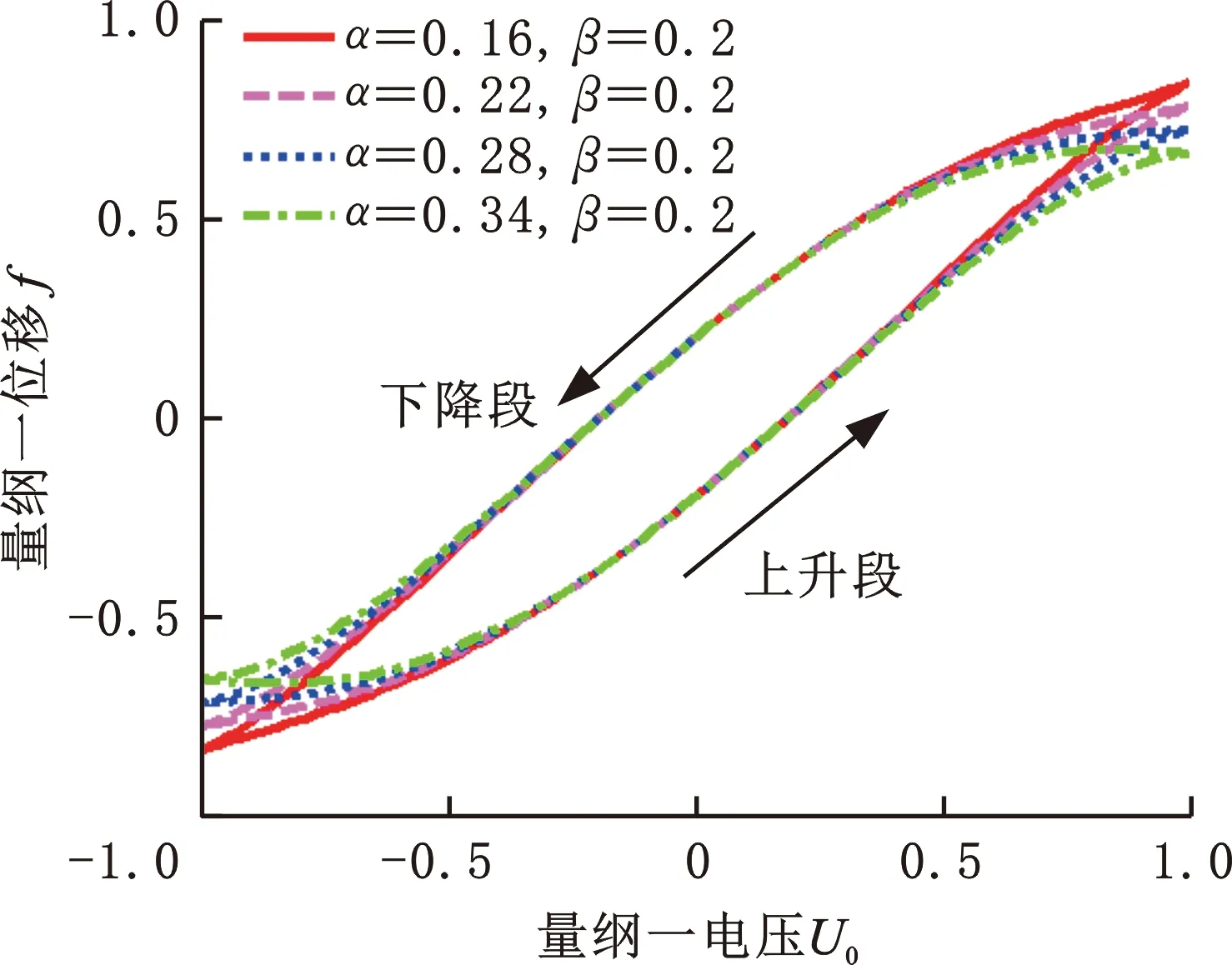
图5 电压-位移迟滞环(β不变)Fig.5 Dimensionless hysteresis loop(β unchanged)
通过参数拟合可以得到参数α、β,并得到MEMS压电振动台的电压-位移迟滞环,如图6所示。图6为压电振动台在10 V(317 Hz)正弦电压激励下平稳振动后提取一个周期内压电振动台的电压和振幅数据进行参数拟合的曲线,拟合结果为Ks=1.46×10-6,α=0.411×10-6、β=1.19×10-6。
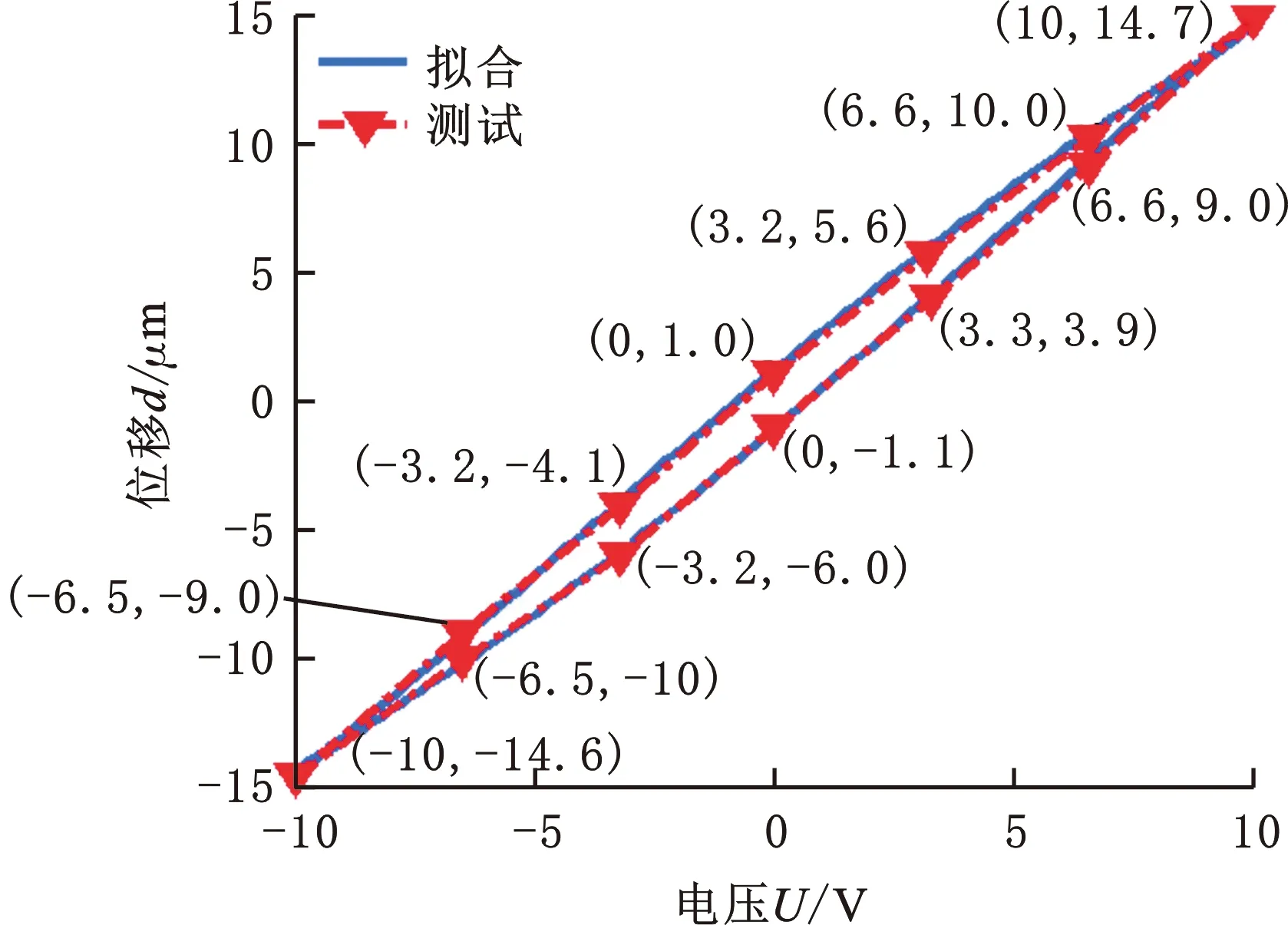
图6 MEMS压电振动台拟合迟滞环Fig.6 Dimensionless hysteresis loop fitting of MEMS piezoelectric vibratory platform
2 MEMS压电振动台复合控制
根据振动台机电耦合模型[22],等效驱动力是驱动电压的线性函数,设比例系数为Kf,则振动台的振动方程可写成
(2)
式中,y(t)为振动台的位移;M为等效质量;C为阻尼系数;K为刚度系数,ΔU为驱动电压的幅值。
振动微分方程可以写成离散的状态空间形式,即
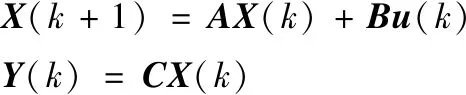
(3)
式中,X(k)为系统在t=kT时的状态向量,k=0,1,2,…;T为采样周期;u(k)为输入向量;Y(k)为输出向量;A、B、C分别为状态矩阵、输入矩阵和输出矩阵。
压电振动台复合控制原理如图7所示。图7中u(kT)表示复合控制器的控制量,由前馈控制器的控制量uFF(kT)和反馈控制器的控制量uFB(kT)组成[28]。按照文献[29]设计前馈控制器,由于前馈控制器抵抗扰动的能力较弱,其扰动可能引起补偿过度使控制效果降低[30],为此引入函数G(k)来限制前馈控制器的补偿量:

图7 MEMS压电振动台控制原理框图Fig.7 The control block diagram of MEMS piezoelectric vibratory platform
(4)
式中,δk为k时刻前馈控制器最大补偿量。
则复合控制器的控制量u(kT)可以表示为前馈控制量和反馈控制量的叠加:
u(kT)=G(k)uFF(kT)+uFB(kT)=
G(k)uFF(kT)+uFB(kT-T)+
KP[e(kT)-e(kT-T)]+KIe(kT)+
KD[e(kT)-2e(kT-T)+e(kT-2T)]
(5)
式中,KP、KI、KD分别为PID控制器的比例系数、积分系数和微分系数;e(kT)为偏差。
由于k时刻驱动电压为u(kT),则通过位移传感器得到振动台位移为y(kT)。采用压电迟滞模型预测k+1时刻振动台的预测位移yp(kT+T)以及期望位移yr(kT+T),则位移补偿量φ(kT+T)等于期望位移yr(kT+T)减去预测位移yp(kT+T),而最大电压补偿量δk与位移补偿量φ(kT+T)存在线性关系:
δk=γφ(kT+T)
(6)
式中,γ为比例系数。
在有扰动的情况下,前馈控制量uFF(kT)被限制避免过度补偿,反馈控制器依然能够保证在前馈控制量被限制的情况下实现振动台的连续控制。采用Simulink来仿真补偿结果,输入信号为10 V(317 Hz)的正弦电压,仿真结果如图8、图9所示。仿真结果表明,函数G(k)存在时补偿效果优于不包含限制函数G(k)的迟滞补偿效果。
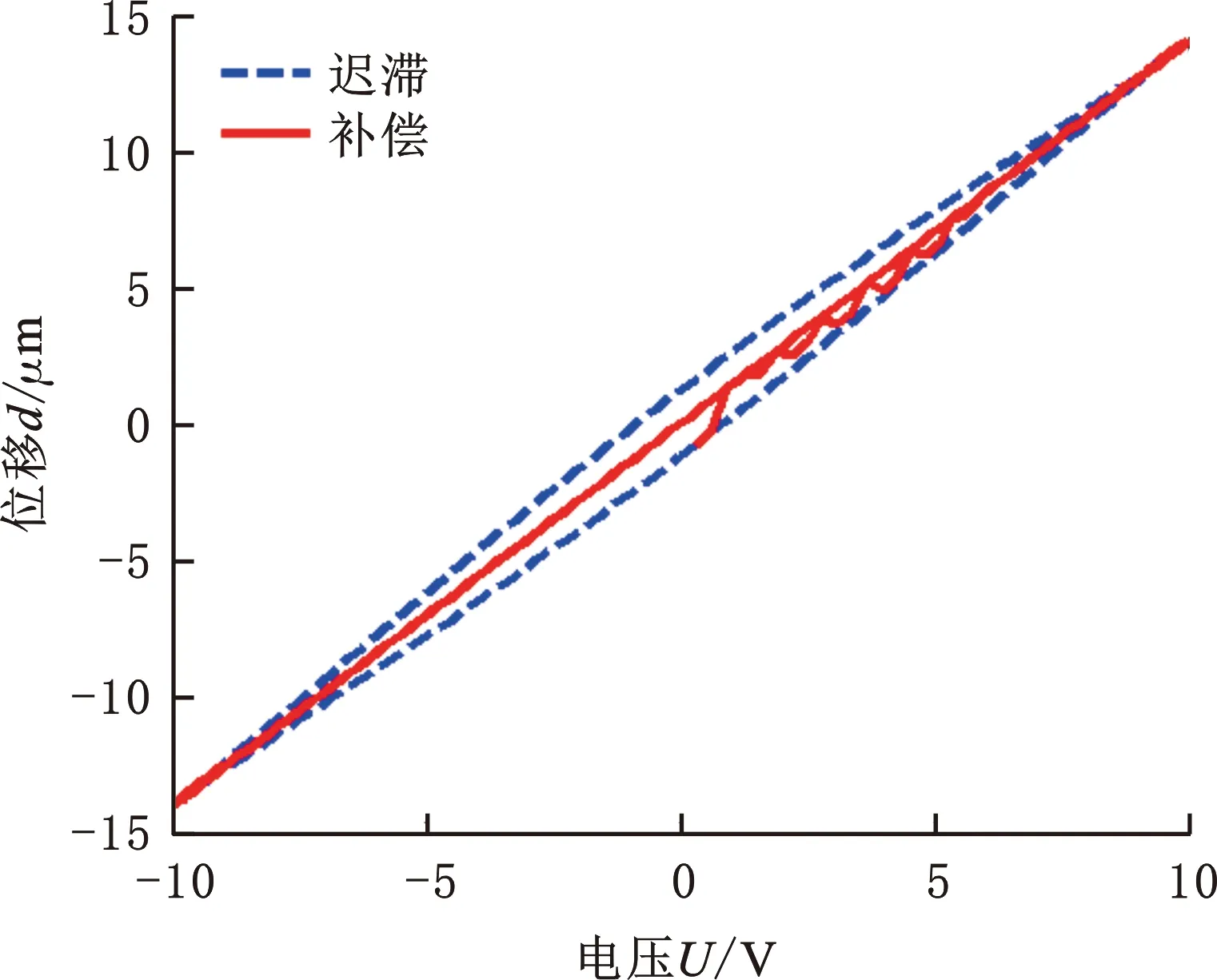
图8 不增加G(k)情况下振动平台电压-位移曲线Fig.8 The voltage-displacement curve of vibratory platform without G(k)
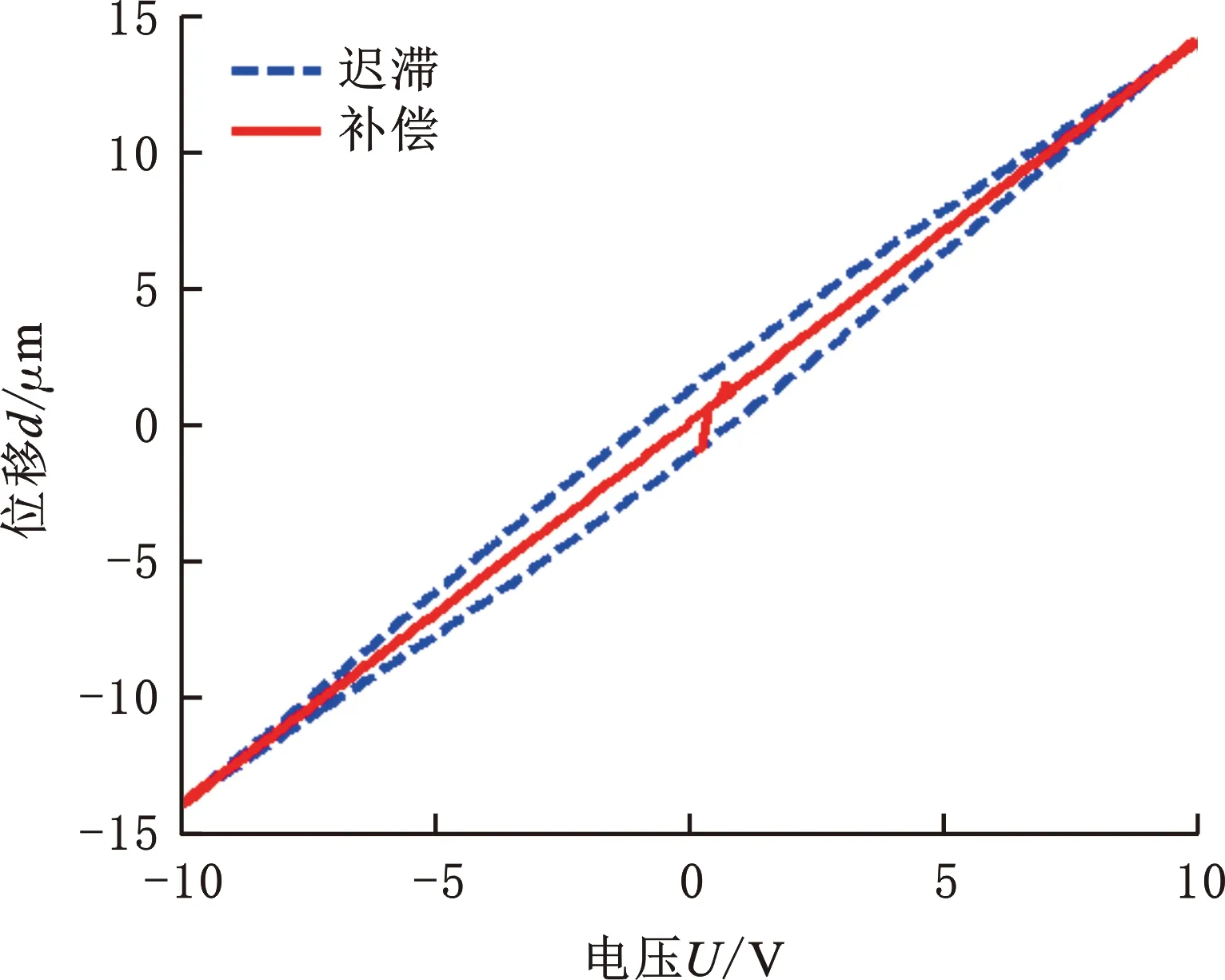
图9 增加G(k)情况下振动平台电压-位移曲线Fig.9 The voltage-displacement curve of vibratory platform with G(k)
3 实验验证
完成电路设计,搭建振动台位移检测实验平台如图10所示。实验平台由定位台、固定架、压电振动台、位移传感器和控制电路组成。振动台位移检测原理是:通过垂直腔面发射激光器(SS85-5U001)向振动台表面发射激光束,激光束被振动台表面的反光层反射后,由若干分布在不同位置的光敏二极管(SP85-4N001)接收并检测光强,不同位置的光敏二极管接收到的光强不同,通过几何光学方法得到振动台与位移传感器之间的距离[7],如图11所示。

图10 MEMS振动台位移检测实验平台Fig.10 MEMS vibratory platform displacement detection experimental platform
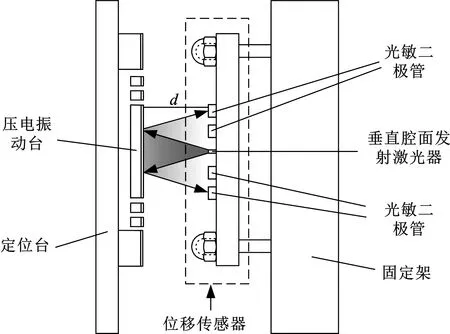
图11 MEMS振动台位移检测原理图Fig.11 The schematic diagram of MEMS vibratory platform displacement detection
光学位移检测系统的检测范围为0~500 μm,分辨力可以达到0.15 μm。实验采用10 V(317 Hz)的正弦电压驱动,补偿前后振动台时间-位移曲线见图12。补偿前振动台位移与期望位移的最大误差为1.8 μm,而补偿后振动台位移与期望位移间最大误差小于位移传感器的灵敏度0.15 μm。

图12 MEMS压电振动台时间-位移曲线Fig.12 The displacement curve of MEMS vibratory platform
图13为补偿前后的振动台时间-加速度曲线,补偿前振动台加速度与期望加速度的最大误差为1.3g,补偿后振动台加速度与期望加速度的最大误差为0.05g。
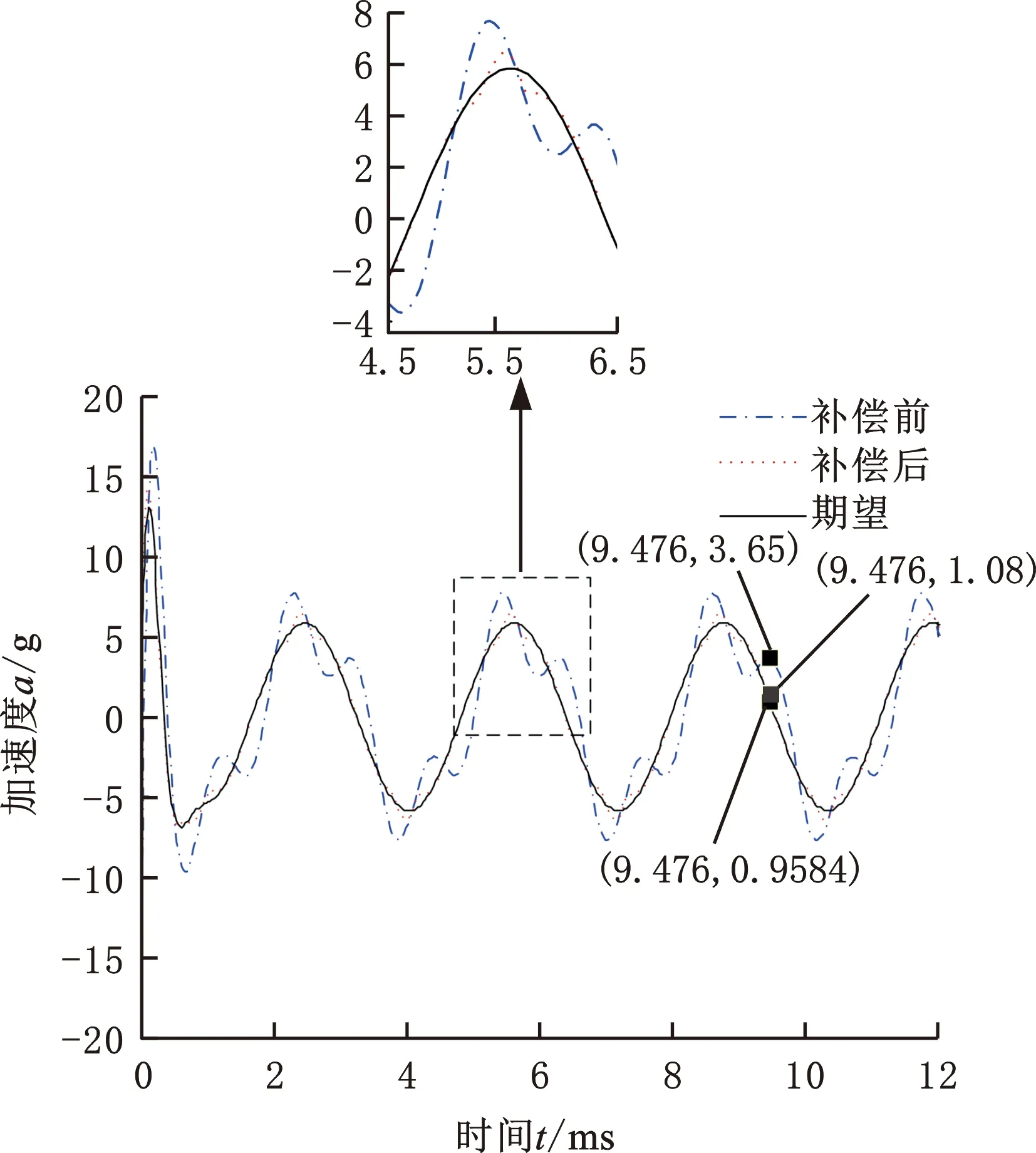
图13 MEMS压电振动台时间-加速度曲线Fig.13 The acceleration curve of MEMS vibratory platform
补偿后振动位移误差为1.8 μm,振幅为14 μm,相对误差为12.8%,振动加速度误差为1.3g,振动台提供的最大加速度为6.5g,相对误差为21.6%,采用迟滞补偿控制后振动台位移相对误差为1.07%,加速度相对误差为0.7%。结果表明压电陶瓷迟滞效应是引起压电振动台振动位移和振动加速度误差的重要原因之一。
同时增加前馈控制器阈值函数G(k)可以有效地提高补偿效果,图14为振动台在补偿前后电压-位移对比曲线,可以看出,增加前馈控制器阈值函数G(k)后,补偿结果优于未增加阈值函数G(k)的结果。
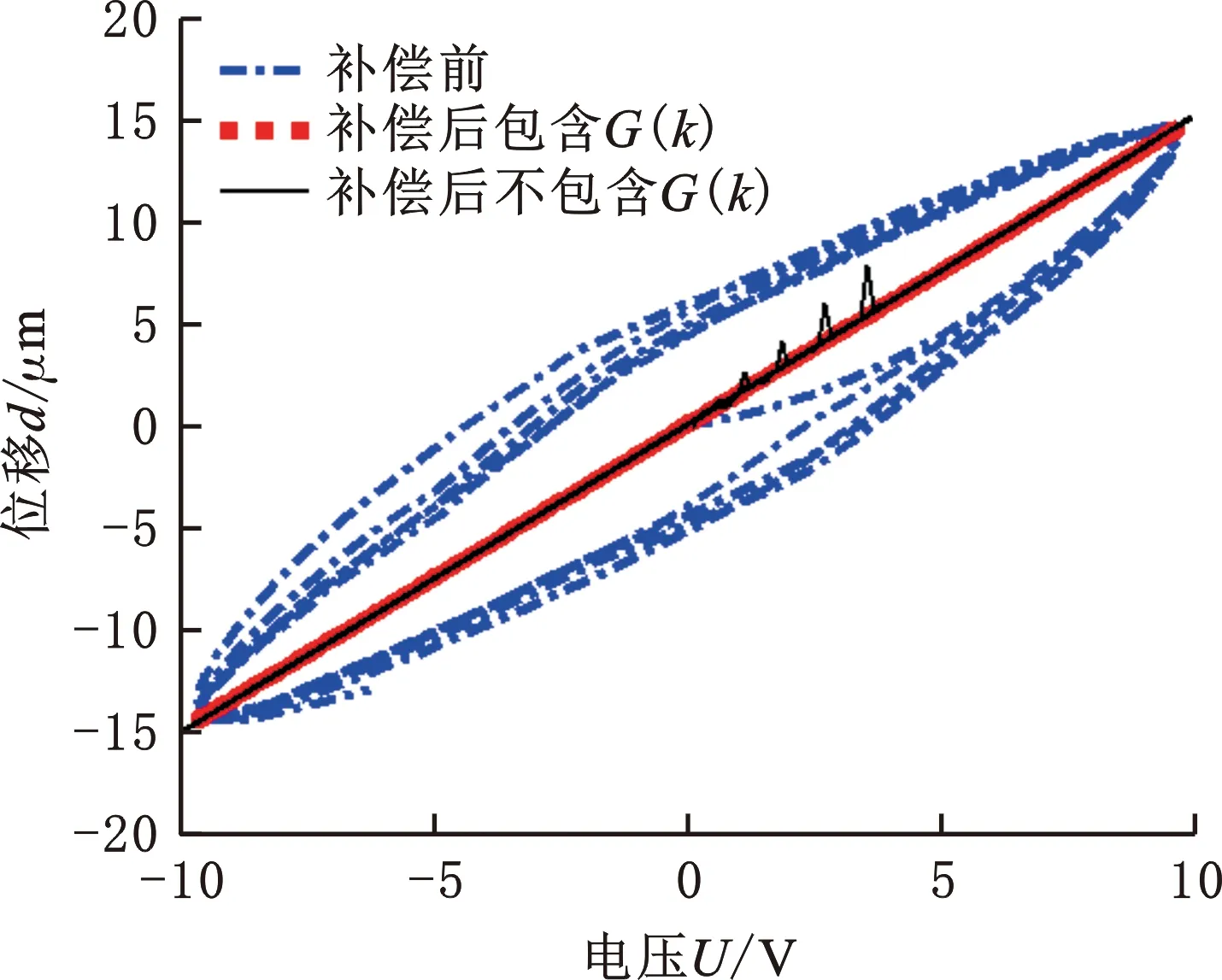
图14 补偿前后MEMS压电振动台电压-位移曲线Fig.14 The voltage-displacement curve of MEMS vibratory platform before and after compensation
4 结论
(1)振动台时间-位移曲线的迟滞现象主要由压电材料的迟滞特性引起。
(2)振动台的振动位移迟滞引起的误差在微米量级,对振动台振动加速度的影响较为严重。压电迟滞引起的振动台加速度误差为1.3g,振动台提供的最大加速度为6.5g,其相对误差为21.6%。
(3)基于多项式拟合的迟滞建模方法能够在避免复杂参数识别的情况下对压电振动台的迟滞进行较准确的描述。
(4)复合控制方法适用于MEMS压电振动台的控制和迟滞补偿,并成功将振动台振动加速度误差从1.3g降到0.05g,相对误差降低到1%以内。

