数值堆材料辐照损伤并行动力学蒙特卡罗软件MISA-AKMC的设计与实现

储根深，何远杰，白 鹤，陈丹丹，任 帅，贾丽霞，吴 石，贺新福，杨 文，胡长军

(1.智能超算融合应用技术教育部工程研究中心，北京 100083；2.北京科技大学，北京 100083；3.中国原子能科学研究院，北京 102413)

材料辐照损伤模拟是数值堆软件的重要内容，采用多尺度模拟方法是研究材料辐照损伤问题的一个重要手段[1-6]。其中，动力学蒙特卡罗(KMC)方法是多尺度模拟中最为重要的方法之一，被广泛用于研究微观尺度的材料演化行为。不同于同样原子尺度的分子动力学(MD)方法，KMC方法将原子运动轨迹粗化为体系组态跃迁，使该方法可在保持原子级别精度下有效将模拟的时间跨度从原子振动的尺度提高到组态跃迁的尺度，即实现秒甚至年量级的材料辐照行为模拟[7-9]。

KMC方法目前已有不少研究[10-19]，包括原子动力学蒙特卡罗(AKMC)方法、实体动力学蒙特卡罗(OKMC)方法、事件蒙特卡罗(EKMC)方法等。其中，AKMC方法以原子为基本对象，考虑原子和缺陷之间的跃迁导致的微结构演化行为，其在空间尺度上更精确且方便与同样以原子为操作对象的MD方法进行耦合。但在面向实际应用需求时，其仍面临着内存限制和复杂的计算量等挑战。随着模拟体系的增大，模拟所需内存需求的矛盾也开始凸显出来。同时，虽然KMC模拟在时间尺度上相对于MD提升了数个数量级，但计算过程仍十分耗时，特别是在大体系模拟时。解决计算和内存的双重矛盾最有效的方式就是并行化，通过计算任务分配以并行计算，并通过分布式内存方案减少单个节点上的内存占用。基于此，本文将采用AKMC方法设计数值堆材料辐照损伤动力学并行模拟软件MISA-AKMC。

1 KMC方法与KMC并行化研究

和通用的蒙特卡罗思想类似，KMC方法的核心思想是随机抽取事件。若可确定体系当前状态下所有可能发生的事件及其发生的概率，即可将以这些事件发生的概率作为权重随机抽取事件执行以改变体系的状态，以此推进体系向前演化。图1示出了一种通用的KMC执行流程，其在时间步循环内，一次计算所有可能的事件的跃迁速率(也即事件概率)，随后通过随机数选择其中的1个事件，并行执行该事件；如此进行时间步的循环，即可推进系统向前演化，直到模拟到预期的时间。在材料微观演化模拟过程中，事件可以是缺陷的位置跃迁或新缺陷的生成等。

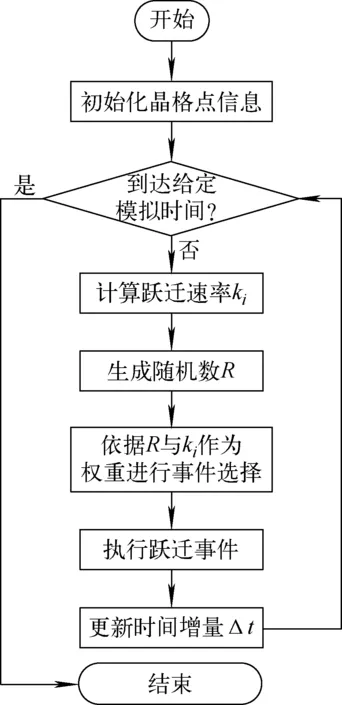
图1 KMC执行流程Fig.1 KMC execution process

由于串行的KMC中，体系完成的连续两次演化是独立、无记忆的，这个过程是一种典型的马尔可夫过程(Markov process)。且计算两个相邻的事件之间具有依赖关系，即事件的发生是串行的，位于当前状态的体系只发生1个事件，该事件发生且执行完成后才会进入到下一个事件的发生过程。这种依赖性给KMC并行化带来了很大阻碍。

目前大多数已有的并行KMC方法基本是基于区域分解的，将模拟区域划分为多个子区域，并将其分配到不同的计算单元上。同时，这些方法近似认为这些子区域之间的距离足够远，之间的相互影响不大，因此不同子区域上的事件可同时发生。这就是现有的基于空间分解的并行KMC算法的基本思想。典型的并行KMC算法有基于空间分解方案的SL(sub-lattice)KMC[20-21]、SP(synchronous parallel)KMC[22-24]、SR(synchronous relaxation)KMC[25-26]等。其中，SP KMC算法和SR KMC算法在执行过程中，每个时间步均需引入昂贵的全局通信，影响计算性能；而SL KMC算法执行过程不必全局通信，这也成为本文的并行KMC算法的首选。

在SL KMC算法中，为实现正确的并行计算，需解决两个问题：1) 边界处的事件冲突；2) 不同计算单元上的时间同步(实际上，在其他两种并行SP KMC和SR KMC算法中，也存在这两个问题)。为解决边界处的事件冲突，一般采用子区域着色方法。其将每个计算单元上的子区域再分为多个扇区，不同位置的扇区标记为不同颜色，且不同计算单元中处于同一位置的扇区标记为相同颜色。通过着色使相同颜色的扇区在空间上不相邻。各计算单元均依次选择相同颜色的扇区进行计算。KMC并行中的事件冲突问题如图2a所示，当两个计算单元上的事件发生在边界处的邻近位置时，可能会产生事件冲突。为解决这种冲突，可针对计算单元对应的子区域划分扇区并着色。着色算法解决事件冲突如图2b所示，图中的一维着色示例，黄色与橙色的扇区分别被间隔开来，依次选择黄色扇区和橙色扇区进行计算。当然，在实际程序中，考虑到模拟的三维空间和计算单元的三维逻辑分布，将每个计算单元内对应的子区域划分为8个扇区，分别着色为S0、S1、…、S7，如图2c所示。针对不同计算单元上的时间同步问题，SL并行KMC方法采用时间阈值的方式。给定时间阈值T，各计算单元上进行各自的KMC演化模拟，直到计算单元中当前扇区的时间增量达到阈值。在时间增量达到阈值后，即可与邻居进程进行通信以交换数据(如同步跃迁对邻居进程的更改，从邻居进程处同步ghost区域等)。通信完成后，各计算单元切换到下一扇区，进行下一扇区的计算模拟，直到计算单元上的总时间增量达到阈值2T，如此往复。通过该时间阈值，计算单元在其时间增量到达nT时进行通信(其中n为正整数)，通信完成后进行下一扇区的模拟(同一计算单元上的各扇区的模拟依次进行)。

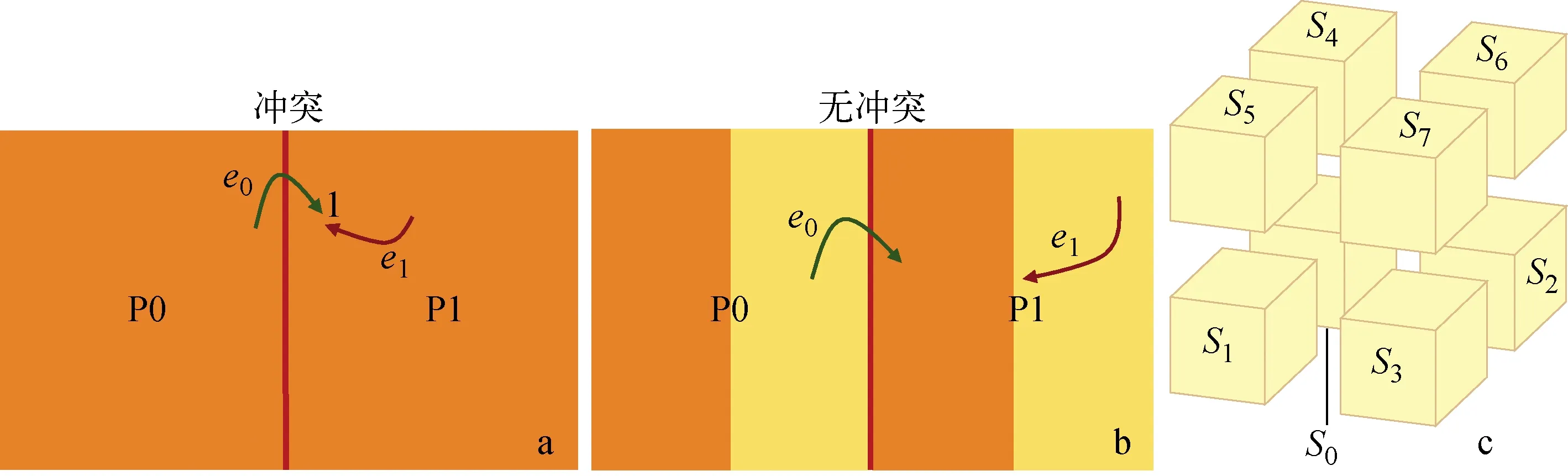
图2 KMC并行中的事件冲突(a)、着色算法解决事件冲突(b)和三维空间上的扇区划分与着色(c)Fig.2 Event conflict in KMC parallelism (a), solving even conflict by coloring method (b), and sector dividing and coloring in three-dimensional space (c)

2 MISA-AKMC并行KMC框架

图3示出了MISA-AKMC程序及并行KMC框架架构，为便于KMC模型的集成与可扩展，并方便软件的核心优化，将MISA-AKMC并行部分分离开，形成KMC并行框架。该框架采用空间分解的并行思想实现了SL并行KMC方法，并提供额外的接口以供实现其他的并行KMC算法。框架针对核心的并行部分，提供了多种加速优化方法，包括局部跃迁速率更新方法和转发通信算法优化等。此外，框架还内置了晶格点和缺陷存储等数据结构的表示，并向上层模型提供了KMC模型集成接口。

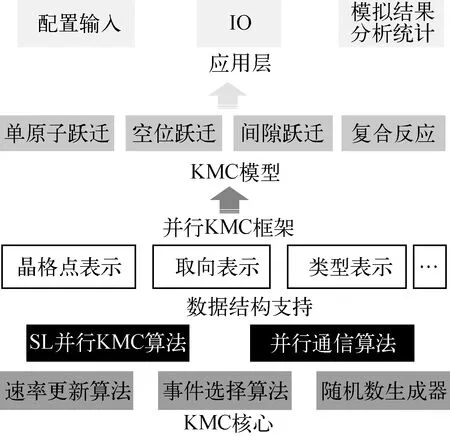
图3 MISA-AKMC程序及并行KMC框架架构Fig.3 Architecture of MISA-AKMC program and parallel KMC framework

2.1 并行sub-lattice 方法实现

作为并行KMC框架的核心部分，本文实现的sub-lattice并行KMC算法计算流程如图4所示。在本文的sub-lattice算法实现中，先依据通信阈值T计算出通信次数n，以此进行外层的时间步循环。在时间步循环内部，依次进行计算单元内的8个扇区的迭代：1) 扇区内的事件循环，对于每个扇区，重复在该扇区选择并执行时间，直到该扇区的时间增量达到预设的阈值T；2) 通信，在一扇区s的计算完成后，还需进行通信以准备下一个扇区的计算，包括将扇区s对邻居计算单元上的更改通信给邻居计算单元，同时为计算下一扇区，还需从邻居计算单元上通信获取下一扇区的ghost区域；3) 进入下一扇区的计算。

图4 MISA-AKMC并行KMC框架中的并行算法流程Fig.4 Parallel algorithm flow in parallel KMC framework of MISA-AKMC

2.2 并行框架优化

为进一步提升MISA-AKMC程序性能，本文还针对其中核心并行部分进行了优化。需强调的是，由于MISA-AKMC采用并行算法和计算模型分离的设计，针对并行框架部分的优化和改动不会影响到KMC模型部分的实现，这是本文设计的KMC程序的一大优势。

1) 局部更新优化

为模拟的精确性，将通信阈值T取得较小，一般近似的等于单次事件产生的时间增量。这必然导致扇区内的事件循环中事件发生的数量很少，这些事件影响的区域也有限。故不必在每个事件发生后“全局地”更新该扇区的跃迁速率，而只需更新上一个事件影响的区域内的跃迁速率。计算跃迁速率是KMC模拟中最耗时的，通过局部跃迁速率更新的优化方法，可极大减少更新跃迁速率的计算开销。

考虑到单次跃迁影响区域可能覆盖到其他扇区，甚至其他计算单元对应的区域，如图5所示。所以，事件发生后，不仅需更新当前扇区的总跃迁速率，还需更新受影响的其他扇区的跃迁速率和邻居计算单元上对应扇区的跃迁速率。为此，将事件的影响区域划分为3个部分。其中，第1个部分为影响区域和当前计算扇区的交集，记为S；第2部分为影响区域与当前计算单元上但除当前计算扇区以外的区域的交集，记为C；第3部分为影响区域与ghost区域的交集(影响区域不会超过ghost区域的边界)，ghost区域是计算单元模拟区域外面的一层额外区域，但该区域是来自邻居进程上的副本，将该区域记为G。在更新跃迁速率时，针对S区域，直接更新；针对C区域，找到该区域所属的扇区，再更新该扇区的总跃迁速率；对于区域G，先更改ghost区域的状态，后续通信时，将更改同步到邻居进程，再在邻居进程上重新计算这部分受影响区域的总跃迁速率。

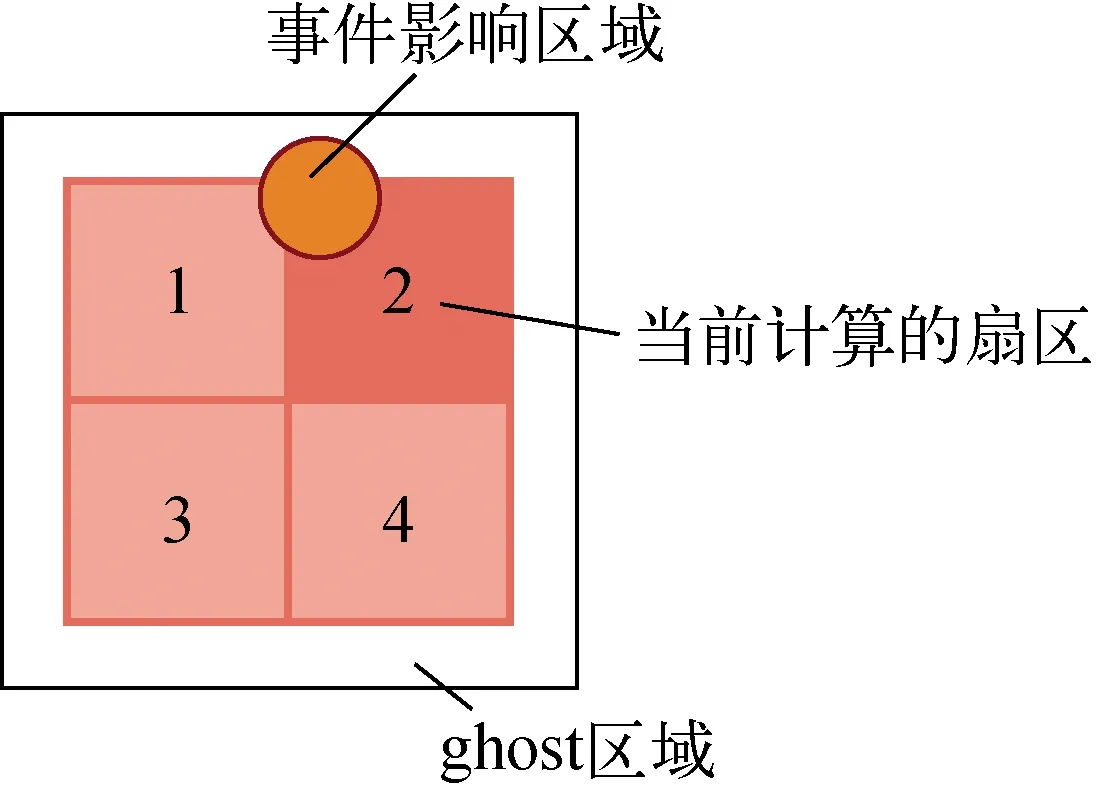
图5 KMC事件的可能影响区域Fig.5 Possible effect region of KMC event

2) 进程通信优化

在三维KMC模拟中，每个扇区与7个邻居计算单元相邻。在图4所示的算法中，针对两个通信过程，每个扇区均与7个邻居计算单元进行通信。直接的通信方式，完成1轮8个扇区的计算，需进行224次通信(7邻居×8扇区×2个通信操作×2(发送/接收操作))，如SPPARKS程序[27]。在Wu等[28]开发的Crystal-KMC程序中，提出了通信合并的方案，在1个扇区计算完成后的同步模拟区域的通信可与下一扇区计算前的同步ghost区域的通信进行合并，这样可将通信次数降为182。

实际上，该方法还可进一步优化：(1) 1轮计算(1轮指8个扇区依次完成各自的计算)的最后1个扇区和下一轮的第1个扇区也可通信合并；(2) 调整扇区的计算顺序，进一步降低通信次数。通过进一步优化，通信次数可降为128。

本文的通信优化方法，采用转发通信的通信策略，实现了更少的通信次数。该方法仅与面相邻的邻居计算单元直接通信，并通过面相邻的进程转发来自角相邻与边相邻的计算单元之间的通信。采用通信转发算法，在1个扇区和7个邻居计算单元通信时，仅需进行3个面相邻的计算单元上的3次通信，即可完成和7个邻居进程的通信。该方法单独使用，可将通信次数从224降为96。进一步地，将转发通信策略配合[28]中的通信合并方法，可将一轮的通信次数降为56，极大地压缩通信次数。本文所采用的通信优化方法是性能和通信策略层面的优化，因此该通信优化方法不会对模拟精度造成影响。

在通信实现层面，并行KMC框架提供了统一的通信抽象层，KMC模型的实现上只需实现给定数据的打包和解包即可。在该通信抽象层中，主要实现了：1) 进程与邻居进程通信，获取其ghost区域数据，并给邻居进程发送对应的ghost区域数据，以支持计算进程边界处缺陷的跃迁速率；2) 进程与邻居进程通信，将运动到进程模拟区域外的缺陷数据发送给邻居进程，并接收从邻居进程发送的运动到该进程的缺陷数据。通过这两个通信步骤，结合高效的通信优化策略，可支持并行KMC模拟中各进程间的数据交换与高效计算。

3 并行框架下的材料演化模型

金属材料的许多性能主要决定于缺陷的类型和浓度，缺陷会改变完美晶体的结构。缺陷中最简单的是点缺陷，包括间隙和空位。目前很多KMC程序只能考虑空位的作用，而缺少间隙的引入。因此，针对并行KMC框架，开发了面向材料辐照微观演化的空位-间隙模型。

针对BCC的晶格结构，定义如下基本KMC反应事件(图6)：1) 空位跃迁，空位可向8个1nn近邻处的原子位置跃迁；2) 间隙跃迁，双原子间隙dumbbell对中的1个原子向8个1nn近邻中的位于同一平面上的4个晶格点跃迁；3) 空位-间隙复合，在空位或间隙跃迁事件发生后，若间隙和空位位于一定范围内，会发生复合反应。

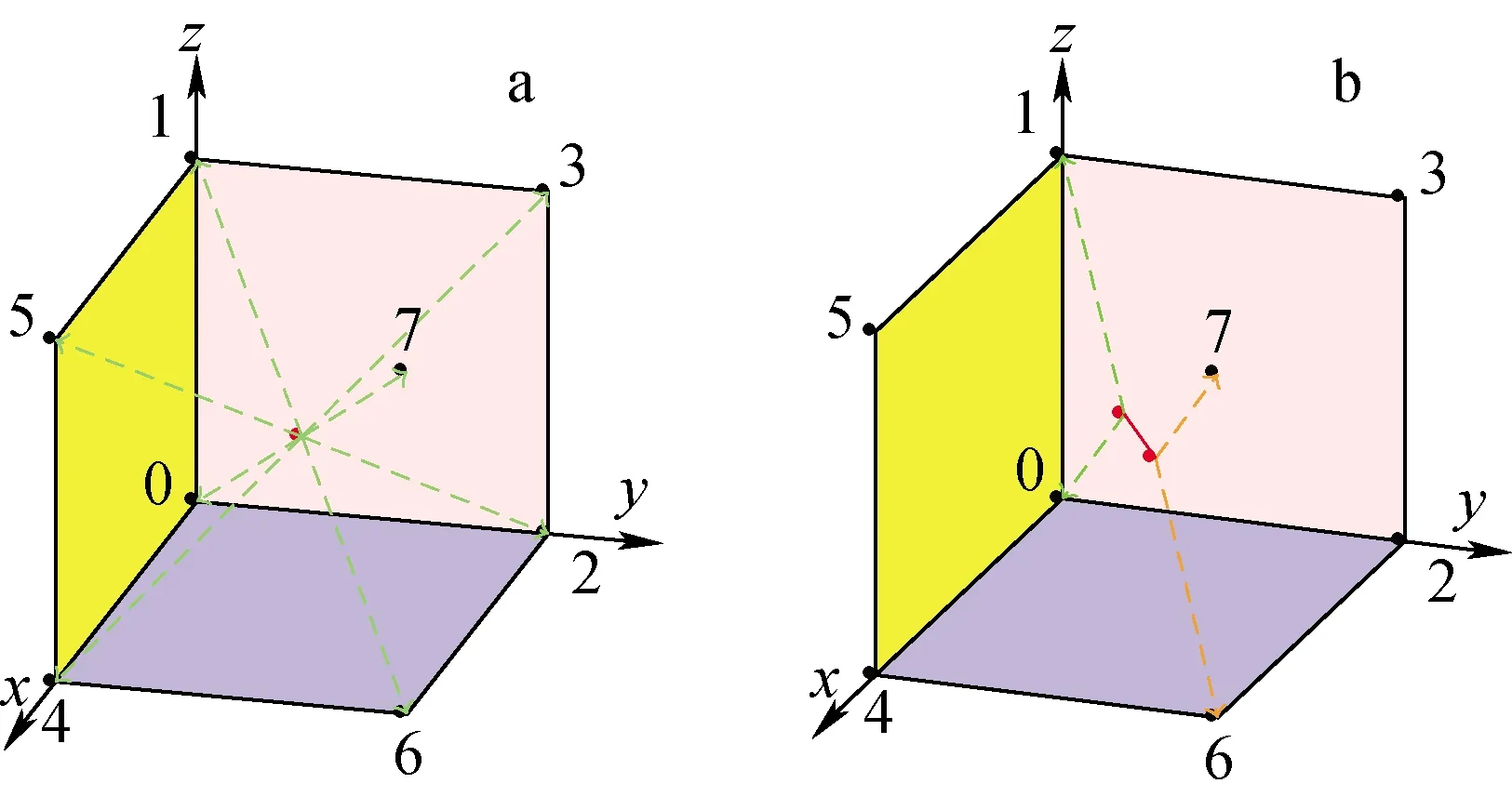
a——空位可向1nn附近的8个邻居晶格点跃迁；b——间隙可向1nn附近的且位于同一平面的4个晶格点跃迁图6 KMC空位-间隙跃迁计算模型示意图Fig.6 KMC model for vacancy-interstitial transition

对于跃迁速率的计算，本文通过Arrhenius方程进行计算：

其中：v为尝试频率；Ef和Ei分别为跃迁后、跃迁前体系的能量；kB为玻尔兹曼常量；T为体系温度；e0与空位近邻处原子类型有关。为计算跃迁前后体系的能量，本文引入势函数的计算方法，包括vicent_2007势函数[10]和EAM势函数[29]。

3.1 模型表示

为高效地基于并行KMC框架进行模型的实现，首先需针对模型中的空位和间隙缺陷进行表示(图7)，并提供事件列表、事件类型的表示。为此，在本模型的实现层面，从框架提供的晶格点索引出发，通过晶格点的id和类型确定对应的晶格点位置是否为缺陷或单原子。针对不同类型的缺陷，如空位或间隙，分别采用列表进行存储，并可通过晶格点id进行索引。其中，列表中的每项包括了该缺陷向周围各不同方向跃迁的速率，对于间隙缺陷，还包括其取向信息。这种表示方式建立起了晶格点与缺陷之间的一一映射，并将缺陷的跃迁速率和跃迁事件统一起来管理与更新，以及通过不同的缺陷列表实现了不同跃迁事件的分类。

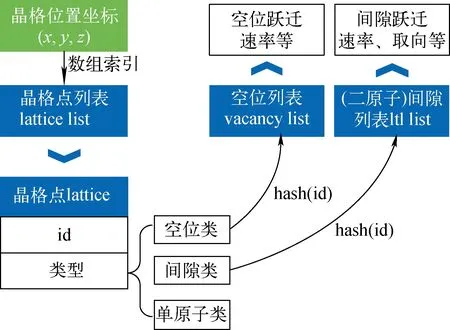
图7 MISA-AKMC中针对间隙和空位缺陷的表示Fig.7 Representation of interstitial and vacancy defects in MISA-AKMC

3.2 模型针对框架接口的实现

为实现KMC模型，需遵循并行KMC框架提供的接口，其中主要包括以下部分的实现：1) 跃迁速率接口，依据给定区域更新该区域的缺陷对应的跃迁速率；2) 通信接口，通信时的数据打包和解包接口。其中，第1个接口的实现为KMC模型的核心，通过势函数计算给定区域内所有缺陷的跃迁速率；第2个接口是通信的必要依赖，数据打包和解包串联起了并行KMC框架内的高效通信算法。由于模型中，晶格点类型和缺陷类型多样，这对高效的通信接口实现提出了挑战。本文采用元数据加字节数据的方式来进行数据打包和解包。在发送的数据包的头部包含通信的元信息，包括需通信的单原子数、空位数和间隙数。在元数据后依次添加需通信的单原子数据、空位数据(如空位id、跃迁速率等数据)和间隙数据。通过这种数据通信方式，可实现将复杂的数据类型进行打包和解包，依赖并行框架获得高效的通信性能。

4 MISA-AKMC测试与分析

4.1 测试环境

对MISA-AKMC的测试均在曙光超算平台上进行，仅使用了其中的CPU核，系统配置和环境列于表1。

表1 曙光超算平台的相关参数Table 1 Parameter of Sugon supercomputer

4.2 正确性验证

为验证开发的并行MISA-AKMC程序的正确性和有效性，选用表2中数据对Cu团簇析出过程进行验证。模拟采用MPI单进程进行，依据SL KMC算法将每个进程划分为8个扇区。

表2 Fe-Cu-V(铁-铜-空位)体系模拟算例的输入参数Table 2 Input parameter of simulation case for Fe-Cu-V (iron-copper-vacancy) system

在模拟过程中，统计不同时刻孤立的溶质Cu原子浓度和数量，并与相同输入条件下的其他文献[30]中的KMC模拟结果进行对比，如图8所示，其中的蓝色曲线为MISA-AKMC模拟的Cu析出过程的孤立溶质Cu原子浓度的演化曲线，黑色曲线为文献[30]中对应的模拟结果。模拟结果表明，MISA-AKMC模拟结果的曲线和文献[30]中的结果十分相近，两曲线误差在允许范围内。

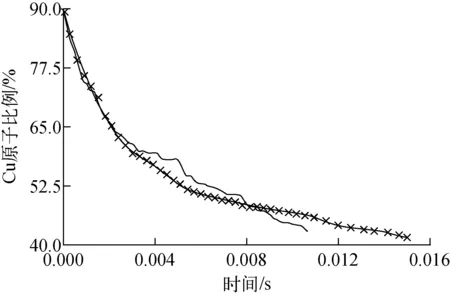
图8 Cu溶质析出过程中的孤立溶质Cu原子比例的演化曲线Fig.8 Evolution of number of isolated solute atoms as a function of time

将模拟过程中的各阶段进行可视化，示于图9。从可视化结果能观察到Cu原子聚集现象，验证了模拟结果的正确性。

图9 MISA-AKMC模拟的Cu溶质析出过程可视化Fig.9 Visualization of Cu solute precipitation simulation

4.3 软件性能测试

为验证并行KMC框架和基于该框架开发的计算模型的性能，进行强扩展性测试。在曙光平台上，采用80×80×80的模拟盒子，其中合金比例为95.98at%Fe-1.34at%Cu。模拟的通信步数为10，通信时间阈值为3.0×10-7s，即总模拟的蒙特卡罗时间固定为3.0×10-6s。

由于MISA-AKMC中采用的事件选择算法时间复杂度为O(N)，N为MPI进程中的缺陷数量。为维持强扩展性测试中的问题总负载不变的要求，需给不同规模的输入算例设置不同的缺陷数。这是因为每个进程上，执行跃迁后的时间增量取决于该进程上的总跃迁速率，而总跃迁速率与进程中缺陷数量和类型等因素有关。假设每个缺陷对应的事件的跃迁速率大致相等，那么容易得到，在保持固定负载的前提下，运行kp个MPI进程时，体系中引入的总缺陷数量应为p进程时的k倍。这里，对于进程数分别为1、2、4、8、16、32时，初始的空位缺陷数量分别为128、256、512、1 024、2 048、4 096。当MPI进程数从1增加到32时，相同负载下的加速比约为8，且运行时间会持续减少，并行具有持续的加速效果，这说明，该算例可强扩展到32倍或更高倍数的进程数量。从MISA-AKMC的并行效率结果(图10)来看，当MPI进程数扩展到基准代32倍时，并行效率从100%降到24%左右，软件并行效率良好。

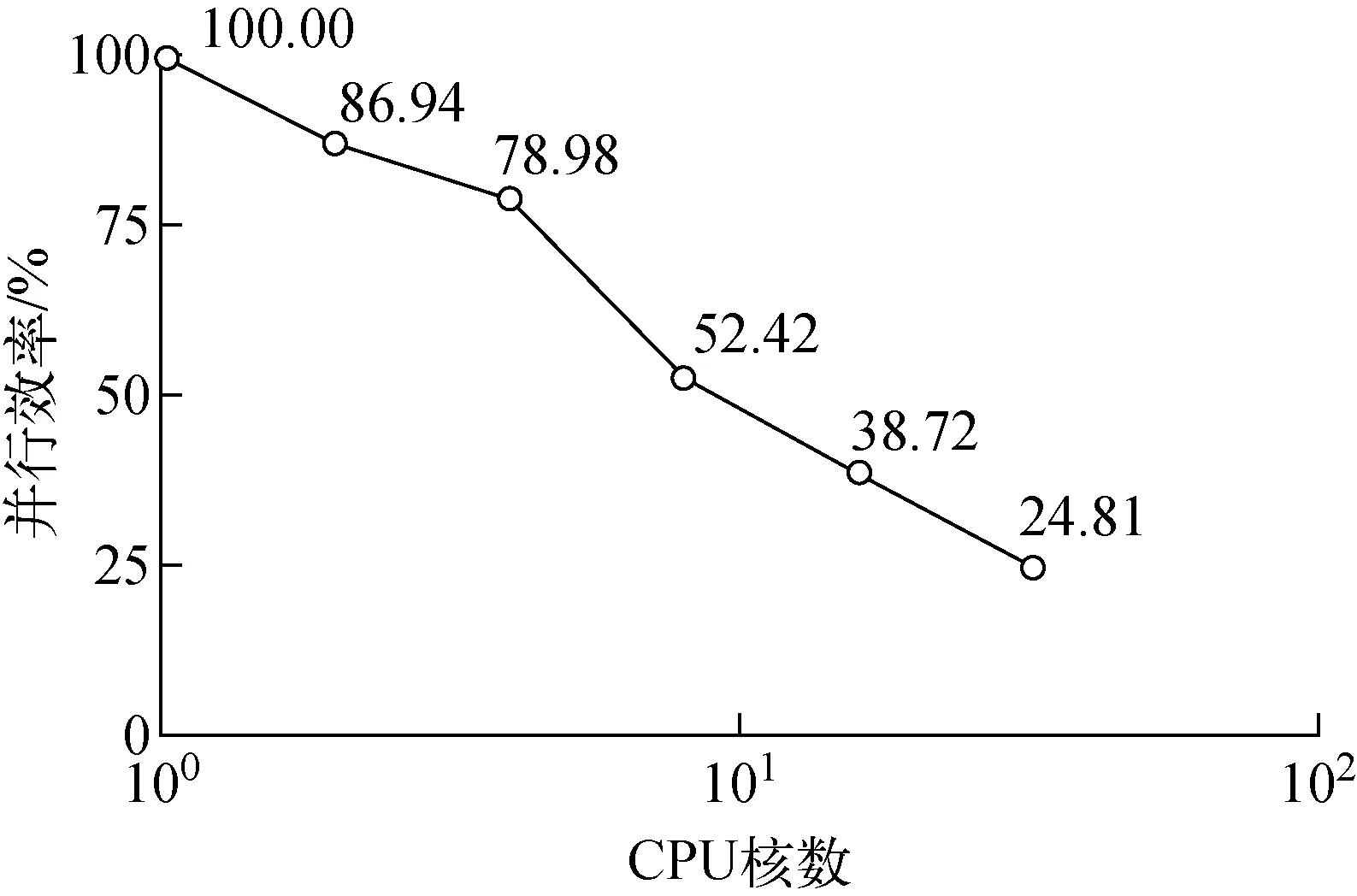
图10 MISA-AKMC并行效率测试结果Fig.10 Result of parallel efficiency test of MISA-AKMC

5 结论和展望

面向材料辐照微观结构演化模拟计算需求，本文基于KMC方法开发了并行KMC框架和用于模拟核材料辐照损伤的并行程序MISA-AKMC，并介绍了其实现细节，包括sub-lattice并行方法、通信策略以及程序优化。通过将MISA-AKMC用于模拟Fe-Cu合金的富Cu团簇析出过程，验证了程序的正确性。在此基础上，进行了程序的强可扩展性测试，从单核扩展到32倍核心，强扩展的并行效率保持在24%以上，性能测试表明MISA-AKMC具有良好的扩展性。

本文涉及的KMC实现代码均在github上开源，可通过http:∥github.com/misa-kmc/misa-akmc获取。针对MISA-AKMC未来的开发，将进一步完善势函数计算，结合机器学习方法引入更高效和更精确的势函数；同时会考虑off-lattice机制，进一步丰富原子尺度材料模拟社区。