数值堆结构力学高精细模拟的并行实现和优化技术

邢龙岳，王昭顺，蒋章程，高付海，高 岳，冯仰德，王 珏

(1.北京科技大学，北京 100083；2.中国原子能科学研究院，北京 102413；3.中国科学院 计算机网络信息中心，北京 100190)

核能作为一种清洁、安全和经济的新型能源，是解决能源危机与环境问题的有效途径，制约核电发展的关键是核反应堆的安全问题。在过去的20年中，欧洲、美国和中国的研究为虚拟反应堆的发展提供了重要信息[1-4]。由于反应堆堆芯组件具有多样性和复杂性，实现全堆高精细结构力学模拟所需的计算资源和存储资源远非服务器和小型集群计算系统所能满足。因此依托高性能计算技术，实现高精细的数值模拟就成了研究反应堆安全性的一条不可或缺的途径。而我国异构体系结构的高性能计算系统目前居世界领先地位，且E级规模(每秒10×1018次数学计算)先进计算系统也即将来临。基于超级计算机和先进建模技术的数值堆(CVR)结构力学模拟是在此背景下诞生的一个挑战性的研究领域。CVR结构力学模拟是研究堆芯组件的静、动态结构变形及应力应变。

异构计算系统中GPU处理器主要可分为NVIDIA GPU和AMD GPU。AMD GPU处理器实现了一种并行微体系结构，不仅为计算机图形应用程序还为通用数据并行应用程序提供了一个极好的平台。大多数需要高带宽和计算密集型或数据密集型应用程序都可在AMD GPU处理器上高效运行[5]。如何对AMD GPU在异构计算系统进行核心优化以获得高性能对程序员来说是一个挑战。高精细模拟采用三维空间有限元分析方法[6]，网格划分是有限元分析的重要环节，是实现高精细数值模拟的基础。对非结构化网格生成的研究，相关学者已进行了数十年，尽管已提出了多种方法[7-8]来提高网格生成的效率，但是对于前沿应用程序的模拟而言，生成大规模网格的时间仍难以接受。本文利用堆芯组件的同构性，通过使用单个组件或局部组件的网格文件自动生成全堆芯网格，从而极大地提高大规模(百亿、千亿级别)网格的划分效率。通过数值模型推导将有限元网格转换为稀疏线性刚度矩阵方程组Ku=r。由于刚度矩阵K具有对称正定的特征，因此可使用大类算法Krylov子空间迭代法[9-10]中的共轭梯度(CG)[11]小类算法，并采用Jacobi[12]预处理进行高效数值求解。

1 CVR全堆芯大规模网格自动生成

CVR全堆芯大规模网格自动生成方法支持有限元分析前处理的完整功能，包括CVR几何建模、有限元分析预处理、大规模并行网格生成3个阶段。图1为CVR全堆芯大规模网格自动生成技术流程图。

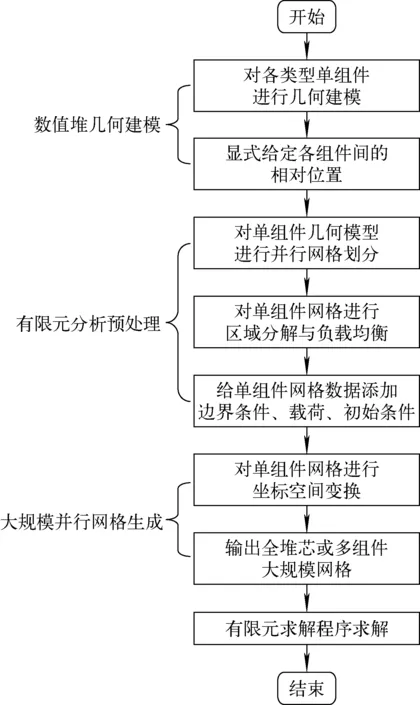
图1 CVR全堆芯大规模网格自动生成技术流程图Fig.1 Flow chart of CVR core large-scale mesh automatic generation technology

1.1 数值堆几何建模

采用反应堆全堆芯结构的标准尺寸，对各类型组件分别进行一次几何建模，并将几何模型的底面中心点坐标设置为(0，0，0)。以中国实验快堆(CEFR)为例，采用常用的CAD模型文件格式(STEP、IGES、Brep、GEO等[13])，分别对其中的燃料组件、乏燃料组件、钢屏蔽组件、硼屏蔽组件、安全棒组件、调节棒组件、补偿棒组件、中子源组件进行几何建模。图2为CEFR全堆芯组件分布，表1列出CEFR全堆芯组件说明。

表1 CEFR全堆芯组件说明Table 1 CEFR whole core assembly description

图2 CEFR全堆芯组件分布Fig.2 CEFR whole core assembly distribution

CEFR全堆芯712根组件的分布方式为多层正六边形阵列，且有1个中心组件，其二维中心点坐标为坐标轴原点(0，0)，相邻组件的中心距为61 mm。对每根组件进行编号后，计算求得每根组件的中心点坐标，并建立组件编号与组件中心点坐标的映射关系。采用上述方法确定CEFR全堆芯712根组件中心点坐标后，根据组件类型对每根组件进行编号。通过输入所需组件的编号集合，即可导出所需的反应堆各类型组件的几何模型文件及几何位置数据。图3为CVR几何建模实现流程。

图3 CVR几何建模实现流程Fig.3 CVR geometric modeling flow chart

1.2 有限元分析预处理

调用三维有限元网格生成器Gmsh[14]，对1.1节中导出的几何模型进行并行网格划分，输出不同类型组件的网格文件。通过自编写的接口程序调用ParMetis/Metis库[15]和Zoltan库[16]，对网格数据进行区域分解与负载均衡处理，划分得到各类型单个组件的多个分区的网格数据，并将所得的网格数据写入不同的网格文件中，用于实现后续有限元求解程序的并行求解。

对各类型组件的网格子文件集添加有限元求解所必需的控制参数包括：边界条件、初始条件、材料属性。其中，边界条件包括位移边界条件和力边界条件；初始条件包括初始位移、初始速度、初始加速度、初始温度和初始状态变量；材料属性包括密度、弹性模量、泊松比和热膨胀系数。图4为有限元分析预处理实现流程。对于相同类型的组件，其材料属性是相同的，但是边界条件和初始条件可能不同，如组件上温度的分布情况。针对这种情况，需进行两次物理参数的添加：第1次是对基准组件网格添加材料属性等恒定不变的物理参数(当组件底面都被固定时，不同组件的位移边界条件也是相同的，因此相关物理参数也可在第1次就进行添加)；第2次是在进行1.3节所述的大规模并行网格生成时，实现不同组件间存在差异的物理参数的自动分配和添加。

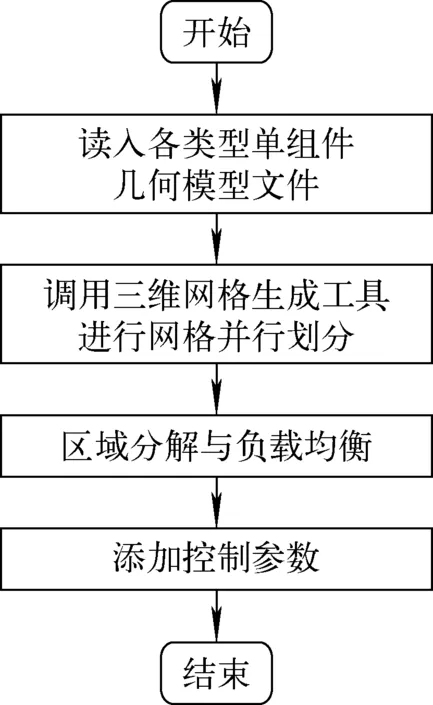
图4 有限元分析预处理实现流程Fig.4 Finite element analysis preprocessing flow chart

1.3 大规模并行网格生成

使用传统的网格划分软件对全堆芯组件进行大规模网格划分，需通过网格生成算法进行节点生成、网格构造、网格排序、网格质量优化等数据操作，常用的网格生成算法时空复杂度列于表2，其中，n为单根组件的网格数量。以百亿网格文件为例，相关网格数据的大小接近1 TB，对计算机的计算能力和存储能力要求极高。目前常用的网格划分工具，最大网格划分速率基本维持在8 000～9 000 s-1。假设划分速率为10 000 s-1，完成百亿网格数量的划分任务需要277.8 h。为了解决这个问题，本文设计并实现了大规模并行网格生成程序。该程序基于同类型组件间具有同构性的特点，不需对所有的组件进行整体网格生成、构造、排序和质量优化，只需对于其中一个基准组件进行网格生成，再通过对基准组件的网格进行网格的复制和平移，即可生成多组件乃至全堆芯组件的网格，大幅减少与网格生成相关的大量运算。同类型组件间网格的坐标空间变换方式有平移、旋转、镜像等(图5)。

图5 同类型组件网格几何变换示意图Fig.5 Geometric transformation of the same type assembly mesh

表2 常用网格生成算法的时空复杂度Table 2 Time and space complexity of common mesh generation algorithm

针对全堆芯组件进行大规模网格生成，分别采用组件间网格串行生成方法、组件间网格并行生成方法及本文提出的大规模网格并行生成(组件间网格并行复制)算法，各自所需的时空复杂度列于表3。其中，m为堆芯中所需生成网格的组件数量。可看出，组件间网格并行复制方法的时空复杂度是最优的。

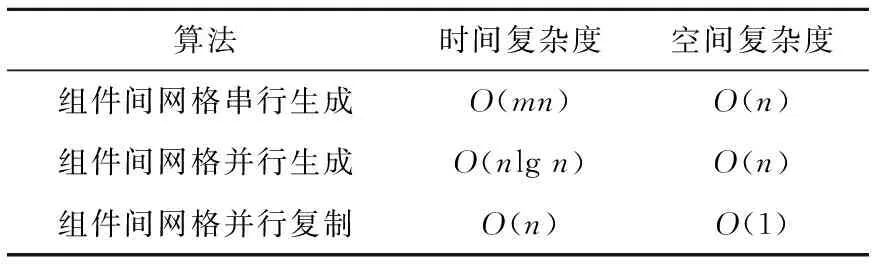
表3 组件间网格生成算法的时空复杂度Table 3 Time and space complexity of mesh generation algorithm between components

网格数据主要包括网格节点数据、网格单元数据和控制参数。网格节点数据用于说明每个网格节点的坐标；网格单元数据用于说明每个网格单元由哪些网格节点构成；控制参数用于说明影响问题求解的各参数选项。得到添加了控制参数(包括物理参数、与求解相关的参数、计算结果输出路径等)的网格子文件集后，通过大规模并行网格生成程序读取单个组件的网格子文件集及几何位置数据，并进行网格节点坐标的移动、转换，网格节点及网格单元编号的变换，由于不同组件的控制参数可能存在差异，因此还需进行相关控制参数的变换，输出所需的CEFR全堆芯或多组件的网格数据[17]。其中，在进行控制参数的变换前，需在脚本文件中按不同组件的编号写入不同组件间具有差异性的控制参数，在进行网格复制转换的同时，程序会将不同参数分配给指定的组件，即进行第2次物理参数的添加。

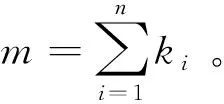
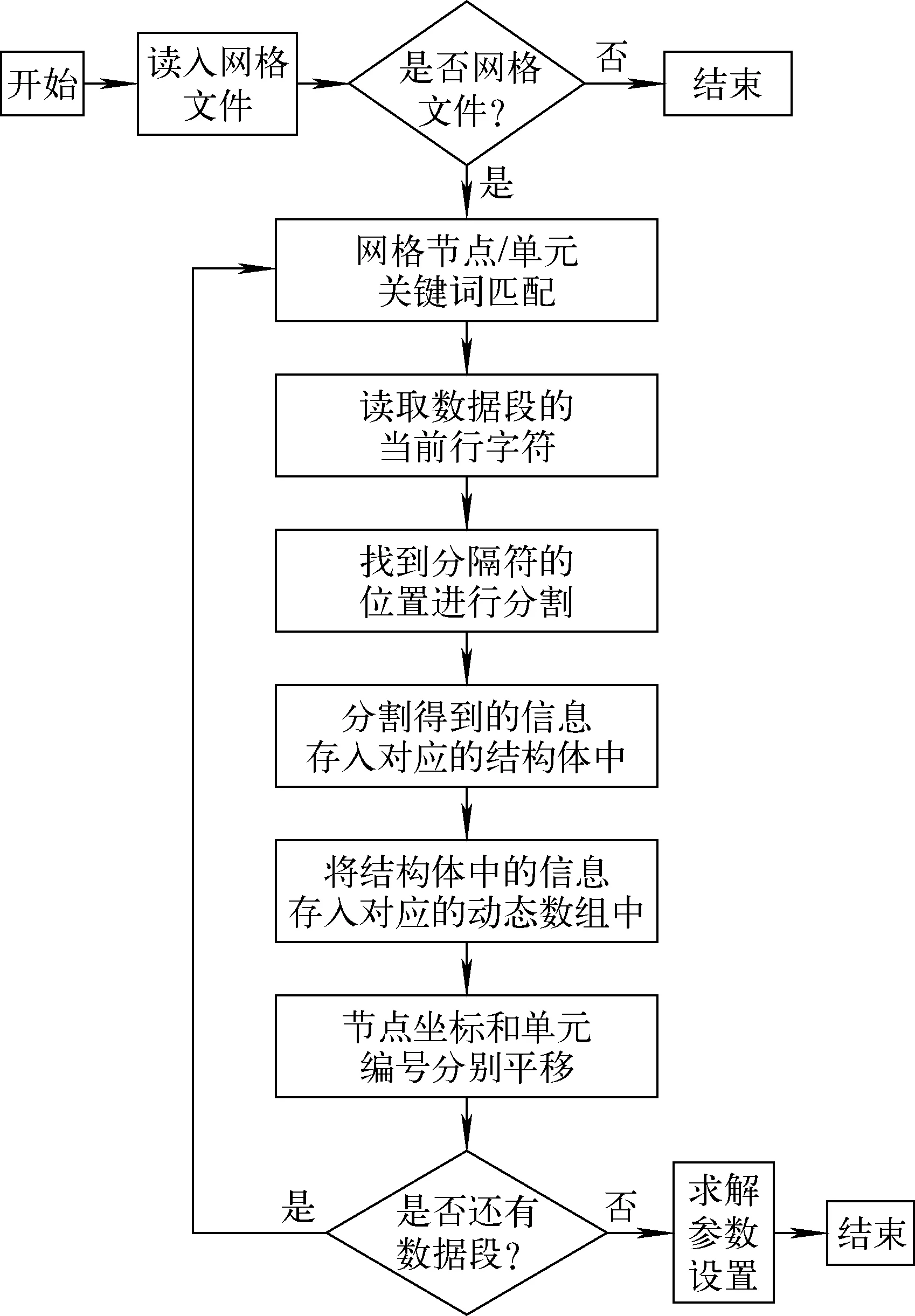
图6 大规模并行网格生成程序流程Fig.6 Large-scale parallel mesh generator flow chart

2 大规模稀疏刚度矩阵线性方程组并行求解算法设计

本文采用ANSYS对简单立方体静力算例的用时估算(图7)，可得出百亿网格量的求解用时将近116 d。另外，由于在大规模计算中系数矩阵过于庞大，采用Jacobi预处理的方法进行加速。但随着每个并行区域中刚度矩阵的规模逐渐增加，预处理的迭代次数会明显增加，收敛速度变得十分缓慢。这不但增加了每个计算核心所处理的浮点计算量(FLOPs)，而且增加了更多的计算核心资源使用，导致产生大量的通信时间。

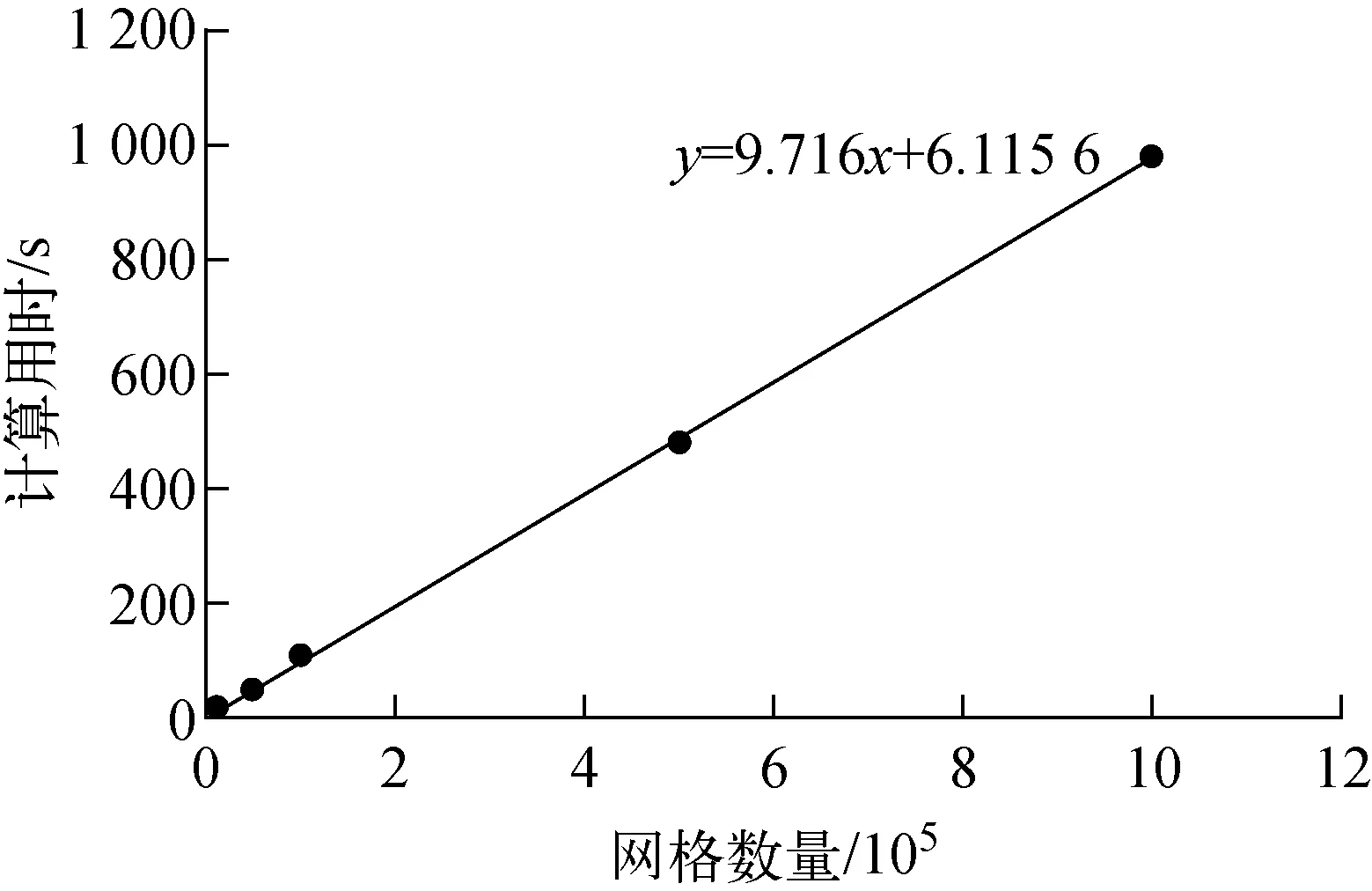
图7 ANSYS立方体静力算例用时Fig.7 Time for ANSYS to solve cube static example

2.1 异构平台上的并行计算

GPU提供了一种拥有强大浮点计算能力和极高存储器带宽的低成本、低功耗通用的CPU+GPU异构计算平台[18-19]。其特点可支持高度并行、多线程并拥有众核处理器。以天河2号超级计算机Intel(R) Xeon(R) CPU E5-2692v2为例，单CPU双精度浮点计算能力为211.2 GFLOPs，数据传输能力为50～60 GB/s，而单AMD GPU(Vega series)双精度浮点计算能力则可达到6.25 TFLOPs，是前者的28倍以上，且与显存之间的传输最高可达1 TB/s。

CPU和GPU浮点计算能力差异显著的原因是因为GPU是专门为图形渲染而设计的，而图形渲染计算特点为计算密集型、高并行度计算。因此GPU更致力于数据处理而不是数据缓存和流量控制，为了达到高密度计算的要求，GPU芯片上有更多的算术逻辑单元。CPU与GPU结构的差别如图8所示。具体来说，GPU更适合解决大规模并行计算的问题，即适用于同一程序同时对多组具有较高计算密度的数据进行运算。因为同样的程序代码在每个数据元素上执行时，对精密流量控制的要求较低，尤其适合大规模稀疏刚度矩阵向量乘。

图8 CPU与GPU结构的差别Fig.8 Difference between CPU and GPU structures

2.2 并行方案

在包含AMD GPU的异构计算系统中，并行计算过程中允许使用大量Thread。可根据并行编程模型为每个数据或数据集设置一个Thread，并以AMD GPU中每个计算单元中可执行的最大Thread数量来划分，从而获得最优的并行计算性能。为此需对实际的应用特征进行分析并给出方案。

1) 密集内存访问

CEFR静力数值模型构造的稀疏刚度矩阵线性方程组Ku=r在多个计算节点间并行计算时，各计算单元需要将内存中的数据读入到显存，并将计算的结果写入到内存。并行规模越大，这种访存操作所消耗的时间将会大大超过计算所消耗的时间，因此在大规模计算时，访存的时间开销将成为提高计算效率的最大瓶颈。解决此类问题，可采用内存与显存之间的数据分块和双缓冲技术，以减少访存的时间。

2) 同步要求

计算规模越大，迭代次数就会越多，这是Jacobi迭代法特质决定的。在Jacobi迭代中，除第一次计算外，每次迭代需各计算单元同步并更新上一次迭代的数据，这需要AMD GPU结束内部所有线程才能实现全局同步。为了减少同步开销，首先要减少迭代次数，可采用分块Jacobi方法，这种方法对刚度矩阵的构造是有要求的，因此需在预处理组装刚度矩阵时进行额外的处理。该方法能大幅减少计算的迭代次数；其次只为每个MPI进程分配1个块，这样可有效减少主机端与设备端额外的数据传输，并均衡各进程间的负载，降低对同步的时间开销。

在求解Ku=r时，每个计算单元之间数据是相互依赖的，同一个单指令多数据(SIMD)单元执行的线程在所有的计算节点中会寻址连续的内存块，因此将每个进程中的向量计算数据连续存储，这样相邻线程执行时只需对上一个线程的数据索引加1就可得到当前线程的向量计算数据，从而提高计算性能。

2.3 AMD GPU中的并行优化设计

有限元方法得出的结果是近似值，因此要实现反应堆堆芯结构力学高精细模拟，则网格量需达到十分庞大的规模，这也将生成巨大的Ku=r方程组，所以面向AMD GPU，本文基于Krylov子空间迭代法，提出了几种并行优化设计。

1) HIP编程模型中的线程部署

在AMD GPU上编程的语言称为HIP，它构建了可迁移的运行时体系结构，这个体系结构允许HIP程序可动态地在多个平台进行切换。HIP是显式编程模型，需要在程序中写出详细的并行控制语句，包括数据传输、核函数的启动等。所谓核函数Kernel就是运行在AMD GPU上的函数。在CPU上运行部分称为主机端(host，执行管理+启动)，在AMD GPU上运行部分为设备端(device，执行计算)。程序流程是在主机端串行执行，当到设备端执行时则首先将需计算的数据通过hipMemcpy传递给AMD GPU(即将CPU存储中的内容传递给AMD GPU的显存)，然后调用核函数启动函数hipLaunchKernelGGL使AMD GPU开始计算，Kernel端计算完成后再用hipMemcpy将计算的数据从AMD GPU拷贝回CPU。其中hipMemcpy是阻塞的，数据拷贝后才可进行后面的程序，hipLaunchKernelGGL是非阻塞的，执行后程序继续往后执行，但在Kernel未计算完成之前，最后一个hipMemcpy不会开始。

在HIP中对设备端Kernel使用三级并行编程模型对其并行化进行线程部署，如图9所示。按照3D布局部署Grid、Block和Thread，以平衡每个矩阵维度上计算域的分解。相邻的Block共享位于边界上的数据，且Block中的每个Thread负责在每次迭代中更新数据，而Threads实际是以Wavefront执行的，为实现最优并行化，映射时将Block中的Thread数量设置为Wavefront执行数的倍数，这样可达到更好的计算效果。

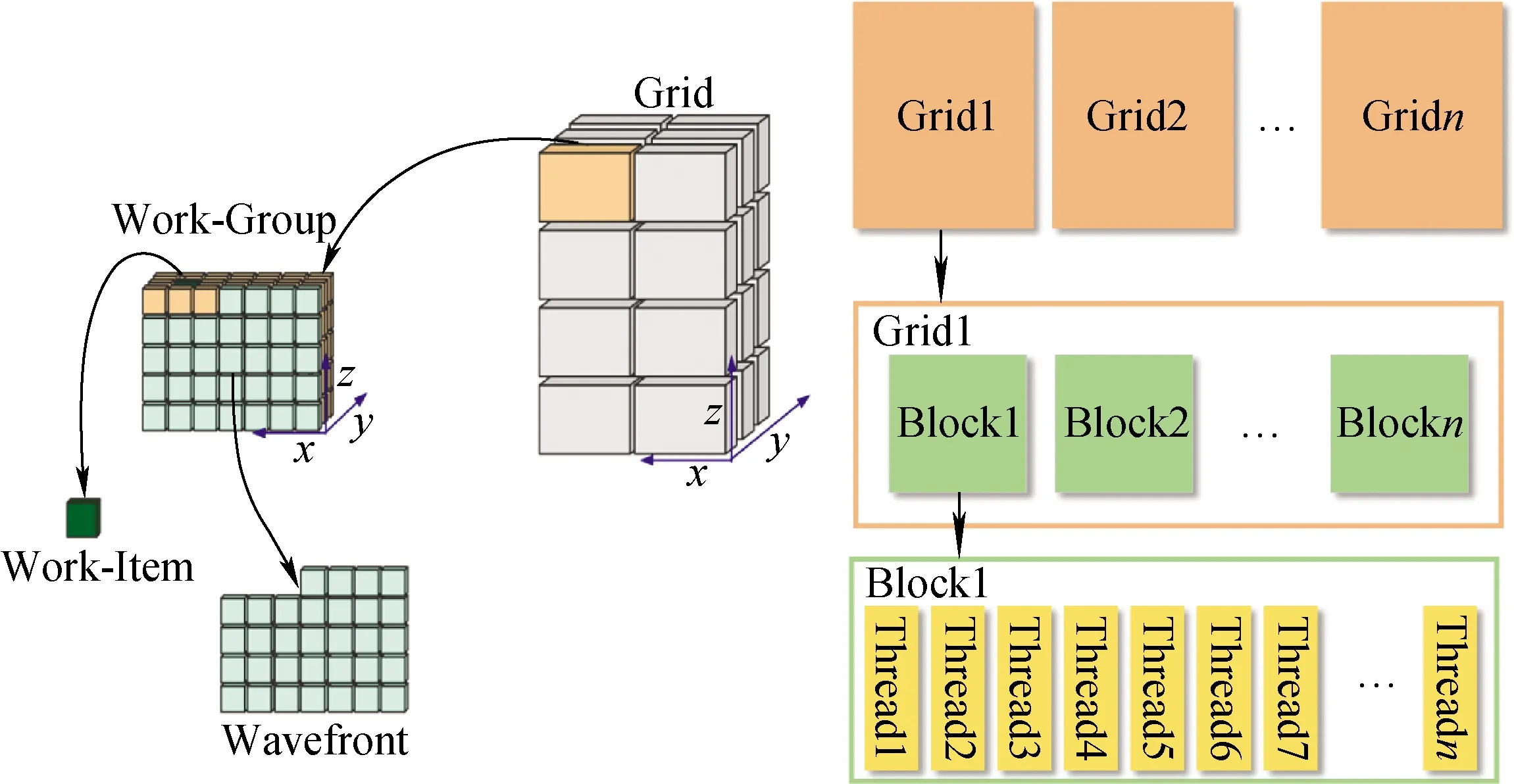
图9 并行化策略的线程部署Fig.9 Thread deployment of parallelization strategy

2) 数据预取

在执行核函数时，主机端计算是阻塞的，数据拷贝完成后才可进行后面的程序。若多个核函数同时执行则需很大的时间开销。若将一个核函数放入一个逻辑队列中，多个向量计算分别建立多个核函数，就可在AMD GPU中采用流水线并行实现数据预取，如图10所示。这种方案可充分利用CPU与AMD GPU的计算资源，提高计算效率。

提素质、强能力，创新人才工作新机制。一直以来西南铜业公司党委匡正选人用人风气，完善选人用人机制，坚持严管和厚爱结合、激励和约束并重，优化干部考核评价机制。抓好各级干部的领导、监管、属地和执行责任，提升党政共融，党务干部要抓安全、懂生产、谋经营，行政干部要讲政治、会党建、抓文化。完善激励机制和容错纠错机制。开展好选人用人制度修订、培训及考核、中层管理人员画像、后备干部选拔等工作。坚持党管人才原则，推进员工人才成长体系建设，明晰各条人才通道的晋升、考核、退出、流动机制，为培养公司“素质优良、结构合理、队伍稳定”的员工队伍打下扎实基础。

图10 流水线并行中的数据预取Fig.10 Data prefetching in pipeline parallel

3) 数据对齐

在对齐的边界上创建数据可提高CPU上的SIMD性能。若向量数据未与缓存线大小对齐，编译器必须额外处理未从缓存线边界开始的数据部分的计算，从而导致性能损失。因此，需根据向量寄存器上缓存线的大小来设置动态分配的数据对齐字节数，图11为512位向量寄存器上的数据未对齐。

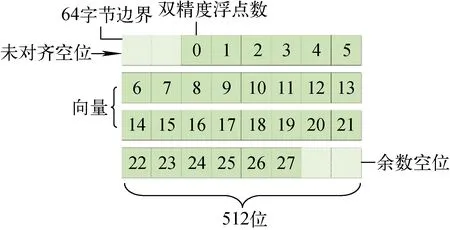
图11 512位向量寄存器上的数据未对齐Fig.11 Data alignment on 512 bites vector register

3 性能与验证

3.1 测试算例与测试目标

对CEFR堆芯组件与全堆芯组件进行百亿网格划分和形变位移的测试，测试算例边界载荷为下过度接口处铰支，约束所有平动自由度，燃料组件添加温度载荷的变化区间为300～500 ℃。表4列出了CEFR堆芯燃料组件物理参数设置。测试目标包括：1) 采用这种方法的可行性和正确性，通过国际原子能机构(IAEA)标准例题的解析解进行对比；2) 采用这种方法后对反应堆结构力学大规模并行模拟的加速效果的提升；3) 多节点集群上优化程序的并行可扩展性。

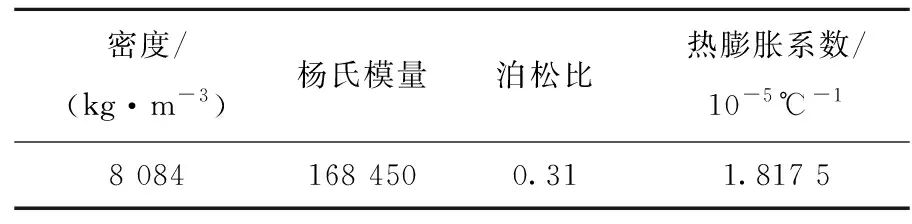
表4 CEFR堆芯燃料组件物理参数设置Table 4 Physical parameter setting of CEFR core fuel assembly

3.2 AMD GPU的加速性能

将CEFR单燃料组件划分为1 947 584个有限元网格，通过有限元力学数值模型将其转化为稀疏刚度矩阵线性方程组的形式Ku=r，然后使用Krylov子空间迭代法中的CG方法和Jacobi预处理，结合在AMD GPU中的并行方法对其进行计算。CPU计算核心从1个CPU Core扩展到32个，并使用1～4个AMD GPU与之结合。实验结果展示了在其并行算法下使用AMD GPU对计算性能的加速效果。图12为单燃料组件形变位移分布和CPU+AMD GPU加速效果，可看出，当1个节点中使用4个CPU Core和4个AMD GPU时，并行计算效率最高，而在32个CPU Core和4个AMD GPU的计算中执行时间最短，但并行强可扩展性不佳。

图12 单燃料组件形变位移分布(a)和CPU+AMD GPU加速效果(b)Fig.12 Deformation displacement distribution of single fuel assembly (a) and CPU+ADM GPU acceleration (b)

3.3 功能与规模测试

1) CEFR全堆芯百亿网格划分

首先分别为燃料组件、乏燃料组件、硼屏蔽组件、事故棒组件建立CAD几何模型；然后针对不同类型组件划分并生成单组件网格文件；再将各种类型组件之间的相对位置信息写入配置文件；最后自动生成全堆芯大规模网格文件。CEFR全堆芯百亿网格生成实现流程如图13所示。

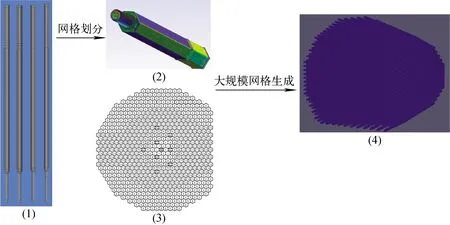
图13 CEFR全堆芯百亿网格生成Fig.13 CEFR whole core 10 billion meshes generation

反应堆全堆芯大规模网格自动生成方法还可将生成后的网格均匀地划分为多个网格区域，以8组件为1组的网格区域分解与负载均衡效果如图14所示，其中不同的色块代表不同的划分区域。将单组件划分到1 432万网格，每根组件可划分96个分区，可实现102亿的全堆芯网格量，且最高可划分137亿，数据存储量为1.067 TB，网格数据由节点位置数据和点、线、面、体几何模型数据组合而成，包含坐标(double)、编号ID(int)、类型ID(int)、物理ID(int)、点ID(int)。全堆芯网格文件以二进制文件存储，网格文件数量等同于分区数量，并可转换为vtk格式使用Paraview可视化。

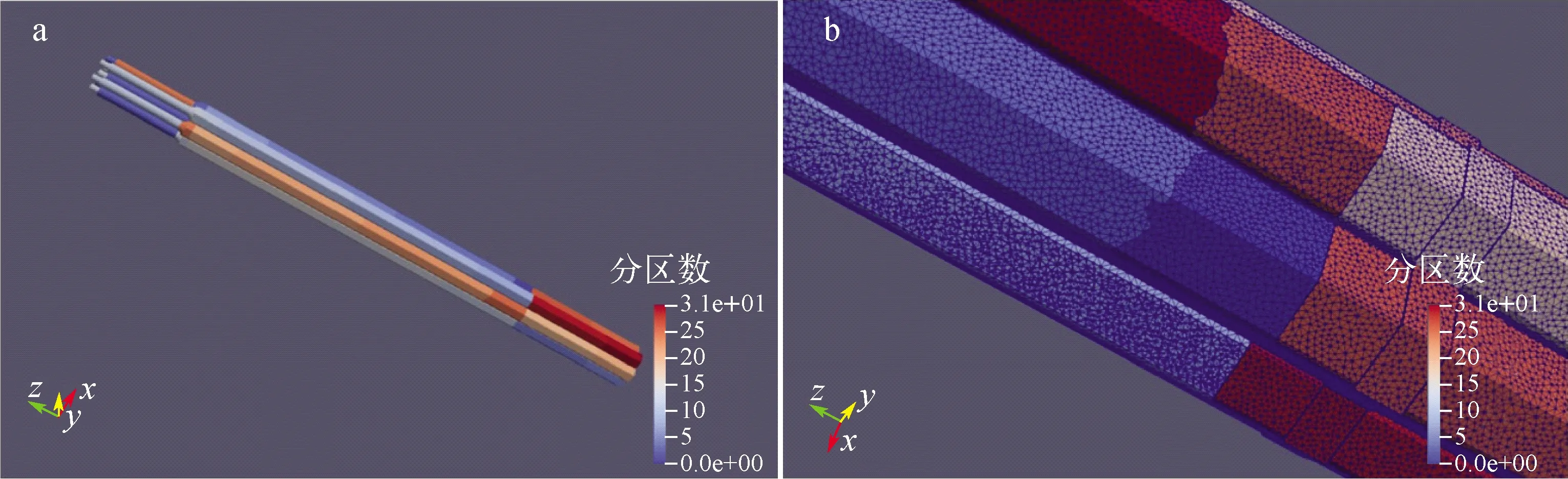
图14 网格区域分解(a)与负载均衡(b)Fig.14 Mesh domain decomposition (a) and load balancing (b)

2) CEFR全堆芯大规模静力分析

首先采用六角形套管单组件的静力学热形变位移计算模型，与IAEA标准例题的解析解对比，验证静力学计算结果的正确性(表5)。

表5 IAEA标准例题静力学验证算例Table 5 Static verification example of IAEA standard example

通过对程序计算结果和理论值的对比，分别给出了六角形套管单组件在给定线性温度梯度下弯曲变形量(表6)和轴向伸长量(表7)在高度为4 000、3 000和2 500 mm处的偏差情况。组件弯曲变形量和轴向伸长量的数值解与理论值偏差较小，验证了计算结果的正确性，可视化效果如图15所示。

图15 六角形套管单组件弯曲变形量(a)和轴向伸长量(b)模拟结果Fig.15 Simulation result of bending deformation displacement (a) and axial elongation (b) of single hexagon casing assembly

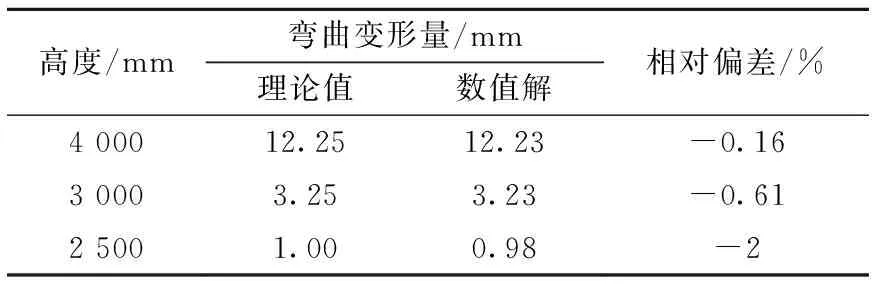
表6 六角形套管单组件在给定线性温度梯度下的弯曲变形量Table 6 Bending deformation of single hexagon casing assembly under given linear temperature gradient

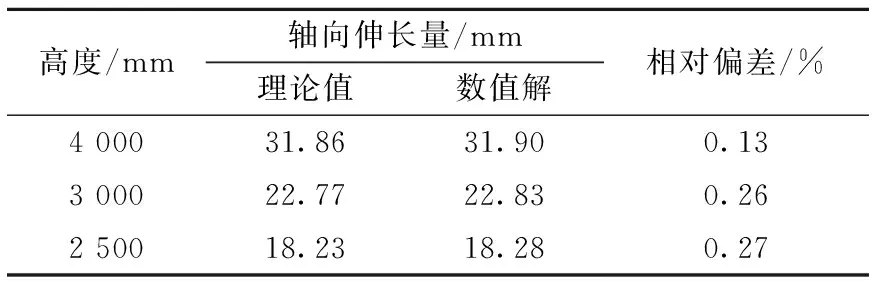
表7 六角形套管单组件在给定线性温度梯度下的轴向伸长量Table 7 Axial elongation of single hexagon casing assembly under given linear temperature gradient

结合异构计算系统的AMD GPU，对整个CEFR全堆芯组件划分为0.54～102亿网格的计算模型进行静力分析模拟，算例列于表8，静力模拟结果的形变位移分布如图16所示。

表8 CEFR全堆芯组件的静力学算例Table 8 Static example of CEFR whole core assembly

图16 CEFR全堆芯形变位移分布Fig.16 Deformation displacement distribution of CEFR whole core

对具有0.54亿网格量的CEFR全堆芯组件计算模型进行静力模拟，计算节点从64个节点扩展到512个节点，每个节点使用258个计算核心，最高使用到132 096个。CPU+AMD GPU加速比与效率对比和并行弱可扩展性如图17所示。在异构AMD GPU计算系统上与CPU的版本相比，提高了30%以上的计算性能。另外，以9 504计算核心(CPU+AMD GPU)对应1.584亿网格量为基准扩展至615 168计算核心对应102.528亿网格量，测试出并行弱可扩展性达到53%。

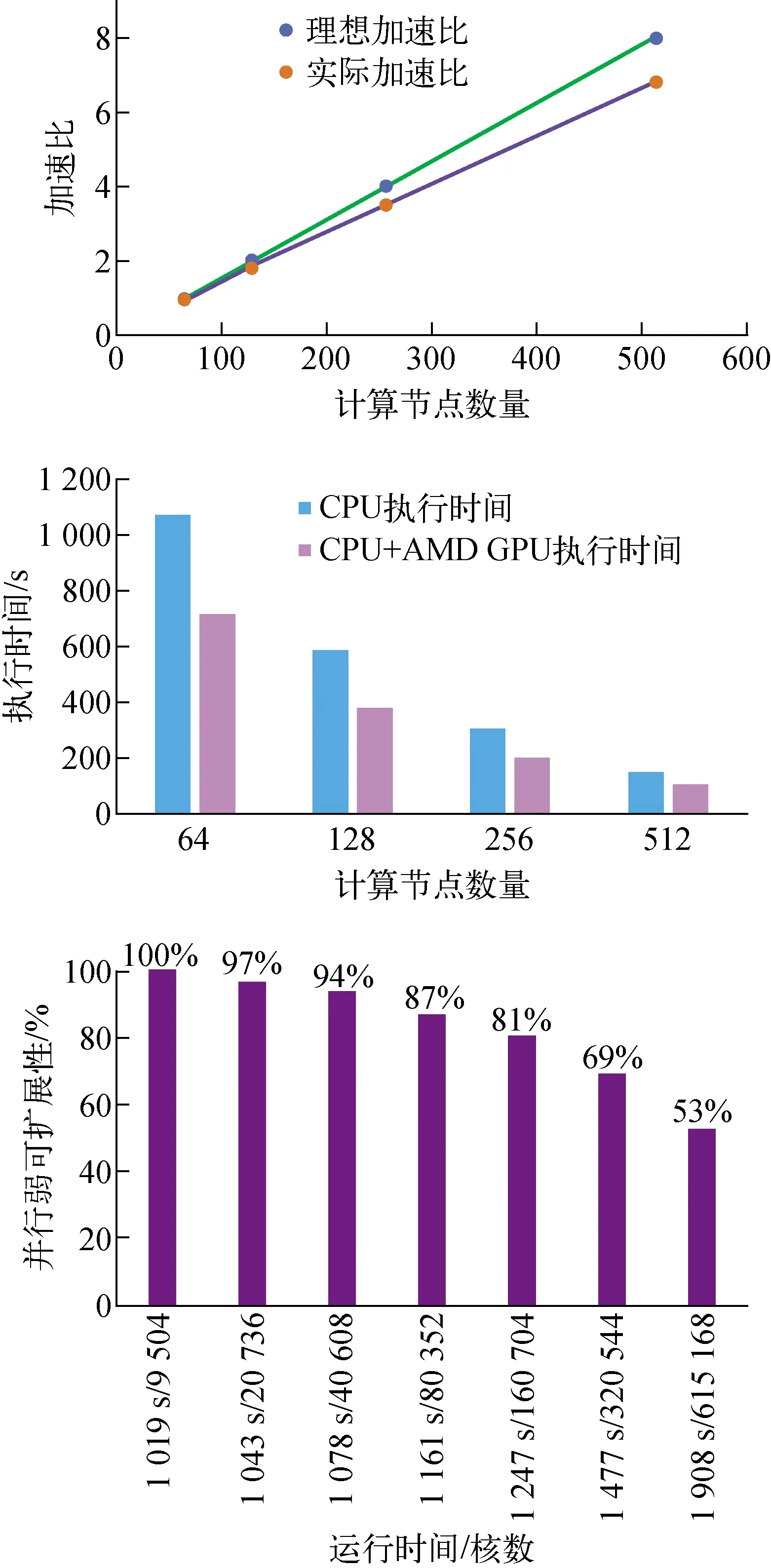
图17 CPU+AMD GPU加速比与效率对比和并行弱可扩展性Fig.17 CPU+AMD GPU speedup, efficiency and parallel weak scalability

4 结论

本文利用CEFR堆芯组件的同构性，通过使用单个组件或局部组件的网格文件自动生成全堆芯大规模网格，从而解决了传统方法受计算机内存资源、网格文件大小的限制而导致的大规模网格划分难以实现的问题。包括网格划分功能在内，本文提供了有限元分析前处理的完整功能，使得生成的全堆芯网格文件能直接作为有限元求解软件的输入文件。

基于AMD GPU体系结构，研究了CEFR堆芯数值模型构造的稀疏刚度矩阵线性方程组Ku=r的并行计算。采用适合于对称正定刚度矩阵K的Krylov子空间迭代法的CG法求解并使用Jacobi预处理加速。结合AMD GPU体系结构，采用数据预取和数据对齐的并行优化方法，在AMD GPU体系结构计算系统上，通过对CEFR单组件和全堆芯组件的模拟计算，大规模稀疏刚度线性方程组Ku=r的计算效率得到了显著的提高。另外，在数据并行性方面，根据AMD GPU体系结构的特点优化了内存访问和数据布局。