基于DPM模型的某型号水轮机固定导叶泥沙磨损模拟与实验研究

司 序，曾永忠，刘小兵

(西华大学流体及动力机械教育部重点实验室，四川 成都 610039)

0 引 言

我国河流泥沙含量较高，水轮机磨损及磨损带来的安全隐患、效率下降、检修频繁以及供电不稳定是难以避免的，水力机械的泥沙磨损一直是国内外学者研究的重点。本文为了提高夏特水电站水轮机机组的运行效率以及运行稳定性，针对其水轮机固定导叶进行了数值模拟，并与实验结果对比，验证了离散颗粒模型，即DPM模型(Discrete Phase Model)对水轮机固定导叶磨损模拟的有效性。

近年来，国内外很多学者基于DPM模型对各种水力机械进行了研究，得到了大量的研究结论：钟功祥等[1]基于DPM冲蚀预测模型研究了部分井场在地面采用一种新型的高压管汇快接装置的冲蚀磨损问题；Hashemisohi等[2]采用稠密离散相模型结合颗粒流动力学理论和实验结合的方法，研究了多组分颗粒混合物在流化床中的鼓泡特性和分离；陈作炳等[3]以立磨整机为研究对象，运用实验和模拟结合的方法，用离散相模型DPM的双向耦合计算方法求解颗粒运动轨迹，从速度、压强以及离散相分布方面分析了立磨流场两相流的相互耦合作用以及颗粒分级筛选特性。在水轮机磨损的数值模拟和实验研究方面，廖姣等[4]对某混流式水轮机进行全流道数值模拟，分析不同工况下转轮叶片表面泥沙分布和固液两相速度，为该电站水轮机的改造提供了理论依据；张惠忠等[5]对夏特水电站水轮机进行了数值模拟和并对其关键过流部件进行了泥沙磨损试验，预估了水轮机的泥沙磨损情况，为夏特水电站水轮机的抗磨设计和运行提供了重要参考依据。

1 数学模型

在欧拉-拉格朗日双流体模型中，颗粒被视为离散相，连续相和离散相是相互渗透共存的连续介质。本文采用k-ε模型模拟液体湍流流动，假设内流场中只有清水相(连续相)和泥沙相(离散相)，且两相的物理性质均稳定不变，离散相为圆形，采用颗粒动力学方法模拟离散相流动过程，数值模拟了某型号水轮机固定导叶工作时的流动特性。在两相流动计算时，先在欧拉坐标系下求解清水相，即连续相的控制方程，待计算收敛后，再将离散相颗粒注入流场；然后在拉格朗日坐标系下求解离散相的微分方程，从而得到离散相颗粒的流动特性。

1.1 连续相控制方程

因为相间没有质量转移，连续相的质量守恒方程和动量平衡方程描述为[6-7]

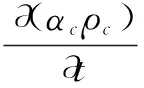
(1)

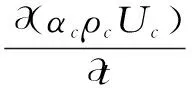
(2)

式中，αc为连续相的相分数；ρc为连续相的密度；UC为连续相的平均速度；RC代表应力张量；p为平均压力；g为重力加速度矢量；A为动量界面交换项。

1.2 离散相控制方程

离散相在流场运动过程中，主要受到曳力、重力、浮力及离散相间的碰撞力，由于固相在液相中重力、浮力及离散相间的碰撞力与曳力数量级不同，故而我们在研究时主要考虑曳力，忽略其他几个力[2，4]。由于离散相模型既不考虑离散相间的碰撞，也不考虑离散相本身的体积大小，因此离散相运动微分方程形式如下

(3)

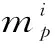
1.3 磨损模型

我们所采用的的DPM模型中的磨损通用模型如下[7-9]

(4)

式中，C(dp)为离散相直径函数；a为离散相与壁面的冲击角；v为离散相速度；b(v)为相对速度函数；f(a)为冲击角函数。

(5)

2 水轮机固定导叶的泥沙磨损特性分析

2.1 水轮机固定导叶的建模及网格

本文以某型号水轮机固定导叶为研究对象，根据水轮机的设计参数和运行范围，在模型综合曲线图上选取工况点进行全流场模拟分析。提取出一个单流道，根据相似原则将叶片长度缩小至0.2倍，将原本的流线设计为某型号水轮机固定导叶的壁面，在其中放置导叶，如图1所示。再将流场的几何条件、物性条件、边界条件、初始条件等都遵循相似原理，近似模拟某型号水轮机固定导叶流场。

图1 流道设计示意

使用ICEM对提取出的模型进行非结构化网格的划分，其首层网格高度为0.01 mm，对叶片前缘、尾缘处进行局部网格加密，选用出口流量为网格无关性检测的参考标准，最终确认的网格数为2 754 518，如图2所示。

图2 网格示意

运用商业CFD(Computational Fluid Dynamics)软件ANSYS(FLUENT)中的离散相模块对流场进行模拟，其主要设置如下：首先选用标准k-ε模型作为湍流模型；其次在在离散相模块设置中启用磨损模型；然后在入口处增添注射器模块(Injection)，主要用于确定固相颗粒的粒径、初始速度、质量流量等参数。进口边界条件为速度进口，其速度为6.53 m/s；假设离散相与连续相的速度相同，离散相由进口面进入流场，离散相的质量流量为2.11 kg/s；出口边界条件为压力出口，大小是一个标准大气压101 325 Pa。离散相完全逃逸，湍流强度为5%，粒径为0.0001 m，壁面条件为无滑移壁面，颗粒与壁面完全弹性碰撞，在近壁面采取标准壁面函数，冲击角函数考虑到准确性使用了5段分段线性设置，其速度指数函数为常数2.6。

2.2 水轮机固定导叶泥沙磨损数值计算结果

图3为水轮机固定导叶工作面和背面的磨损率云图，图4为固定导叶1/2叶高处的泥沙浓度和速度的变化规律。在本研究中，由于离散相直径假设为常数，故冲击角、流速和叶片每个位置的颗粒浓度为影响磨损率最大的原因。因考虑到边壁效应，本文研究对象为湍流的充分发展区，即固定导叶在1/2叶高处的变化规律，其结果如图4所示，虽0.6倍～0.9倍弦长的位置速度较高，但泥沙浓度很低；又由图3可以看出，0.6倍～0.9倍弦长的位置磨损率仍然较高。我们认为这是因为这部分的冲击角度和动能较大，泥沙颗粒在惯性的影响下，冲破边界层的高压区，撞击到壁面。泥沙浓度在叶片每个位置虽有不同但在同一条弦长上的变化不大，认为对同一弦长的位置，磨损率受冲击角度和绕流速度的影响最大。

图3 固定导叶磨损率云图

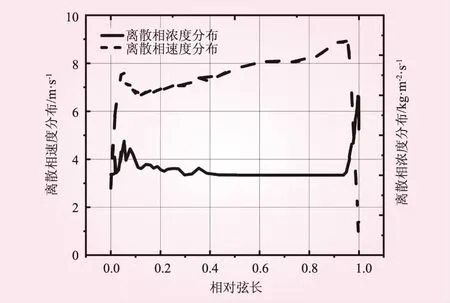
图4 固定导叶背面离散相的浓度和速度与弦长的关系

3 水轮机固定导叶的泥沙磨损特性实验

实验台由动力系统、冷却系统、泥沙水混合系统组成。本实验的动力系统最大动力630 kW，实验中用水泵冲击搅拌实现对泥沙的均匀混合，再用蛇形管抽取地下水进行冷却。试验段针对某型号水轮机固定导叶，依据上述方法设计试验段流道，流道装置如图5～6所示。

图5 导叶试件装置实物

图6 导叶流场实验流道装置

为了使工作环境与某型号水轮机固定导叶工作环境相同(包括流量、流速、压力、流道、含沙量等)，采用电站提供的沙样，含沙量为该电站最大含沙量9.52 kg/m3，固定导叶材料为Q345R，其边界条件与数值模拟完全相同。

实验后，通过白光干涉轮廓仪来读取试件表面磨损深度。白光干涉轮廓仪是一种高效的、非接触式磨损测试设备，测量精度为0.1 nm，其原理是通过干涉条纹，来比较样品测试表面跟理想参考面的偏差。通过显微镜物镜的垂直扫描测试样品表面，得到整个扫描区域的三维数据测试结果及表面深度信息，再比较磨损前后信息，得到试件的磨损量。

4 模拟与实验结果的对比分析

为了避免流道壁面边界层的影响，实验图和模拟图的磨损量均取自1/2叶高处，固定导叶磨损率模拟数据和实验数值的对比见图7。由图7可知，实验结果与模拟结果的磨损率趋势大致相同。但实验中，泥沙颗粒不全是圆形，直径也不全是0.1 mm，因为离散相的升力、粘性阻力、BASSET力均受到离散相体积当量直径的影响，同时在模拟时，球形颗粒表面光滑，与壁面发生碰撞时，只有摩擦磨损这一种磨损方式，而实际中有摩擦磨损和切削磨损2种磨损方式，所以实验中的磨损量和模拟结果相近却又不完全相同。

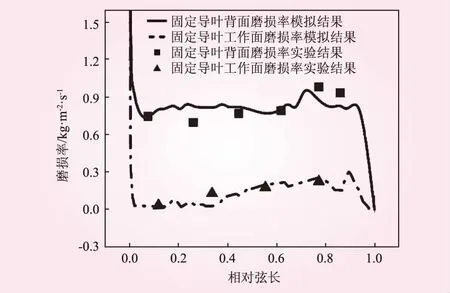
图7 固定导叶磨损率模拟数据和实验数值的对比

由图7可知，0.3倍～0.5倍弦长的位置磨损率极低，这是因为这个位置的离散相受到曳力影响较大，径向速度小，其受惯性力影响小，不易克服二次流和边界层内的高压区阻力，离散相与壁面碰撞时的动能也变得很小，故而磨损率较小。随着弦长的增大，冲击角和壁面的角度不断变化，冲击角不断变大，速度越来越大，在0.9倍弦长的位置达到最大值，所以离散相获得的用来克服二次流和边界层高压区阻力的动能越多；同时随着冲击角度的改变，径向速度也越来越大，泥沙浓度也在这个位置开始增大，在这几个因素的作用下，离散相对壁面的冲击作用越强，壁面的磨损率随之逐渐增大。由壁面的磨损率的公式(4)常用函数可知，磨损率随绕流速度泥沙浓度的增加而增加，随冲击角的增大而增大，与模拟结果和实验结果吻合。

5 结 论

(1)通过数值模拟得到了某型号水轮机固定导叶在设计工况下的磨损分布规律，为夏特电站水轮机机组固定导叶部件的日常维护间隔周期提供了参考。

(2)验证了该水轮机固定导叶磨损率与水流的绕流速度和泥沙浓度的关系基本符合磨损公式。

(3)基于DPM模型，对某型号水轮机固定导叶进行了两相流动模拟，得到了固定导叶的磨损率和速度分布情况，与实验结果基本吻合，验证了DPM模型对水轮机过流部件磨损模拟的有效性。