纤维定向布放钢纤维混凝土力学性能及断裂过程细观分析

王辉明，朱 文，贺正波

(1.新疆大学建筑工程学院，新疆 乌鲁木齐 830046;2.新疆建筑结构与抗震重点实验室，新疆 乌鲁木齐 830046)

0 引 言

钢纤维混凝土(Steel Fiber Reinforced Concrete，SFRC)作为一种纤维增强水泥基复合材料在工程中已得到广泛应用，已有研究发现只需加入1%～2%的钢纤维就可使SFRC抗拉强度和抗弯强度分别提升40%～80%和60%～120%[1]。在混凝土路面、管道工程、机场跑道、桥梁、铁路等主要承受拉应力结构(梁板类构件)中，由于结构底部长期处于受拉状态，因此抗弯性能已被作为评价工程质量的重要指标[2-5]。对于按一般施工工艺制作的SFRC，其中的钢纤维分布位置随机、排列方向杂乱，钢纤维方向与构件主拉应力方向往往不一致，造成大量钢纤维没有充分发挥其抗拉作用，考虑到钢纤维与砂浆界面容易形成薄弱层进一步消减了钢纤维增强效率，因此实际发挥效能可能更低。随着施工技术的进步，当前已提出一些在水泥基体硬化过程中控制钢纤维方向的有效措施，如利用自密实混凝土的流动性使钢纤维定向，还有通过磁场装置对钢纤维进行磁化定向，幕儒等[6- 8]设计并申报了制备定向钢纤维增强水泥基复合材料(Aligned Steel Fiber Reinforced Cementitious Composites，ASFRC)的专利，实现了钢纤维方向系数达0.9以上的定向布放钢纤维混凝土制备，为最大限度发挥钢纤维的增强增韧效率提供了技术手段。

当前在定向布放钢纤维水泥基复合材料方面的研究已取得一些成果。卿龙邦等[9]采用扩展有限元法，研究了不同钢纤维掺量下ASFRC的单轴抗拉强度，其数值模拟的力-位移曲线与试验结果拟合良好，并得出结论，ASFRC较SFRC可有效提高抗拉强度；李辉等[10]对ASFRC试块进行了相关力学性能试验，试验结果表明ASFRC的抗弯性能和抗拉性能都优于SFRC，且表现了更好的延性。考虑到钢纤维混凝土中的粗骨料随机分布等因素导致数量众多的钢纤维统一定向较为困难，因此定向布放钢纤维混凝土试件制作难度较大，试验测试工况极为有限，导致目前对于ASFRC构件断裂过程以及定向钢纤维的阻裂增韧机理研究尚不充分。本文基于实际试验配合比随机生成二维钢纤维混凝土梁细观模型，其中体积分数相同的钢纤维采用随机乱向分布、受拉区水平定向布放和沿最大主拉应力布放3种方式，结合黏结裂缝模型，对钢纤维混凝土梁抗弯实验进行数值模拟，分析钢纤维掺量和取向对钢纤维混凝土的力学性能影响，将数值计算结果与已有试验结果进行对比分析，可有效避免试件制作的困难，细观层次的数值模拟可以更好的分析定向布放钢纤维混凝土损伤破坏过程及钢纤维阻裂机理，有助于对ASFRC断裂行为和相关力学性能展开更深入的研究，为工程设计和应用提供理论依据和参考。

1 细观有限元模型建立

根据均匀化理论，复合材料的宏观力学性能，如弹性模量主要取决于夹杂(粗骨料)形状的主轴方向和体积分数。当复合材料中夹杂主轴方向随机均匀分布时，夹杂形状对宏观力学性能的影响较小，为了尽可能接近真实情况，本文粗骨料形状采用凸多边形。考虑到计算效率，本文细观模型为二维混凝土梁，其尺寸为400 mm×100 mm；参考实际试验[11]，骨料级配为粒径5～15 mm二级配混凝土，混凝土级配见表1。钢纤维形状为端钩型，直径为0.8 mm，长径比为60。钢纤维掺量分别为0.5%、1%、1.5%、2%。

表1 混凝土配合比

1.1 骨料数的确定

研究发现混凝土按照富勒(Fuller)级配公式可以得到较为理想的密实度和强度，因此本文按照Fuller公式确定粗骨料各粒径对应的体积分数，其表达式为

(1)

式中，d为筛孔直径；P为骨料通过筛孔直径的累积百分通过率；dmax为最大粒径。利用瓦拉文(Walaraven)公式根据体积分数换算出二维情况下的颗粒粒径及颗粒数见表2。

表2 二级配混凝土等效粒径及颗粒数

1.2 模型生成

为了保证钢纤维能均匀地分布在混凝土中，各项组分材料投放顺序为先投放钢纤维，再投放中骨料，最后投放小骨料。对于钢纤维随机乱向分布和受拉区水平定向分布的ASFRC，钢纤维和骨料的位置坐标用蒙特卡洛方法生成。对于沿最大主拉应力定向布放的ASFRC，钢纤维的布放需要先用连线近似画法绘制最大主应力迹线，再使钢纤维沿着最大主应力迹线布放，最后用蒙特卡罗方法生成骨料。生成的二维钢纤维混凝土梁细观模型如图1所示。

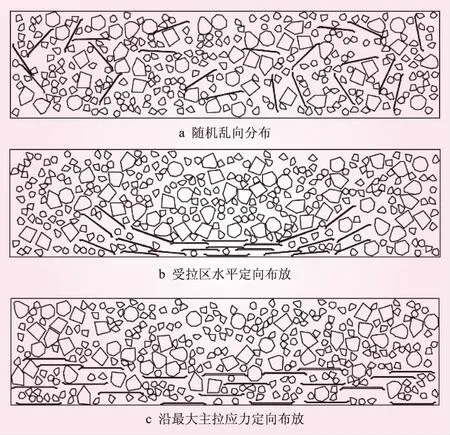
图1 掺量为1.5%的钢纤维混凝土梁细观模型

1.3 本构关系及破坏准则

裂纹的产生和发展是混凝土结构损伤破坏过程的主要特征，在细观尺度下混凝土破坏的根本原因是内部微裂纹的萌生和扩展，用黏结单元模型模拟裂纹扩展已经广泛应用于混凝土开裂过程分析[12]。本文研究工作中在砂浆-砂浆、砂浆-骨料、砂浆-钢纤维之间嵌入零厚度黏结单元，其本构关系由牵引分离定律确定[13]。黏结单元上作用有法向牵引力Tn和切向牵引力Tt，牵引力随着裂缝面的法向分离位移δn和切向分离位移δt的增大而减小，应力─位移关系采用线性软化关系，如图2所示。

图2 线性软化黏结单元本构关系

牵引分离定律相关参数包括Ι型断裂能Gnf、法向黏结强度Tn0、法向完全分离位移δnf；、II型断裂能Gtf、切向黏结强度Tt0、切向完全分离位移δtf。起裂法向位移δn0和起裂切向位移δt0。当牵引力达到黏结强度时刚度开始退化，需要注意的是只有拉伸和剪切情况下导致刚度退化，压缩情况刚度则不变[14]。

(1)损伤起始准则。损伤起始准则用于判断何时开始损伤、刚度开始衰减。本文采用的是最大名义应力损伤起始准则，损伤开始时满足

(2)

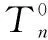
(2)损伤演化准则。损伤演化准则用于表达在下降段分离位移和牵引力如何发展，黏结单元损伤演化可表示为

(3)

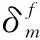
(4)

式中，<δn>表示压缩时为0，拉伸时为δn。由式(3)可知，D的取值范围为0～1，0表示未损伤，1表示完全损伤。损伤产生后黏结单元的法向刚度和切向刚度分别衰减为

kt=(1-D)kt0

(5)

kn=(1-D)kn0

(6)

式中，kn0、kt0分别为初始法向刚度，和和初始切向刚度。

2 细观模型验证

选取文献[11]中钢纤维随机乱向分布的SFRC四点弯曲试验进行验证。梁中部两点加集中力，两边支座同时约束竖向位移，一边支座约束水平位移。实际加载方式采用位移加载，加载及约束位置如图3所示。

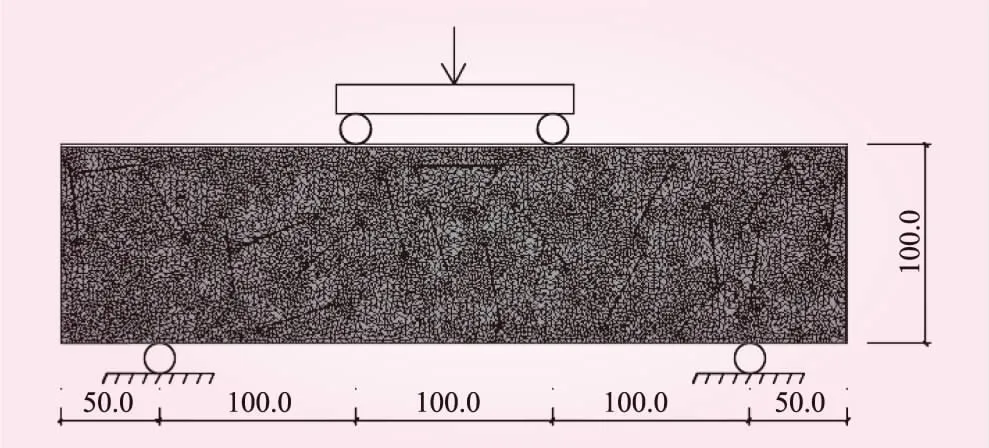
图3 四点弯曲试验有限元模型(单位：mm)

本文采用ABAQUS程序进行有限元分析，粗骨料、钢纤维、砂浆基质采用平面应力单元CPS3，黏结单元采用COH2D4单元。各项组分材料参数[15]见表3。

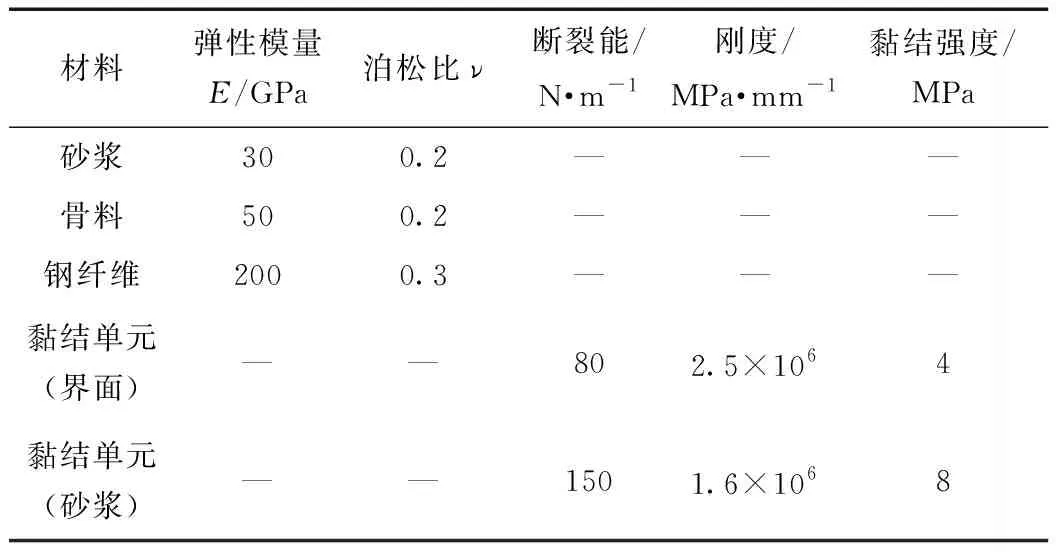
表3 材料参数

数值模拟过程中最先在骨料和砂浆之间的界面层出现裂纹，随着荷载的增大，砂浆内部也出现微裂纹，荷载再增加这些裂纹相连形成一条贯通裂纹，且加载位置和支座附近的混凝土也已压碎，此时已表明构件处于破坏状态。钢纤维掺量1.5%的SFRC梁四点弯曲试验破坏形态见图4，实际试验试件破坏图像见图5，可见数值模拟破坏现象与试验破坏现象相符。

图4 四点弯曲试验破坏过程

图5 试验试件破坏图像

数值计算得到的不同掺量下SFRC梁四点弯曲抗弯强度与试验测试结果比较如图6所示，可见两者吻合较好，说明本文的细观有限元模型具有足够的可靠性。

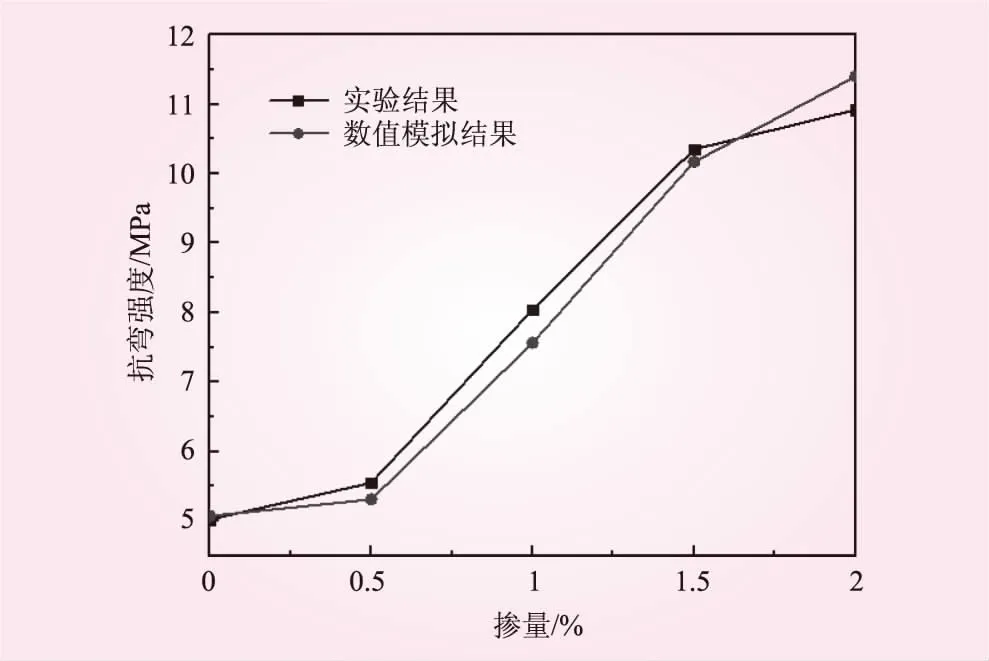
图6 SFRC梁抗弯强度比较3ASFRC梁抗弯试验数值模拟

3 ASFRC梁抗弯试验数值模拟

3.1 ASFRC四点弯曲试验

由于施工较难，ASFRC中钢纤维通常为在混凝土内部全截面水平定向。为进一步探索ASFRC增强增韧机理，本文研究考察ASFRC中钢纤维受拉区水平定向布放和沿最大主拉应力方向定向布放2种工况。梁尺寸、钢纤维掺量、加载及约束情况均与前述SFRC梁相同，采用位移加载方式。对2种模型进行数值计算，得出不同掺量下梁的抗弯强度，四点弯曲试验抗弯强度如图7所示。

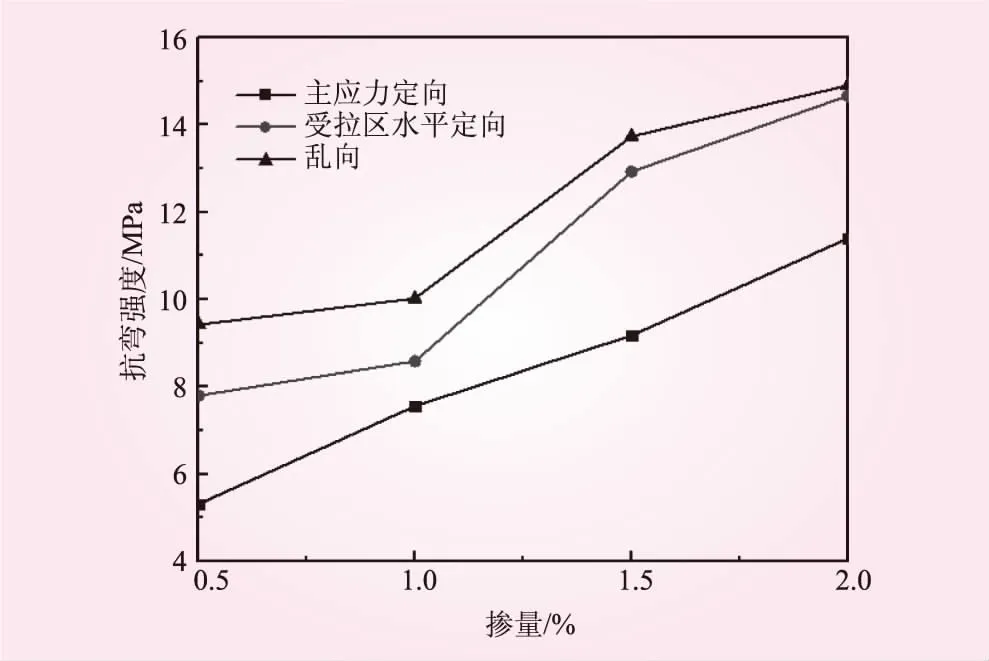
图7 ASFRC梁四点弯曲试验抗弯强度

由图7可知，无论钢纤维是水平定向布放还是沿主拉应力方向定向布放，都比随机乱向分布所承受的抗弯强度大，且都随着掺量增加而增大；其中受拉区水平定向可以提高抗弯强度13.5%～46.89%，沿最大拉主应力定向可以大幅提高抗弯强度30.79%～77.4%。而沿最大主应力定向布放与受拉区水平布放相比抗弯强度相近，大约提高了1.64%～20.8%。这也进一步证明了钢纤维取向越与最大主应力方向一致，抗弯强度提升也越高。图8为钢纤维掺量为1%时四点弯曲试验梁的破坏形态。

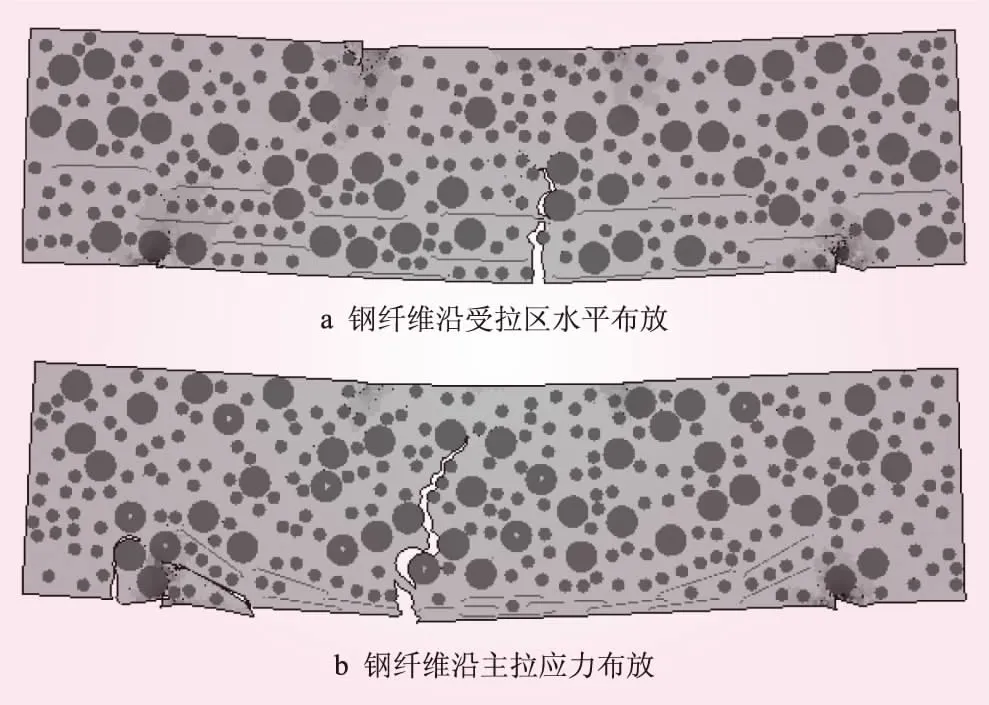
图8 ASFRC梁四点弯曲试验破坏形态

为了验证钢纤维定向布放对混凝土延性提高水平，本文还提取了3种工况(乱向分布、受拉区水平定向、最大主应力定向)下达到破坏强度时的跨中挠度，并绘制了挠度-掺量曲线，如图9所示。

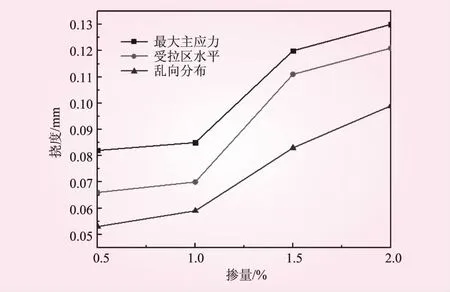
图9 四点弯曲挠度-掺量关系曲线

从梁的损伤破坏过程中发现，由于梁底受到最大主应力(拉应力)最大，往往跨中梁底部位先破坏[20]。梁底钢纤维沿最大主应力布放，由于钢纤维的桥接作用致使裂纹的扩展必须绕过钢纤维而耗散更多能量，达到阻裂的效果；构件中的钢纤维可将混凝土中的拉应力转移到了抗拉强度高的钢纤维上，改变了构件内应力状态分布，提高了构件的韧性，且构件韧性随钢纤维掺量增加而增加。其中，钢纤维沿最大主应力布放可提高31.31%～57.72%，受拉区水平布放可提高18.64%～33.73%，而沿最大主应力定向布放较受拉区水平布放相比韧性大约提高了7.44%～24.24%。

3.2 ASFRC三点弯曲试验

工程中梁构件跨中受集中力作用，即三点弯曲也是常遇到的情况，本文对三点弯曲进行了分析，三点弯曲数值模拟方法及过程均与上文四点弯曲相同，所得抗弯强度和破坏时跨中挠度-纤维掺量关系分别如图10、11所示。由图10、11可知，无论三点弯曲还是四点弯曲，钢纤维定向布放都可不同程度提高SFRC强度和韧性，由此可表明钢纤维定向布放可以更好发挥出钢纤维作用，从而提高梁整体强度。

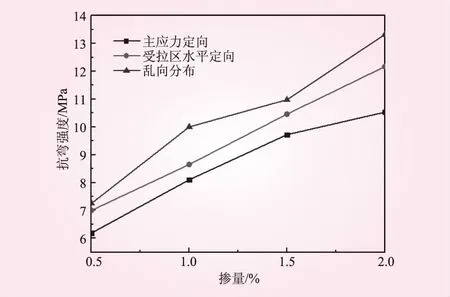
图10 ASFRC梁三点弯曲试验抗弯强度

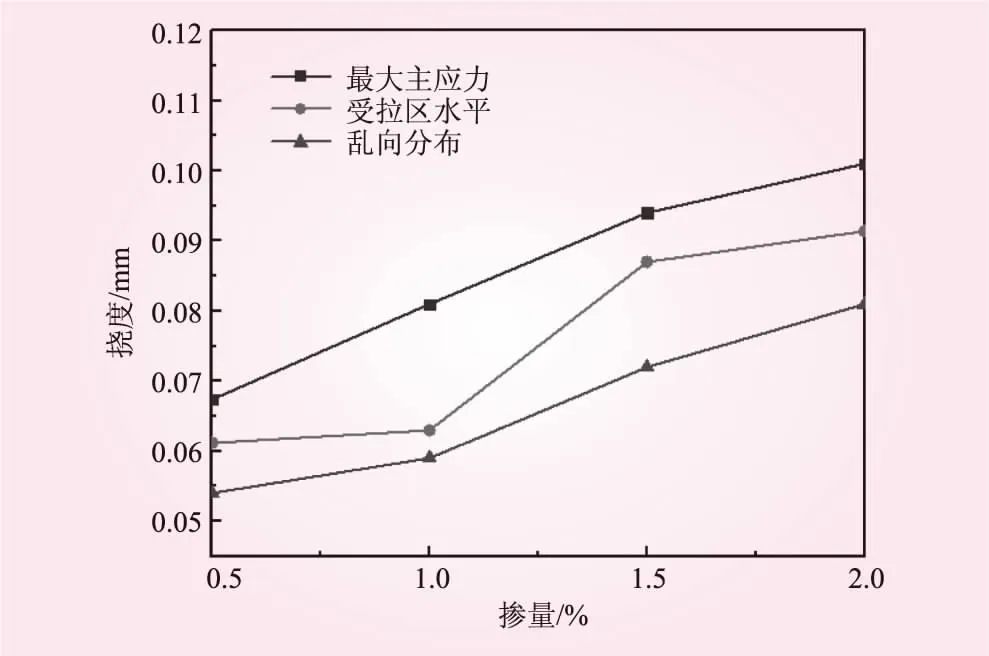
图11 三点弯曲挠度-掺量关系

4 结 论

(1)基于黏结裂缝钢纤维混凝土模拟的四点弯曲强度与试验结果吻合较好，改变钢纤维分布形式可有效提升混凝土力学性能，其中受拉区水平定向布置抗弯强度可提高13.5%～46.89%，沿最大主应力方向布置钢纤维抗弯强度可提高30.79%～77.4%。

(2)钢纤维定向布放不仅可以提高混凝土力学性能，还可以提高混凝土中的应力分布和混凝土构件韧性。其中，受拉区水平定向布放韧性可提高18.64%～33.73%；沿主应力方向布置钢纤维可提高强度31.31%～57.72%。因此钢纤维定向投放可充分提高钢纤维阻裂效果，减缓了混凝土裂纹的产生和发展。