基于数值预报和多方法集成的精细化站点预报技术研究

王 雪，何晓凤，孙逸涵，刘善峰

(1.华风气象传媒集团有限责任公司，北京 100081；2.北京玖天气象科技有限公司，北京 100081；3.北京华新天力能源气象科技中心，北京 100081；4.国网河南省电力公司电力科学研究院，郑州 450052)

引 言

随着数值预报的快速发展，数值预报的分辨率明显提高，但由于其空间分辨率有限，难以对更小区域作出精准气象预测。基于原始数值预报产品的精细化预报，一般有2种方法：一种是通过修改模式提升输出产品的分辨率，另一种是利用降尺度技术[1-2]。方法1对模式改进的要求高，且无法无限制地改进模式输出产品的分辨率；方法2计算量小，模式改进成本低，且可将预报产品插值到更精细的区域或点位，在专业气象服务中发挥了重要作用[3-4]。

降尺度方法包括统计降尺度、动力降尺度及统计—动力相结合降尺度共3种[5]。Wilby等[6-8]对降尺度技术的应用进行了详细阐述。Kidson and Thompson(1998)[9]分别利用统计降尺度和动力降尺度方法进行预测，发现动力降尺度虽有更好的物理基础作为支撑，但统计降尺度简单灵活，其效果与动力降尺度方法的差异不大，从应用角度来看更为可取[10]。

统计降尺度方法是利用原始格点预报产品获取具体区域或点位高分辨率产品的重要途径，常应用于精细化预报[11-12]。在短期天气预测应用领域使用的降尺度方法有双线性插值、反距离权重法、最近邻点插值等空间插值方法[13-18]，此外还有学者使用简单的转换函数[19-21]。

李刚等[20]利用反距离权重插值法对贵州省气象站进行气温精细化预报研究发现，降尺度技术处理后的气温预报效果得以明显改进。吴建秋等[22]采用线性回归和卡尔曼滤波相结合的方法对南京进行温度预报研究发现，降尺度方法有效提高了温度预报的准确度及稳定性。范丽军等[23]利用降尺度方法对华北地区气象站进行月平均温度变化预报研究发现，统计降尺度方法处理后的温度与观测的温度基本一致。

虽然，降尺度方法在一定程度上提高了数值模式产品的精细化预报水平，但多以数学统计为基础，预报过程中没有考虑地形的作用，也无法保证哪种方法永远效果最佳，且目前基于多降尺度方法动态集成技术尚未在精细化预报中得以应用。

本文以河南省气象站为研究对象，基于“最近邻点法、反距离权重法、地形高度最接近法、地形复杂度最接近法”4种降尺度方法及3种集成方法(滚动样本时间分别为1天、3天及7天)，利用2018年四个季节的数值预报产品及站点观测资料，对风速、温度、湿度进行预报效果检验，探讨7种方法对不同季节、不同地貌特征条件下的气象站预报效果。此外，为了充分探索上述方法的普遍性，以大风过程为着眼点，研究大风过程条件下7种方法的站点风速预报能力。

1 数据来源和处理

本文研究区域为32°-36°N、110°-116°E(河南省大部)，使用的数据资料为2018年春(4月)、夏(7月)、秋(10月)、冬(1月)的逐小时模式预报资料及观测资料。

1.1 模式预报数据

GDFS(Grid Data Forecast System)[24]是一套多模式集成预报系统，可输出风速、温度等多种气象要素，以ECMWF(European Centre for Medium-Range Weather Forecasts)和GRAPES_Meso(Global/Regional Assimilation and Prediction Enhanced System)模式产品为输入数据，通过对全国6万多个自动站观测资料与预报资料误差的动态估算，确定不同空间位置、不同预报时刻的集成权重，输出集成预报结果。ECMWF是欧洲中心的高分辨率全球业务模式，GRAPES_Meso[25]是我国自主研发的业务化区域数值模式。

1.2 观测数据

本文从全国气象要素观测的逐时数据集中搜集整理了河南省121个气象站的观测资料，包括风速、温度、湿度等要素。依据地貌特征,将气象站分为A、B、C三类。其中，A类站点海拔高度小于100 m，共70个；B类站点海拔高度范围为[100 m,300 m)，共36个；C类站点海拔高度大于等于300 m，共15个。

2 方法介绍

2.1 4种降尺度方法

2.1.1 最近邻点法

最近邻点法又叫泰森多边形方法，利用插值点最近的单点进行插值，一个隐含假设条件是任一网格点的属性值都使用距它最近位置点的属性值，即采用每一个网格节点的最邻点值作为它的节点值。

2.1.2 反距离权重法

反距离权重法是假设周围样本对预测点均有一定影响，且影响随着距离的增大而减小。本文中反距离权重法采用的周围样本数为4点，其原理是插值点的属性值为周围4点属性值的加权平均，权重系数的大小与插值点到周围4点的距离有关。

2.1.3 地形高度最接近法

地形高度最接近法是考虑了地形高度的一种降尺度方法。气象站是带海拔高度的空间坐标点，预报格点数据是带有空间坐标关系的格子，每个格子均有预报信息，计算插值点与所在预报格点4个节点的海拔高度差，选择高度差最小的节点预报值代表插值点的预报值。

2.1.4 地形复杂度最接近法

地形复杂度最接近法是考虑了地形复杂度的一种降尺度方法。地形复杂度是评价地表崎岖程度的指标，表征地表形态的复杂程度。鉴于本文研究区域处于内陆，定义地形复杂度为：以插值点为中心，划定边长为模式资料分辨率(2.5 km)的正方形区域，搜索此方形区域中真实海拔高度的最高点A与最低点B，即区域中海拔高度相差最大的两个点，然后计算A、B点的海拔高度差值，即为该插值点的地形复杂度γ。地形复杂度的计算采用美国SRTM3的90 m分辨率地形数据，分别计算插值点与所在数值预报网格点4个点位的地形复杂度，选择与插值点复杂度最接近的节点预报值来代表插值点的预报值。

2.2 动态集成方法

本文设置了3种动态集成方法。集成方法中预报值为4种降尺度方法预报值的加权平均，权重的大小与4种方法的绝对误差有关。滚动样本分别为1天、3天及7天，当前时次的权重计算利用历史时次的检验参数(绝对误差)，1天、3天、7天的集成方法中权重计算分别利用前1天、3天、7天检验参数的平均值。此集成方法除考虑了与预报准确性密切相关的距离、地形高度、地形复杂度等要素的指示意义外，还考虑了合理设置4种降尺度方法的权重，可在一定程度上弥补单一降尺度方法的不稳定性和不确定性。公式如下：

AEk,j=|Yk,j-Oj|

(1)

(2)

(3)

式中，Yj为集成方法第j时次的预报值，Oj为第j时次的观测值，Yk,j为第k种方法在第j时次的预报值,Wk,j为第k种方法第j时次的权重，AEk,j为第k种方法在第j时次的绝对误差。

2.3 验证方法

本文采用绝对误差(公式1)评估7种方法的预报性能，绝对误差在一定程度上避免出现正负相抵消的情况，能较好地反映预报效果的实际情况。

3 结果分析

考虑到集成方法滚动样本最长为7天，因此每月的有效检验时段为23天。下文分别是整体评估角度下四个季节三类气象站的风速、温度、湿度分别通过7种降尺度方法处理后的检验情况，以及大风过程下7种方法对风速预报的检验情况。

3.1 整体预报性能评估

3.1.1 风速预报结果分析

分析7种方法处理后的风速相同时刻平均误差的逐时演变发现，季节变化对风速预报影响较小，四个季节的检验结论基本一致(以秋季为例，其余季节图略)：对于地势平坦的A类站点(图1a)，7种方法的平均风速误差差异较小，滚动样本最短的集成方法与反距离权重法的预报误差相对偏低，另外两种集成方法的次之；随着地形高度的提升(图1b、c)，最近邻点法、地形高度最接近法与地形复杂度最接近法的预报效果明显变差，7种方法的预报误差差异明显增大，此时反距离权重法的预报效果最好，滚动样本最短的集成方法的次之，之后是另外两种集成方法的预报效果。分析7种方法在三类站点四个季节的风速日平均误差发现(图略)，四个季节三类站点风速日平均误差的检验结果与逐时风速平均误差的检验结果基本一致。

图1 2018年10月7种方法在三类气象站的风速逐时平均误差

鉴于3种集成方法中绝大部分情况下第一种集成方法预报效果较好，因此采用第一种集成方法与4种降尺度方法进行预报效果对比。对于海拔高度较低的A类站点，5种方法的误差差异较小，B类与C类站点的最值误差的逐时演变基本一致。以B类站点为例(图略)，对比5种方法处理后的风速误差最值发现，经过集成方法处理后的风速最大误差及最小误差均处于5种方法误差区间的偏低位置，有效降低了风速的最大及最小误差。

由7种方法在三类站点四个季节预报的风速整体平均误差可看出(表1)：对于不同季节、不同地形高度的站点均表现为集成方法1与反距离权重法的预报误差较小，集成方法2、3比另外3种降尺度方法的预报误差小，即集成方法在一定程度上降低了风速预报误差，其中滚动样本长度最短的集成方法预报效果相对较好。因此，对于精细化站点风速预报，宜采用反距离权重法或集成方法1。

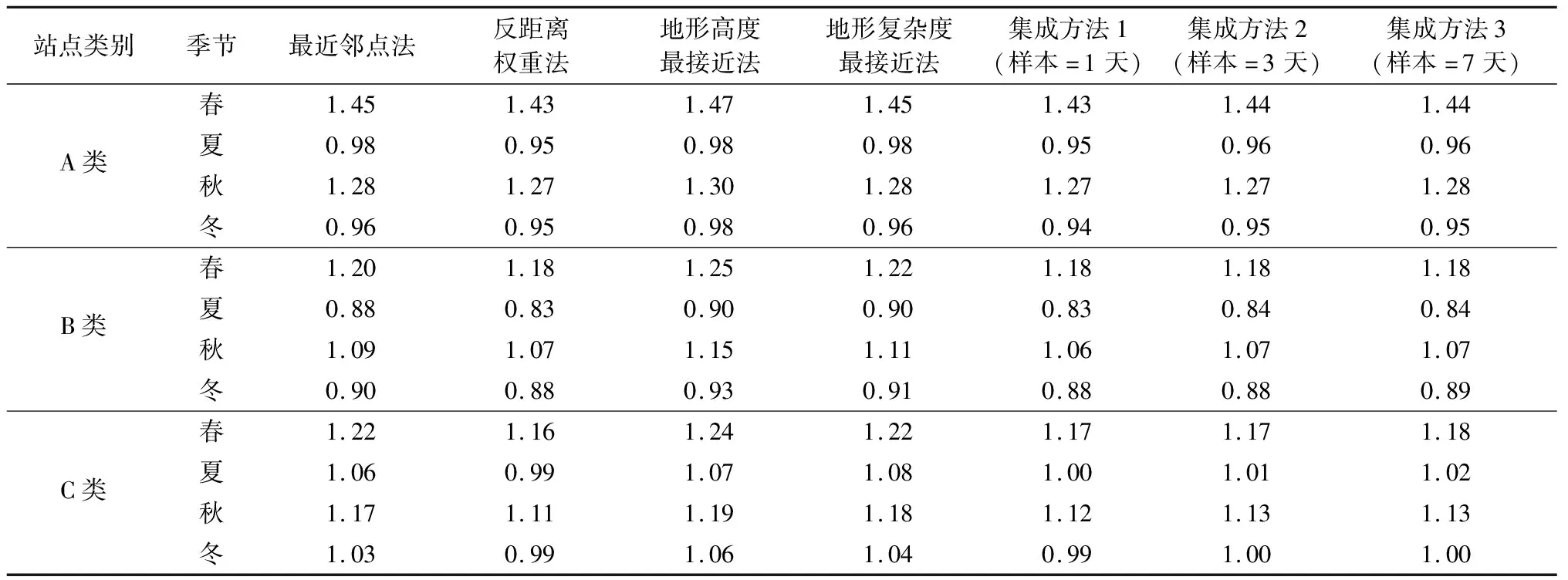
表1 7种方法在三类气象站的风速整体平均误差 m/s

对比不同季节的风速预报效果发现，夏季与冬季风速预报效果最好，其次为秋季的，春季的预报效果最差；不同季节的风速预报准确性与地形高度有一定相关，例如对于春季及秋季，A类站点预报误差明显高于B、C类站点的。

3.1.2 温度预报结果分析

分析7种方法在三类站点四个季节预报的温度日平均误差发现，四个季节的检验结论基本一致(以春季为例，其余季节图略)：对于地势平坦的A类站点(图2a)，7种方法的日平均误差差异较小，反距离权重法与集成方法预报效果相对较好，地形高度最接近法的次之；随着地形高度的增加，预报误差逐渐增加，对于地势较高的B、C类站点(图2b、2c)，4种降尺度方法的误差差异明显增大，反距离权重法、地形复杂度最接近法及最近邻点法的预报误差明显增加，此时地形高度最接近法与动态集成方法的预报效果较好。分析7种方法处理后的温度相同时刻平均误差的逐时演变发现(图略)，三类站点逐时平均误差的检验结果与日平均误差的检验结果大体一致。

图2 2018年4月7种方法在三类气象站的温度逐日平均误差

对比分析4种降尺度方法和第一种集成方法处理后的三类站点中相同时刻下温度最大及最小误差发现，经过集成方法处理后的温度最大误差及最小误差均处于5种方法误差区间的偏低位置(图略)，在一定程度上提高了温度预报的准确率及稳定性。

由7种方法在三类站点四个季节预报的温度整体平均误差可看出(表2)：对于不同季节的站点温度预报，地形高度较低时，集成方法与反距离权重法预报效果相对较好；随着地形高度的提升，集成方法与地形高度最接近法预报效果相对较好；3种集成方法中，样本长度最短的集成方法1预报效果相对较好。因此，对于精细化站点温度预报，地形高度较低时，宜采用集成方法1及反距离权重法；随着地形高度的提升，宜采用集成方法1及地形高度最接近法。

表2 7种方法在三类气象站的温度整体平均误差 ℃

对比不同地形高度的站点预报效果发现：对于A、B类站点，7种方法的预报误差差异较小，且均低于1.6 ℃；随着地形高度及复杂度的提升，7种方法的预报误差及差异性均明显增加。对比不同季节的温度预报效果可看出：秋季温度预报效果相对较好，夏季的次之，春季与冬季的预报效果最差。

3.1.3 湿度预报结果分析

分析7种方法在三类站点四个季节预报的湿度日平均误差发现，夏季与秋季的检验结论一致，春季与冬季的检验结论一致(以夏季、冬季为例，其余季节图略)：对于地势平坦的A类站点，动态集成方法与普通降尺度方法的预报效果基本一致(图3a、4a)；随着地形高度及复杂度的提升，误差和差异明显增大，3种集成方法的预报效果依旧较好，其中滚动样本最短的集成方法预报效果最好。夏季及秋季时(图3b、c)，4种普通降尺度方法中反距离权重法预报效果相对较好；春季及冬季时(图4b、c)，4种普通降尺度方法中地形高度最接近法预报效果相对较好。分析7种方法处理后的湿度相同时刻平均误差的逐时演变发现(图略)，三类站点逐时平均误差的检验结果与日平均误差的检验结果大体一致。

图3 2018年7月7种方法在三类气象站的湿度逐日平均误差

图4 2018年1月7种方法在三类气象站的湿度逐日平均误差

对比分析4种降尺度方法和第一种集成方法处理后的三类站点中相同时刻下湿度最大及最小误差发现，集成方法与4种方法的湿度预报最小误差差异较小，但集成方法的湿度预报最大误差稳定处于5种方法误差区间的偏低位置，有效降低了湿度预报误差。

对比7种方法在三类站点四个季节预报的湿度整体平均误差发现(表3)，不同季节、不同地形高度的站点最佳预报方法不一：春季和冬季时，宜采用集成方法与地形高度最接近法；夏季和秋季时，宜采用集成方法与反距离权重法。整体来看，4种普通降尺度中，反距离权重法与地形高度最接近法预报效果相对较好；3种集成方法中，样本长度最短的集成方法1预报效果相对较好。

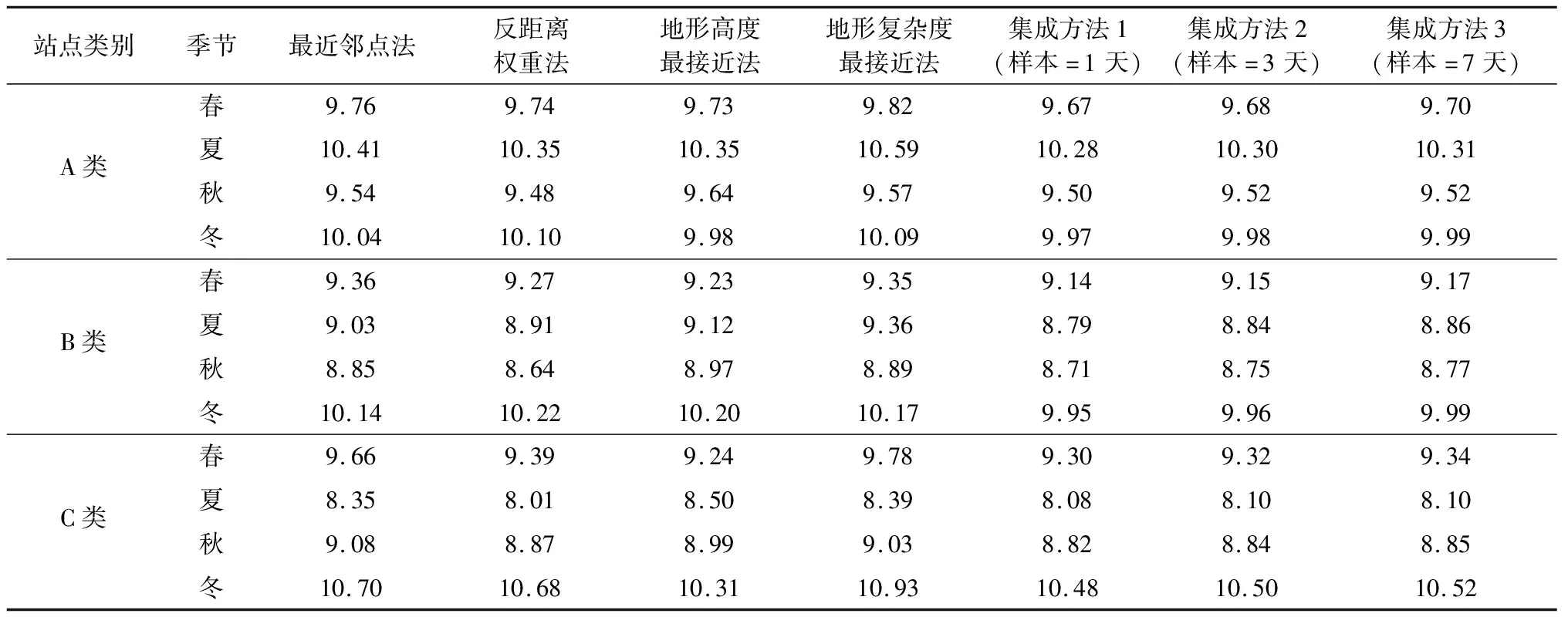
表3 7种方法在三类气象站的湿度整体平均误差 %

对比不同季节的湿度预报效果看出，不同季节的湿度预报效果在一定程度上受地形的影响：夏季时误差随地形高度的提升而降低；与夏季相反，冬季时误差随地形高度的提升而增加；春季与秋季时误差随地形高度的提升呈先降低后增加的变化趋势。此外，随着地形高度的增加，预报的湿度误差季节差异逐渐变大。

3.2 大风天气过程预报性能评估

基于2018年1月、4月、7月、10月的气象站风速观测数据，判定大部分站点10 min平均风速为4级风以上的日期为一个大风天。按此标准，共筛选了6个大风天。分析7种方法处理后的大风天风速平均误差发现：对于地势平坦的A类站点，7种方法的平均误差差异较小，除了第4个大风天反距离权重法预报效果相对较好外，其余5个大风天地形复杂度最接近法预报效果较好，样本长度最短的集成方法的次之。随着地形高度的提升，地形高度最接近法预报效果显著提升，地形复杂度最接近法预报效果相对变差。其中，对于B类站点，前3个大风天及第6个大风天，地形高度最接近法预报效果较好，第4、5个大风天，反距离权重法效果较好；对于C类站点，7种方法的平均风速误差差异明显增大，地形高度最接近法预报效果依旧较好，其次为反距离权重法的预报效果。

对比大风过程中7种方法在三类站点预报的风速整体平均误差发现(表4)：对于A类站点，宜采用地形复杂度最接近法或集成方法1；对于B类站点，宜采用地形高度最接近法或反距离权重法；对于地形高度较高的C类站点，宜采用地形高度最接近法，其次为反距离权重法。因此，在无天气过程下风速预报宜采用的反距离权重法不再普遍适用于大风过程，且集成方法的优越性很难在大风过程中体现，尤其是对于地形高度偏高的B、C类站点。

表4 大风过程下7种方法在三类气象站的风速平均误差 m/s

4 结 论

本文基于最近邻点法、反距离权重法、地形高度最接近法、地形复杂度最接近法，以及基于4种降尺度方法的动态集成方法(滚动样本=1天、3天、7天)共7种方法，利用GDFS逐小时预报数据及气象站观测数据，探讨了7种方法对河南省2018年四个季节、不同地形高度气象站的风速、温度及湿度的预报效果，主要结论如下：

(1)多方案动态集成方法，避免了单一预报方法造成的不稳定性和不确定性，整体上有效提高了风速、温度、湿度的预报准确率及稳定性，适用于不同季节及不同地形条件，尤其是滚动样本长度最短的动态集成方法，预报提升效果最为显著。

(2)从整体预报性能评估来看，对于精细化站点风速预报，宜采用反距离权重法或样本长度最短的动态集成方法。对于大风过程下的精细化站点风速预报，地形高度较低时，宜采用地形复杂度最接近法或集成方法1；地形高度偏高时，宜采用地形高度最接近法或反距离权重法。

(3)对于精细化站点温度预报，地形高度较低时，宜采用样本长度最短的集成方法及反距离权重法；随着地形高度的提升，7种方法的预报误差差异明显增大，宜采用样本长度最短的集成方法及地形高度最接近法。不同季节中，秋季的预报误差相对较小。

(4)对于精细化站点湿度预报，夏季及秋季时，宜采用样本长度最短的集成方法及反距离权重法，春季及冬季时，宜采用样本长度最短的集成方法及地形高度最接近法。

(5)对于风速、温度、湿度要素，不同季节的预报准确率在一定程度上均受地形高度影响。