2018年10月-2019年9月太原大气能见度与相对湿度及PM2.5浓度的关系研究
卢盛栋,赵桂香,金 磊,李 强
(1.山西省气象灾害防御技术中心,太原 030012;2.山西省气象台,太原 030006)
大气能见度与人们生活密切相关,低能见度往往诱发交通事故,造成飞机延误等。近年来,大气能见度的变化已引起各界重视。相关研究表明[1-10],大气能见度不仅与当地污染物有关,还与相对湿度及颗粒物浓度密切相关。吕建华等[10]研究表明,济南市大气能见度与相对湿度、细颗粒物浓度有明显的月变化和日变化规律。济南市大气能见度与相对湿度的相关系数为0.6501,与PM2.5浓度的相关系数为0.7422。吴雁等[11]对河北中南部城市大气能见度与细颗粒物浓度进行了分析,发现PM10和PM2.5浓度与能见度呈显著的负相关关系,且与PM2.5浓度相关性更加显著。此外,当大气中污染物浓度较高时,较小风速不能促使污染物扩散,也会出现低能见度现象[12-15]。
关于大气能见度与颗粒物浓度及相对湿度的关系模型研究,广大学者也进行了探讨[16-20]。胡海川等[17]研究了神经网络在环渤海地区能见度预报中的应用,发现该方法对低能见度天气过程的能见度预报效果良好,能见度低于10 km的预报误差为4~6 km。白永清等[18]揭示了武汉大气能见度与PM2.5浓度存在的非线性相关关系,用神经网络方法得到了武汉地区大气能见度预报模型。宋明等[19]利用相对湿度、PM2.5及PM10浓度数据,用指数函数拟合了能见度与PM2.5及PM10浓度的关系,用非线性拟合的方法得到了天津地区大气能见度预报公式。王晓敏等[20]利用指数函数拟合了能见度与相对湿度的关系,并用非线性拟合方法得到了石家庄地区能见度预报公式。这些模型对本地区能见度预报都有一定的适用性。
太原作为山西省省会,重工业比较集中,三面环山,大气常处于一种静稳状态,不利于颗粒物的扩散,常造成低能见度天气[21]。相比于长江三角洲、京津冀等发达地区,关于太原地区大气能见度的研究较少。卢盛栋等[21]分析了太原大气能见度月平均最大值出现在5月,月平均最小值出现在1月。管琴等[22]利用2009年太原地区日平均能见度、相对湿度、空气污染指数进行拟合,建立了太原地区雾天能见度预报模型,该模型有一定适用性。由于近几年太原城市扩容加速,与南边的晋中市榆次区、太谷区同城化发展,都市圈中心逐渐南移,特别是近几年山西转型发展步伐加快,污染物传输也发生了改变,相对湿度、颗粒物浓度对能见度的影响发生了变化,因此本文利用2018年10月-2019年9月太原地区能见度、相对湿度及PM2.5质量浓度逐小时观测数据,研究分析了大气能见度与相对湿度及PM2.5浓度的关系,采用多元非线性拟合[23-24]及神经网络[25-29]方法构建了能见度预报模型,并利用太原地区近期气象数据对两种预报模型进行了检验及对比分析,以期为太原地区能见度预报提供参考。
1 资料与方法
利用2018年10月-2019年9月太原小店区气象观测站(112.55°E、37.75°N,海拔776.2 m)大气能见度(传感器型号:HY-V35)、相对湿度(传感器型号:HMP155)、PM2.5浓度(传感器型号:TEOM-1405D)逐小时观测数据,经质量控制去掉奇异值,分析能见度与相对湿度及PM2.5浓度的定量关系,并利用非线性拟合及神经网络方法构建了能见度预报模型。
非线性拟合是采用迭代法对模型进行拟合,应用非线性最小二乘法确定参数取值范围,根据可决系数比较拟合效果,选取误差最小的模型,确定自变量与因变量之间的非线性关系。本文非线性拟合借助SPSS软件完成。
神经网络具有良好的处理非线性问题的能力,有信号前向传递、误差反向传播的特点[30]。采用输入层、隐含层、输出层三层结构,在前向传递中,输入信号从输入层、隐含层逐层处理至输出层,如果输出层得不到期望值,则转入反向传播,根据误差不断调整权值和阈值,使输出不断逼近期望值[21]。本文隐含层节点数设定为10,一般情况下提高隐含层节点数可以提高神经网络收敛精度,但隐含层过多,会出现过拟合现象,对样本识别能力下降。本文神经网络模型是通过MATLAB软件编程实现的。
在对预报模型进行检验时,用到均方根误差(ERMS)、平均绝对百分误差(EMAP)。计算方法如下:
(1)
(2)
式(1)—(2)中,P代表预报值,O代表观测值,N代表检验样本个数。
2 结果与分析
2.1 太原大气能见度与相对湿度的关系
利用太原地区2018年10月-2019年9月相对湿度及能见度逐小时数据(除去降水及奇异值,样本量为6153),统计分析不同相对湿度对应的平均能见度及平均PM2.5浓度数据,散点图见图1。由图1可知,当相对湿度RH<40%时,随着RH升高能见度下降相对较快,对应PM2.5浓度也上升较快;当相对湿度40%≤RH<90%时,随着RH升高,PM2.5浓度基本不变(图1b),能见度下降缓慢(图1a),出现图1(a)第一个拐点(横坐标40%对应的点,属于两种拟合曲线交叉点);高湿条件下,即RH≥90%时,随着RH升高,能见度急剧下降,出现图1(a)第二个拐点(横坐标90%对应的点,属于两种拟合曲线交叉点)。这也与曹军骥等[31]的研究比较一致,即随着相对湿度的升高,可溶性气溶胶吸湿潮解造成散射效率显著增强,能见度恶化,当相对湿度RH≥90%时,这种现象更为显著。
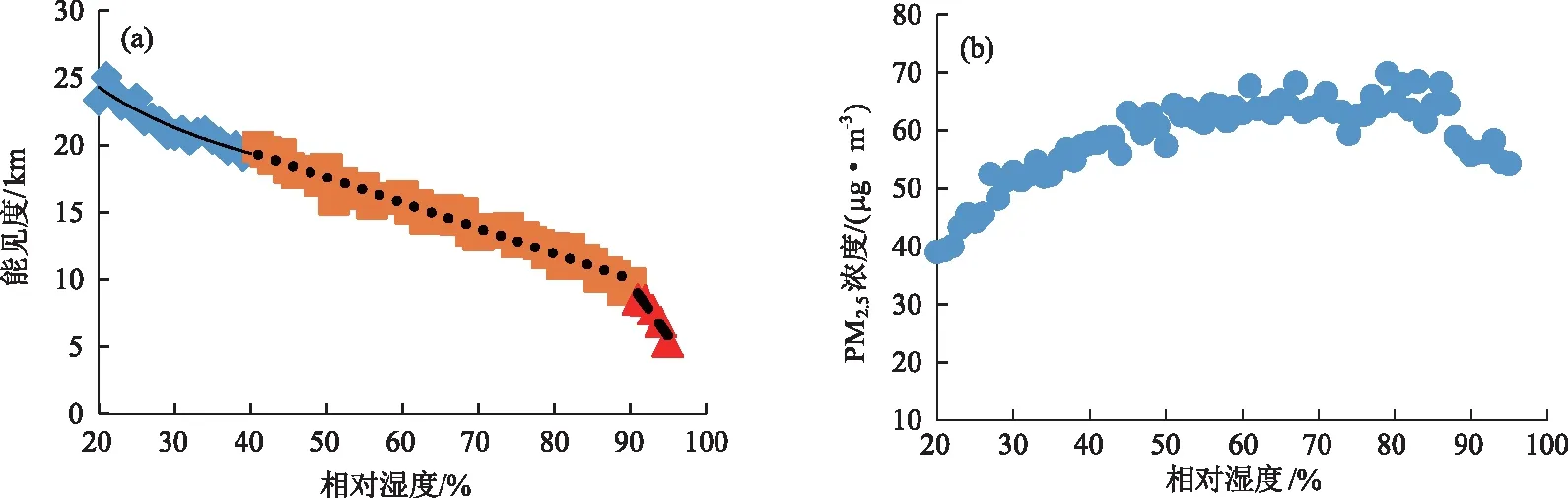
图1 太原大气平均能见度、PM2.5浓度与相对湿度的关系
由图1(a)的散点图,得出太原地区大气能见度(V)与相对湿度(RH)的定量关系式如下:
(3)
当RH<40%时,太原大气能见度与相对湿度成幂函数关系,如式(3)所示,二者相关系数达到0.93;当40%≤RH<90%时,太原大气能见度与相对湿度呈线性关系,相关系数达到0.96,且在此条件下,相对湿度每增加1%,太原平均能见度降低0.188 km;当RH≥90%时,太原大气能见度与相对湿度呈二次多项式关系,相关系数为0.97,且在此高湿条件下,随着相对湿度增加,能见度急剧下降。
2.2 太原大气能见度与PM2.5浓度的关系
依据2018年10月-2019年9月太原小店区逐时气象数据及颗粒物浓度数据,分析PM2.5浓度对能见度的影响。为尽可能消除相对湿度对能见度的影响,本文将相对湿度分成五个区段进行分析[18],并采用幂函数拟合PM2.5浓度与能见度的散点关系,如图2所示。
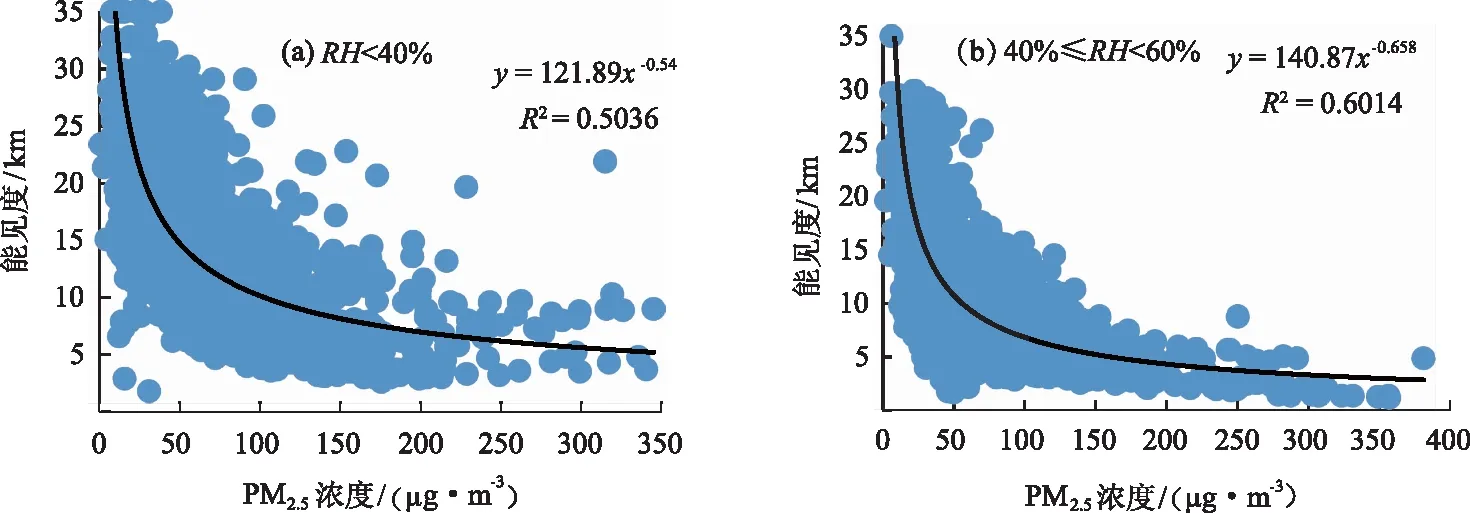
图2 不同湿度区段下太原地区大气能见度与PM2.5浓度的拟合关系
白永清等[18]得出PM2.5浓度与武汉地区大气能见度的相关系数为0.73~0.84,而太原地区各湿度段二者相关系数指标为0.32~0.67(见表1),特别当RH≥90%时,二者相关系数仅为0.32,模型拟合较差,但都通过了0.01的显著性水平检验。此外,相对湿度在80%≤RH<90%区段下,武汉能见度与颗粒物相关性最强[18],广州在40%≤RH<60%区段下的相关性最强[32],而太原在40%≤RH<60%区段下,决定系数为0.60,相关系数为0.67,该时段相关性最强,表现出的地域性差异,可能与太原三面环山北高南低特有的地形有关。
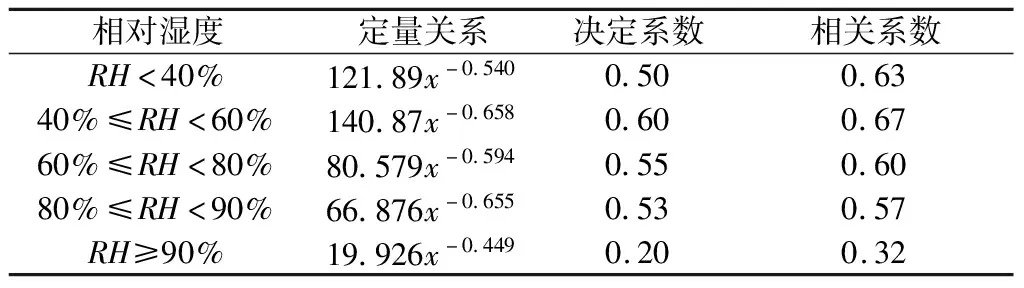
表1 不同湿度区段下太原地区大气能见度与PM2.5浓度的拟合方程
2.3 能见度预报模型
2.3.1 非线性拟合构建预报模型
由以上分析可知,相对湿度与PM2.5浓度对大气能见度影响显著,现以其为因变量,将相对湿度分成五个区段,利用SPSS软件对大气能见度进行多元非线性拟合,结果如下:
V=a×RHb+c×ρ(PM2.5)d+e
(4)
式(4)中,V代表大气能见度,RH代表相对湿度,ρ(PM2.5)代表PM2.5浓度,a-e为系数。从拟合结果看(见表2),均方根误差、平均绝对百分误差分别在4.59~6.71 km、25.99%~63.56%。当RH<90%时,相关系数在0.70左右,当RH≥90%时,模型较差些,相关系数仅为0.40,但都通过了0.01的显著性检验,说明该模型对大气能见度具有一定的预报能力。

表2 不同湿度区段下大气能见度与相对湿度及PM2.5浓度的非线性拟合系数
2.3.2 神经网络构建能见度预报模型
将相对湿度和PM2.5浓度预报因子作为输入端,能见度预报值作为输出端,采用太原地区2018年10月-2019年9月逐时数据,分为两段,前3/4长度为训练期,后1/4作为预报期,构建神经网络大气能见度预报模型。
神经网络模型在预报期内模拟与实况值的变化趋势基本一致,特别是对低能见度样本,模拟效果更佳(见图3)。对神经网络构建的大气能见度预报模型进行检验,相关系数为0.82,均方根误差为3.42 km,平均绝对百分误差为26.15%。对比非线性拟合结果,相关系数为0.40~0.76,均方根误差为4.59~6.71 km,平均绝对百分误差为25.99%~63.56%,神经网络预报模型更具有较高准确性。

图3 神经网络模型预报期内能见度预报与实况对比
2.4 预报模型验证
2020年1月,太原地区低能见度现象频发,全月低能见度天气现象占全月总比达70%,特别是在1月8-12日,太原地区出现连续5 d的低能见度,城区实行了交通管制。为此,利用太原市小店区2020年1月1-31日气象小时数据对模型进行验证。
图4为两种模型的预报效果。由图4可以看出,两种预报模型对能见度都有一定的预报能力。非线性模型的预报值偏高且较为分散,神经网络预报值更向对角线集中。由两个模型的预报结果(表3)可知,神经网络预报模型预报值与实况值的相关系数提高到了0.91,均方根误差仅为2.77 km,平均绝对百分误差降到了24.88%。
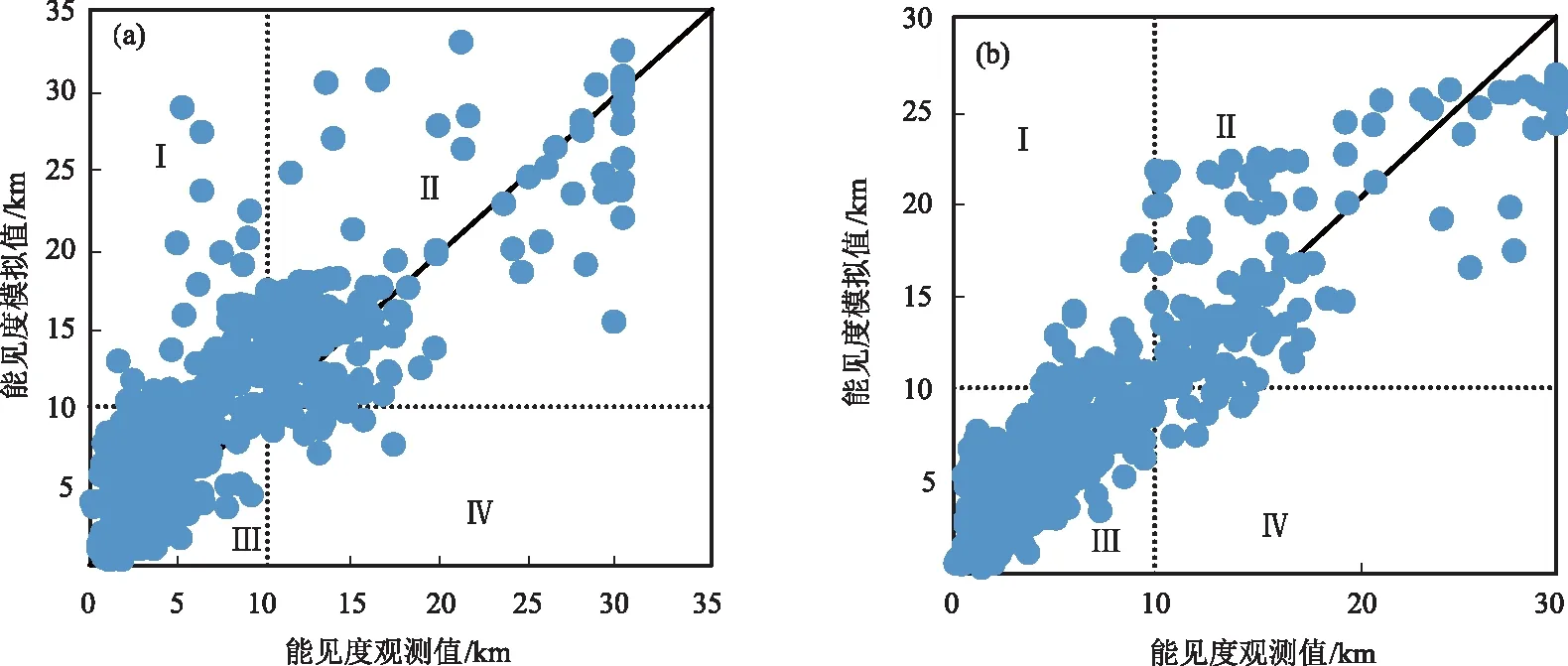
图4 非线性预报模型(a)和预报模型(b)的预报效果

表3 两种不同预报模型的检验参数
以低能见度阈值10 km为分界线[33]进行分级检验,将图4中分成四个区域(图中虚线部分)Ⅰ、Ⅱ、Ⅲ、Ⅳ,落在各自区域的点数分别为a、b、c、d,根据散落在各自区间的点数代入对应公式分别计算预报准确率、漏报率、空报率[28,34],以此来评价其预报能力,统计结果见表4。由表4可知,两种预报模型对大气能见度都有一定的预报能力。非线性拟合的预报准确率高达84.53%,神经网络的准确率提高到了93.78%;非线性拟合模型的漏报率较高,神经网络模型的漏报率降至6.34%;两种预报模型的空报率都较低,神经网络模型的降至1.85%。两种预报模型的误差频率分布都较好地服从正态分布(见图5),但神经网络模型的误差集中在2 km以内,落在该区域的频率达74.72%,非线性拟合的误差较为分散,主要集中在4 km以内,落在该区域的频率为90.74%,在2 km以内的频率仅为63.26%。

表4 两种不同预报模型的分级检验
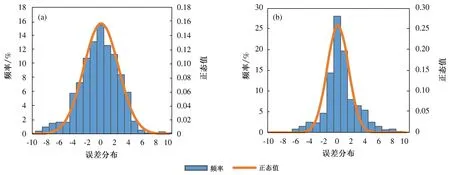
图5 非线性预报模型(a)和神经网络预报模型(b)误差的频率分布
综上分析,两种模型对大气能见度都有一定的预报能力,但神经网络模型预报能力更强。由于神经网络模型比较抽象,非线性拟合模型参数比较固定,在实际应用中可以将两者结合起来使用。
3 结论与讨论
利用2018年10月-2019年9月太原小店区相对湿度、PM2.5浓度、能见度逐小时观测数据,分析了能见度与相对湿度、PM2.5浓度的关系,利用非线性拟合及神经网络方法,构建了关系模型,并进行了检验,得到以下结论:
(1)细颗粒物浓度与相对湿度对太原大气能见度有明显影响。当RH<40%时,能见度降低主要是由PM2.5浓度逐渐升高影响,能见度与相对湿度呈非线性关系;当40%≤RH<90%时,能见度与湿度呈线性关系,湿度每增加1%,太原大气能见度平均降低0.188 km;当RH≥90%时,随着相对湿度增加,能见度急剧下降。不同湿度条件下,太原大气能见度与PM2.5浓度呈幂函数关系,相对湿度在40%≤RH<60%区段下相关性最强。
(2)不同相对湿度条件下非线性拟合的大气能见度预报模型的相关系数为0.40~0.76,均通过了0.01的显著性水平检验,均方根误差为4.59~6.71 km,平均绝对百分误差为25.99%~63.56%,拟合模型在RH<90%时,拟合效果最佳。神经网络构建的大气能见度预报模型预报性能良好,相关系数为0.82,均方根为3.42 km,平均绝对百分误差为26.15%。
(3)利用太原小店区2020年1月小时数据对非线性拟合模型和神经网络模型进行了验证,结果表明,两种模型对太原地区大气能见度都有一定的预报能力,但神经网络模型预报准确率达93.78%,漏报率和空报率都比非线性拟合模型的低,且误差分布比较集中,集中在2 km以内的达74.72%,非线性拟合模型的误差分布较分散,多集中在4 km以内,在2 km以内的误差达63.26%。神经网络模型较非线性模型预报结果更准确,但非线性模型更形象,实际业务中可以将两者结合使用。
影响能见度的气象因子较多,如风速、风向及高空气象要素等对能见度也有影响,且文中资料数据仅为2018年10月-2019年9月的,观测站点为小店观测站,在后期研究中将进一步增加能见度气象影响因子,延长时间序列及站点序列,以得到更准确的能见度模型。

