超弹性N 形杆纯弯曲力矩理论建模和试验验证
杨 慧,王金瑞,冯 健,刘荣强
(1.安徽大学电气工程与自动化学院,合肥 230601;2.哈尔滨工业大学机电学院机器人技术与系统国家实验室,哈尔滨 150080)
由于航天器的运载存储能有限,对大型空间可 展开结构的使用越来越多[1],如太阳帆[2]、反射器天线等。超弹性杆因其性能优异而成为可展结构的重要组成部分,它能通过释放在弯曲缠绕过程中储存的应变能实现自展开[3⁃4]。在宇航空间中,超弹性杆能否顺利展开关乎空间任务的成败。目前在研究中的超弹性杆有带簧、豆荚杆、人形杆等,为了研究超弹性杆的力学性能,国内外学者已经通过解析法、试验验证和仿真法等对其进行了多方面研究。Kwok 等[5]在考虑黏弹性的基础上推导了带簧弯曲后力矩松弛的解析表达式。Pellegrino 等[6]研究了螺旋缠绕的带簧的稳定性;Footdale 等[7]以带簧为臂架设计了一种自展开薄膜机构;Yasuyuki等[8]推导了带簧绕轮毂时的缠绕力矩和应变能的理论模型,并用实验验证了理论的准确性;Leclerc等[9]提出了一种人形杆的制备方法,并对人形杆在卷曲和展开时的应力集中和失效行为进行了研究;Stabile 等[10]采用仿真法对C 形杆的压扁缠绕进行分析,通过参数分析得到了强度较好的C 形杆参数;叶红玲等[11]对折叠缠绕时的带簧进行了几何参数优化。
白江波等[12⁃13]采用真空袋成形和复合工艺制备了豆荚杆,并采用有限元分析方法和真空试验探究了豆荚杆在空间环境中的热行为;Chu 等[14]提出一种豆荚杆为骨架的可展开机构,并对其动力学行为和尺寸参数的鲁棒自适应性进行了研究;Chen等[15]对豆荚杆的拉扁、压扁过程进行了实验和仿真分析比较;Li 等[16]基于试验和仿真分析,对豆荚杆复合材料的缠绕过程进行分析;中国科学院的范文杰等[17]提出了一种新型X 形截面弹性杆,在同样的收拢高度下,它具有更高的截面惯性矩。Yang等[18]以展开状态的弯曲刚度和扭转刚度对N 形杆的几何参数进行了优化,但对其缠绕过程中的力矩还未从理论上进行分析。本文对其缠绕过程进行理论分析和试验验证。N 形杆如图1 所示,N 形杆是由3 个横截面具有一定曲率的薄壁壳体粘贴在一起组成的。基于协变量向量法建立了单片带簧的应变能和弯矩的理论模型,然后建立了扁平段和偏离对称轴一定距离的带簧的弯矩模型,最后通过拟合曲率的方法建立了N 形杆弯矩的理论模型。研制了4 根相同的N 形杆样件,搭建了试验平台,分别测试了4 根N 形杆在缠绕时的拉力,求出力矩,通过试验来验证N 形杆理论模型的准确性。

图1 N 形杆截面Fig.1 Cross section of N⁃shaped boom
1 单片带簧力矩建模
1.1 几何关系
带簧如图2(a)所示,曲率半径为R,厚度为t,圆心角为θ。建立惯性笛卡尔坐标(i1,i2,i3),正交坐标系(x,y,z)和对应的标准正交基向量(Hx,Hy,Hz)。x沿 平 行 于i1的 纵 向,y轴 沿 弧 线 方 向,z轴 沿 厚 度方向指向圆心。(Hx,Hy,Hz)与(i1,i2,i3)的关系如下
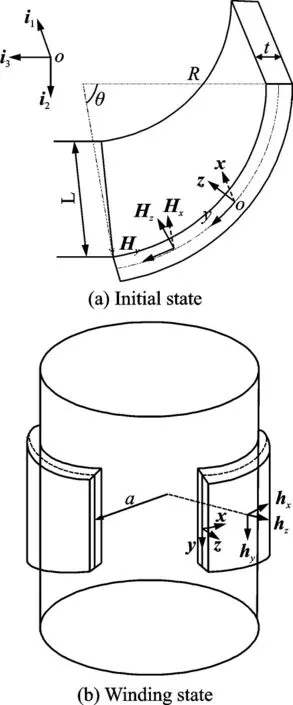
图2 初始和缠绕状态Fig.2 Initial and winding states
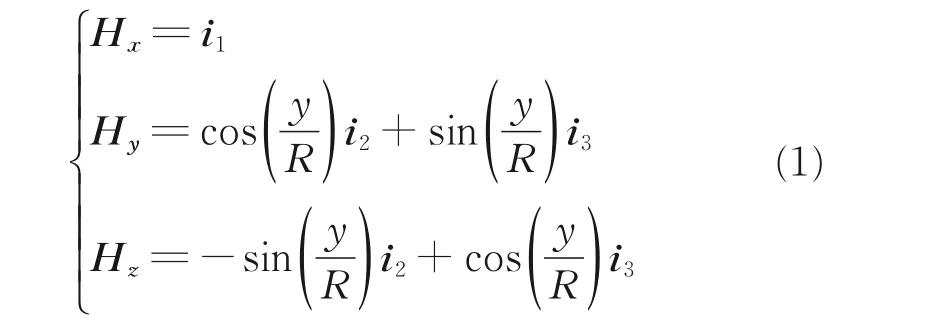
壳层中任意一点在初始状态下的位置向量X表示为

对其x、y、z方向求导,可得协变基向量Gx、Gy、Gz为

带簧在纯弯曲缠绕状态下的小位移为(u,v,w),在Kirchhoff⁃Love 假设下,变形状态下的位置向量x可表示为

式中x0为带簧中面的位置向量,即

假设u是关于x的函数;v、w是关于y的函数;带簧的厚度t远远小于半径R和长度L,且壳体表面上的应力是均匀分布的。
对x求导,对应的协变基矢量gx、gy、gz为

式中k=1/a。
对称弯曲变形时只有x、y、z方向的轴向应变,由前面的假设可以知道应变项中的t/R的二阶或者更高阶可以忽略不计,则x、y轴的应变εxx和εyy可表示为

1.2 平衡方程

式中:b1=1/2Rθ1;sxx、syy分别表示x、y方向应力;δexx、δeyy、δw、δv、δu为虚应变;Tedge、Nedge、Medge分别表示在y=b时,y方向,z方向每单位长度的外力和x方 向 每 单 位 长 度 的 外 力 矩;Tend、Mend分 别 为x方向外力和y方向外力矩。

图3 壳体单位受力图Fig.3 Diagram of shell unit force

纯弯曲条件下力和力矩的定义如下

将式(11)和式(12)代入壳体平衡方程式(10),可得



1.3 应变能和力矩

1.4 扁平段弯矩模型
扁平段如图4 所示,由前述分析可知,扁平段的应变能可表示为
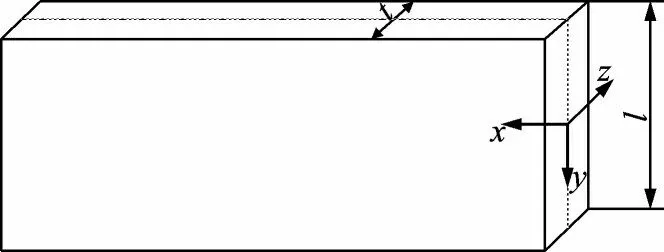
图4 扁平段Fig.4 Flat segment

式中:πxl为扁平段由凸变平的应变能,πyl为缠绕产生的应变能。
扁平段的初始曲率为0,在缠绕时它只经历了曲率为k的缠绕过程,即

2 离对称轴距离为S 的带簧弯矩建模
2.1 几何关系和挠度
带簧如图5(a)所示,与第1.1 节图2(a)相同,建立相同的惯性笛卡尔坐标(i1,i2,i3)、正交坐标系(x,y,z)和对应的标准正交基向量(Hx,Hy,Hz)。N形杆横截面如图5(b)所示,其外侧带簧离对称轴的距离为s,在缠绕后其中面的位置向量x表示为

图5 N 形杆截面和带簧初始状态Fig.5 Initial state of tape spring and cross section of N⁃shaped boom

由于边界条件相同,建立的平衡方程与式(11)相同,经计算可得挠度w为

2.2 应变能和力矩
由1.3 节分析可知,带簧的应变能可表示为

经计算,可得应变能和弯矩为
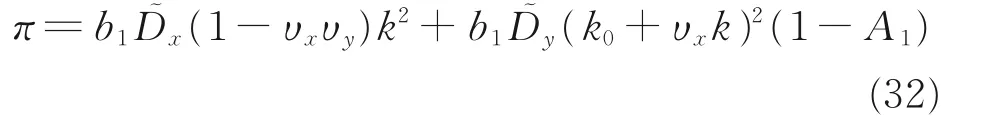
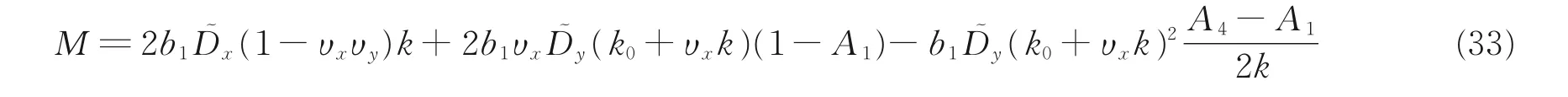

采用协变基向量法对偏离对称轴距离为0 和S的带簧的理论推导中,发现两者的弯矩和应变能的理论模型相同,但在挠度上有差别,相差的大小为S。下面将推导N 形杆的弯矩解析解。
3 N 形杆理论建模
3.1 几何分析转化
N 形杆初始状态如图6(a)所示。在初始状态下,左右反对称分布,对称中心左右两部分都是由一端圆心角为θ1、半径为R的带簧,一段粘合的线段l,以及一段圆心角为θ2、半径为R的带簧组成,每一片的厚度均为t。
N 形杆缠绕后的曲率如图6(b)所示,中心曲率为k=1/a0,内 边 曲 率kin=1/(a-3t/2),外 边 曲率为kout=1/(a+3t/2)。以N 形杆曲率半径a0处为分界线,将其分为内外两组。

图6 N 形杆缠绕过程和完全缠绕的状态Fig.6 Winding process and state of complete winding of N⁃shaped boom
内组为杆1 和杆2 对称分布,其中心曲率为kA=1/(a0-t/2),内边曲率为k1=1/(a0-3t/2),外边曲率为k2=1/a0。外组中杆3 和杆4 对称分布,其中心曲率为kB=1/(a0+t/2),内边曲率为k3=1/a0,外边曲率为k4=1/(a0+3t/2)。
3.2 应变能的计算

式中,πin1和πout2是由一段圆心角为θ1、半径为R的带簧(b2=1/2Rθ2,b1=1/2Rθ1)加一段长为l的扁平段的应变能组成,但它俩初始曲率方向不同,即
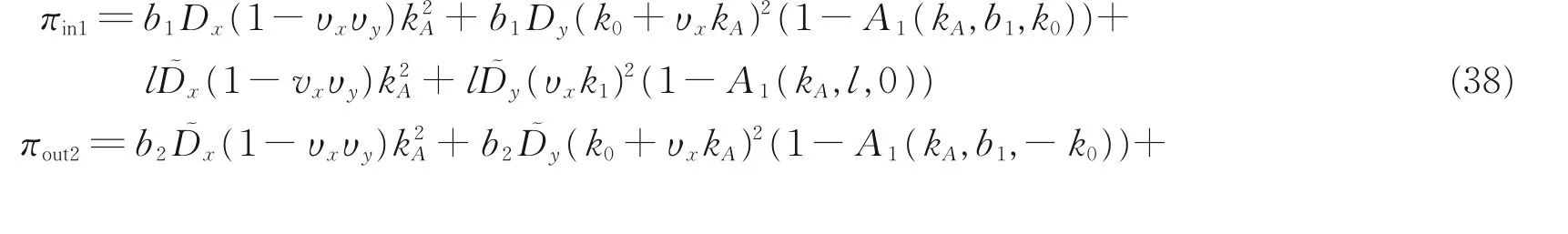

3.3 弯矩的求解
基于最小势能原理,可以推导出弯矩为

将式(42)代入式(43),得


3.4 理论曲线
N 形杆材料参数如表1 所示,其外侧圆弧角θ1=1.45 rad,内侧圆弧角θ2=0.45 rad,直线段长度l=11 mm,厚度t=0.14 mm,初始曲率半径为R=20 mm。将参数代入式(33),得到力矩⁃曲率曲线如图7 所示。在开始时,力矩随曲率迅速上升到峰值0.242 5 N·m,之后又迅速下降,趋于稳定。

表1 N 形杆材料参数Table 1 Material parameters of N‑shaped boom

图7 N 形杆理论曲线Fig.7 Theoretical curve of N⁃shaped boom
峰值力矩能够表征N 形杆在展开状态下抵抗外力的能力,代表着整个机构的刚度大小,为此,搭建试验平台对其进行测量。
4 N 形杆缠绕试验
为了进行N 形杆缠绕试验,研制了4 根相同的N 形杆样件如图8(a)所示,搭建试验平台对缠绕过程中的力矩进行测试,试验平台如图8(b)所示。将N 形杆一端固定于轮毂,利用推拉力计带动连接在轮毂上的臂杆旋转,进而带动N 形杆实现缠绕。推拉力计的型号为(HP⁃10),量程为10 N,灵敏度为0.001 N,其另一端连接数据采集系统,可输出测试过程中的拉力。

图8 N 形杆和弯曲试验装置Fig.8 N⁃shaped booms and experimental device
推拉力计测量的拉力乘以力臂长度,可以得到N 形杆缠绕时的力矩M,即

式中:M和F分别为力矩和拉力,L为力臂长度。
四根N 形杆样件分别用N1、N2、N3 和N4 表示,对每根N 形杆分别进行了5 次测试,得到试验的峰值力矩、峰值力如表2 所示。
为了验证理论模型的准确性,用偏差和偏差标准差来表示理论值和试验值误差的大小,即
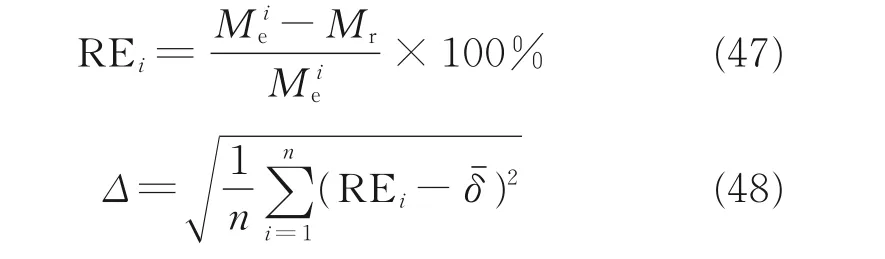
式中:Mie、Mr分别为试验值、理论值,i为第i个测试数据,n为测试总数,δˉ为偏差均值。
将表2 中测得的峰值力矩代入式(47)中对应的试验值Mie,得到N 形杆缠绕过程中,试验值与理论值的偏差值不大于8.83%,偏差平均值为2.813%,偏差标准差为4.97%,验证了理论模型的准确性。但其中仍存在误差,误差来源主要有以下几方面:N 形杆与轮毂之间、N 形杆与导向杆之间存在摩擦;推拉力计与力臂之间存在小幅度滑动;在缠绕过程中,推拉力计的方向与力臂的方向不是完全垂直的;试验件N 形杆的尺寸存在偏差。

表2 4 根N 形杆的峰值力和峰值力矩Table 2 Peak forces and peak torques of four N‑shaped booms
5 结 论
为防止N 形杆在缠绕时的失稳,通过理论建模得到了N 形杆在缠绕时的峰值力矩。通过试验验证并分析参数,得到了以下结论:
(1)基于协变量向量法建立了单带簧的应变能理论模型,采用最小势能原理推导了弯矩的表达式,然后采用相同方法对扁平段和偏离对称轴一定距离的带簧建立弯矩模型,最后拟合曲率建立了N形杆弯矩的理论模型。
(2)搭建试验平台,研制了4 根N 形杆样件,分别对每个N 形杆弯曲时的缠绕力矩进行5 次测量,并将其与理论值对比,得到偏差值不大于8.83%、偏差平均值为2.813%、偏差标准差为4.97%。

