冲压空气涡轮系统结构协同优化

夏天翔，卢岳良，柯 兵

（1.航空工业南京机电液压工程研究中心能源传动部，南京 211106；2.航空机电系统综合航空科技重点实验室，南京 211106）

随着飞机“多电技术”的发展，机上越来越多地使用电能作为主要能源系统[1⁃4]。冲压空气涡轮（Ram air turbine，RAT）系统作为一种机载应急能源系统，在飞机失去主、辅动力的紧急情况下，能将气流的冲压能转变为电能和液压能，维持飞机的可操控性。从用户角度出发，RAT 作为飞机必须背负的冗余设备应该在具备所需安全性、耐久性的同时具备最低的重量。因此，针对RAT 开展结构优化设计技术研究具有重要的工程应用价值。

RAT 平时贮存于RAT 舱内并由舱门保护。当飞机在空中失去主、辅动力后，RAT 由机体内释放以将冲压空气能转换为飞机能源。RAT 在全生命周期内可以分为两类运行场景——贮存场景（RAT 主要承受振动、过载、舱门气动力等载荷）和工作场景（RAT 主要承受运动冲击、气动力、气弹振动、过载等载荷）。RAT 在这两种运行场景下承受着不同的载荷工况。

目前，国内外学者已将结构优化设计广泛应用于工业制造领域[5⁃12]。这些结构优化设计方法中，适用于多工况约束的协同优化设计方法也有一些学者进行了工程应用：付雅婷等开展了多工况下的高速动车组运行速度控制优化[13]；陈宝等开展了面向多工况性能匹配的汽车悬架衬套多因素联合优化[14]；余知朴等研究了多工况下飞机货舱门开启功能的可靠性优化设计方法[15]；苏绍娟等开展了多工况应力约束下的船舶结构优化[16]；邹坤等开展了基于工况风险评估的叉车门架多工况拓扑优化[17]；钱杨等进行了基于分段动态松弛协同优化算法的船舶机舱结构优化设计[18]；高德峰等进行了基于协同优化自卸车卸料装置有限元优化分析[19]。

鉴于有关RAT 的研究主要集中于性能分析领域[20⁃23]，尚未涉及结构优化，本文以RAT 系统结构减重为研究目标，首先进行了RAT 运行场景和典型载荷工况分析，然后基于刚体动力学、结构力学、仿真等方法建立各工况下设计变量和约束的数学模型并基于敏感度分析确定了关键设计变量。最终，本文建立了RAT 结构的协同优化模型，并在此基础上基于Isight 多学科设计优化软件对某型RAT 系统进行了结构优化设计。

1 载荷工况与边界约束

1.1 系统组成

1.2 工况和约束分析

1.2.1 贮存场景

贮存场景下，RAT 不工作，随飞机日常飞行。此时，RAT 的载荷工况主要为基础振动和静力：

(1) 基础振动工况。指机体传递给RAT 的基础振动激励。为防涡轮振动过大导致叶片与舱门发生碰擦，在设计时通常会给出涡轮处的位移响应上限作为设计约束。

(2) 静力工况。包含由舱门连杆传递给RAT的舱门气动吸力和舱门过载力。由于相比于舱门，RAT 自身的过载力分布不均且较小，因此本文忽略RAT 自身的过载力。此工况下RAT 结构需满足强度约束。

1.2.2 工作场景

工作场景下，RAT 首先完成释放（包括收放作动器伸长并推动支撑臂展开、舱门打开）。释放到位后，冲压空气驱动涡轮旋转并工作。此时RAT涡轮会受到一个向后的气动推力。此外，舱门所受气动力也由舱门连杆传递给RAT。需要指出的是，整个工作过程中（直到迫降前），RAT 虽然也会承受过载和基础振动激励作用，但是这部分载荷与气动力相比可以忽略。综上，在工作场景下，RAT结构受到的载荷工况和相应约束如下：

(1) 展开工况。该工况下需要RAT 满足展开角度和舱门打开角度的约束。

(2) 气弹振动工况。气动力与结构刚度耦合导致的结构振动。RAT 在该工况下需满足涡轮处的转角位移约束。

(3) 静力工况。RAT 结构在舱门和涡轮气动力作用下需满足强度要求。

2 约束的数学建模

2.1 展开工况

RAT 展开过程类似于一种活塞连杆运动。根据图1(b)的RAT 拓扑结构图建立如图2(a)所示的多体运动模型。该模型中，考虑了收放作动器与支撑臂的连接点、收放作动器与舱门连杆的连接点并不在支撑臂轴线的实际设计情况。

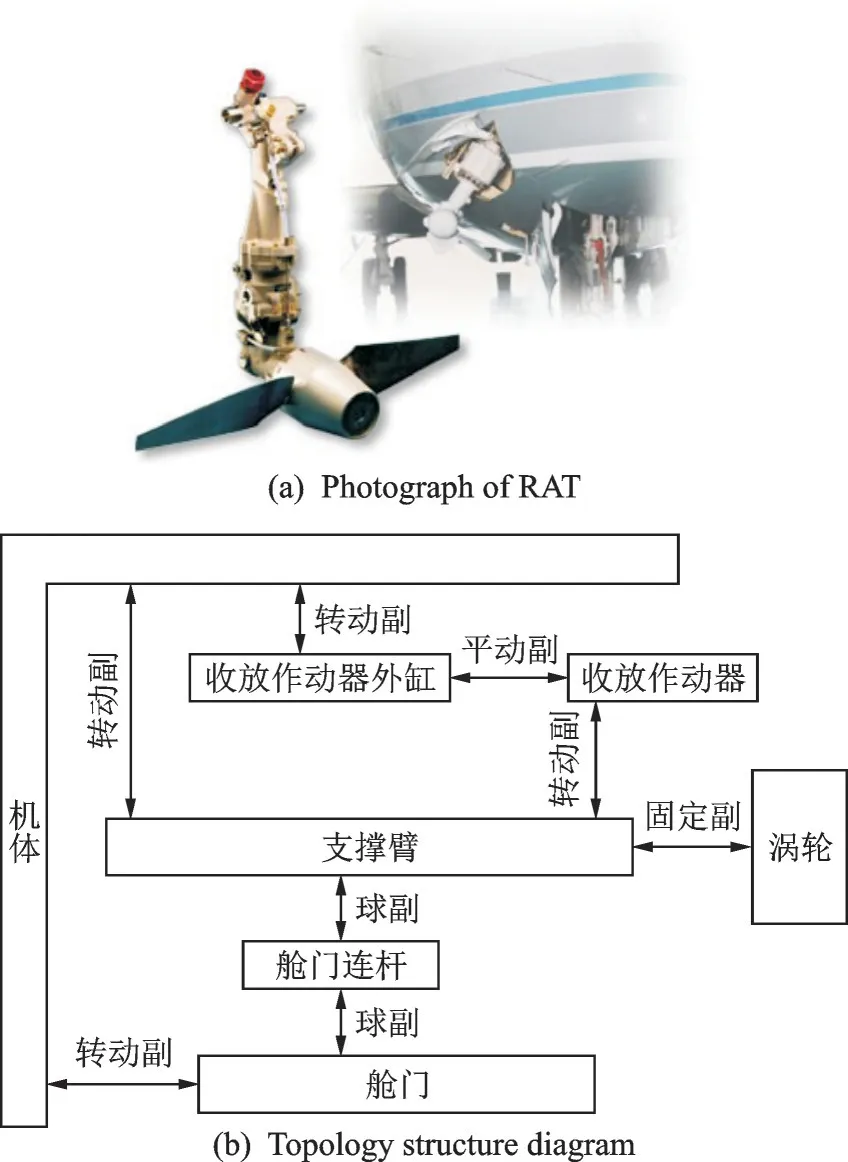
图1 RAT 实物图和相应的拓扑结构图Fig.1 Photograph and topology structure diagram of RAT

图2(a)中，连杆AC0是液压作动器，A点是作动器转动铰轴心，C0点是作动器与支撑臂的转动铰，过作动器AC0作支撑臂的垂线，垂足是C2点；连杆BH为支撑臂，B点是支撑臂与机体的转动铰；D1E0是舱门连杆，支撑臂和舱门连杆的球铰是D1点，D0是D1在支撑臂BH轴线上的垂足，E0点是舱门连杆与舱门的球铰；FG是舱门转轴，过球铰E0作舱门转轴FG的垂线，E1是垂足。由于机上结构的限制，图2(a)中的A、B、E0点位置和支撑臂长度BH均为已知量。

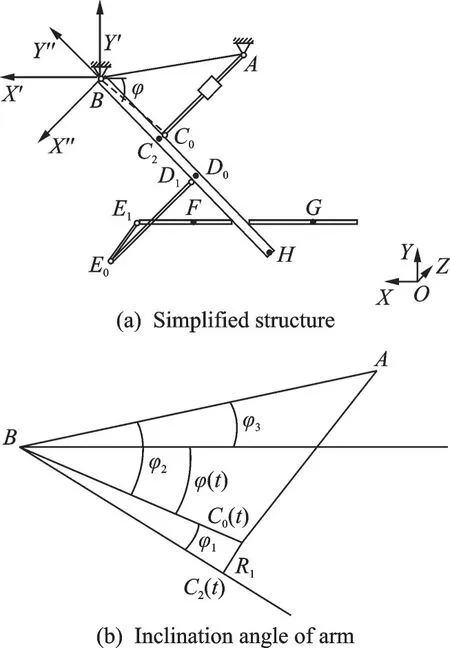
图2 结构简化模型Fig.2 Simplified structure model of RAT

在任意时刻t，支撑臂转轴B、收放作动器上转轴A、收放作动器与支撑臂连接点C0的位置如图2(b)所示。此时，收放作动器伸长了dl，长度为AC0+dl(t)。

对于图2(b)的直角三角形BC0(t)C2(t)，R1是C0(t)与支撑臂轴线的距离，则BC0(t)与BC2(t)的夹角为

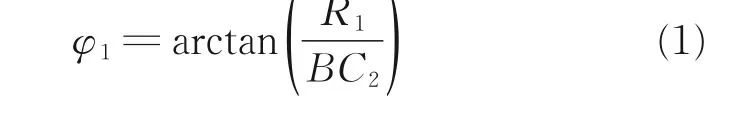
对于△ABC0(t)，AB与BC0(t)的夹角φ2随作动器AC0的伸长发生变化，由余弦定理得

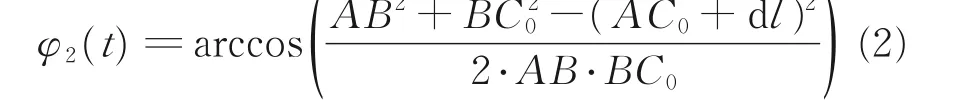
此外，φ3是AB与水平轴的夹角，由A、B两点的坐标确定。综上，任意时刻支撑臂展开角φ为

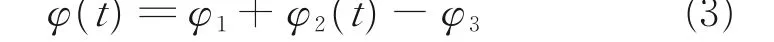
于是，C0、D1、支撑臂端点H在任意时刻t时的坐标可以通过矩阵变换得到。以C0为例，其任意时刻t时的坐标为

2.2 静力工况

无论RAT 处于贮存场景还是工作场景，均可基于构件三维空间位置分析各部件受力。简化起见，本文将舱门气动力、过载力都折算为绕舱门转轴的力矩MDoor。于是，舱门连杆的轴向力FE0D1按式(7)得到。

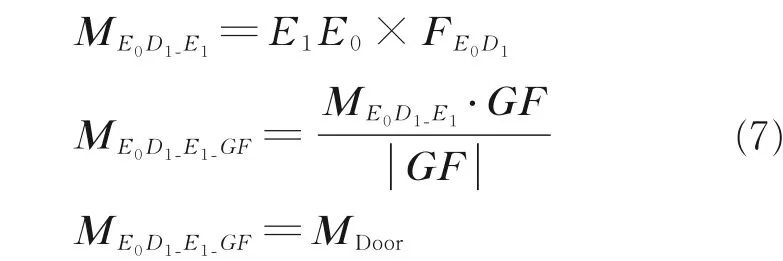
式中：FE0D1为舱门连杆的轴向力矢量，方向由E0指向D1；E1E0为 由E1指 向E0的 方 向 向 量，ME0D1_E1为舱门连杆的轴向力FE0D1相对E点的点之矩；GF为舱门转轴方向向量；ME0D1_E1_GF为FE0D1相对舱门转轴的力矩。类似地，可以计算得到收放作动器的轴向力和支撑臂上的轴向力、弯矩、扭矩。

各部件在结构方案设计阶段通常基于材料力学公式来估算应力水平。因此，本文将舱门连杆和收放作动器简化为圆环截面的二力杆以校核其正应力；考虑到支撑臂同时承受轴向力、弯矩、扭矩的作用，本文基于多型产品的工程经验将其简化为圆环截面，并校核其Mises 等效应力。支撑臂的Mis⁃es 等效应力最大截面出现在末端B处或与收放作动器连接的C2处。

2.3 基础振动工况

由于RAT 系统在基础激励作用下的位移响应难以得到解析解，本文基于ANSYS Mechanical 将整个结构简化为如图3 所示的板杆单元。通过有限元分析，得到结构方案在基础激励作用下的涡轮部位位移响应。

图3 板杆单元模型Fig.3 Plate-bar finite element model of RAT

2.4 气弹振动工况

对于工作场景下的气弹振动激励，其原理如图4 所示。在初始时刻，涡轮受到的气动力为

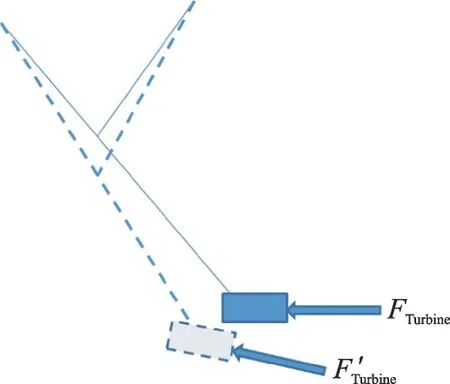
图4 气弹振动示意图Fig.4 Diagram of aeroelastic vibration of RAT

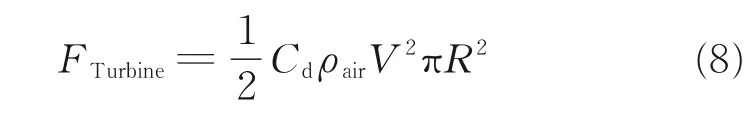
式中：Cd为推力系数，为与涡轮设计有关的常量；ρair为来流密度；R为涡轮半径，为与涡轮设计有关的常量；V为来流平行于涡轮轴线的速度。

RAT 受到FTurbine作用后产生向后的变形（设偏角为θ）。于是，来流平行于涡轮轴线的速度减小为Vcosθ，FTurbine相应地减小为F′Turbine，即

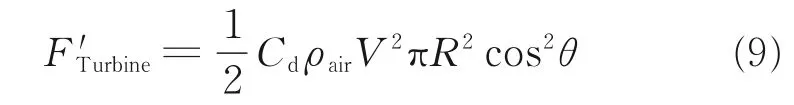
紧接着，RAT 结构的变形会减轻，从而又使F′Turbine增加。这样的波动往复产生，导致RAT 结构气弹振动。

综上，RAT 结构气弹振动的动力学方程为

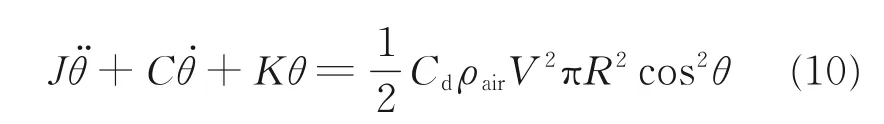
式中：J为RAT 结构弯曲转动惯量，由三维模型测量 得 到；C为RAT 弯 曲 阻 尼，取 工 程 经 验 值；K为RAT 结 构 弯 曲 刚 度，与BC2、R1、BD0、R2、θ1、RAC0_out、RAC0_in、RBH_out、RBH_in、RE0D1_out、RE0D1_in等 设计参数有关，本文通过ANSYS Workbench 软件分析得到。该振动方程是一个非线性常微分方程，难以有解析解。本文借助Amesim 软件进行数值求解。

3 优化模型

3.1 参数灵敏度分析

为了提高优化效率，快速找到对约束影响较大的设计变量，本文首先借助参数灵敏度分析进行优化参数筛选。某型RAT 系统的结构设计变量初始值如表1 所示。通过对表1 中的设计初始值施加1%的扰动，观察相关约束的变化情况。

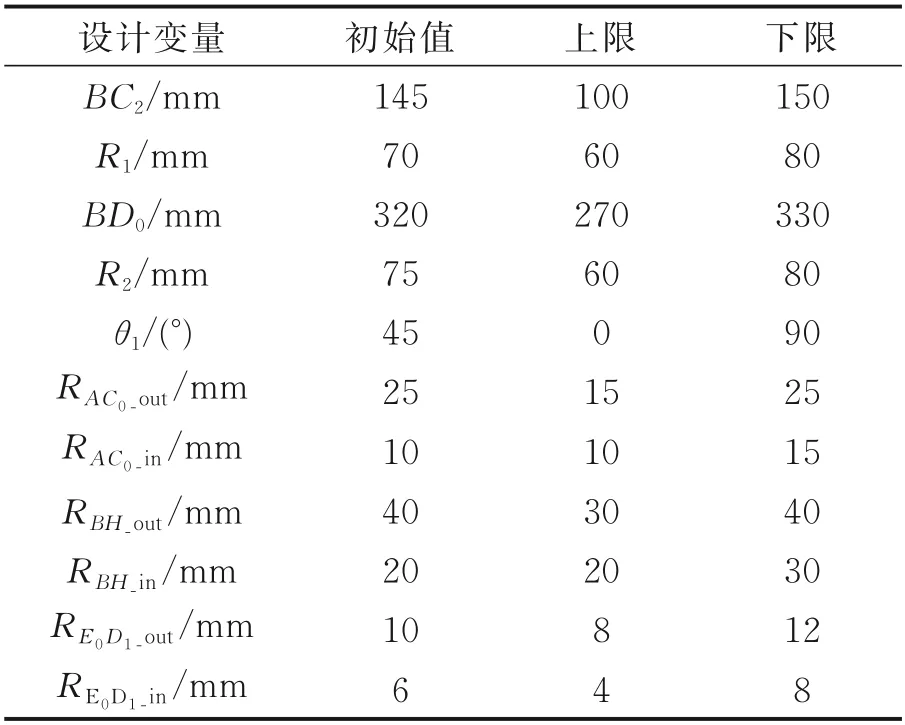
表1 设计变量初始值Table 1 Initial values of design variables

表2 是各设计变量对约束的灵敏度分析结果。表中：ψ为舱门转角，φ为支撑臂展开角，σE0D1为舱门连杆等效应力，σC0A为收放作动器等效应力，σBH为支撑臂等效应力，sH_base为基础激励下的涡轮位移响应，θH_air为涡轮处的气弹振动转角。

从表2 中可以发现，R1、R2、θ1这3 个变量对任意约束的敏感度均小于2%，因此在建立优化模型时忽略这3 个设计变量。换句话说，本文将舱门连杆、收放作动器与支撑臂的连接点简化到支撑臂轴线上。

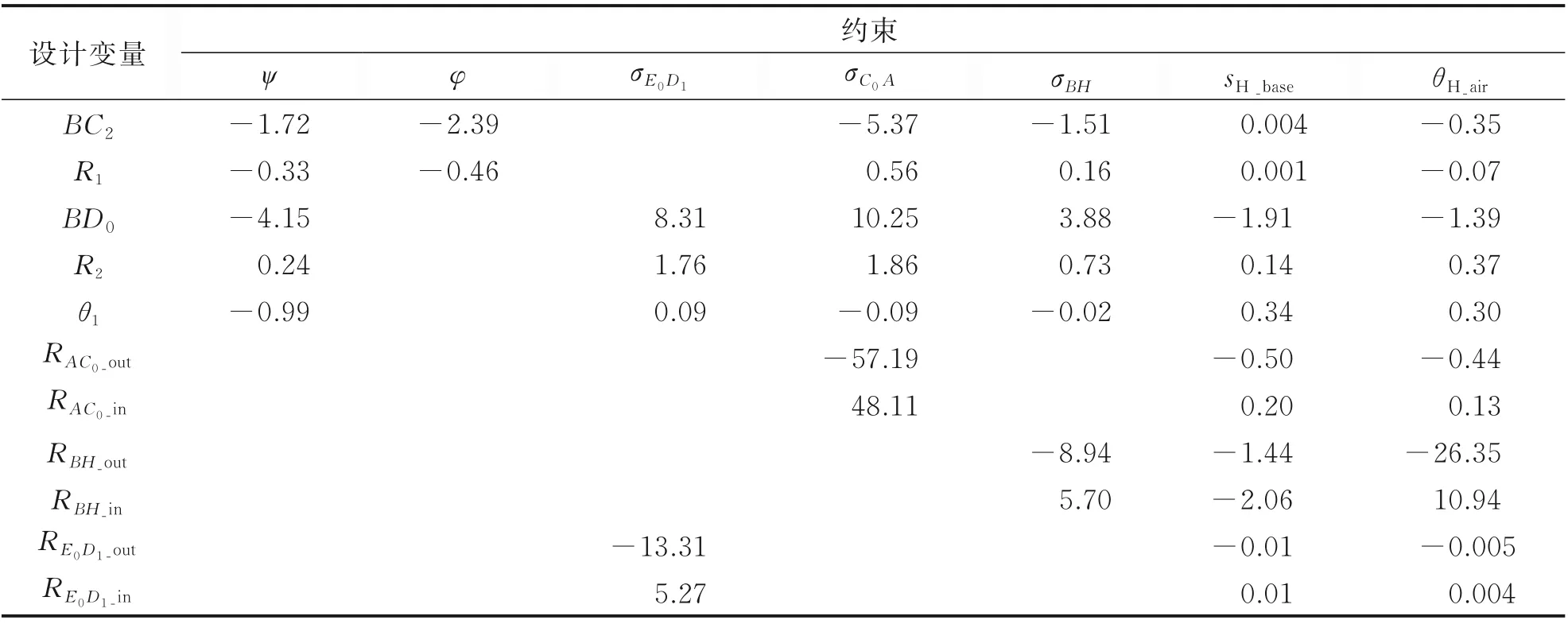
表2 灵敏度分析结果Table 2 Results of sensitivity analysis %

3.2 优化模型

协同优化方法（Collaborative optimization，CO）是针对航空器不同学科间组织和通讯困难问题而提出的一种两级多学科优化方法。CO 法在系统级负责从全局考虑优化设计变量和各子系统间的耦合，并通过一致性约束协调各子系统设计之间的差异；在各个子系统层级，则分别独立优化相应的设计变量，使在满足子系统级约束条件下与系统级指定的全局设计变量之间的差异最小。

本文所研究的RAT 结构在贮存场景和工作场景下分别处于回收、展开构型，结构差异较大，且两种场景下的约束条件也不同。与此同时，两种场景下的结构设计变量却又相同。因此，这类RAT 结构优化问题非常适合采用CO 法进行求解。

采用动态松弛CO 法构建优化模型如下。

系统级优化模型

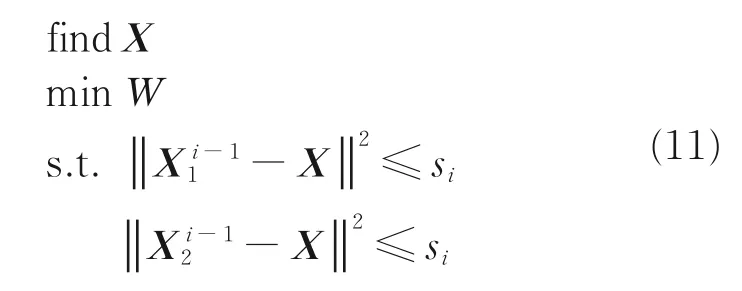
动态松弛因子能够动态调整系统级优化变量与子系统级优化结果的差异，保证系统级协调优化的速度和收敛性。式（12）中，λ本文取0.7，Δi为第i轮系统协调时的子系统间不一致信息，定义为

贮存场景子系统级优化模型

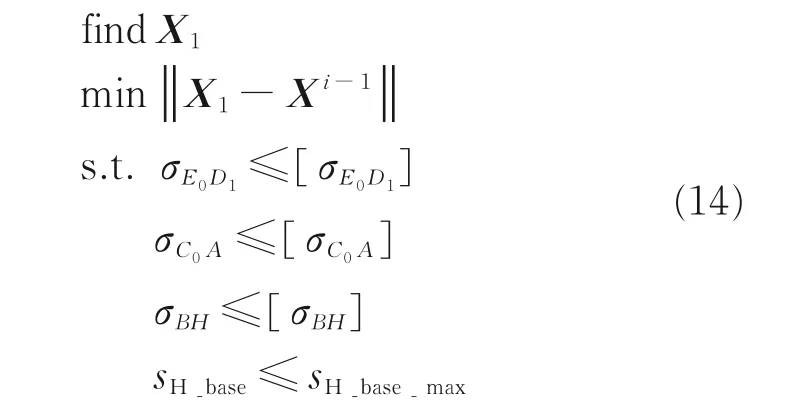
式中：X1为贮存场景的子系统级优化变量矩阵；约束σE0D1为舱门连杆等效应力，不大于600 MPa；约束σC0A为收放作动器等效应力，不大于600 MPa；约束σBH为支撑臂等效应力最大值，不大于400 MPa；约束sH_base为基础振动激励下的支撑臂端部H点位移量，不大于2.5 mm。Xi-1为前一轮系统协调后的优化变量值，该子系统级优化目标是使X1与Xi-1的距离最小。

工作场景子系统级优化模型

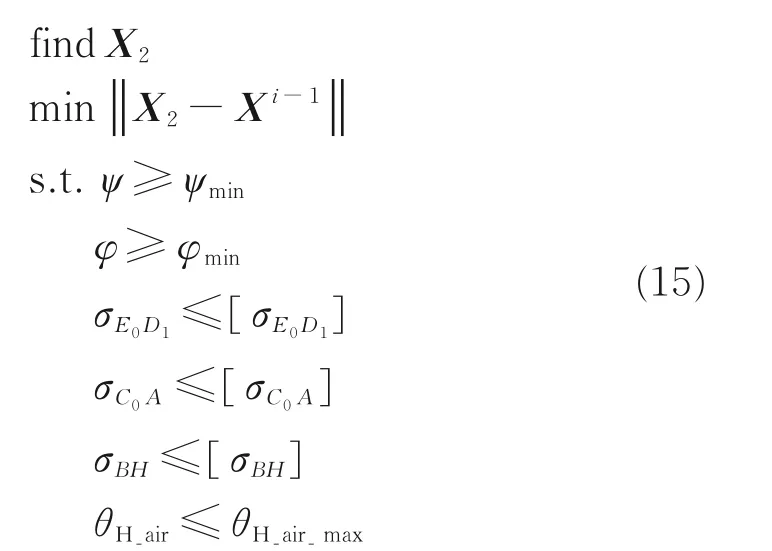
式中：X2为工作场景的子系统级优化变量矩阵；约束ψ为舱门展开角度，不小于110°；约束φ为支撑臂展开角度，不小于85°；约束σE0D1为舱门连杆等效应力，不大于600 MPa；约束σC0A为收放作动器等效应力，不大于600 MPa；约束σBH为支撑臂等效应力最大值，不大于400 MPa；约束θH_air为气弹振动下的涡轮处角位移，不大于8°。与贮存场景类似，本子系统级优化目标是使X2与Xi-1的距离最小。

3.3 优化结果

本文采用多学科优化软件Isight 集成Matlab、Amesim、ANSYS Workbench 搭建优化流程如图5所示。在Matlab 中计算舱门展开角、支撑臂展开角、贮存和工作场景下的部件位置和强度；在AN⁃SYS Workbench 中基于Matlab 计算得到各部件位置建立有限元模型，计算贮存场景中基础振动下的端部振动位移和展开后的结构弯曲刚度；在Ames⁃im 中基于结构弯曲刚度进行工作场景中气弹振动工况下的涡轮转角计算。优化目标W为RAT 结构重量，为设计变量的经验函数。

经计算，优化结果如表3 所示。可以发现，基于动态松弛的协同优化算法将RAT 系统的结构重量优化至初始重量的87%，相对模型初始值减小13%。该组优化结果在系统级、贮存场景、工作场景优化模型中能够同时满足约束条件。

4 结 论

本文针对RAT 系统进行了结构载荷分析和约束建模，基于协同优化方法建立了结构多工况优化模型并进行了优化算例求解。本文主要结论如下：

(1) RAT 系统在贮存场景下主要承受基础振动和舱门气动吸力的作用；在工作场景下主要承受涡轮气动推力和舱门气动力的作用。RAT 系统在工作场景下需要考虑气弹振动约束和展开位移约束。相关强度、位移、气弹约束可以借助刚体动力学、结构力学、仿真等方法建立数学模型。

(2) 通过敏感性分析可以识别RAT 结构方案设计中的关键设计变量为支撑臂、收放作动器、舱门连杆的内外径以及它们之间的连接点位置。

(3) 基于动态松弛CO 法，可以建立考虑多场景、多约束的RAT 结构优化模型。该优化模型通过约束不同场景间的不一致信息，最终得到全局最优设计。针对某型RAT 系统，本文基于该优化模型将结构重量优化至初始重量的87%，优化效果显著。