基于深度学习的期末复习教学实践与探索

蒋瑾鑫

[摘  要] 把握数学知识的本质，建立知识架构，把握知识间的相互联系，挖掘数学思想，只有这样，学生才能灵活迁移，实现深度学习结合理论研究和复习教学实践. 文章以七年级上册复习教学为例，提出指向深度学习的期末复习策略，即追根求源，明晰概念;深度思考，掌握方法;知识整合，前后贯通.

[关键词] 深度学习;期末复习;初中数学

在传统的期末复习课中，部分教师罗列知识点，然后做习题;部分教师只做题，然后根据学生错误讲解错题，走的是整章复习、期中复习的老路. 由于教师对复习的原因、复习的内容、复习的方法缺乏深入的思考，复习效果可想而知. 从掌握知识的整个过程来看，新授课是积累零散的知识，所学知识由薄变厚;复习课是将知识进行系统的梳理与比较，让所学知识由厚变薄. 但期末复习与平时复习有所不同，期末复习时间较长，内容多跨度大，学生需要对所学知识融会贯通，这就需要教师要把握数学知识的本质，建立知识架构，把握知识间的相互联系，挖掘数学思想，只有这样，学生才能灵活迁移，实现深度学习[1]. 基于此，笔者结合理论研究和复习教学实践，以七年级上册期末复习教学为例，提出指向深度学习的期末复习策略，期望能够起到抛砖引玉之效果.

追根求源，明晰概念

七年级上册的教学内容衔接了小学与初中的数学知识，学生在小学数学里学习的数学知识是非负数的运算，各种计量单位及相互关系，认识基本图形及它们的周长、面积与体积计算等. 初中阶段的数学学习，学生要由直观学习过渡到抽象学习，学生要建立数感与符号观念，发展运算能力与推理能力. 虽然经过了半年的数学学习，但是学生的记忆仍然比较简单，推理不够严密，思考比较直接，知识不够系统，为此，对知识的回顾是必要的. 但只回顾知识点，学生的回忆过于简单，如果通过做题激活学生的知识，让学生主动地回忆知识，复习效果会更好.

案例1  教材第5章第2节“垂线”.

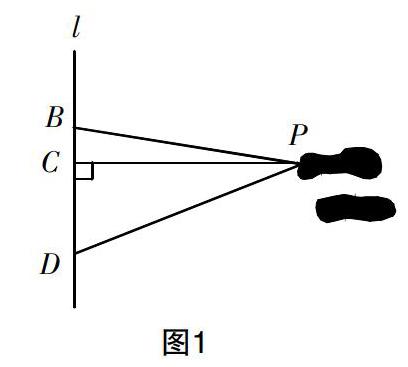
在体育课上，某一同学立定跳远的情况如图1所示，l表示起跳线，在测量该同学的实际立定跳远成绩时，应测量图中线段PC的长，理由是__________.

对于此题，有部分学生答“两点之间，线段最短”，其理由是：该学生的起跳处是一个点，落脚处也是一个点. 这反映了学生知识点记忆很好，但却不能把知识点与应用场景相对应，把相似或相近的知识点混淆了. 此时，需要追本求源，梳理知识的来龙去脉. 基于此，笔者做出如下引导——

教师：题中PC的长就是一个距离，我们已经学过的距离有哪些？它们是如何定义的？

学生：我们学过的距离有两种，一是两点之间的距离;二是点到直线的距离，两点间的距离是用它们之间线段的长进行定义的，点到直线的距离是用它们之间垂线段的长进行定义的.

教师：为什么这样定义呢？

学生：因为两点之间，线段最短;点与直线之间，垂线段最短.

教师：要求两处之间的距离，通常把这两处抽象为两个点，也就是求两点之间的距离，而此题是求谁与谁之间的距离，如何抽象？

学生：脚的位置就是一个点，起跳线就是一条直线，所以PC的长就是点P到直线l的距离.

教师：既然PC的长是点到直线的距离，而定义点到直线距离的原因是垂线段最短，所以本题的理由就是垂线段最短.

建立知识间的相互联系，深刻理解概念，才能把实际问题正确抽象出来. 在基础知识的复习教学中，教师要启发学生自主探索，回归本源，寻找知识的本源，把实际问题抽象为几何图形，不断发展学生的空间观念，提高学生解决实际问题的能力.

深度思考，掌握方法

知识点的回忆是复习不可忽视的环节. 对于较难的数学问题，重要的不是得到问题的答案，而是如何得到问题的答案，以及在解决问题的过程中，如何运用所学知识？如何切入问题？解决的策略是什么？这些才是教师教学的重点. 知识点是显而易见的，但知识背后的生成过程却是宝贵的，教师要回归课本，找到知识发源地，重温知识与方法的生成过程[2].

案例2  教材第四章第6节“角”.

图2是一副特制的三角板，用它们可以画出一些特殊角.在下列选项中，不能画出的角度是（    ）

A. 18°？摇？摇 B. 44°？摇？摇C. 96°？摇？摇？摇D. 114°

学生对于此题毫无头绪，此时，笔者要求学生重温课本，一起回顾：如何利用一副三角板画出一些角度？

学生：需要分类去寻找，用一个角，两个角相加或相减，三个角相加或相减，可以画出哪些角？

学生：用一副三角板的一个角画角可以画出30度、45度、60度、90度;用两个角的和或差画角可以画出15度、75度、105度、150度;用三个角的和或差画角可以画出135度、165度.

教师：同学们，一共能画出多少个角呢？这些角中最小角度與最大角度分别是多少？你发现这些角有什么共同特征吗？

学生：一共可以画出11个角，最小角度是15度，最大角度是165度，这些角都是15的倍数.

教师：那么用这副特制的三角板画角，可以画出哪些角度？这些角度的共同特征是什么？

学生：用这副特制的三角板画角，可以画出30度、60度、36度、72度、66度、6度、144度、108度等，这些角度都是6的倍数.

教师：请同学们自行解决这道题.

深度思考的特征就是运用联想寻找数学活动经验，运用类比的方法进行方法迁移，让欲求问题与已有经验相联系，与课本知识相联系，这样会使学生的想法合理，解法自然，注重知识与经验的积累，将课本的方法进行本质概括和合理迁移，让深度学习真实发生.

知识整合，前后贯通

在期末复习中，要把散乱的知识进行合理的整合，按知识的相同或相似点进行整合，也可以将不同模块的数学对象根据其发展脉络串联，让分析与比较、综合与评价这些高阶思维参与到深度学习中来[3]. 人的大脑分为左、右两个半球，其分工不同，一边负责形象思维，另一边负责抽象思维，它恰好反映了客观世界的数与形，而数学中的代数主要用来训练人的抽象思维，几何主要用来训练人的形象思维，这两种科学的思维工具既有区别也有联系. 在七年级上册的教学中，数轴将数与形进行了有机结合，为此，笔者设计了直线上的动点问题，实现了数与形的完美结合.

案例3  如图3，已知数轴上点A，O，B对应的数分别为-2，0，6，点P是数轴上的一个动点.

（1）设点P对应的数为x. ①若点P到点A和点B的距离相等，则x的值是_______;②若点P在点A的左侧，则PA=_______，PB=_________（用含x的式子表示）;

（2）若点P以每秒1个单位长度的速度从点O向右运动，同时点A以每秒3个单位长度的速度向左运动，点B以每秒12个单位长度的速度向右运动，在运动过程中，点M和点N分别是AP和OB的中点，设运动时间为t.①求MN的长（用含t的式子表示）;②当t=5时，请直接写出的值.

教师：点P到点A，B的距离相等，表明点P是什么？

学生：点P是线段AB的中点.

学生：根据中点坐标公式，可得x=（-2+6）÷2=2.

教师：当点P在点A左侧时，说明了什么？

学生：说明x<-2，x<6.

学生：根据两点距离公式，得PA= -2-x，PB=6-x.

教师：移动后，点A、点B、点P在数轴上所表示的数是什么？

学生：点A表示的为-2-3t，点B表示的数为6+12t，点P表示的数为t.

教师：根据点M是AP的中点，点N是OB的中点，点M、点N表示的数分别是什么？

学生：点M在数轴上所表示的数为（-2-3t+t）÷2=-1-t;点N在数轴上所表示的数为（6+12t+0）÷2=3+6t.

学生：MN=3+6t-（-1-t）=4+7t.

学生：当t=5时，

数轴与坐标系实现了代数与几何的有机结合，通过分析，学生对此有了深刻的理解与体验，经过综合题的训练，学生开阔了视野，发展了高阶思维能力. 学生学习的知识是零散杂乱的，教师设计学习活动，调动学生的活动经验，促使学生进行整合、联想，实现了前后知识的整合与贯通，促进了学生的深度学习.

总之，教材是学生学习的重要依据，也是教师教学的重要素材，在期末复習中，教师要引导学生回归课本，引领学生反复品读课本，在追根求源中明晰概念，在深度思考中掌握方法，在知识整合中实现前后贯通，进而促进学生的深度学习.

参考文献：

[1]王磊. 搭建框架，促进学生深度学习[J]. 中学数学教学参考，2020（27）.

[2]吕亚军. 深度学习视阈下的初中数学课堂教学策略探析——一节省级重点课题研讨课引发的思考[J]. 中学数学月刊，2020（03）.

[3]张永才. 以“有理数的减法”为例谈如何进行深度学习[J]. 中学数学月刊，2019（02）.