关于“乘法分配律”有效教学的实践与思考
陈建伟


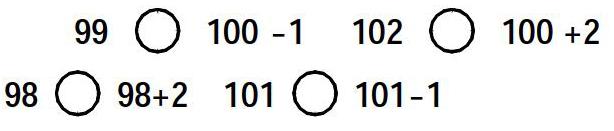
[摘 要] 学生从四年级开始系统学习运用运算定律进行简便计算,对于简便计算,绝大部分学生是相当乐意学习的,因为它在很大程度上降低了计算难度,使计算变得更为简单、轻松;但是对于乘法分配律的应用,却有较多的学生经常犯错,究其原因是学生对于乘法分配律的理解不够全面,往往停留在字面上、格式上的认识,没有真正感悟到乘法分配律算理的内在成因,最终导致错误的出现。因此如何帮助学生深刻理解乘法分配律,就成为一个极其重要的问题。文章结合学生在使用乘法分配律时常见的错误,谈谈教学中如何纠错和预防,以消除学生学习上的误区,使其真正理解乘法分配律,并利用好这一运算定律。
[关键词] 乘法分配律;有效教学;常见错误;错因;解决策略
人教版小学数学四年级教科书对乘法分配律的定义为:“两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。”用字母表示为(a+b)×c=ac+bc。实际教学中发现:学生通过对定义的字面理解和对字母公式的记忆,能够完成简单的应用。下面结合实际教学中的常见问题,谈谈笔者的几点思考。
一、借助情境解决学生片面理解定义而产生的错误
错例1的错因:学生没有认识定义中“先把它们与这个数分别相乘”的“分别”,即两个数都要与括号外面这个数相乘,否则出现漏乘现象,产生“分配不公”。
针对这类错误,教师可结合买服装的情境,让学生理解存在“不公”的地方在哪里,应如何避免“不公”的出现。如“一件上衣25元,一条裤子7元,裤子和上衣各买4件,共需多少钱?”列式(25+7)×4,就是先求一套服装的价钱,再求出4套服装的价钱;而25×4+7就是先求4件上衣的价钱,再加上一条裤子的价钱,这样就不是求4件上衣和4条裤子的价钱了。学生通过这样实际的对比,就能清楚地知道裤子只买了一条,所以不对,应该把7也乘4才合理。这时教师要紧接着再次出示定义,并重点解释“分别”二字的意义,从而让学生了解定义。此外,教师可在新课教学时就有针对性地设计此类错误的展示,并组织学生展开讨论,让学生自己发现问题,并能合作解决问题,这样才能从根本上杜绝此类错误的产生。
错例2的错因:学生过分在意乘法分配律名称中的“分配”了,将括号外的数也进行了拆分,也可能是受教师在纠正错例1中“分配不公”的影响,出现了“过度分配”。
要帮助学生认识此类错误,也可结合买服装的情境进行解释,但是要避免此类错误的发生,要求教师在解释乘法分配律定义时应让学生说说分配律是如何分配的,把谁分配给谁,然后结合具体的情境帮助学生理解定义中“与这个数相乘”的“这个数”是哪个数、为什么。如在买服装的情境中,可以让学生明白买4套服装可以用“一套服装的价钱×4”,即(25+7)×4;而不是上衣和裤子各买2件,即25×2+7×2。通过这样的情境,学生可以轻松地认识到(25+7)×4=25×4+7×4。
错例3错因:由于过分强调乘法分配律的定义内容,学生一见到两个数的和乘一个数,就机械式地使用运算定律进行“简算”,虽然答案正确,但由于忽视了题目实际的需要,反而“不切实际”。
要避免此类现象的发生,需要教师在使用运算定律进行简算的初始阶段,让学生明确简便计算的目的,不能颠倒问题本质,产生因定律而定律的现象。作为教师,在教学时不能一味要求学生记忆定律或公式,应重视结合具体情境,帮助学生了解定律的算理和应用的目的及范围。
总之,乘法分配律的教学与实际情境相结合,有利于学生理解运算定律的算理;教师在结合情境进行教学时,也应注意将定律从情境中抽离出来,进一步巩固定义,将定义应用到其他情境中。如此,可避免学生在一种情境中固化地理解乘法分配律,而是将其更广泛地运用到其他实际问题。
二、预先铺垫解决学生片面重视“简便”二字而产生的错误
错因:在简便计算的过程中,学生对于“凑整”的方法记忆深刻,过分追求“简”,而忽略了計算的基本——运算顺序,一次次地被“百(100)骗而不厌”。
对于这类错例,教师可以尝试这么做:
第一,在练习课前,先伏笔地进行铺垫练习。如比较下面式子的大小:
练习后,再出示56×99,并提醒如何凑整才不会改变算式的大小,这样学生通过之前的铺垫练习,就能懂得99应改成100-1,例1的错误就不会再发生了。
第二,在练习课中,再进行针对性的对比练习。如判断对错,并说明理由:
(1)28×99+28×1 (2)28×99+28
=28×(99+1) =28×(99+1)
=28×100 =28×100
=2800 =2800
(3)28×99+1
=28×(99+1)
=28×100
=2800
对于第(1)题,应让学生说说为什么对,理由是什么。要让学生试着说出这是乘法分配律的逆应用,即“两个数同时乘上同一个数后相加,可以先把这两个数先相加,再把和与那个数相乘,结果不变”。
对于第(2)题,要让学生明白加号后面的28可以看成是28×1,这样就是第(1)题了,因此也是对的;但是这里要让学生明白为什么可以在28后面加上“×1”,这是因为根据运算顺序先算28×1得28,这样本题修改后的计算结果与原题是一样的,因此可以加上“×1”。
对于第(3)题,可以放手让学生辩论,教师负责在最后做一个小结:解题应有理有据,前面两题是根据乘法分配律的逆应用而加括号简算的;第(3)题没有根据加了一个括号,使得计算变得简单,但是却因为无理地改变了原题的运算,导致计算结果出现错误,这是不允许的。
练习后教师可再次强调,简便是建立在“有理”的基础之上的,若仅仅为了简便而“无理”地简化了计算,终将导致结果的错误,这是不可取的。
三、对比练习解决学生各种运算定律混淆而产生的错误
错例1和错例2的错因:学生对运算律的理解停留在“公式化”“格式化”的基础之上,片面关注“括号”,一看到“括号”就自觉地进行分配,学完乘法分配律,就将乘法结合律抛之脑后,犯了“只认分配,不认结合”的错误。
解决这一问题的方法,也可以使用对比区分。如在练习课中出示:(1)8×(4×125);(2)8×(4+125);(3)8×4+8×125。这三道算式,让学生不计算就判断哪些算式的结果相等,为什么。
学生通过分析就可以清楚发现(1)(2)两题的明显区别,同时学生在说明原因的过程中,将会对乘法分配律定义中的“两个数的和”有更深刻的认识,同时对于乘法结合律也能准确应用。这样以后在应用乘法分配律时就不会犯这样的错误了。
错例3的错因:学生犯这样的错误,一方面是受到“凑百”的影响,另一方面是学生勇于探究,自发将乘法分配律过渡成“除法分配律”,自创一个实际并不存在的定律。
对于这类问题,教师应表扬学生的创新能力和探索精神,虽然结果是错误的,可是应从中看到学生的思维灵巧性,应该给予支持,并鼓励学生探索“除法是不是不能分配”,使学生认识到(a+b)÷c可以分配成a÷c+b÷c,至于其中的道理,师生可以在小范围内共同探讨。
总之,我们的教学不应仅仅要求学生了解运算律,更为重要的是希望学生能通过探索与思考,真正理解运算律的算理。因此,教师在教学乘法分配律时,应在整个教学过程中充分考虑学生的个体实际,并在新课教学时,设计结合学生的生活实际的情境,让学生不知不觉应用乘法分配律去解决实际问题;在练习课时也应重视设计对比练习,引发学生探索与讨论,使学生能够真正掌握运算定律,而不是公式化记忆和格式化应用。

