基于动态交易和风险约束的智能投资组合优化

王舞宇 章 宁 范 丹 王 熙

一、引言

投资组合管理是一个十分复杂的非结构化决策过程，涉及金融预测、投资决策分析、组合优化等一系列过程，受到宏观经济、投资者心理、政府政策等多方面的影响(Paiva等，2019[1]；赵丹丹和丁建臣，2019[2])。随着金融市场的不断变化，市场上的金融资产信息也在发生着改变，投资者不仅要对已持有的投资组合内部资产进行调整，还需要结合市场状况来决定买进市场上的哪些资产同时卖出投资组合中的哪些资产，以实现投资效用的最大化。根据适应性市场假说理论，金融市场是一个复杂的动态系统，任何单一的优化方法都不可能永久获益，随着市场的有效性逐渐提高，一些模型的获利机会就会消失，也许在某一段时期模型A表现较好，而在另一段时期模型B表现更好，难以保证投资者的利益最大化。有效的投资组合模型应该在感知市场状态变化的同时，进行适应性的调整并采取相应的资产交易行动，以更好地服务于投资组合管理(梁天新等，2019[3])。

随着金融大数据的发展，巨大的数据量对数据存储、数据分析和计算技术都提出了更高的要求(黄乃静和于明哲，2018[4])，这无疑增加了投资组合管理相关研究的难度。传统的统计学方法并不适合用于分析复杂、高维度、具有噪音的金融市场数据序列，因为统计学分析往往基于有大量约束的条件进行建模，而且这些假设在现实生活中往往不能完全成立，所以模型结果受到了前提条件的限制(Längkvist等，2014[5])。而早期的机器学习方法的表现在很大程度上依赖于人工特征设计，这将会对结果造成一定的干扰，无法对复杂的金融数据进行准确建模(Wang等，2020[6])。近几年，基于机器学习的人工智能系列方法的出现为以上问题提供了新的思路。其中，强化学习是机器学习领域的一种比较前沿的方法，与监督学习不同，它并不仅仅依靠已知的、固定的数据进行学习，而是在不断变化的外界环境中，通过大量、多次的试错学习，寻找到产生最佳结果的路径(Park等，2019[7])。

因此，本研究将采用强化学习提出一种基于动态交易的智能投资组合优化方法。与以往研究相比，本研究所提出的方法主要有以下两点优势：第一，在投资组合的管理过程中，不仅考虑了资产本身信息，还考虑了外部市场环境对投资组合管理过程的影响，能够依据当前市场状态和资产信息自动转换投资组合优化模式，以应对不同的市场风格变化；第二，投资者可以依据自己的投资风险偏好来选择相应的目标函数，根据目标函数最大化原则，通过投资组合内部资产与外部资产池动态交易的形式，来实时调整投资组合资产构成及资产配置。也就是说，本研究中的投资组合优化不再局限于投资组合内部资产配置的调整，而是能够根据市场状态、资产信息、投资者风险偏好来实时更新资产构成和相应的投资比例。

二、文献综述

随着智能时代的来临以及金融数据分析需求的提升，利用计算机进行自我学习和大量计算，并实现投资组合的管理与优化已经成为可能，越来越多的学者开始将人工智能作为研究解决方案的支撑，并证明人工智能方法比传统的统计学模型能更好地处理非线性、非平稳特征问题。

目前在国内外关于智能投资组合优化研究中，很多学者采用传统的机器学习技术对金融财务数据或交易数据进行分类汇总进而建立模型来为投资者选择和优化投资组合，主要应用的方法包括：专家系统(Yunusoglu和Selim，2013[8])、支持向量机(Paiva等，2019[1])、进化算法(齐岳等，2015[9])、梯度下降(吴婉婷等，2019[10])、人工神经网络(Freitas等，2009[11])等。例如，Paiva等(2019)[1]结合支持向量机和均值方差模型两种方法进行了投资组合的优化研究，他们首先利用支持向量机对资产的收益变化趋势进行了分类，筛选出预测收益更高的一些资产作为投资组合的组成成分，再利用均值方差模型来优化投资组合，从而实现收益最大化的目标。此外，深度学习是机器学习中一种对数据进行表征学习的算法，由Hinton和Osidero(2006)[12]提出，它擅长处理复杂的高维数据，且不依赖任何先验知识和假设，是一种更加贴近实际金融市场数据特征的方法，也是推动智能金融的关键技术(苏治等，2017[13]；Chong等，2017[14])。深度学习在投资组合构建与优化中的应用非常少。目前只找到两篇这方面的研究，例如，Heaton等(2016)[15]基于经典的均值-方差理论(Markowitz，1952[16])和深度学习构建了一个深度资产组合理论，该理论首先基于深度自编码器对金融市场信息进行编码，然后再解码从而形成一个符合目标函数的资产组合，实验结果表明该投资组合的表现优于基准模型IBB指数的表现。Yun等(2020)[17]提出了一个两阶段的深度学习框架来训练投资组合管理模型，他们首先利用主成分分析对各个组的资产数据特征进行降维，然后根据市场指标将高度相关的资产分为同一组，针对每一组采用深度学习网络来建立一种预测模型，最后再次结合深度学习方法和均值方差模型对不同组的投资组合权重进行预测，从而构建并优化了投资组合。

强化学习方法侧重于提出解决问题的策略，可以通过多次试错来调整智能体行为从而找到最优结果(梁天新等，2019[3]；Khushi和Meng，2019[18])，具有决策能力，故强化学习方法在投资组合的构建与优化过程方面的应用相对比深度学习多，但文献数量仍十分有限。目前在投资组合优化领域应用较多的强化学习方法主要有四种。第一种方法是循环强化学习。Aboussalah和Lee(2020)[19]提出了一种层叠式深度动态循环强化学习架构，该方法能够捕捉最新的市场变化情况并重新平衡和优化投资组合，他们以S&P500不同板块的10只股票数据为研究样本，进行了20轮的训练和测试，实验结果表明采用他们提出的方法所优化后的投资组合实现了较好的市场表现。第二种方法是策略梯度方法。这是一种直接逼近的优化策略，直接在策略空间进行求解得到策略(梁天新等，2019[3])。Jiang等(2017)[20]运用强化学习中的梯度策略研究了加密货币中的投资组合优化问题，在该框架中，智能体(Agent)是在金融市场环境中执行操作的虚拟投资组合经理，环境包括加密货币市场上所有可用的资产及所有市场参与者投资组合的期望，投资组合的累计收益回报是奖励函数，通过将资金不断分配到不同的加密货币，获得更大累计收益，结果证明基于该方法提出的加密货币投资组合可以在50天内达到4倍的收益回报，明显优于传统的投资组合管理方法。第三种方法是Actor-Critic算法，又被称作“行动者-评论家”方法。例如，García-Galicia等(2019)[21]结合马尔可夫模型和强化学习中的Actor-Critic算法，提出了连续时间离散状态投资组合管理的强化学习模型，根据观察到的金融资产价格数据，每个状态的概率转移率和奖励矩阵构成了链结构的特征，并用于优化和确定投资组合中不同资产的权重，进而找到了波动率最低的投资组合。第四种方法是深度强化学习方法，即深度学习和强化学习方法的结合。Vo等(2019)[22]基于深度强化学习方法研究了社会责任投资组合的优化问题，这种组合把公司的环境、社交和治理三方面也考虑了进来。首先他们采用深度学习来预测股票收益，然后利用均值方差模型进行投资组合的优化，并基于强化学习对预测模型进行再训练，通过智能体的不断学习和参数调整，最终实现了投资组合的有效自主再平衡。

通过对相关文献梳理可知，以往相关研究存在以下两点不足：其一，大多研究是直接选定几种资产构建投资组合来优化投资组合，并未考虑外部市场资产池与投资组合内部资产动态交互的交易情景。随着金融市场的不断变化，市场上的金融资产信息也在发生着改变，投资者除了对已持有的投资组合内部固定资产进行调整外，还需要结合市场状况来决定买进市场上的哪些资产的同时卖出投资组合中的哪些资产，以实现投资效用的最大化。其二，已有研究大多忽视了投资过程中的风险因素，一般以收益率、累计收益率最大化作为投资组合优化的目标函数。但是这些纯收益指标无法体现出金融交易过程中发生的回撤情况。因此，有必要在投资组合优化的过程中考虑包含风险约束条件的目标函数以更好地应对市场风格变化。

三、研究方法及模型构建

(一)循环强化学习

循环强化学习算法(Recurrent Reinforcement Lea-rning,RRL)由Moody等(1998)[23]提出，是一种利用即时市场信息不断优化效用测度的随机梯度上升算法。RRL在自适应性上有一定的优势，易于根据当前金融信息自动转换交易风格,可以提供即时反馈来优化策略，能够自然地产生真实且有价值的行动或权重，而不依靠于值函数方法所需的离散化或者价格预测(梁天新等，2019[3])。RRL方法具有递归循环的特性，其核心思想在于当前时刻所采取的行动不仅仅与当前的市场环境有关，还依赖于前一时刻所采取的行动(司伟钰，2018)[24]。故循环强化学习在投资组合动态优化方面的研究具有较大优势。

(二)基于动态交易和风险约束的智能投资组合优化模型

1.算法更新规则。

本研究主要采用循环强化学习RRL为投资组合进行资产配置，同时生成多/空交易信号。为了让RRL方法能够应对金融交易市场的复杂变化情况，参考相关研究(Maringer和Ramtohul，2012[25]；Hamilton和Susmel，1994[26])的研究，我们将体制转换模型与循环强化学习方法相结合，提出了一种基于动态交易的自适应的智能投资组合优化方法(Ada-ptive Recurrent Reinforcement Learning，A+RRL)，该方法可以在不同的市场环境状态下选择不同的神经网络权重来应对市场风格的变化。

在金融市场，市场环境状态可以作为描述金融市场风格的重要标志之一(Aylward和Glen，2000[27]；曾志平等，2017[28])。参考吴淑娥等(2012)[29]对牛市和熊市的划分，我们以股票指数作为衡量市场状态变化的指标。我们将市场环境状态分为两类：牛市状态和熊市状态。具体来讲，这种双体制的循环强化学习模型可以描述如下：

Gt=[1+exp(-γ[qt-c])]-1

(1)

Ft=yt,1Gt+yt,2(1-Gt)

(2)

forj={1,2)

(3)

其中：公式(1)中的c表示体制转换阈值；γ决定了转换的平滑性；Gt代表不同的循环强化学习神经网络的权重，Gt∈[0,1]；qt为指示变量，其主要作用是让模型能够在熊市和牛市之间进行有效转换，以适应不同的市场状态。本研究选择股票价格指数的平均收益率作为指示变量qt的重要衡量指标。公式(2)中的yt,1和yt,2分别表示两个不同的循环强化学习神经网络。公式(3)中的rt为对数收益率，可以表示为rt=log(pricet/pricet-1)；wi,j代表对应的神经网络权重，即神经网络中不同单元之间连接的强度；v为神经网络的阈值。A+RRL模型可以被看作由两个RRL网络组成，每个网络对应着一种市场状态和交易风格并有一组独特的权重。而整个模型总输出为Ft，它是单个神经网络yt,1和yt,2的加权之和，权重主要受到指示变量qt的影响。A+RRL模型的结构如图1所示，该模型的每个网络对应一个独特的区域，在指标变量qt转换过程中，A+RRL可以在每个时间步选择合适的网络，以应对不同的市场风格变化。在此过程中，参数更新可以在每一次训练数据的前向传播过程中实现。

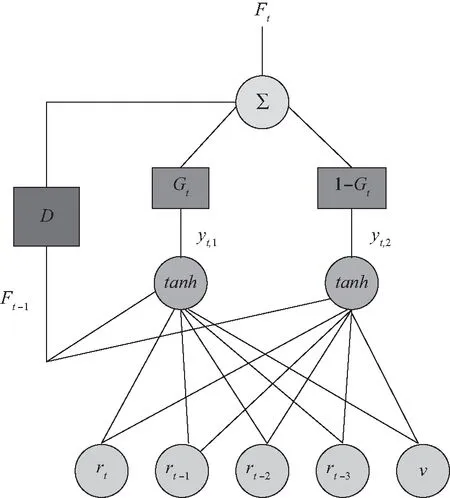
图1 自适应的循环强化学习模型

依据以上模型，我们将输出信息简写为Ft=tanh(x′tθ)，为交易信号，Ft∈{-1，1}；θ表示我们要训练的模型的一系列参数；xt为一个向量，可以表示为xt=[1;rt…rt-M;Ft-1]；M为要交易的时间序列，即交易周期。当Ft>0时，投资者将持有多头头寸，则设Ft=1；当Ft<0时，投资者将持有空头头寸，则设Ft=-1。rt为对数收益率，可以表示为rt=log(pricet/pricet-1)。持有的头寸在t时刻的回报如公式(4)所示，其中，μ为固定数值的资产数量，在本研究中表示能够交易的最大资产数量，δ为交易费用率。

Rt=μ×[Ft-1×rt-δ|Ft-Ft-1|]

(4)

给定交易信号Ft，模型将通过调整一系列参数θ来最大化目标函数UT。在给定的交易周期T内，目标函数UT对于参数θ的梯度更新的具体过程可以表示如下：

(5)

(6)

(7)

(8)

根据以上公式可知，dFt/dθ具有递归性质，依赖于前一时刻的动作。算法沿着梯度上升的方向θi+1=θi+ρdUT/dθ进行参数更新，可以将交易策略不断优化到目标函数的最大值,其中ρ为学习率。

为了让该模型可以用于投资组合优化而不单单是交易单支资产，当循环强化学习用于优化投资组合内部的资产权重配置时，我们设定fit=logsig(x′itθi)，其中，fit在时刻t对资产i的动作，这里指的是在不同时刻t对资产i的资产配置比例。logsig指的是log-sigmoid函数。于是我们可以得到以下公式：

(9)

最终模型的输出是投资组合中各个资产的配置权重：

Fit=softmax(fit)

(10)

值得说明的是，我们使用Ft=tanh(x′tθ)作为激活函数，从而得到每个资产在训练期间的交易信号，而fit=logsig(x′itθi)和公式(10)主要用于获得投资组合内资产的配置比例。在交易周期t，将投资组合资产i的交易信号Fit与相应资产i的投资配置比例wit结合，就可以得出每一交易周期的投资组合优化后的结果。由此我们可以得出：

(11)

2.目标函数。

不同的目标函数使得智能体学习的决策有所差异，从而导致投资组合优化结果也会有所不同。在大多投资组合优化研究中，目标函数均为投资组合的收益，并未考虑相应风险因素。然而，投资收益的增加必然伴随着风险的发生，故有必要将风险因素的约束条件纳入投资组合管理过程中，以满足不同投资者的投资需求。本研究从衡量投资组合绩效的指标中选取了两个比较常用且具有代表性的收益-风险综合指标，分别为夏普比率(Sharpe ratio)和卡玛比率(Calmar ratio)，作为目标函数。投资者可以根据个人偏好来自行选择相应的投资组合优化目标函数。微分形式为强化学习提供了一个非常有效的评估方法，有利于在强化学习模型训练的过程中直接优化RRL相应参数(Moody等，1998[23])。因此，在RRL模型部分，我们分别采用夏普比率和卡玛比率的微分形式作为目标函数，然后通过性能函数来增加模型在线学习过程的收敛性，并在实时交易中适应不断变化的市场状况。

(1)夏普比率。夏普比率是一个可以同时对收益与风险加以综合考虑的指标，表示的是单位风险收益，衡量的是投资的稳健性。夏普比率主要是为处理正向投资组合价值而设计的(Berutich等，2016[30])，也就是说，夏普比率将上涨和下跌的波动率视为同等位置。公式(12)表示的是T时间段内夏普比率ST，其中δ为交易成本，E[Rt]为平均收益率，σ[Rt]为收益率的标准差，γf为无风险利率。依据已有相关研究(Moody和Saffell，1999[31]；Almahdi和Yang，2017[32])，本研究设定γf=0。

(12)

微分夏普比可以看成是一个滑动平均式夏普比率，公式(13)至公式(15)展示了微分夏普比率的具体推导过程。

(13)

At=At-1+η(Rt-At-1)=At-1+ηΔAt

(14)

(15)

At和Bt分别表示收益率的一阶矩和二阶矩阵，微分夏普比率将移动平均值扩展为了自适应参数η的一阶展开。微分夏普比率DSAt表达式如公式(16)所示：

(16)

(2)卡玛比率。卡玛比率也是一种经过风险调整的投资组合绩效度量指标。它描述的是收益和最大回撤之间的关系，是一个最大回撤风险度量指标，度量从峰值到随后的底部的最大累积损失。与夏普比率不同，卡玛比率区分了波动的好坏，认为投资者更关心收益下跌时的波动率变化才是风险，因为收益上涨带来的高波动率符合投资者的投资需求，不应视作风险。可以发现，卡玛比率对投资损失比夏普比率更加敏感，故将卡玛比率作为目标函数有助于抵消市场长期下行风险(梁天新等，2019[3])。具体表示如公式(17)所示，其中，CalmarT为T时间周期内的卡玛比率，E[Rt]为T时间周期内收益率的平均值，E(MDD)是对应的期望最大回撤。参考Almahdi和Yang(2017)[32]的研究，微分卡玛比率可以表示为公式(18)至公式(21)。其中，γ为投资收益在一段时期的平均值，σ为投资收益在一段时期的标准差。

(17)

E(MDD)=

(18)

(19)

(20)

(21)

3.投资组合约束条件。

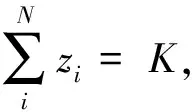
4.动态止损机制。

由于金融市场的复杂多变，金融交易中没有持久的确定性，所有的分析和预测只是一种可能性，根据这种可能性而进行的交易和投资行为自然会产生许多不确定性，因此有必要采取一些措施来控制相应的风险。已有研究表明，建立合理的动态止损机制在改善交易决策性能方面是有效的(Lo和Remorov，2017[34])。参考Almahdi和Yang的研究(2017)[32]，我们在每次交易决策的最后阶段加入动态止损机制，表示如下：

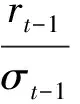
(22)

其中，rt-1为到时间点t-1的累计收益，而σt-1为到时间点t-1的累计收益的移动波动率，n为触发动态止损机制的波动日的天数。值得注意的是，该动态止损机制只应用于投资组合交易的测试阶段，而并不用于训练强化学习参数和模型。

5.投资组合动态优化过程。

在初始状态，投资者可以根据自己的偏好来选择想要实现的目标函数(夏普比率或者卡玛比率)。例如，如果投资者注重投资的稳健性，非常厌恶市场波动率，认为任何形式的波动都会给自己带来不利的影响，则可以选择夏普比率作为投资组合优化的目标函数；如果投资者更在意市场下行风险而不太在乎市场上行带来的波动，并对投资过程中的损失非常敏感，就可以选择卡玛比率作为目标函数。然后，我们需要考虑投资组合的基数约束，即对投资组合内部的资产数量约束。交易成本的改变也会影响我们模型的交易结果，在本研究中，将每次交易决策中的交易成本设定为固定不变的数值，为了更好地检验投资组合模型的稳健性，我们设定了多组交易成本。

接着是对模型进行系统训练，基于RRL方法，我们的智能体将持续监控和感知市场环境状态，根据目标函数和市场情况来从市场资产池中为投资组合动态挑选符合目标函数的资产，并进行投资组合资产权重的优化，然后再为投资组合中的每个资产生成相应的交易信号，从而产生多/空投资组合。在每一个交易周期T，投资组合内部资产与外部市场资产池都需要进行实时动态交易。也就是说，投资组合内部的资产构成及资产配置并不是固定不变的，而是随着交易周期T的推进以及市场与资产信息的实时变化而发生改变，以保证投资者所持有的投资组合能够实现目标函数最大化。值得说明的是，数据选择的范围可能会影响最后交易结果，故我们采用了一种多周期重叠式的投资组合交易训练方式来提升模型训练效率，训练窗口将在每次决策后向后逐步移动，以便每次训练都能够包含最新的市场数据。在模型参数选择方面，我们在输出层上采用了dropout正则化技术。它的工作原理为，在训练过程中，随机删除网络中的一些隐藏神经元，同时丢弃掉从该节点进出的连接，并保持输入输出神经元不变，然后将输入通过修改后的网络进行前向传播，将误差通过修改后的网络进行反向传播，以此来有效减少过拟合(Srivastava等，2014[35]；Fischer和Krauss，2018[36])。我们先采用部分样本进行了预实验，结果表明模型的性能会随着丢弃率(dropout ratio)的增加而下降，因此，我们将丢弃率设置为相对较低的0.1。然后我们采用应用较为广泛且有效的随机搜索法(Bergstra和Bengio，2012[37]；Greff等，2017[38])，根据上述设置动态地找到一个好的超参数组合。具体来讲，随机搜索对以下参数进行了采样：(1)学习率，范围从0到1；(2)epoch的个数，范围从100到5 000。其中，epoch指的是模型训练的迭代次数，1个epoch等于使用训练集中的全部样本训练一次；(3)每个资产的最大迭代次数，范围从10到2 000；(4)阈值c的大小，范围从0到2。最后我们选取了表现最好的一组数值作为参数集合，学习率为0.1，epoch为每个时间周期2 000次，每个资产的最大迭代数为100个，阈值为1。

此外，我们在每次交易之后加入了一个动态止损机制，如公式(22)所示。当投资组合的收益与风险比值达到了止损阈值，便会触发平仓止损操作，然后我们的模型将被重新迭代训练，模型参数将被更新，智能体将持续关注环境状态，等待下一次投资组合的建仓。如若投资组合的收益与风险比未能触发止损机制，交易将正常继续进行，每次交易将输出相应的奖赏值作为奖励，然后更新当前的交易信息存储到交易经验池中。通过这样的方式循环往复，直到投资期结束。为了更好地训练模型，动态止损机制只在测试阶段使用，并不应用于训练阶段。本研究所提出的带有动态止损机制的投资组合优化方法的具体过程如图2所示。

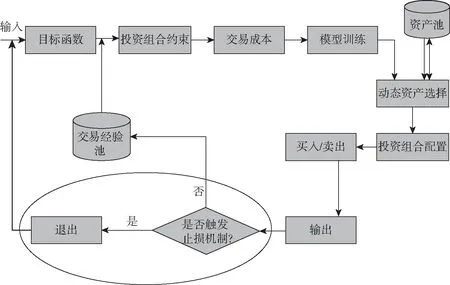
图2 基于动态交易和风险约束的投资组合优化过程(含动态止损机制)

6.基准策略。

基于本研究所提出的带有动态止损机制的Calmar/Sharpe+A+RRL模型，我们又选用了以下两种基准策略，用于同Calmar/Sharpe+A+RRL(Stop loss)模型在投资组合优化方面进行比较，以进一步验证模型的有效性。

(1)Calmar/Sharpe+A+DDPG(Stop loss)

不同的目标函数使得智能体学习的交易决策有所差异，从而导致交易结果也会有所不同。本研究选出了两个常用的衡量投资组合绩效的指标作为目标函数，分别为夏普比率和卡玛比率。保持模型的其他设置相同，通过不同目标函数的设定，来观察在不同的市场状态下哪种目标函数所搭配的优化模型可以带来更多投资收益。同时我们也可以保持相同的目标函数，变化不同的强化学习算法来优化投资组合，从而观察哪种方法的组合更有利于实现投资组合的动态优化。其中，深度确定性策略梯度(Deep Determination Policy Gradient,DDPG)是强化学习中的另一种较常用的方法，它结合了深度学习的感知能力与强化学习的决策能力，能够有效解决复杂系统的感知决策问题。

(2)Calmar/Sharpe+A+RRL/DDPG

本研究所提出的模型在每次交易的最后阶段都加入了动态止损机制，但是无法保证这种止损机制在市场环境变化的情况下依然有效。因此有必要将无动态止损机制的交易策略作为基准策略，进行对比，以此来验证该止损机制在投资组合优化过程中能够避免相应投资损失的有效性。

四、实验结果分析

(一)数据收集与处理

我们从中国股票市场收集了21只股票数据作为研究样本。由于我们需要用到沪深300指数(HS300)数据，而HS300是由沪深证券交易所于2005年4月8日联合发布，为了保证我们整个研究数据的一致性，故中国市场所有样本数据的时间范围为2005年4月8日至2019年3月13日。其中，训练集数据的时间范围为2005年4月8日至2015年9月15日，包含2 550个交易日，测试集数据的时间范围为2015年9月16日至2019年3月13日，包含850个交易日。此外，许多研究表明，对于个人投资者而言，持有成百上千个资产作为投资组合是不现实的(Almahdi和Yang，2017[32]；Kocuk和Cornuéjols，2020[39]；Tanaka等，2000[40])。例如，Tanaka等(2000)[40]选取了9种证券作为样本，形成了最优投资组合。Almahdi和Yang(2017)[32]构建了一个包含5种资产的投资组合。本研究分别从中国市场随机选取了21只股票作为研究样本，这足以支撑个人投资者投资组合优化的研究。

所有的样本数据都涉及股票调整后的开盘价、收盘价、最高价、最低价和交易量，均为日度数据。中国股票市场数据来源于沪深300指数(11只股票)和中证500指数(10只股票)。对于缺失数据，若为交易日停牌现象，则取停牌之前最后一个交易日的数据，若为非交易日，则直接删除空白数据。这些股票的收盘价的描述性统计如表1所示。我们可以看出股票000538.sz的日平均价格最高，为45.04元，000012.sz的标准差最低，为2.69元，紧随其后的是000008.sz，为2.88元。

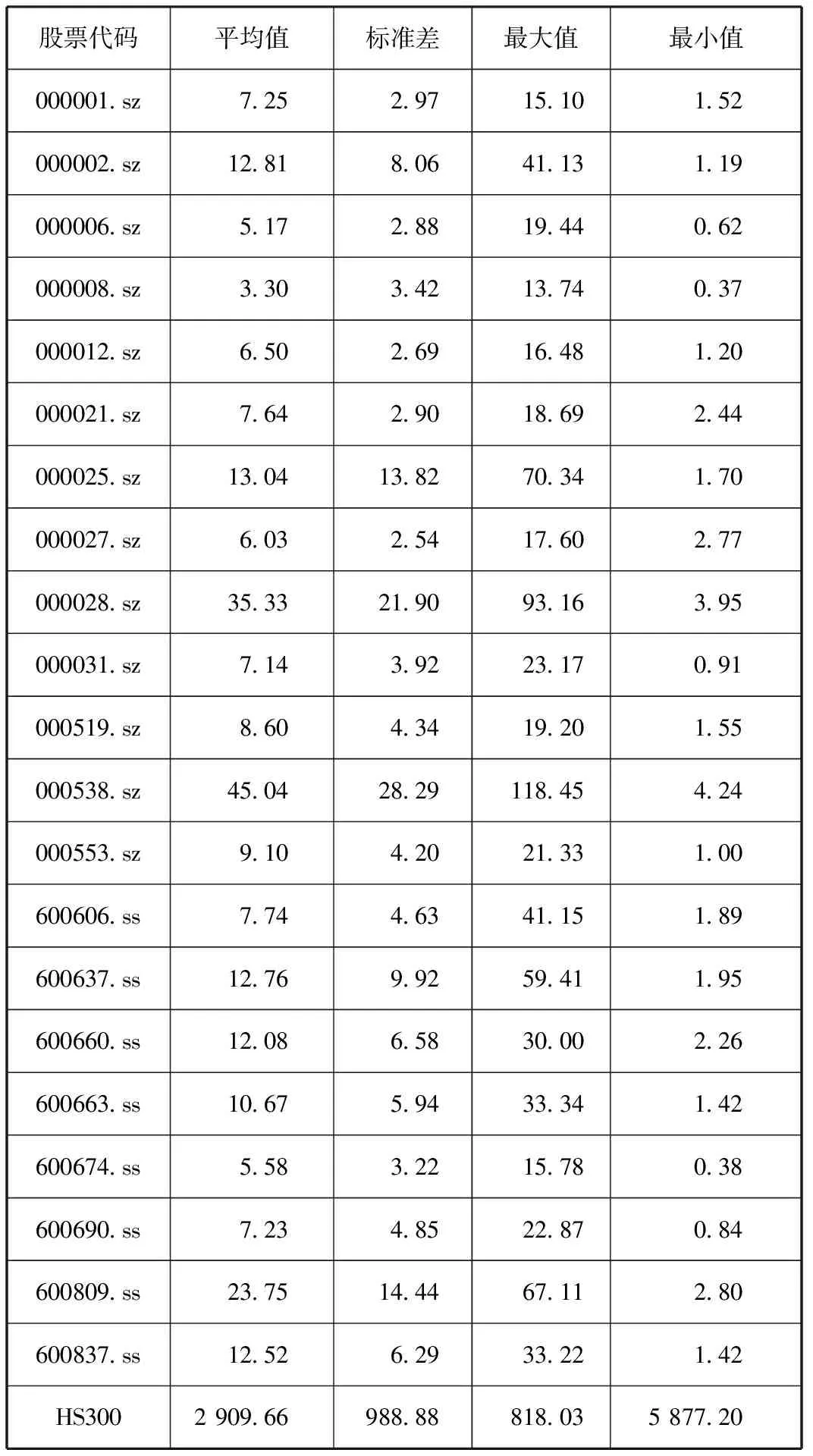
表1样本数据的描述性统计 (单位：元)

在实际金融交易场景中，交易次数不应过于频繁，也不该间隔太久，许多研究表明以两周(约10个交易日)为交易周期对个人投资者而言是比较合理的(Mousavi等，2014[41]；Almahdi和Yang，2019[33])。结合已有文献和实际情况，本研究以两周(10个交易日)为一个交易周期T，并按照交易周期T对样本数据进行划分。最终训练集数据包含了255个交易周期，测试集数据包含了85个交易周期。由于数据选择的范围可能会影响最后实验结果，故我们采用了一种多周期重叠式的投资组合交易训练方式，以便每次训练都能够包含最新的市场数据，提升模型训练的效率。我们设置训练窗口大小为一周(5个交易日)，训练窗口将在每次交易决策后向后逐步移动。本研究的实验结果均是基于以交易周期T划分的数据集来模拟市场交易所获得。

(二)投资组合优化的绩效结果对比

参考相关实证研究(Almahdi和Yang，2017[32]；Paiva等，2019[1])，我们分别对交易成本为0bps、0.05 bps及0.10 bps的情况进行了仿真，并展示了最终的投资组合优化结果，这也符合我国股票市场的交易费用管理规范。本研究中的交易成本只考虑了佣金。表2至表5展示了Sharpe+A+RRL(S-A-R)、Sharpe+A+RRL(Stop-loss)(S-A-R-SL)、Calmar+A+RRL(C-A-R)、Calmar+A+RRL(Stop-loss)(C-A-R-SL)、Sharpe+A+DDPG(S-A-D)、Sharpe+A+DDPG(Stop-loss)(S-A-D-SL)、Calmar+A+DDPG(C-A-D)和Calmar+A+DDPG(Stop-loss)(C-A-D-SL)模型对投资组合进行优化之后的金融绩效结果对比，为了使表更简洁，我们分别采用了各个模型的简称。其中，表2表示无交易成本，表3表示交易成本为0.05bps的情况，表4表示交易成本为0.1bps的情况。面板A、B和C分别描述了以交易周期T为单位，优化后的投资组合的收益特征、风险特征和风险-收益特征。

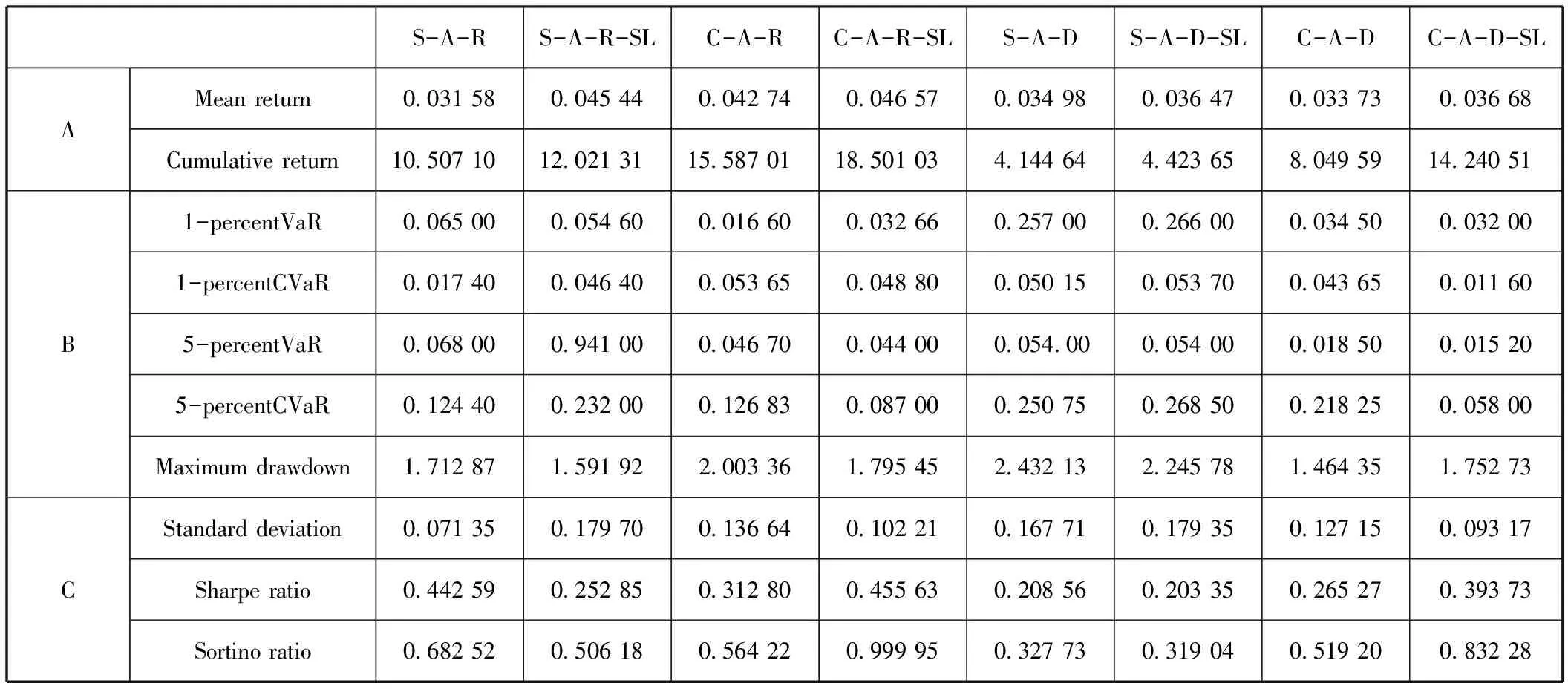
表2无交易成本的投资组合绩效特征

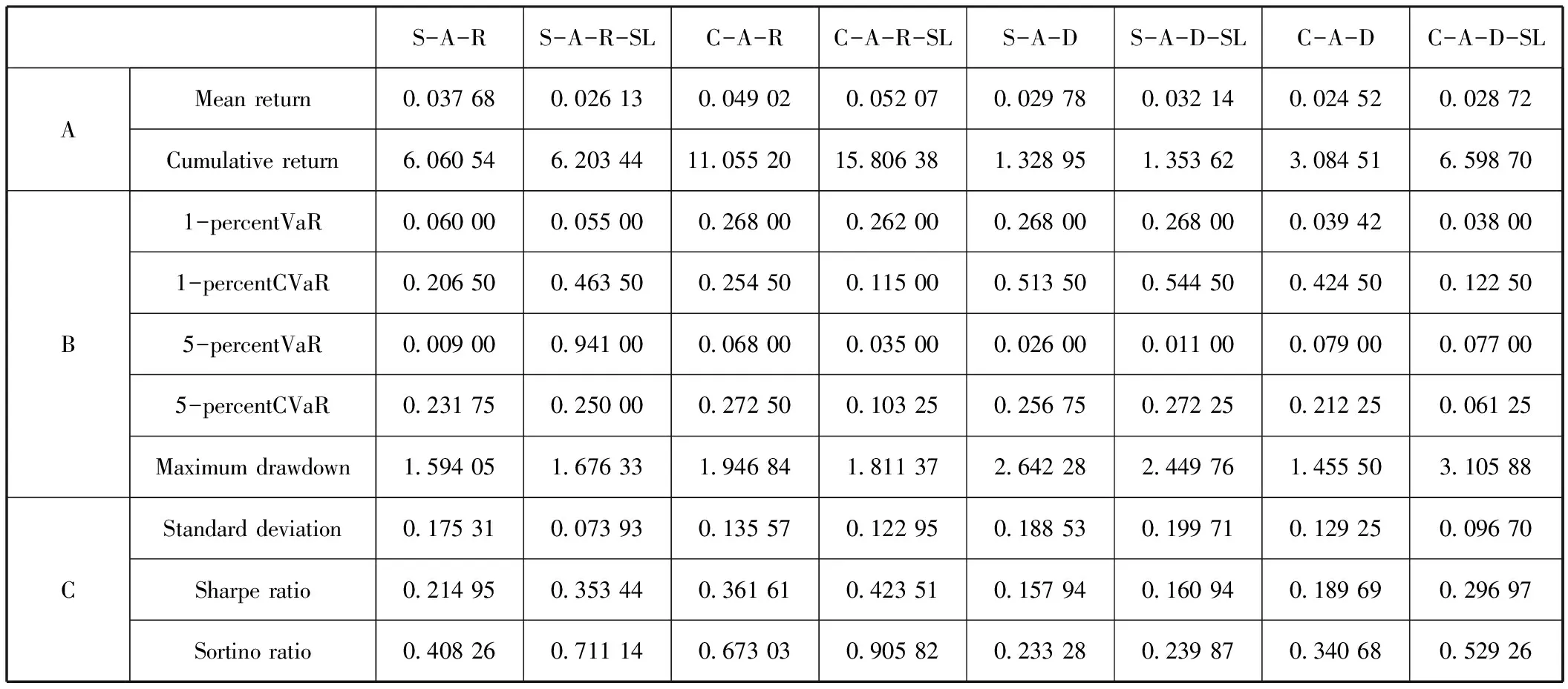
表3含交易成本的投资组合绩效特征(0.05bps)

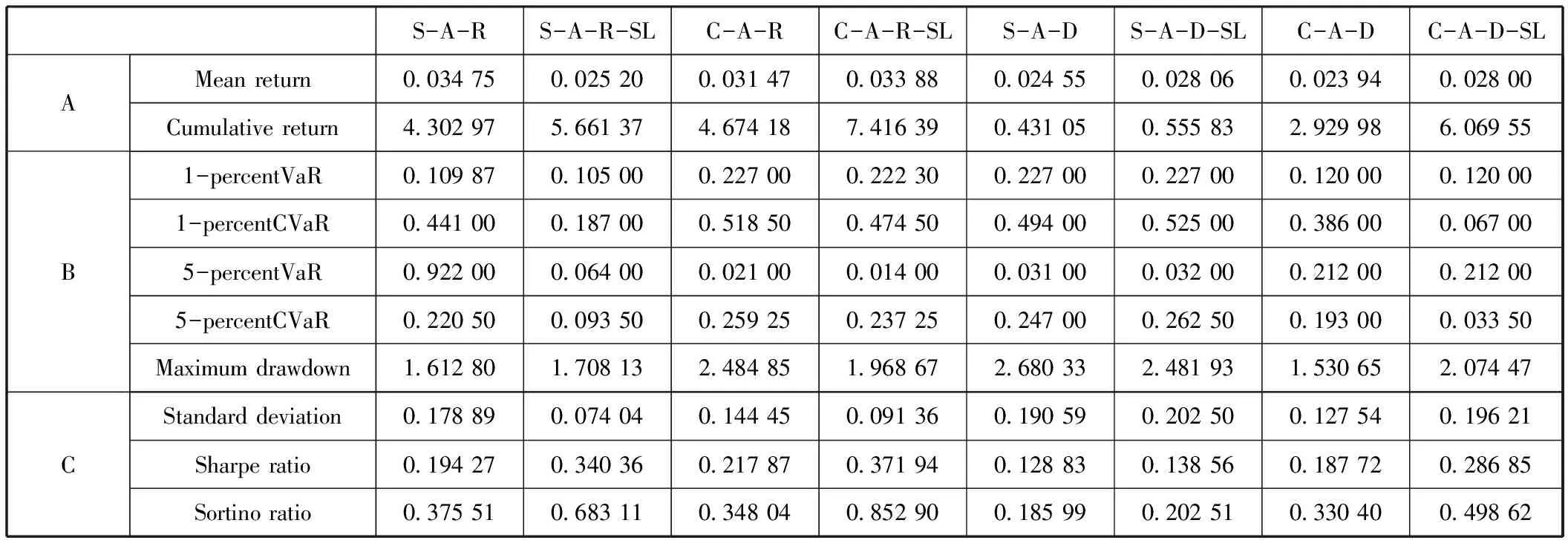
表4含交易成本的投资组合绩效特征(0.1bps)

收益特征：在表2的面板A中，我们可以发现，相比于其他的基准模型，以卡玛为目标函数且带有动态止损机制的Calmar+A+RRL(Stop-loss)模型优化后的投资组合实现了最高平均收益率0.046 57和累计收益率18.501 03。当考虑了交易成本0.05 bps之后，如表3的面板A所示，Calmar+A+RRL(Stop-loss)模型依然保持着最优的平均收益率(0.052 07)和累计收益率(15.806 38)。Calmar+A+RRL模型的平均收益率和累计收益率均位居第二，分别为0.049 02和11.055 20。当考虑了交易成本0.1bps之后，如表4的面板A所示，在累计收益率方面，Calmar+A+RRL(Stop-loss)模型实现了最高值7.416 39，其次是Calmar+A+DDPG(Stop-loss)。在交易周期内的平均收益率方面，Sharpe+A+RRL模型实现了最高值(0.034 75)，然后是Calmar+A+RRL(Stop-loss)模型(0.033 88)。

风险特征：在表2至表4的面板B中，可以观察到与风险特征对应的风险价值(Value at Risk，VAR)、条件风险价值(Conditional Value at Risk，CVaR)及最大回撤率(Maximum drawdown)。当交易成本为0bps时，Calmar+A+DDPG(Stop-loss)模型交易后的投资组合在5%置信水平上VAR和CVAR都实现了最低值，分别为0.015 20和0.058 00。Calmar+A+RRL和Sharpe+A+RRL模型交易后的投资组合分别实现了最低的1% VAR(0.016 60)和1%CVAR(0.017 40)。当交易成本为0.05bps时，Calmar+A+DDPG(Stop-loss)模型交易后的投资组合实现了最低的1% VAR(0.038 00)和5% CVAR(0.061 25)，Sharpe+A+DDPG(Stop-loss)模型在5%置信水平上CVAR实现了最低值0.011 00，此外，Calmar+A+RRL(Stop-loss)模型也实现了比较低的1% CVAR(0.011 50)和5%VAR(0.035 00)。当交易成本增加至0.1bps时，Sharpe+A+RRL(Stop-loss)模型实现了最低的1%VAR(0.105 00)，Calmar+A+RRL(Stop-loss)模型实现了最低的5%VAR(0.014 00)，Calmar+A+DDPG(Stop-loss)模型实现了最低的1%CVAR(0.067 00)和5%CVAR(0.033 50)。最大回撤率指的是某一段时期内投资组合的收益率从最高点开始回落到最低点的幅度，描述的是投资者可能面临的最大损失。在最大回撤率方面，我们发现，Calmar+A+DDPG模型优化后的投资组合在不同的交易成本情况下，均实现了最低的最大回撤率。通过以上分析，我们并没有发现在投资组合风险维度表现最好且稳定的模型。

风险-收益特征：在表2至表4的面板C中，我们讨论了基于各个模型交易之后的投资组合相应的风险-收益情况。具体来讲，在标准差方面，当无交易成本时，Sharpe+A+RRL模型实现了最低值0.071 35，Calmar+A+DDPG(Stop-loss)模型紧随其后，标准差为0.093 17，然后是Calmar+A+RRL(Stop-loss)模型(0.102 21)。当交易成本增加至0.05bps时，Sharpe+A+RRL(Stop-loss)表现最好，标准差仅为0.073 93，Calmar+A+DDPG(Stop-loss)模型紧随其后，标准差为0.096 70。当交易成本为0.1bps时，Sharpe+A+RRL(Stop-loss)模型优化的投资组合实现了最低的标准差值0.074 04，其次是Calmar+A+RRL(Stop-loss)模型(0.091 36)。在夏普比率方面，无论是否考虑交易成本，我们可以发现，Calmar+A+RRL(Stop-loss)模型优化的投资组合均实现了最优的夏普比率，分别为0.455 63(无交易成本)、0.423 51(0.05bps)、0.371 94(0.1bps)。在索提诺比率方面，我们依然可以发现，在不同的交易成本情况下，Calmar+A+RRL(Stop-loss)模型优化的投资组合依然实现了最优值，分别为0.999 95(无交易成本)、0.905 82(0.05bps)和0.852 90(0.1bps)。而Calmar+A+DDPG(Stop-loss)模型在无交易成本时位居第二(0.832 28)，Sharpe+A+RRL(Stop-loss)在0.05交易成本时位居第二(0.711 14)。

根据以上讨论和分析，我们发现，在投资组合的收益特征、风险特征及年度收益-风险特征方面，加入动态止损机制的交易模型Calmar+A+DDPG(Stop-loss)、Calmar+A+RRL(Stop-loss)、Sharpe+A+DDPG(Stop-loss)、Sharpe+A+RRL(Stop-loss)的综合表现要优于未加入该机制的Calmar+A+DDPG、Calmar+A+RRL、Sharpe+A+DDPG、Sharpe+A+RRL模型。此外，以卡玛比率为目标函数的模型Calmar+A+RRL(Stop-loss)、Calmar+A+DDPG(Stop-loss)模型优化后的投资组合的综合表现优于以夏普比率为目标函数的模型Sharpe+A+RRL(Stop-loss)、Sharpe+A+DDPG(Stop-loss)。其中，Calmar+A+RRL(Stop-loss)模型优化后的投资组合的综合表现优于其他基准模型。

(三)投资组合优化结果可视化

为了更加直观地比较各个模型对投资组合的优化效果，我们接着对Calmar+A+DDPG(Stop-loss)，Calmar+A+RRL(Stop-loss)，Sharpe+A+DDPG(Stop-loss)，Sharpe+A+RRL(Stop-loss)这四种综合表现更优的模型在样本测试集期间(2015年9月16日至2019年3月13日)优化后的投资组合的累计收益率进行了可视化展示。首先，我们对不同的目标函数的优化模型对应的投资组合的累计收益率(0bps)进行了纵向对比。从图3可以看出，加入了动态止损机制的投资组合优化方法确实比不加入该机制的方法实现了更高的累计收益率，而且无论是否加入动态止损机制，无论如何设置目标函数，各个模型优化的投资组合所实现的累计收益率始终高于沪深300指数HS300的累计收益率，也就是中国股票市场的基本水平(黄东宾等，2017[42]；曾志平等，2017[28])。图4展现了无交易成本时每个模型对应的累计收益率。显然，在四个模型之中，Calmar+A+RRL(Stop-loss)模型具有更高的累计收益率，最终的累计收益率约达到了18.501 03。位居第二的是Sharpe+A+DDPG(Stop-loss)模型，累计收益率为15.587 01。然后是Calmar+A+DDPG(Stop-loss)模型(15.587 01)和Sharpe+A+RRL(Stop-loss)模型(10.507 10)。此外，我们还需要进一步观察不同模型在不同交易成本水平下的投资组合优化结果。

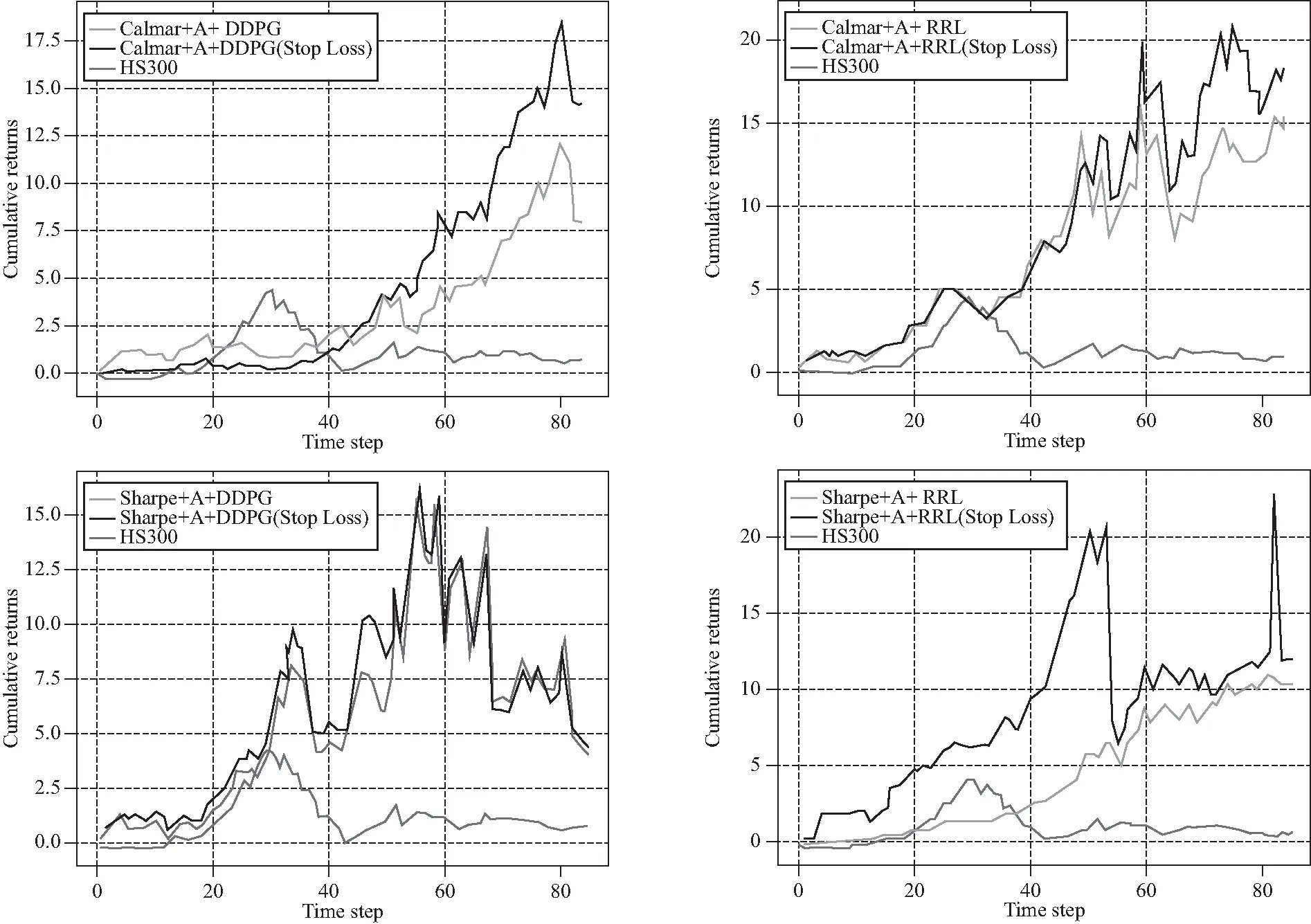
图3 无交易成本时不同目标函数对应的累计收益对比

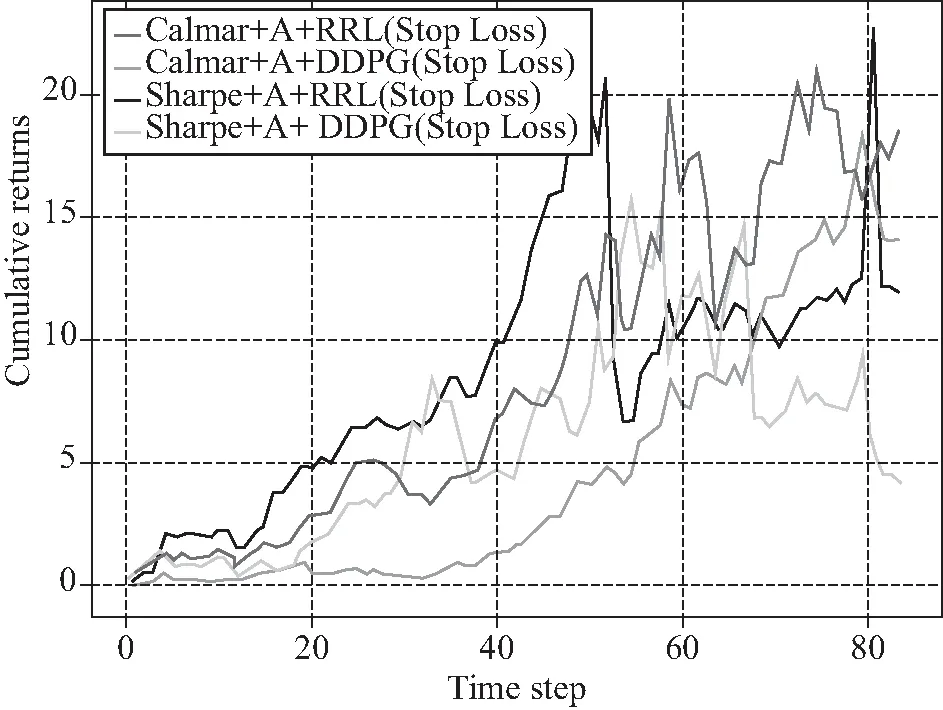
图4 无交易成本时的累计收益

我们接着分别描绘了交易成本为0.05bps和0.10 bps的各个交易策略所对应的投资组合的交易后的累计收益率，结果如图5和图6所示。显然，与无交易成本相比，各个模型交易后的投资组合的累计收益率都有下降的趋势。当交易成本为0.05 bps时，Calmar+A+RRL(Stop-loss)模型依然实现了最大的投资组合最终累计收益率(15.806 38)；Calmar+A+DDPG(Stop-loss)模型对应的投资组合累计收益率位居第二(6.598 70)，然后是Sharpe+A+RRL(Stop-loss)模型(6.203 44)。当交易成本为0.1 bps时，Calmar+A+RRL(Stop-loss)模型交易后的投资组合的最终累计收益率(7.416 39)依然大于其他模型，Calmar+A+DDPG(Stop-loss)模型对应的投资组合累计收益率位居第二(6.069 55)。接着是Sharpe+A+RRL(Stop-loss)模型(5.661 37)。

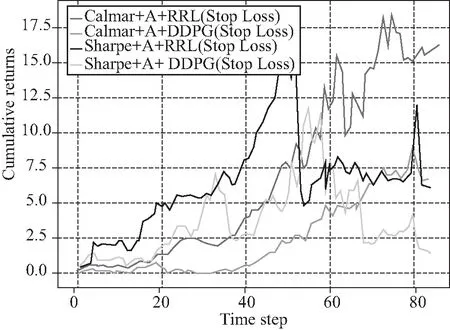
图5 含交易成本时的累计收益(0.05bps)

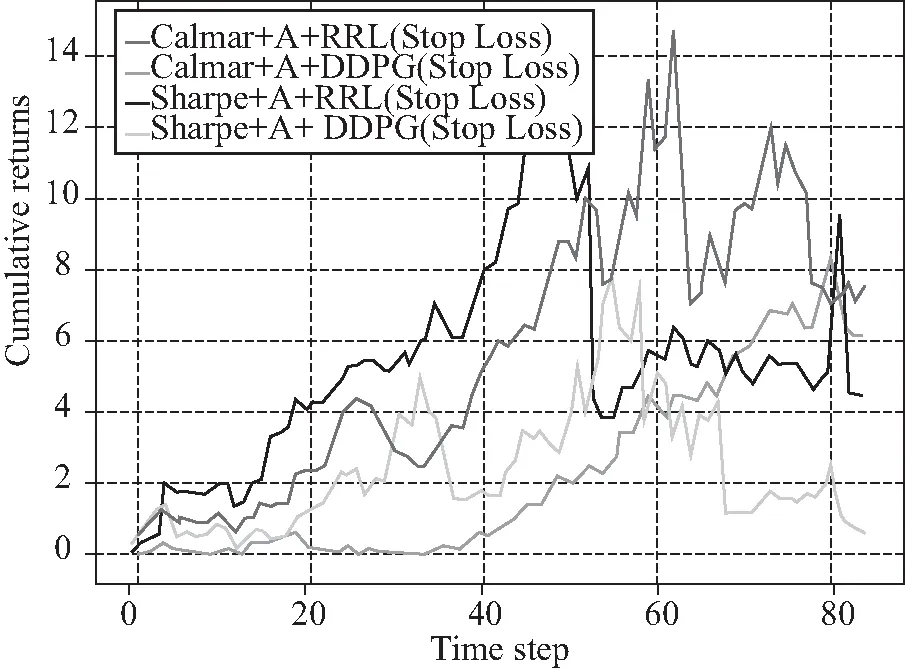
图6 含交易成本时的累计收益(0.1bps)

通过将不同的模型优化后的投资组合的累计收益率进行可视化对比，容易发现，无论是否考虑交易成本，以卡玛比率为目标函数且加入了动态止损机制的投资组合优化模型Calmar+A+RRL(Stop-loss)均实现了较优的结果，实现了投资组合交易的收益最大化。

需要说明的是，本研究参考了Almahdi和Yang(2017)[32]的研究，该研究所采用的投资组合优化模型可以简写Calmar+RRL(Stop-loss)，我们在该模型的基础之上进行了改进和拓展。与已有研究[32]相比，本研究中的投资组合优化模型Calmar+A+RRL(Stop-loss)将体制转换模型与循环强化学习方法相结合，可以在不同的市场环境状态下选择不同的神经网络权重来应对市场风格的变化，此外本研究还设计了投资组合内部资产与外部资产池进行动态交易场景来实时更替投资组合的资产构成和投资配置比例。由此我们将本研究中综合表现最好的模型Calmar+A+RRL(Stop-loss)与Almahdi和Yang(2017)[32]提出的投资组合优化模型Calmar+RRL(Stop-loss)进行了累计收益率的可视化比较。如图7所示，Calmar+A+RRL(Stop-loss)模型优化后的投资组合所实现的最终累计收益率(18.501 03)高于Calmar+RRL(Stop-loss)模型对应的投资组合最终累计收益率(10.442 89)。

由此我们想要验证不同模型在对投资组合优化过程中产生的交易信号频率如何，因为交易信号的产生频率关系着投资组合优化之后的金融绩效。投资组合包含了9只资产，在动态交易情境下，该投资组合中始终有9个位置留给在相应周期T内符合目标函数最大化的资产。于是，我们随机选取了三个位置，它们的交易信号如图8、图9和图10所示。从横向对比来看，在相同的目标函数条件下，加入动态止损机制的模型比没有动态止损机制的模型的交易信号产生的频率稍微高一点。而从纵向对比来看，以卡玛比率为目标函数的投资组合优化模型Calmar+A+RRL(Stop-loss)、Calmar+A+DDPG(Stop-loss)、Calmar+A+RRL和Calmar+A+DDPG产生的交易信号比以夏普比率为目标函数的投资组合优化模型Sharpe+A+RRL(Stop-loss)、Sharpe+A+DDPG(Stop-loss)、Sharpe+A+RRL和Sharpe+A+DDPG产生的相应交易信号频率更低、一致性更高。这也能够说明我们在同一位置上持有资产的时间更长，从而在一定程度上降低了交易成本对收益的影响。这也进一步解释并验证了Calmar+A+RRL(Stop-loss)模型在动态交易情境下比其他模型表现更好。

图8 交易信号(位置一)

图9 交易信号(位置二)

图10 交易信号(位置三)

(四)稳健性检验

基于前面的投资组合优化结果对比和可视化分析，可以看出，在不同的交易成本情况下，Calmar+A+RRL(Stop-loss)模型的优化效果都较为全面地、显著地优于其他基准模型，即Calmar+A+RRL(Stop-loss)模型的鲁棒性得到了验证。为了对实验结果进行更加严谨的分析和检验，我们进一步对Calmar+A+RRL(Stop-loss)、Calmar+A+DDPG(Stop-loss)、Calmar+A+DDPG、Sharpe+A+RRL(Stop-loss)和Sharpe+A+DDPG(Stop-loss)模型在周期收益率数据集上的差异性进行了显著性检验。首先，我们对所有模型构建的投资组合的每个交易周期的收益率数据集进行了正态性检验。如表5所示，P值均为0.00，故拒绝这些数据集服从正态分布的原假设。因此，我们选择了非参数检验。表6为Kruskal-Wallis检验的结果，易得不同模型平均周期收益率分布的无差异的非参数假设被拒绝。由于Kruskal-Wallis检验不显示两两模型之间的差异关系，于是我们采用了Mann-Whitney检验，表7、表8和表9分别展示了无交易成本、交易成本为0.05bps和0.1bps时各个模型对应的交易周期收益率差异的显著性检验结果。从这些检验结果中可以看出，在95%甚至99%的置信水平上，Calmar+A+RRL(Stop-loss)模型优化后的投资组合与Calmar+A+DDPG(Stop-loss)、Calmar+A+DDPG、Sharpe+A+RRL(Stop-loss)和Sharpe+A+DDPG(Stop-loss)模型优化后的投资组合在收益率上差异性显著。

表5投资组合周期收益率的正态性检验(P-value)

表6 投资组合周期收益率的Kruskal-Wallis检验(P-value)

表7无交易成本的投资组合周期收益率的Mann-Whitney检验(P-value)

表8含交易成本(0.05bps)的投资组合周期收益率的Mann-Whitney检验(P-value)

表9含交易成本(0.1bps)的投资组合周期收益率的Mann-Whitney检验(P-value)

五、研究结论

本研究基于循环强化学习RRL提出了一种智能投资组合动态优化方法Calmar+A+RRL(Stop-loss)，该方法能够依据不同风险约束的目标函数来应对不同的市场风格变化，并根据当前市场的金融时间序列信息，通过投资组合内部资产与外部资产池动态交易的形式，来实时调整投资组合资产构成及资产配置。具体而言，在每一个交易周期T，该方法都会依据包含风险约束的目标函数和市场的实时变化来从外部市场资产池中为投资组合动态挑选符合目标函数的资产，然后基于RRL方法对投资组合的资产权重进行配置并为每个资产生成相应的交易信号，从而基于这种动态交易的方式来优化投资组合。此外，我们在动态交易之后加入了一个动态止损机制，当止损机制被触发，交易将被停止，然后重新开始新一轮周期的投资组合优化。本研究基于中国股票市场数据进行了实证分析，得出了以下几个主要结论。

第一，我们发现在交易成本和市场状况都发生变化的情况下，加入动态止损机制的投资组合优化模型Calmar+A+DDPG(Stop-loss)、Calmar+A+RRL(Stop-loss)、Sharpe+A+DDPG(Stop-loss)和Sharpe+A+RRL(Stop-loss)在收益、风险和风险-收益三个维度的综合表现要优于未加入该机制的Calmar+A+DDPG、Calmar+A+RRL、Sharpe+A+DDPG和Sharpe+A+RRL模型。这说明在投资组合优化过程中，由于市场环境的不断变化，任何一种优化方法或者模型都不能永久获益，因此有必要加入与市场环境和资产信息变化相适应的动态止损机制，而本研究提出的动态止损机制可以从一定程度上控制投资组合优化过程中的风险。

第二，研究发现，以卡玛比率为目标函数的模型Calmar+A+RRL(Stop-loss)、Calmar+A+DDPG(Stop-loss)模型优化后的投资组合的综合表现优于以夏普比率为目标函数的模型Sharpe+A+RRL(Stop-loss)、Sharpe+A+DDPG(Stop-loss)。因此，在投资组合的优化中考虑下行风险约束比考虑总体风险更有利于实现既定投资风险下的收益最大化。

第三，无论是否考虑交易成本，综合来看，以卡玛比率为目标函数且带有动态止损机制模型Calmar+A+RRL(Stop-loss)所优化的投资组合的各项金融指标性能都显著优于其他基准模型所对应的投资组合。这说明该模型可以适应不同的市场情况，有效过滤市场噪声并识别重要的交易信号，进而帮助投资者获取更高的收益。而且Calmar+A+RRL(Stop-loss)模型在投资组合动态优化方面的有效性在新兴的中国股票市场得到了充分的检验。

第四，通过对比本研究提出的模型Calmar+A+RRL(Stop-loss)和Almahdi和Yang的研究(2017)[32]所采用的模型Calmar+RRL(Stop-loss)，在相同的数据集和模型参数设定条件下，研究发现Calmar+A+RRL(Stop-loss)模型实现了比Calmar+RRL(Stop-loss)更高的投资组合最终累计收益率。这说明了依据市场环境变化和动态交易方式来选择投资组合的资产构成并考虑风险约束因素的必要性。