基于电子分层模型和凝聚策略的密度峰值聚类

杜淑颖,施天豪,丁世飞

(1.中国矿业大学 计算机科学与技术学院,江苏 徐州 221116;2.徐州生物工程职业技术学院 信息管理学院,江苏 徐州 221000)

进入信息时代,信息科学技术广泛地渗透到社会生活中的各个领域并产生了各种各样的数据。如何从多样的数据中获取有用的信息是数据挖掘研究的焦点问题。聚类分析是数据挖掘领域的一项重要内容,它能在标签未知的情况下通过数据间的相似度进行分类,使同类的数据之间具有较高的相似度。聚类分析发掘数据的潜在联系,得到关键信息从而支持决策。因此,它在模式识别、图像分割、社区发现等诸多领域应用广泛[1,2]。

密度峰值聚类[3](Density peaks clustering,DPC)是由Rodriguez等于2014年提出的一种基于密度的简单高效的聚类算法。算法通过密度ρ和相对距离δ两个基本属性完成聚类。DPC是密度聚类的一种代表算法,其无需迭代,可以对非球形的数据聚类并得到较为满意的结果。密度峰值聚类的优点较为突出,但是它的缺点仍然不容忽视:(1)人工选取聚类中心会导致较大的聚类误差;(2)在密度不均匀的流形数据集上得不到正确的聚类结果。高密度的数据点通常被选取为聚类中心点,因此在密度不均匀的数据集中低密度簇的中心点往往会被忽略,由于中心点的错误选取而导致的“多米诺效应”往往会造成错误的聚类结果。密度峰值聚类需要进一步研究和改进。

为了改善上述不足,近些年来很多密度峰值改进算法被提出[4-13]。针对第一个弊端的研究较少,Xu等[4]基于轮廓系数提出一种新指标DCI能自动得到聚类数目无需人工干预。Yan等[5]提出ADPC算法,其利用一种异常值统计检测方法在决策图中自动找出聚类中心。而针对第二个弊端,学者们开展了广泛的研究并提出较多的改进算法。Xie等[6]提出FKNN-DPC算法,其利用K近邻概念计算密度,并通过K近邻和模糊加权K近邻来改善分配过程,FKNN-DPC在流形数据集上具有比DPC更好的聚类结果。Liu等[7]提出了SNN-DPC算法,其利用了共享近邻SNN重新定义了局部密度ρ和相对距离δ。SNN-DPC引入了两步分配策略:必然从属和可能从属,使得聚类的精度大大提高。Du等[8]提出DP-DA算法,通过密度自适应度量重新定义了数据点之间的相似度,相对于用欧氏距离作为相似度度量的DPC算法具有更好的聚类性能。Seyedi等[9]提出DPC-DLP算法,利用图标签传播对剩余点分配并形成最终簇类。这些算法一般都是通过K近邻计算数据点局部密度,默认这些近邻点在密度计算过程中所起的作用是一致的,而这导致不同密度簇之间的密度差过大,低密度簇容易被忽略造成较大的聚类误差。基于以上分析,本文提出一种基于电子分层模型和凝聚策略的密度峰值聚类(Density peaks clustering based on electronic shells model and merging strategy,EMDPC)。其仿照电子分层模型给不同的近邻点分层,并在不同层次分配不同的权重,缩小了不同簇类之间的密度差,可以在具有不同密度簇的流形数据上更为轻易地识别出低密度簇,进一步提高聚类精度。另外,EMDPC通过凝聚策略能很好适用于密度不均匀的流形数据,较好地解决了DPC存在的问题。

1 DPC算法原理

DPC是近来提出的一种高效的聚类算法,它能将任意形状的数据聚类且无需考虑数据空间的维度。DPC没有迭代,不需要预设聚类数目,仅需要较少的参数,因此它具有非常广阔的应用前景。算法的核心思想基于两个基本假设:(1)聚类中心点处于稠密区域,且其密度比周围数据点的密度更大;(2)聚类中心点与比其密度大的数据点之间的距离更大。因此,DPC通过数据点的两个基本属性:密度ρ和相对距离δ来完成整个聚类过程。

假设有数据集X={x1,x2,…,xn},基于第一个假设,DPC定义每个数据点的局部密度,如式(1)所示

(1)

χ(x)的定义如式(2)

(2)

式中:dist(i,j)表示点xi和xj之间的欧式距离;dc是一个输入参数,代表截断距离。这种方法得到xi的密度等于与点xi间的距离小于dc的所有数据点个数。而当数据集规模较小时,DPC也可以通过一种高斯核函数来计算数据点局部密度,如式(3)所示

基于第二个假设,相对距离δi被定义为点xi与比它密度大的数据点之间的最小距离

(4)

而对于密度最大的数据点,其相对距离为

(5)

在得到数据点的密度ρ和相对距离δ之后,以ρ为横轴,δ为纵轴画出决策图,通过选择具有较大ρ和δ值的点作为聚类中心,将数据标签分配到剩余的非中心点上,得到最终的聚类结果。如图1所示,图1(a)为28个二维数据点的分布图,图1(b)为对应画出的决策图,不同的颜色表示不同的簇类,从决策图中可以看出在右上区域的两个点具有较大的ρ和δ值,因此这两个点被选取为聚类中心,其余非中心点被分配到这两个中心所形成的簇类中。

值得注意的是,DPC的关键步骤是通过决策图选取聚类中心。这一步中通过人工干预选择聚类中心点具有较大的误差,聚类中心和非中心点之间的界限有时非常模糊,通过人工干预难以辨别。图2是DPC在Jain数据集上的决策图,图中有颜色的两个点为真实聚类中心,在中心点数目未知的情况下依靠人工精准选择十分困难。因此,提出一种改进算法以解决这些不足势在必行。

图2 DPC在Jain数据集上的决策图

2 EMDPC算法

2.1 基于电子分层模型的局部密度计算

EMDPC算法的提出是为了解决密度峰值在密度不均匀的流形数据上聚类性能不佳,需要人工干预选择聚类中心进而加大聚类误差的问题。它基于这样一个假设:有一组数据规模为n的数据X={x1,x2,…,xn},对于其中的任意一个点xi,本文认为xi的近邻点对于xi密度计算的贡献是不同的,这种不同不仅仅局限于它们之间的距离。因此本文将xi的近邻点分成几个不同的层次,给每个层次分配不同的权重,代表这个层次上的点对于xi密度的贡献程度。另外,如果将剩余点按照与xi的相似度大小排序,会发现与xi较相似的点比较少,与xi不太相似的点更多,这符合电子分层模型中内层电子少,外层电子数多的情况,如图3(a)所示。因此,利用电子分层模型来改进密度计算,缩小不同簇间密度差,进一步提高聚类精度。

数据点分层模型如图3(b)所示,每个数据点的层级轨道可以表示为l(1≤l≤L),其中L表示总轨道数,在第l层轨道内存在l+1个数据点,则点xi的密度定义为

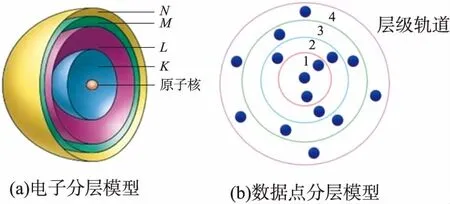
图3 分层模型

(6)

式中:dij表示点xi与点xj之间的距离;dsum表示所有层级轨道内的数据点与xi的距离之和;ω是每个层级轨道所分配到的权重,其计算为

ωl=exp(-l)

(7)

可以看到层级l越大,权重ωl就越小,即如果一个数据点距离xi越远,所在的轨道数越大,它在xi密度计算过程中所起到的作用越小。

图4为稠密区域内数据点和稀疏区域内数据点的层级差异,对每个层级轨道分配不同的权重,等效于缩小在外层轨道内的点到核心点的距离。通过这种方式将低密度区域内数据点的密度适当增大,能缩小不同簇类之间的密度差,有效发现低密度簇。

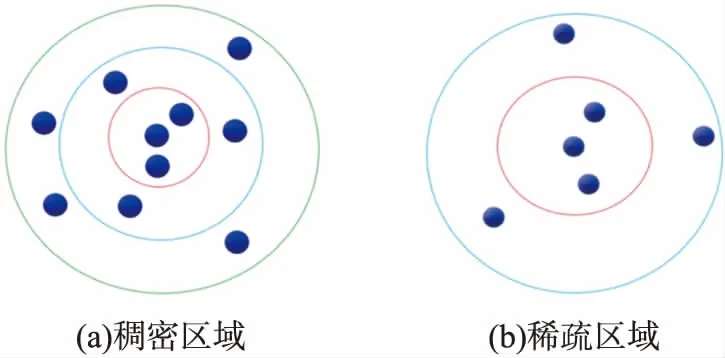
图4 稠密区域和稀疏区域的层级差异

2.2 子簇凝聚策略

在得到ρ和δ之后,画出决策图,得到尽可能多的子簇。然而如何合并子簇,使最终的聚类结果更精确是本文研究的主要问题之一。对于两个高相似度子簇,要使得合并之后的结果尽可能与真实划分保持一致。为此,两个需要合并的子簇应该具有以下特点:(1)较多的共同近邻;(2)平均密度应该尽可能相近;(3)簇中心应尽可能接近;(4)子簇间的最短距离应尽可能小。

通过以上分析,首先得到下述定义:

定义1公共近邻[14]。对于任意两个点xi和xj,D(i)表示以xi为核心的L层轨道内的所有数据点集合,则xi和xj在L层轨道内的共同近邻如式(8)所示

SNN(xi,xj)=D(i)∩D(j)

(8)

定义2簇间平均密度差。簇间平均密度差为两个簇类平均密度的差的绝对值,其计算公式见式(9)

den_diff(ci,cj)=|ρavg(ci)-ρavg(cj)|

(9)

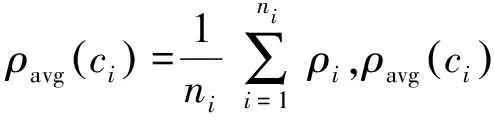
定义3簇间最短距离[15]。为了减小异常值的影响,最短距离dmin(ci,cj)选取两个簇内nij个点的最短距离的平均值,见式(10)

(10)

式中:nij=ceil(min(ni·10%,nj·10%)),ceil为取整函数。

定义4簇间相似度。假设有两个簇ci和cj,簇ci内共有ni个点,则ci和cj之间的簇间相似度SIM(ci,cj)的定义如式(11)所示

(11)

式中:dij是ci和cj的簇中心点之间的距离。通过上述定义得到的簇间相似度,可以看出两个簇之间的共同近邻越多,簇间距离越短,簇间平均密度差越接近,则两个簇之间的相似度就越高,这符合本文认知中的相似度定义。在得到簇间相似度之后,可以将每两个簇之间的簇间相似度按从大到小排序,把具有最大簇间相似度的两个簇类聚合在一起,直至满足结束条件之后停止子簇凝聚,得到最终的聚类结果。

定义5凝聚结束条件。具有最大相似度的两个子簇在凝聚过程中如果满足以下两种情况中的任意一种,就认为凝聚过程结束,如式(12)所示

(12)

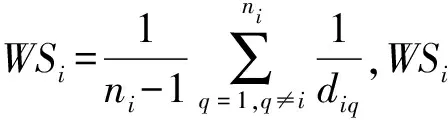
聚类的目标是最大化簇内相似度,如果子簇凝聚后簇内相似度不升反降,则说明不应将子簇凝聚。因此,如果满足以上两个终止条件,则凝聚过程结束。

2.3 算法描述

算法描述见算法1。

算法1EMDPC算法

输入:数据集X={x1,x2,…,xn},分层数L;

输出:聚类结果Y;

1:计算任意两点之间的距离得到距离矩阵D;

2:通过式(6)计算数据点局部密度ρ;

3:通过式(4)和式(5)计算数据点相对距离δ;

4:画出决策图,选择尽可能多的具有相对较大ρ和δ值的点作为聚类中心;

5:将剩余非中心点分配到与其最近的高密度点所在的簇类中,形成子簇;

6:While不满足凝聚结束条件:

7: 通过式(11)计算任意两个子簇之间的相似度;

8: 将相似度最高的两个子簇凝聚,子簇个数减1;

9:End

国有企业要完善内部组织架构，严格按照生产需要和发展目标明确分工，提升工作效率。同时，利用科学手段，完善内部控制管理体系，组建风险评估组和监督部门，对企业进行全面的风险评估和监督工作，实现对企业内部的有效监管，如财务管理、资金流动及财务审计等方面，进而提升国有企业内部沟通的效率[5]。通过高效沟通，不仅增强了国有企业应对风险的能力，同时也实现了企业内部控制的有效实施。

10:输出结束条件终止后的最终结果Y。

2.4 算法复杂度分析

EMDPC的前半部分的复杂度与DPC基本一致:(1)计算距离矩阵需要O(n2);(2)通过电子分层模型计算局部密度,需要O(n2);(3)计算相对距离,所需时间O(n2);(4)排序并分配标签,复杂度为O(nlogn+n),之后将子簇合并,合并过程中:(5)寻找子簇内数据点的共享近邻,时间复杂度为O(n2);(6)计算簇间密度差和簇间最短距离需要O(n2);(7)计算簇间相似度,所需时间O(n2);(8)合并子簇需要O(n)。因此,EMDPC算法总的时间复杂度为O(3n2+nlogn+n+λ(3n2+n))=(1+λ)(3n2+n)+nlogn,其中λ为选取簇类数与真实簇类数之差,即迭代次数。因为有λ≪n,故其时间复杂度可以近似为O(n2)。

3 实验与分析

3.1 实验设置

为了验证EMDPC的可行性和有效性,本文在8个合成数据集和8个真实数据集上进行对比实验,数据集详细信息如表1和表2所示。EMDPC与近几年提出的4种DPC的改进算法:DPC-KNN、SNN-DPC、DPC-SFSKNN以及DPCSA进行对比实验。这4种算法利用不同的改进策略来提升DPC在不同数据集上的聚类精度,具有较好的实验结果,与EMDPC进行对比更能体现出EMDPC的聚类优越性。其中,DPC-KNN和SNN-DPC分别利用K近邻和共享近邻来重新定义数据点局部密度,提升原有DPC的聚类精度,聚类结果得到明显改善;DPC-SFSKNN利用加权K近邻计算数据局部密度,并使用相似度优先算法来分配数据点标签,实验证明其具有不错的聚类结果;DPCSA用一种近邻分配策略来提高DPC在密度分布不均的流形数据集上的聚类精度。这4种算法是较为典型的DPC改进算法,其详细信息见参考文献[7,10,16,17]。

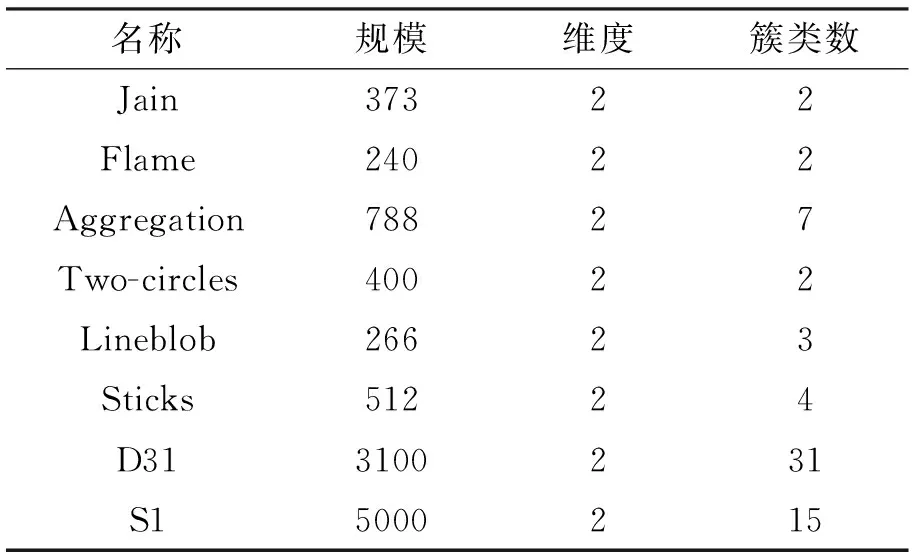
表1 合成数据集详细信息

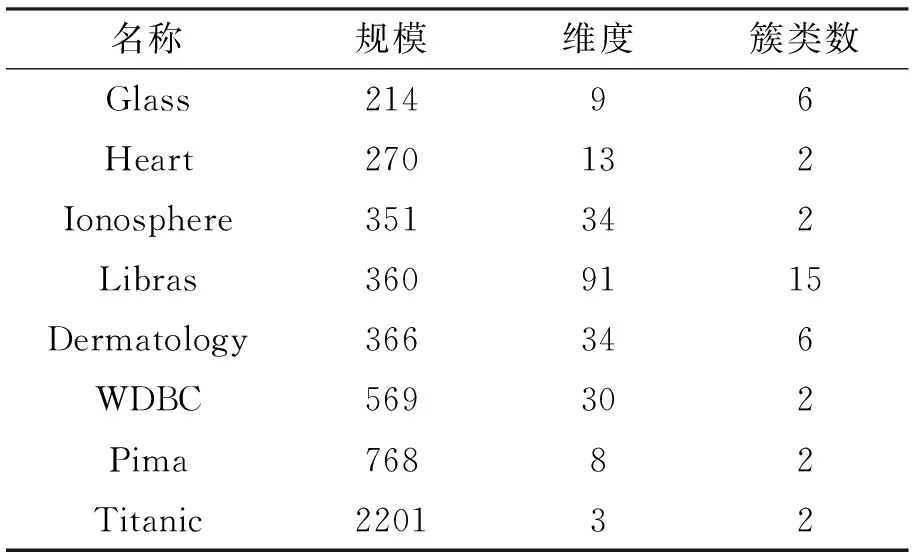
表2 真实数据集详细信息

本文使用聚类精确度(Accuracy,ACC)、调整兰德系数(Adjusted rand index,ARI)和调整互信息(Adjusted mutual information,AMI)3个常用的评价聚类性能的指标来验证聚类结果的优劣,它们取值越接近1表明聚类结果越好。

仿真实验在笔记本电脑上进行,主要配置为Intel Core i7处理器、8 GB内存、Windows10操作系统,集成开发环境为MATLAB 2019b。

3.2 实验结果分析

3.2.1 合成数据集实验分析

本节对8个合成数据集(http://cs.uef.fi/sipu/datasets/)进行分析,它们的具体信息见表1。这些数据集具有不同的规模,不同的流形结构,不同的簇类数目,因此DPC很难在这些数据集上正确聚类。将EMDPC同DPC在二维图形上进行对比,通过图形观察聚类结果,更为直观地了解EMDPC的优越性,其中DPC的参数设置为dc∈{1%,2%,4%,6%}。EMDPC和DPC在8个合成数据集上的聚类结果分别如图5～12所示。图中(a)为EMDPC的聚类结果,(b)和(c)为DPC在参数dc分别取2%和4%的聚类结果。

图5和图6分别是在Jain和Flame上的聚类结果:从(b)和(c)可以看出,DPC都没能将这两个数据准确聚类,其密度分布不均的流形结构让DPC产生了误差;而EMDPC通过层级轨道划分能得到正确的划分结果,其聚类精度均为1,如图5(a)和图6(a)所示。Aggregation数据集如图7所示:在dc=2时,其结果有所偏差;EMDPC得益于密度计算方式和凝聚策略,能自适应识别7个中心点并得到正确的聚类结果。从图8可以看出,Two-circles内圈的密度要比外圈的密度大。DPC无法将Two-circles正确聚类,所得到的两个中心都必定分布在密度较高的内圈中。EMDPC通过分层模型能准确得到内圈和外圈的中心点,而不会将密度较低的外圈分配到高密度的内圈中,再通过凝聚策略得到正确的聚类结果,其精度在DPC基础上提升了100%左右。

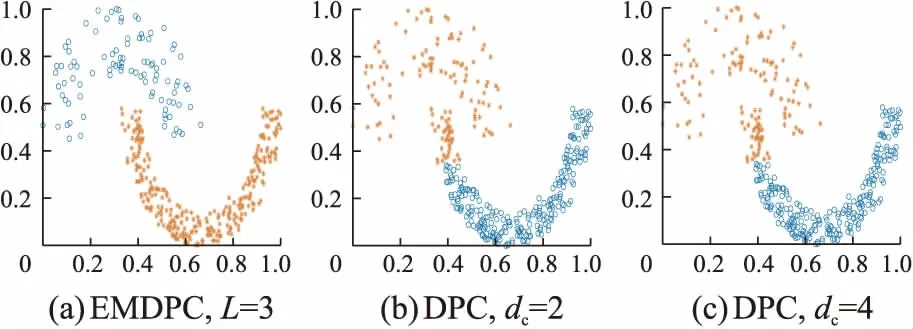
图5 Jain上的聚类结果

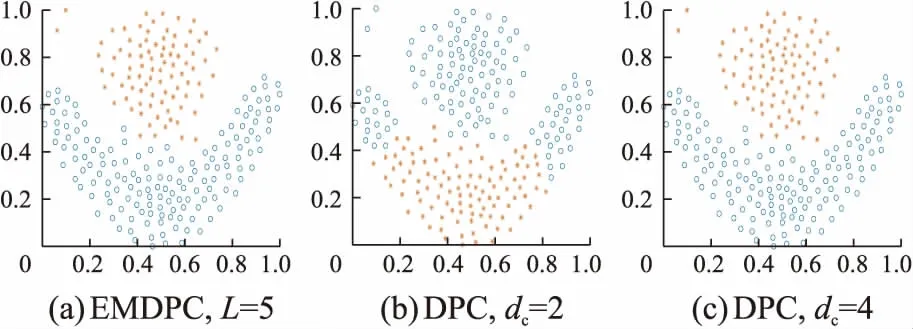
图6 Flame上的聚类结果

DPC在Lineblob和Sticks上均不能准确聚类,原因是这两个数据集密度分布不均匀,DPC识别不出低密度簇。EMDPC通过电子分层模型准确地识别出了这两个数据集中的低密度簇,并通过子簇凝聚策略得到了正确的聚类结果,分别如图9(a)和图10(a)所示。

图10 Sticks上的聚类结果

D31数据集和S1数据集是两个规模较大的合成数据集,这两个数据集中的不同簇类间部分数据点的距离相对较近,簇类间区分的界限比较模糊,因此不容易准确识别数据集中所有簇类。如图11和图12所示,EMDPC由子簇凝聚策略准确识别出了簇类数目,其聚类结果与DPC十分接近。在表3中可以看到EMDPC在D31数据集上的聚类精度为0.971,略大于DPC精度0.967,在S1上,EMDPC取得与DPC一致的聚类结果,充分表明了EMDPC通过分层模型和凝聚策略进行聚类的优越性。

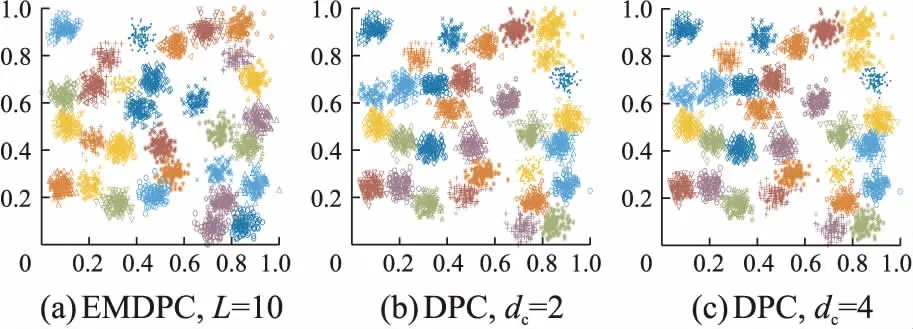
图11 D31上的聚类结果

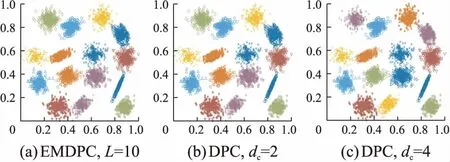
图12 S1上的聚类结果

表3为在8个合成数据集上EMDPC以及其他5种对比算法的详细聚类结果。Par表示相关参数(Parameter,Par),这些算法参数值为取得最佳聚类结果时的值。加粗的数据表示最佳结果。从表中可以看出EMDPC取得了8个数据集上最佳的聚类结果。其中,在Jain、Flame、Two-circles、Lineblob和Sticks数据集上EMDPC均能完美聚类,其聚类精度均为1。在D31和S1数据集上,虽然EMDPC的聚类精度不为1,但其精度在5个对比算法中都是最高的,这充分说明了EMDPC算法比其他聚类算法在密度分布不均的数据集上具有更为优越的聚类性能。

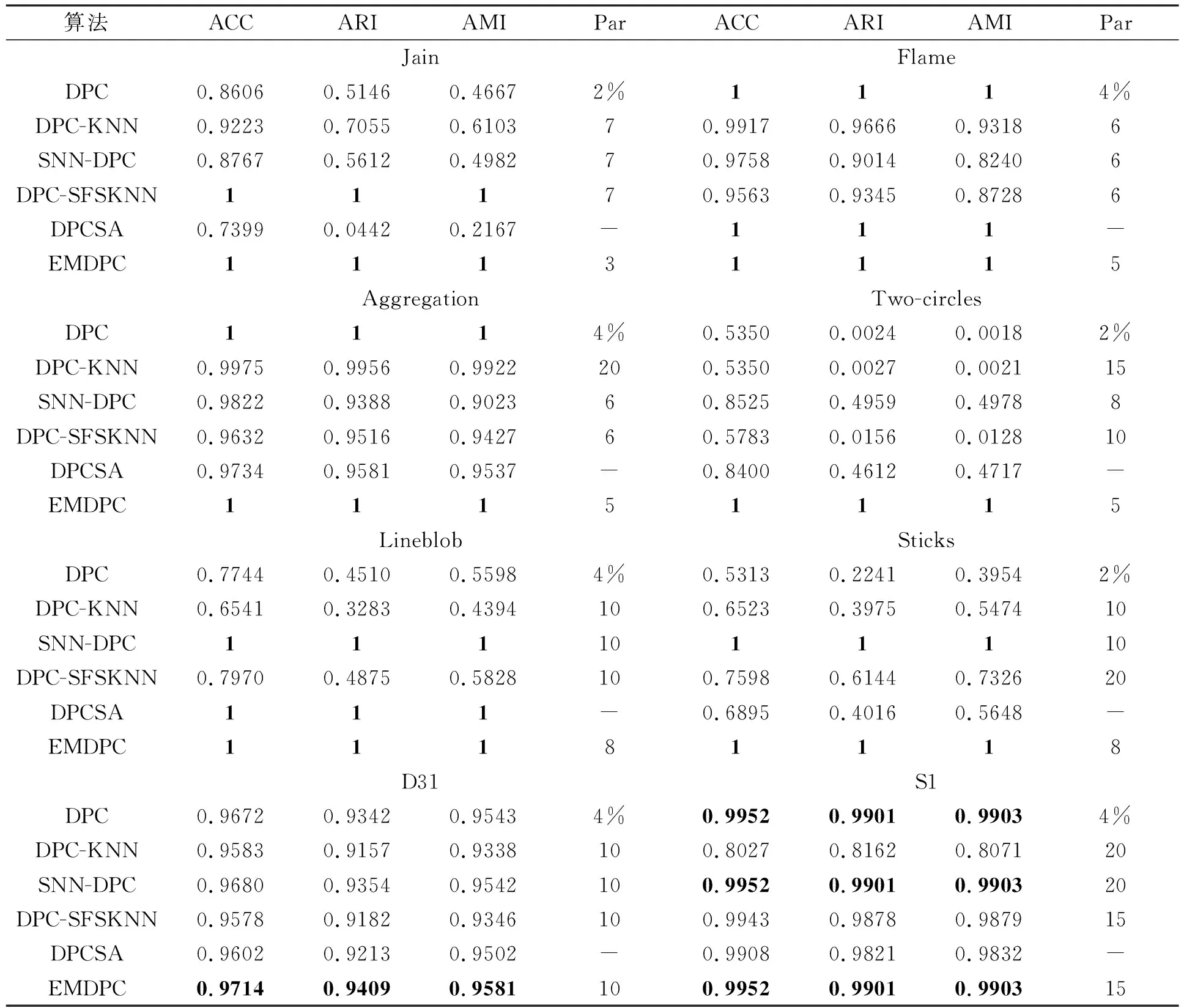
表3 8个人工数据集上的聚类结果

3.2.2 UCI真实数据集实验结果

为了进一步验证EMDPC的优良性能,将其与DPC,DPC-KNN,SNN-DPC,DPC-SFSKNN以及DPCSA在8个真实数据集上进行对比实验。这8个真实数据集来自UCI机器学习数据库(http://archive.ics.uci.edu/ml/),其详细信息见表2。

EMDPC与其他5种对比算法在真实数据集上的聚类结果如表4所示,其中加粗的数据表示最佳结果。可以看出,EMDPC在Glass、Heart、Ionosphere、Libras movement、Dermatology、WDBC以及Titanic上得到的聚类结果均比其他5种对比算法稍好些。这是因为这些真实流形数据集上的数据点密度不尽相同,其他对比算法容易将低密度簇中的数据点分配到标签不同的高密度簇中,从而导致不佳的聚类结果,而EMDPC通过电子分层模型缩小不同密度簇之间的密度差,使得低密度簇更容易被单独识别出来,从而不被误分类。在Ionosphere和Dermatology上,EMDPC取得6种对比算法中最高的ACC和ARI值,但其AMI值略低于DPC-SFSKNN的0.361 2和0.861 2,分别低了0.019 2和0.025 6。在Pima上,EMDPC的ACC值比其他5种对比算法略高,而DPC-SFSKNN取得了最高的ARI和AMI值。在Titanic上,EMDPC与SNN-DPC、DPC-SFSKNN、DPCSA取得一样的ACC值为0.776 0,然而EMDPC的ARI和AMI结果要比SNN-DPC、DPC-SFSKNN和DPCSA的结果更高。在Titanic上DPC和DPC-KNN的结果没有表示出来,原因是这两种算法在Titanic上取不到聚类中心,不能将其聚类,故无法给出对应的结果。

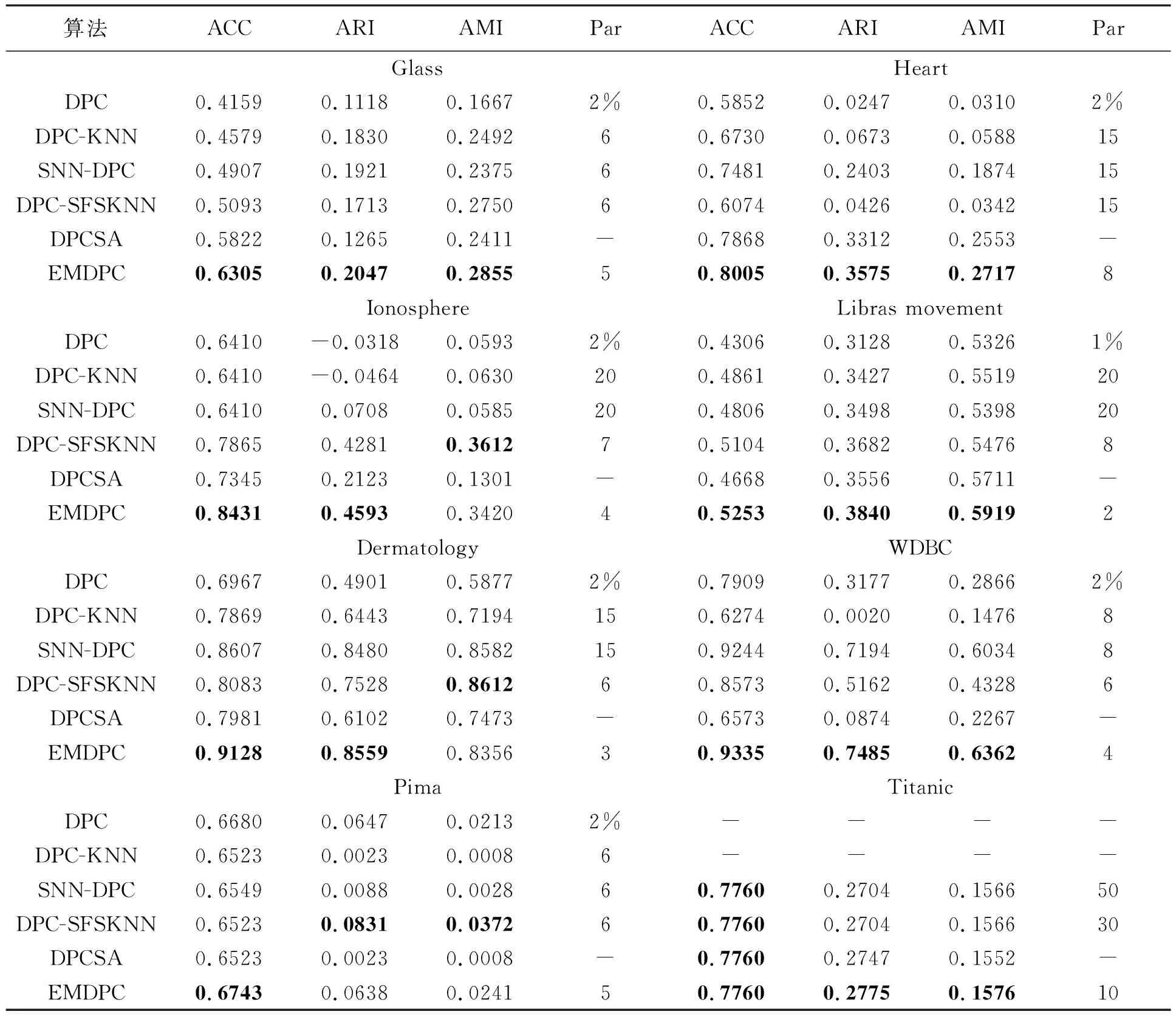
表4 8个真实数据集上的聚类结果

从表4中可以看出,EMDPC在大部分真实数据集上的实验结果要比其他5种对比算法更高。通过对比发现EMDPC的聚类性能在DPC的基础上提升15%左右,这充分表明了在基于电子分层模型的局部密度和凝聚策略作用下的EMDPC具有优良的聚类性能,能在密度分布不均的真实数据集上取得更为理想的聚类结果。

4 结束语

为了解决密度峰值聚类在密度不均匀的流形数据集上聚类性能不佳,由于人工干预增加聚类误差的问题,本文提出了一种基于电子分层模型和凝聚策略的密度峰值聚类算法EMDPC。基于电子分层模型计算得到的数据点局部密度能有效缩小数据间过大的密度差,从而更易识别低密度簇。由一种新的簇间相似度将子簇凝聚,其能通过数据自身的特点自适应得到聚类个数,无需人工干预。通过分层模型得到的局部密度与凝聚策略能有效解决DPC在密度分布不均的流形数据上聚类效果不佳的问题。在合成数据集和真实数据集上的对比实验进一步验证了本文算法的有效性和优越性。