融合B样条小波变换的图像铅笔画生成改进方法

李小强,朱玲艳,程 辉

(1.河南省数控应用技术工程研究中心,河南 郑州 450046;2.河南工业大学 信息科学与工程学院,河南 郑州 450001;3.英国赫特福德大学 计算机科学学院,赫特福德 哈特菲尔德 AL109AB)

非真实感绘制技术(Non-photorealistic rendering,NPR)主要是对艺术作品风格的仿真,表现出艺术特质,是计算机艺术中最活跃的分支之一[1]。其中,对铅笔画素描风格进行模拟受到研究学者的广泛关注,因此涌现出很多铅笔画绘制算法。这些算法主要包括图像轮廓和色调纹理两个部分。传统的边缘检测算法通常应用在图像的前期处理中,虽然易于实现,但是提取的图像边缘较为琐碎,易生成噪声点[2]。Lu等[3]提出二次卷积方法,生成的图像轮廓具有画家绘制铅笔画线条的交叉感,但是算法在提取轮廓时没有考虑到细节信息,尺度单一。黄志勇等[4]为了增强图像细节信息,提取图像不同层次的信息,并采用不同种类型的笔画绘制轮廓线条,但是由于细节信息过度叠加,导致结果图像中出现线条过重的效果。赵春晖等[5]为保留更多的细节信息,采用基于多尺度的小波变换方法模拟生成线条轮廓图。在色调纹理生成算法方面,刘磊等[6]提出自适应的高斯噪声图与线积分卷积(Line integral convolution,LIC)相结合生成铅笔画纹理的方法,但是这个方法得到的纹理方向不灵活多变。王冰[7]提出基于图像梯度的多向纹理人脸素描画生成算法,主要思想是提取出背景图像的边缘、阴影与根据背景图生成的多向纹理图、模糊图进行融合,生成素描图像。孔群晔[8]在分析了几种噪声模型的基础上,提出了一种新的混合噪声模型,替换了传统基于LIC的铅笔素描模拟方法中所采用的随机二值白噪声。使用混合噪声模型结合LIC模拟铅笔画局部走势纹理,能够较好地模拟生成类似真实铅笔画纹理,但是难以生成清晰可辨的纹理。Lu等[3]提出从真实铅笔画色调作映射得到色调合成结果,然而这种方法需要真实的铅笔画色调纹理,无法依靠计算机自动生成。孙丹丹等[9]提出应用运动模糊代替LIC模拟铅笔画纹理,虽然速度上有较大提高,但是方向单一。

通过对现有算法的分析比较,目前边缘提取算法主要存在两个方面的问题,一方面是提取的轮廓尺度单一,画面细节丢失;另一方面是提取的轮廓冗长,缺乏画家勾勒轮廓线条交叉的真实感。因此本文将B样条小波变换和二次卷积算法融合,生成的图像轮廓既具有交叉感又能够突出细节信息,轮廓更加平滑且不粗重。在色调纹理生成方面提出基于Meanshift分割在亮度图上添加高斯噪声生成噪声图、应用运动模糊分区域生成不同方向纹理图,生成的铅笔画纹理清晰,方向多变且减少了算法执行时间。

1 算法概述

算法根据输入图像生成具有铅笔画艺术效果的图像,主要包括轮廓图生成和多方向纹理图生成两个部分。首先,使用B样条小波变换和二次卷积获得两幅轮廓图,再分别对两幅轮廓图进行4层Haar小波分解,按照两幅轮廓图分解得到的各层对应高频系数取大值,低频系数取均值策略进行融合再重构,进而得到最终的轮廓图。其次,引入Meanshift算法分割图像,计算各图像区域内的梯度均值向量作为当前区域的纹理方向结合运动模糊的方法得到多方向纹理图。最后,轮廓图和纹理图通过点乘生成最终铅笔画图。图1为本文算法框架图。

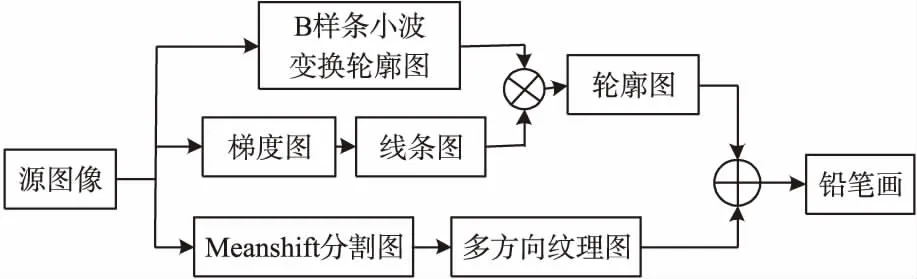
图1 本文算法框架图

1.1 轮廓图生成

1.1.1 B样条小波变换

针对目前边缘提取算法提取的轮廓尺度单一、画面细节丢失问题,采用B样条小波变换。因为B样条小波用于边缘检测时,其在边缘定位准确性和边缘连续性方面的性能均优于常见的微分算子[10,11]。

设θ(x,y)是二维小波平滑函数,且∬θ(x,y)dxdy≠0。沿x,y两个方向上的一阶导数

(1)

在进行小波变换时,图像f(x,y)的两个分量在尺度为s=2j(j=1,2,3,…)时的定义如下。

沿x方向

(2)

沿y方向

(3)

矢量形式可记为

(4)

梯度矢量的模值为

(5)

梯度矢量与水平轴的夹角为

(6)

由于图像的边缘是梯度矢量与水平轴的夹角方向上的模值的极大值点,因此,仅需检测A2jf(x,y)方向上的模M2jf(x,y)的极大值点,就可获得多尺度的边缘点。

1.1.2 二次卷积

在实际的铅笔画创作中,艺术家通常不会画一些很长并且不中断的曲线,线条通常在弯曲处或汇合处结束。因此在艺术家的作品中可以发现,两条线的汇合处或曲线的弯曲处会出现交叉现象,这是人手绘线条的一个重要特征。基于这一特征,运用二次卷积方法模拟线条交叉效果。

将输入图像转换为灰度图像,计算灰度图的梯度,得到梯度图。对梯度图采用二次卷积的方法实现线条交叉效果。

(1)首先计算图像梯度,得到梯度图G

(7)

(2)为了模拟铅笔画具有交叉感的笔画细节,对梯度图G分别进行8个方向的卷积,即0°、22.5°、45°、67.5°、90°、112.5°、135°、157.5°。形成8个方向的响应图

Gi=ξi*G

(8)

式中:ξi为第i个方向上的卷积算子,Gi为i个方向上的响应图,i={1,2,3,…,8}。

(3)计算8个方向上的响应图的最大值作为结果

(9)

式中:i为第i个方向,Ci(p)为像素点p在第i个方向的最大响应值,G(p)为像素点p的轮廓值。

(4)对得到的各个方向的响应图再次进行方向卷积,即

(10)

S=1-S′

(11)

对S′取反后即可得到铅笔画轮廓图S。

1.1.3 轮廓图像融合

B样条小波变换提取的轮廓细节与信息丰富,但是提取的线条粗重冗长。二次卷积算法生成的轮廓图细节信息丢失但是具有线条交叉这一特点。因此融合B样条小波变换与二次卷积算法能够弥补常用的边缘提取算法在提取轮廓时的不足。具体算法如下:

(1)分别对B样条小波变换提取的轮廓图W和二次卷积方法提取的轮廓图S用Haar小波实现四层分解。

(2)在低频系数中,分别提取W_A和S_A的第4层低频系数,并求均值。W_A表示轮廓图W小波分解后的低频系数,S_A表示轮廓图S小波分解后的低频系数。

(3)在高频系数中,提取W_H和S_H第4层中绝对值大的系数,W_H表示轮廓图W的H(4)|V(4)|D(4)第4层高频系数,S_H表示轮廓图S的H(4)|V(4)|D(4)第4层高频系数。

(4)根据(2)和(3)得到图像Y,通过小波逆变换获得的重构图像是最终的轮廓图。

图2显示了轮廓提取的结果。将图2(b)、图2(c)分别与图2(d)比较可以看出,图2(b)线条具有交叉感,但是在细节处不够清晰,图2(c)线条粗重不平滑,但是能够保留细节信息,而图2(d)线条完整清晰,平滑不模糊,且在交接处线条会有交叉。

图2 不同方法轮廓提取结果图

1.2 纹理图生成

1.2.1 图像分割

本文选择Meanshift分割算法,根据颜色聚类对图像进行分割。Meanshift算法是一种结合聚类理论的区域分割方法,其基本思想如下:设d维空间Rd中有n个样本点xi(i=1,2,3,…,n),(xi-x)为样本点xi与中心点x的偏移量,则在x点处的Meanshift向量为

(12)

式中:Sh半径为h的高维球区域,区域内的点为

Sh(x)={y∶(y-xi)T(y-xi)≤h2}

(13)

式中:k为落在高维球区域内的样本点的个数,则Mh(x)表示在高维球区域内的所有样本点xi与中心点x的偏移量的平均值。

引入核函数后,x点的Meanshift向量的形式为

(14)

式中:G(x)是核函数,h是宽带。

令初始点为x=yj,循环执行式(15)直至收敛即可得到对应的模值点y

(15)

将色度相同或相近的像素归为一类,达到图像平滑。对平滑后的图像进行区域合并,剔除细小区域,以限制最终分割的区域大小。

1.2.2 白噪声图的生成

在现有的铅笔画模拟算法中通常使用的是随机白噪声模型,但是这个噪声模型具有一定的局限性,如在暗处模拟产生的线条不细腻,易出现色块现象。为了改进这一问题,同时使生成的噪声图体现图像的明暗特点,在本文中提出了高斯噪声替换随机白噪声,此噪声表示如下

(16)

式中:Iv(x,y)为亮度图像素点(x,y)的亮度值;G(x,y)是高斯模型生成的噪声图;Inoise是依据亮度图产生的噪声图;T=k(1-Iv(x,y)),k是比例系数,k∈[0,1.0];P为随机数,控制噪声点产生几率。

根据文献[9]提出的算法生成的噪声图与本文算法生成的噪声图效果如图3所示。

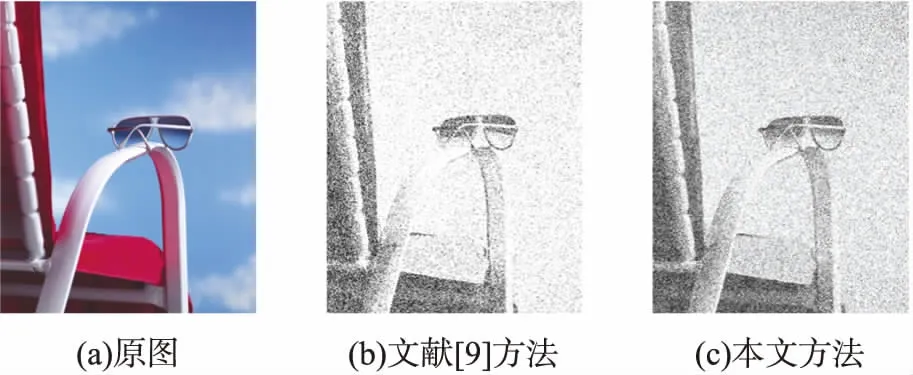
图3 不同算法噪声图效果

1.2.3 纹理图的生成

对铅笔画纹理的模拟在铅笔画生成方法中非常关键,LIC是一种模拟笔触纹理的重要方法,但是这种方法需要花费大量的时间,而且画家在实际的绘画中纹理走向是多变的,LIC无法灵活运用。运动模糊方法原是用来生产物体运动状态的效果,沿着特定方向对图像进行特定强度的模糊处理[9]。文献[9]对白噪声图进行运动模糊生成的效果与铅笔画纹理相似,且生成速度快,应用灵活,因此本文采用运动模糊生成铅笔画纹理。

在实际绘画过程中,画家会考虑物体的局部结构特征,并根据图像的亮度分布和层次感来决定笔触的走向,用细腻的笔触体现所绘制物体的方向特征,而不会使用单一方向进行绘制[8,12]。为了避免纹理方向单一问题,本文引入了Meanshift算法分割图像,针对不同区域利用运动模糊算法赋予不同的方向纹理。算法步骤如下。

步骤1首先对亮度图像进行卷积运算,得到亮度图像在水平和竖直两个方向上的梯度场,其计算公式如下

(17)

式中:Gx(i,j)和Gy(i,j)分别为亮度图像在水平方向和竖直方向的梯度。

步骤2在铅笔画绘制过程中,画家通常在同一个区域内使用相同的方向来绘制。因此本文通过计算一个区域内的所有像素的梯度均值作为区域的整体梯度。本文将求得的区域平均梯度作为每个区域运动模糊的角度。

步骤3创建运动滤波器,将白噪声图与预定义的运动滤波器生成的模块进行滤波运算,根据不同区域设定不同方向,就可以得到具有不同方向的纹理图。如图4显示的是Meanshift分割图与运动模糊的纹理图,从中可以看出,每个区域对应不同的方向纹理且纹理效果比较自然。

图4 运动模糊结果图

最终,将上述算法中得到的轮廓图与纹理图进行点乘运算,生成铅笔画效果图。

2 实验结果及分析

本文算法通过MATLAB 2018b编程实现。实验用计算机配置为Intel(R)Core(TM)i7CPU,主频3.79 GHz,内存16G,GeForce RTX 2080super独立显卡,64位Windows10系统。利用本文提出的算法对自然图像进行测试,从实验结果可看出,本文算法能得到较好的铅笔画效果。

本文方法得到的轮廓图结果与其他文献方法得到的轮廓图结果如图5所示。与文献[3]方法得到的结果相比,本文方法结果中会保留更多的图像细节,同时也能保留线条的交叉感;与文献[9]Kirsch方法得到的结果相比,Kirsch方法虽然可以勾勒出原图的轮廓,但是由于缺少对细节信息的处理,细节处的线条不够清晰,细节处虚而不实,而本文方法结果得到的轮廓线更加平滑清晰不粗重。

图5 本文轮廓图结果与文献[3]、文献[9]比较

本文提出在亮度图上添加高斯噪声替换随机二值白噪声,利用随机数控制噪声点,这样产生的纹理既有疏密效果,同时也有画面深浅的效果。本文方法得到的纹理图结果与其他文献方法得到的纹理图结果的对比如图6所示。从结果可以看出,文献[3]虽能生成较为理想的铅笔画结果,纹理也较为柔和,但缺少方向感。因为在真实绘画中,艺术家使用不同方向的笔触来描绘事物的结构特征。本文在Meanshift分割的基础上分析各个区域的纹理走向,以此生成方向多变的纹理。文献[9]由于在亮度较大的地方产生的噪声较少,应用运动模糊生成的纹理不明显不清晰,无法体现纹理疏密效果,且方向单一。文献[12]生成的纹理图线条凌乱,纹理方向感不足,纹理不够细腻。而本文方法在亮度较大的地方也能生成较多的噪声,在设置与文献[9,12]相同参数的情况下,应用运动模糊生成的纹理也是清晰细腻的。

图6 本文铅笔画结果与文献[3]、文献[9]、文献[12]比较

通过图7与表1的运行时间对比可看出使用运动模糊方法生成的纹理效果与运用LIC方法生成的纹理效果相似,但运用运动模糊方法方向灵活多变,且生成的纹理较LIC方法更清晰真实。同时在时间消耗上也可看出运动模糊方法生成纹理速度上更快。

图7 本文LIC方法结果与运动模糊结果对比

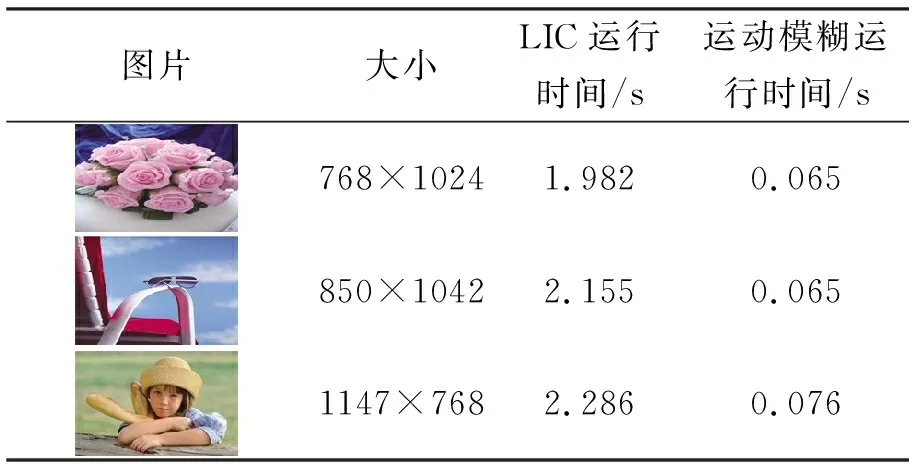
表1 LIC与运动模糊运行时间对比

3 结束语

针对现有铅笔画算法生成的轮廓细节丢失,线条不清晰等问题,本文提出融合B样条小波变换与二次卷积算法,得到的轮廓线条平滑完整,连通性好,且具有交叉感。常用的LIC方法由于使用随机白噪声生成的纹理不清晰,且执行速度慢。针对这一问题,本文提出在亮度图上添加高斯噪声替换随机二值白噪声,利用随机数控制噪声点,生成的纹理既有疏密效果,同时也能体现画面的深浅效果。应用运动模糊方法生成的纹理与LIC类似,但是算法速度有所提高,同时使用Meanshift分割,根据不同区域使用不同方向,避免了画面方向单一问题,更加有灵活性。实验证明,本文方法可以产生较好的铅笔画艺术效果图。