国家及地区的个数、人口、GDP 分布模型研究

孙二林，张为斌,2

（1.北京宸瑞科技股份有限公司，北京 100080；2.北京宸信征信有限公司，北京 100080）

“国家”是地理学的重要概念，根据联合国官网，目前全世界的国家个数是193 个[1]。除了“国家”以外，还有一些“地区”或“经济体”，如中国香港特别行政区、百慕大。关于地区的个数，不同的组织有不同的说法，如世界银行数据库中的地区个数是24 个[2]。国家和地区总数是200 多个。

国家和地区有三个基本变量：个数、人口、经济总量。国家和地区个数相对稳定，但有时也会发生变化，如1991 年苏联解体为15 个独立国家。一般认为，人口和GDP 在一定程度上符合幂律分布。奥尔巴赫（Auerbach）最早指出，城市规模分布可以用幂律分布近似表示；后来经过齐普夫(Zipf) 的进一步发展和完善，形成了城市规模分布的齐普夫定律[3]。从国内外现有文献来看，学者们采用齐普夫定律等方法，对中国城市规模分布进行了大量的实证研究，得出的主要结论争议比较大[4]。关于国家GDP 的分布，Corrado Di Guilmi 等人发现，在1960-1997 年期间，中等收入国家的人均GDP 符合幂律分布，其他国家不符合[5]。Narushige SHIODE 和Michael BATTY 发现，各国的人口、GDP、网站、超链接都不遵循幂律分布，只不过人口和GDP 的分布比Web 数据更接近幂律分布[6]。至于国家个数分布的研究则非常少。本文的目的就是探讨国家及地区个数、人口、GDP 的分布规律。

1.模型的基础

正态分布是自然界最常见的一种分布。例如，一个人口群体的智商；一组人的某科目考试成绩；实验中的随机误差，等等，均呈现为正态或近似正态分布[7]。布拉德福定律、齐普夫定律、洛特卡定律是文献计量学中最基本的三大定律，可以认为它们是一种分布规律的不同表现形式[8]。这种分布规律就是幂律分布。在经济学中，需求规律是在其他条件相同时，一种物品价格上升，该物品需求量减少的规律。需求规律可以用需求曲线表示，需求曲线是一种物品价格与需求量之间关系的图形。根据习惯，价格在纵轴，需求量在横轴，需求曲线是从左上方向右下方倾斜的曲线[9]。需求定律中的需求曲线也符合幂律分布。指数增长和Logistic 增长是最基本最常见的增长方式，它们能很好地刻画自然界和人类社会中很多物质量的变化规律。比如：生物种群的繁衍；人口的增加；树木的生长；国民收入的增长；传染病的传播；新产品、新技术的市场扩散等[10]。国家GDP的增长是指数增长，这方面的研究很多；各国GDP 的分布是否也是指数分布，这方面的研究较少。本文将尝试提出一种以指数分布为主、辅之以正态分布和幂律分布的分布模型。

当代法国政治社会学家莫里斯·迪韦尔热(Maurice Duverge)基于对政治的社会学认识,他首先把所有已存在过或存在着的国家分为两类:一是“未发展的国家”,二是“发展的国家”。莫里斯把现代社会的国家称之为发展的国家，并具体分为发达国家、半发达国家(认为称这类国家为发展中国家)、不发达国家三种国家类型。此外，有人按国家实力及国际地位把世界各国划分为超级大国、大国、中等国家和弱小国家[11]。世界银行于1978 年在世界发展报告中首次发布了国家收入分类标准以及人均国民总收入（GNI）指标的国家排序数据，将全球所有国家和地区按人均GNI 高低，划分为高收入国家组、中上等收入国家组、中下等收入国家组和低收入国家组[12]。以上分类中除了世界银行属于定量标准以外，其他均为定性标准。要研究国家及地区的个数、人口、GDP 分布，应该把定性标准定量化。

地理环境对人类有明显的限制作用。例如，科学技术迅速发展，促进了现代人类起源的研究，科学家们在化石、分子生物学、遗传学等方面不断取得新成果，总地来看，近几年获得的各项现代人类起源研究成果都明显倾向于“非洲起源说”[13]。为什么最早的人类起源于非洲，这难以用地理环境以外的原因解释。能量最低原理是自然界一切物质运动所必须遵循的自然法则，大到每一个化学反应，小到原子核外的电子运动，无不按照这一规律进行。齐普夫定律的理论基础是“最省力法则”[14]。这一法则也是能量最低原理的一种表现形式。人类受到地理环境和物理规律的限制，说到底是受到能量最低原理的限制。它使得人类像电子一样，按照能量从低到高的顺序填充地球表面乃至宇宙空间。能量最低原理也是本文的主要思想基础。

2.模型的假设

2.1 人口GDP 图

齐普夫定律可以描述单词在文献中以及城市在国家中的分布，文献可以看成是一维空间，国家内部的人口可以自由流动。但国家并非处于一维空间中，国家间的人口也不能自由流动。国家分布于地球表面，这是一个由经度、纬度、海拔高度组成的三维空间，但可以近似地看成是二维空间，因为海拔高度与地球半径的比值大约为1:1000，可以忽略不计。

人类从非洲出发，沿着经度变化（自西向东）和纬度变化（自南向北）两个基本方向迁徙，当然也可能沿着自西南向东北的方向迁徙，这个方向也可以分解为经度变化和纬度变化两个基本方向。在迁徙的路上，人类会组成人口越来越多的群体；另一方面，人类的人均GDP 又会越来越高。也就是说，“人口”和“人均GDP”也是人类进化的两个维度。人口越来越多的方向大致就是经度变化的方向，人均GDP 越来越高的方向大致就是纬度变化的方向。例如，印度、中国这样人口较多、较为贫穷的国家位于非洲的东方，而西欧、北欧这些人口较少、较为富裕的国家位于非洲的北方。既可以认为国家位于经度和纬度组成的二维地理空间中，也可以认为国家位于人口和人均GDP 组成的二维经济空间中。一个国家的人口和人均GDP 的乘积恰巧就是这个国家的GDP，因此在二维经济空间中分析国家的GDP 是最简单直接的方法。

经济学中的需求定律描述的人类的产品数量和价格之间的规律，从更底层角度来讲，人类本身也是地球的一种“产品”，同样也遵循地球的需求定律。我们可以绘制一张“人口GDP图”，其横坐标表示人口，纵坐标表示人均GDP，任何一个人群——包括家族、企业、国家、地区等——都可以用这张图上的一个点表示，点的横坐标与纵坐标的乘积就是这个人群的GDP。如图1 所示。

图1 人口GDP 图的示意图

在这张图上，按照幂律分布规律，人口和人均GDP 成反向变动关系，同一条双曲线（可以简化为从左上角到右下角的斜线）上的点表示GDP 相同的人群，双曲线的位置越高，线上的人群的GDP 也越高。例如，人群A 和B 位于同一条双曲线上，它们的GDP 相同；C 位于较低的双曲线上，它的GDP也较低；D 位于较高的双曲线上，它的GDP 也较高。

经济学中有两条重要的曲线：需求曲线和供应曲线，它们合起来构成了供需关系。一般来说，需求曲线从左上角向右下角延伸，而供应曲线从左下角向右上角延伸。在图1 中，人群A 和人群B 处于同一条需求曲线上，而人群C 和人群D 处于同一条供应曲线上。人群A 和人群B 的GDP 大致相同，人群C 和人群D 也有一个大致相同的变量，这就是人口。小而富的人群和大而穷的人群的GDP 总量差不多，小而穷的人群和大而富的人群的人口总量差不多。

2.2 九宫格

人口GDP 图既可以分为四格，也可以分为九格、十六格等等，其中最好的划分方法是划成九宫格。这是因为人类的脑力、体力等各种能力都服从正态分布，可以大致分为低水平的人、中等水平的人、高水平的人。一般来说，一个国家的人口多少基于组织能力，人均GDP 则基于科技研发能力。可以假定这两个能力服从正态分布，因此人口GDP 图的纵向和横向都可以分为低、中、高三档，由此构成九宫格，把所有国家和地区分为九种类型，如图2 所示。

图2 人口GDP 图中的九宫格

为方便起见，我们把九宫格编上号，从左下角到右上角依次是方格1 至方格9。如前所述，同一条从左上延伸到右下的斜线上的点的GDP 相同，斜线越高GDP 也越高，因此又可以把九宫格分为5 个GDP 等级，从左下角到右上角逐渐从1 级升高至5 级，它们的GDP 依次升高。与GDP 等级类似，还可以把九宫格分为5 个人口等级，从左上角到右下角逐渐从1 级升高至5 级，它们的人口依次升高。

2.3 假设的提出

至此，我们提出国家和地区的个数、人口、GDP 的分布的假设如下：

在以人口为横坐标、以人均GDP 为纵坐标的人口GDP 图中，所有国家和地区可以划分为九宫格，九宫格内的国家和地区个数、人口、GDP 符合指数分布，可以用三个指数函数表示。

指数函数一：国家和地区个数介于[27-M,29-M]之间，大致等于28-M，其中M 是从1 至9 的整数，是从左下角到右上角的方格序号；

指数函数二：假设方格1 的GDP 为1，那么其余各方格的GDP 介于[2N-2,2N-1]之间，其中N 是从2 至5 的整数，是从左下角到右上角的GDP 等级。或者，假设方格9 的GDP 为1，那么其余各方格的GDP 介于[2N-5,2N-4]之间，其中N 是从1至4 的整数，是从左下角到右上角的GDP 等级；

指数函数三：假设方格3 的人口为1，那么其余各方格的人口介于[2L-2,2L]之间，大致等于2L-1，其中L 是从2 至5的整数，是从左上角到右下角的人口等级。

3.模型的实证

3.1 数据及九宫格划分方法

我们用世界银行数据库中2000、2005、2010、2015、2018这五个年度的各国人口和人均GDP 数据进行验证[15][16]。该数据中共有217 个国家及地区，其中有20 多个中小国家和地区没有某年的人均GDP 数据，采用联合国数据[17]或世界银行数据库最接近该年的数据代替。还有3 个地区完全没有人均GDP数据，它们人口合计约为10 万人，即使忽略也影响不大。经过处理后有214 个国家和地区的数据。

五年数据的划分阈值及部分方格的具体国家如表1 所示。每一年都有两个人口阈值和两个人均GDP 阈值，它们把214个国家和地区划分为九宫格。请注意方格9 由美国独占，方格8 在2000 年、2005 年是空缺的，在2010 年以后巴西、中国依次进入方格8，2018 年中国独占方格8。

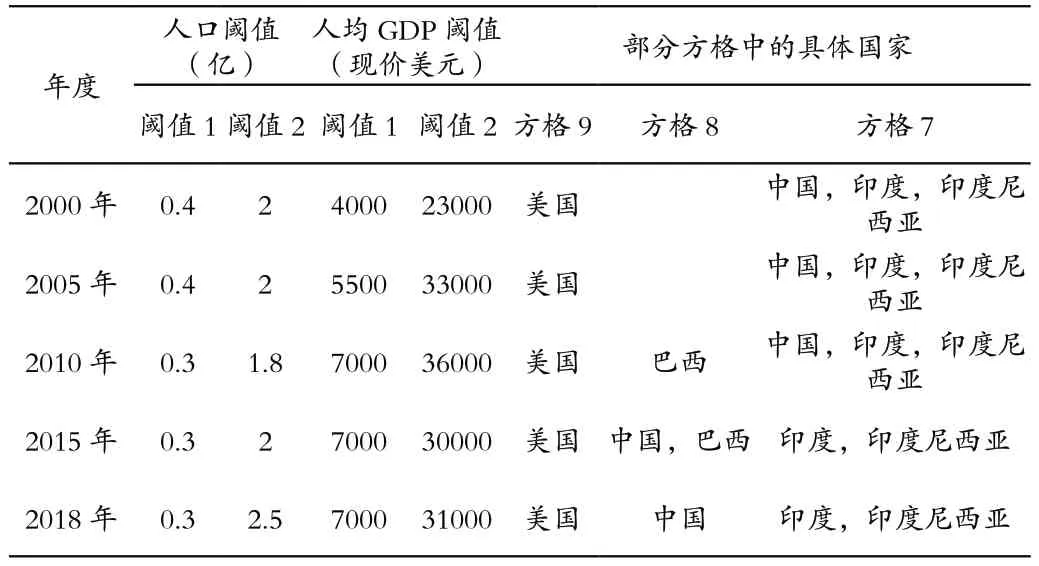
表1 五年数据的划分阈值及部分方格的具体国家

3.2 五年数据的验证情况

表2 是五年数据的验证情况。表格中有125 个背景为灰色的数值，这些数值可以验证实际数值是否符合指数函数。其中有15 个加粗的数值，它们是不符合假设的数值。2000 年、2005 年方格8 的各项数值为0，这是因为该方格是空缺的。

表2 五年数据的验证情况

表3 是五年总的验证情况，各年的准确率（相符数据个数与总数据个数的比值）在80%至96%之间波动，平均值是88%。

表3 五年总的验证情况

3.3 不符数据的原因分析

在15 个不符合的数据中，方格8 占了8 个，方格7 占了5个，不符合的数据主要集中在这两个方格。方格8 在2000 年、2005 年是空缺的，2010 年巴西进入方格8，但它的GDP、人口都达不到方格8 的指数函数值。直到2015 年，巴西、中国组成的方格8 才达到指数函数值。在2018 年，中国一国就可以使方格8 达到指数函数值。也就是说，2000 年、2005 年、2010 年的方格8 空缺或者数值偏低，是因为当时中国的GDP明显偏低。这段时间也是中国GDP 高速发展的时期，似乎是在填补方格8 的空缺，实际上2018 年中国一国就完全填补了这一空缺。方格7 的函数值与实际值差距较大，也是因为其中的国家——主要是印度——的GDP 明显偏低。目前印度的GDP 发展较快，可以预见在不远的将来方格7 的指数函数值与实际值就会相符。

从时间的角度来说，2010 年的准确率最低，这是因为2008 年爆发了全球经济危机，世界经济格局处于剧变之中，因此准确率较低。

由此可见，国家及地区的个数、人口、GDP 基本符合指数分布，但国家及地区处于动态变化之中，有的上升、有的下降、有的解体、有的合并，有时还会出现全球经济危机，因此会出现局部、短期不符合指数分布的情况。

4.模型的推论和意义

4.1 四个推论

根据以上三个公式可以推出世界上的国家和地区总数、人口总数和GDP 总值，它们可以用四个推论来描述。

推论一：根据指数函数一，用28-M 模拟九个方格中的国家和地区个数，累加起来得到255.5，这就是指数函数预测的国家和地区总数。实际上国家和地区总数为两百多个。

推论二：根据指数函数一可知，国家和地区的个数在1 倍、2 倍、4 倍之间来回波动。实际上，中国在从秦朝至今两千多年的历史中分分合合，绝大多数时间都是1 至4 个国家和地区。彼得-图尔钦利用历史动力学建立的模型也得出类似的结论：在一个模拟空间中相对稳定的帝国个数在1 个、2 个、4 个之间来回波动[18]。

推论三：根据指数函数二，假设方格9 的GDP 为1，把各方格的GDP 的范围[2N-5,2N-4]累加起来，得到GDP 总值的范围是[3.0625,5.125]，即方格9 的GDP 是GDP 总值的20%至33%。实际上在1960 年至2018 年的59 年中，方格9（即美国）GDP 占世界的比值介于21%至39%之间，平均值为29.4%[2]。

推论四：根据指数函数三，假设方格3 的人口为1，用2L-1 模拟各个方格的人口，累加起来得到49，也就是说，人口总数是方格3 的49 倍。实际上五年的总人口与方格3 人口的比值在49 左右来回波动，平均值是53.3。

可见，四个推论的数值接近于实际数值。

4.2 意义

本文的分布模型说明：地球上的200 多个国家和地区构成一个整体，国家及地区的个数、人口、GDP 是最重要、最基本的三个变量。这三个变量看似复杂，但它们都受地理和物理规律的限制，可以用简单的指数函数描述。在分析过程中应把正态分布、幂律分布、指数分布结合起来。本模型对于地理、历史、人口、经济、政治等学科的交叉学科的研究有启发作用，可以对一些老问题提出新解释，或者对未来作出预测。

例如，苏联解体的原因很多，从本模型的角度来说，苏联从1 个国家解体为15 个，这使得国家和地区总数更接近于255.5。又如，中国、印度之所以发展速度很快，从本模型的角度来说，是因为方格8 和方格7 空缺或者GDP 偏低。随着这两个方格的数值逐步达到指数函数值，GDP 增速也会放缓。