基于变工质模化方法的超临界CO2储能透平膨胀机相似特性分析

李祎然 ，李文 ,，常学煜 ，左志涛 ,，李辉 ，陈海生 ,4

（1中国科学院工程热物理研究所，北京 100190；2中国科学院大学，北京 100049；3毕节高新技术产业开发区国家能源大规模物理储能技术研发中心，贵州 毕节 551712；4中国科学院清洁能源创新研究院，辽宁 大连 116023）

随着工业科技化的日益推进，能源危机和环境污染问题亟待解决。节能减排、提高能源利用率、大力开发可再生能源利用技术必将成为增加能源供应和减少环境污染的重要措施[1]。但是，可再生能源面临着不稳定性和间歇性的问题，储能技术为之提供了良好的解决方案[2-3]。其中，超临界CO2(SCO2)储能技术因其热效率高、系统结构紧凑、环境友好等优点而备受关注。将CO2作为储能系统的工作介质，可以有效地将捕捉后的碳加以利用，有助于“碳达峰、碳中和”目标的实现[4-7]。

透平膨胀机是SCO2储能系统中用于做功发电过程的核心部件。由于SCO2透平膨胀机的设计条件为高温高压，较难获得，因此需要采用相似理论来组织试验。在对透平机械进行相似模化时，由于设计工质CO2较为昂贵，在进行模化试验时可以采用更为安全、易得的流体(例如空气)来代替。这就面临着透平机械相似模化试验中的一个重要课题——变工质下透平膨胀机的相似模化方法研究。

在解决变工质相似模化的问题上，刘立强等[14]针对氦透平膨胀机，除选取特性比U1/Cs为准则数外，还对不同圆周马赫数MU的范围内，采用分段选取准则数的方法，给定其影响范围。但是，该方法需要进行大量的理论计算，对于不同工质中绝热指数κ值的影响反映不足。胡朝斌[15]对向心式透平氦与空气的模化试验进行深入研究，认为只要保证特性比U1/Cs和膨胀比p＊1/p＊2相等就能达到较好地相似，缺乏准确的理论推导，分析方法需进一步细化。侯予等[16-17]认为圆周马赫数MU、膨胀比p＊1/p＊2、绝热指数κ与绝热效率ƞ之间为一种高度的非线性映射关系，故将人工神经网络(ANN)技术应用于透平膨胀机的性能转换研究中，从而解决变工质下透平膨胀机的性能转换问题。但是这需要以大量的试验数据作为训练样本才能将使ANN方法在透平膨胀机变工质的性能转换中更加可靠、有效，且以耗费大量的机时为代价。

除前面提及的无机工质之外，近些年来，有机朗肯循环(ORC)由于其可行性和可靠性而受到了广泛关注。在ORC透平膨胀机的有机工作介质之间的相似模化研究中，Wong等[18]提出了3种使用相似性概念的不同方法(理想气体法、可变压比法和恒定比转速法)，针对空气、R134a和R245fa进行了相似模化，但平均误差均在8%以上；White等[19-20]提出了一种模化方法以预测低温ORC中向心涡轮的适用性，针对静叶采用R245fa和甲苯进行验证，结果显示仅当流量保持亚音速并且涡轮雷诺数的偏差在±75%之间时，才可以依赖使用该相似性理论，有一定的局限性。

对于不同工质中运用到的相似理论，在前人的研究中，可以看出采用不同的相似准则存在不同的适用范围和问题。因此，运用合适的相似模化方法将不同工质的物性参数尽可能多地考虑进去，进行完善准确且切实可行的理论推导，将数值模拟与实验验证方法相结合是今后研究的重点。若能选择合适的相似理论，选择不同的工作介质，不仅能在一系列工况下准确预测特殊工质透平膨胀机的性能，而且可以在一定程度上扩大其工作范围，大大提高经济性和可行性。

本文采用因次分析法对变气体工质下透平膨胀机的相似模化进行研究，将实际气体工质的物性参数考虑在内，提出一种基于转速、进口总温、绝热指数和气体常数的新型变工质相似模化方法。利用计算流体动力学(CFD)方法对SCO2和空气在设计工况下的某透平膨胀机对该模化方法进行了数值验证和相似特性分析。

1 研究方法

1.1 变工质模化方法

相似模化理论是涡轮机械中的基本概念，合理运用该理论可以使设计人员无需重复整个设计和开发过程即可将涡轮设计扩展到不同尺寸或不同工作流体[21]。本文采用因次分析法确定透平膨胀机使用不同工质时的相似模化方法。方法流程如图1所示。

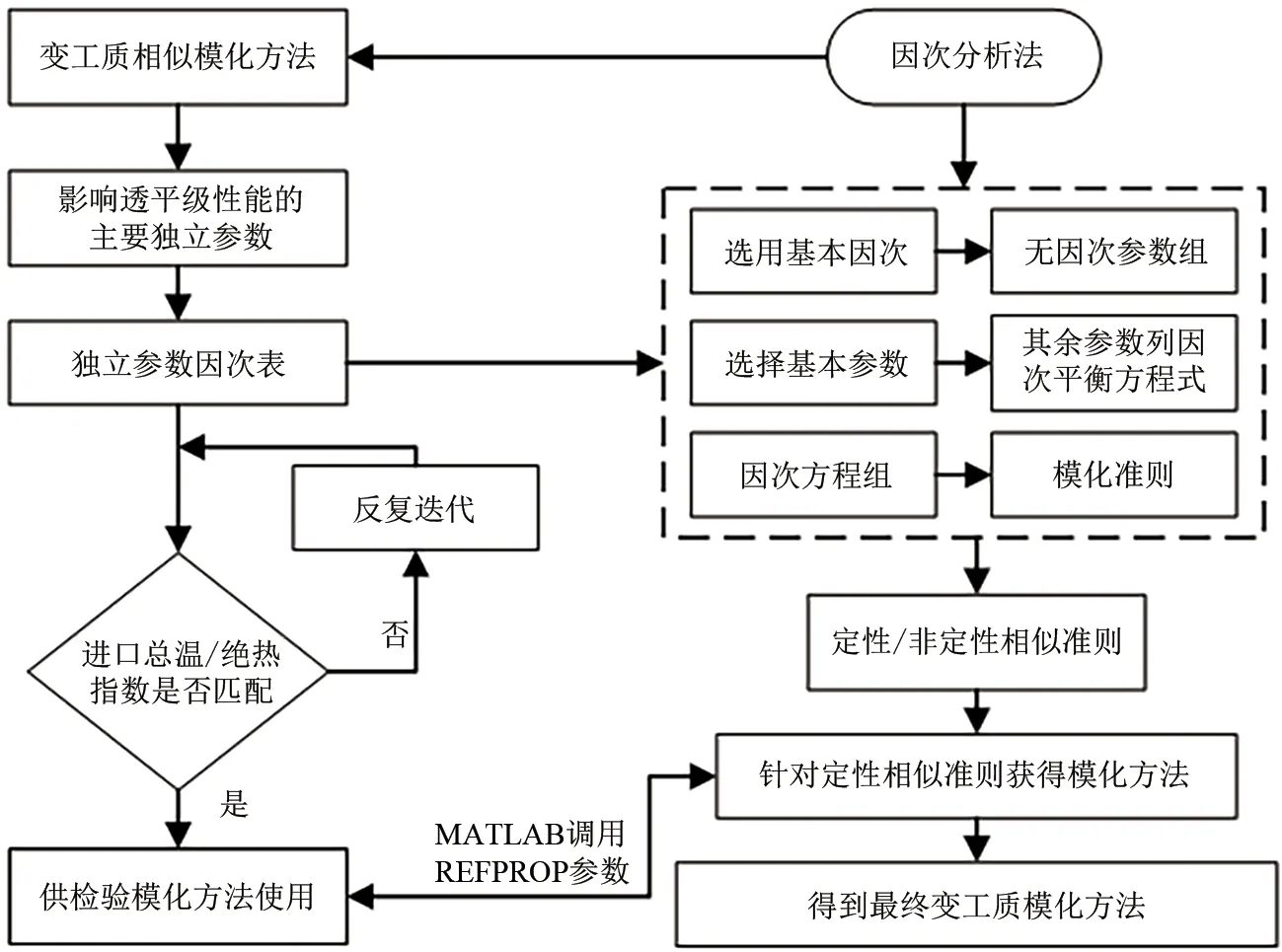
图1 变工质模化方法流程Fig.1 Flow diagram of different working fluids modeling method

首先，找出影响透平级特性的独立参数。假设透平级中的流动是一种稳定、有黏的绝热可压缩流动，影响级性能的主要独立参数见表1。

表1 影响透平级性能的主要独立参数Table 1 Main independent parameters affecting turbine stage performance

不考虑重力场g的影响，透平的级效率和功率可以表示成如下两个函数

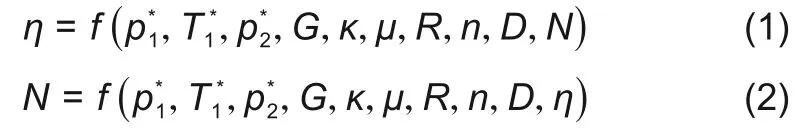
其次，选用长度(L)、质量(M)、时间(T)、温度(Θ)为基本因次，分析上述11个参数的因次，并得到无因次参数组π的数目i为

然后，选择基本参数p＊1、D、R、T＊1，利用其因次乘积幂，分别对其余参数列因次平衡方程式。以对p＊

2列因次方程式为例，求出无因次参数组π1

从而有

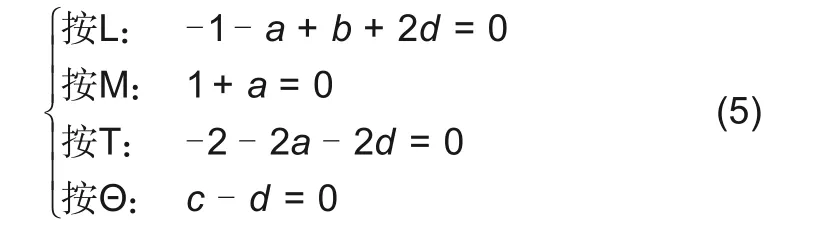
解得

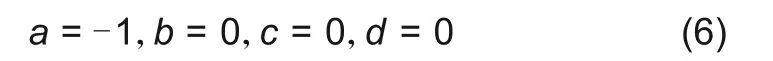
从而得到

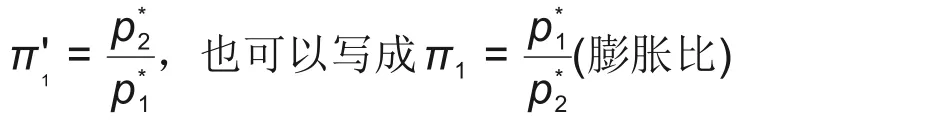
类似地，对G、μ、n、N列因次方程式，求出无因次参数组π2～π7。

于是得到所有的模化准则数，见表2。

表2 相似模化准则数Table 2 Similarity modeling criteria

经分析，选择保证定性相似模化准则π4值相等为本次模化方法研究的切入点。模化后的模型和模化前的原型分别以下标m和n表示。有

经过一系列的公式推导可得

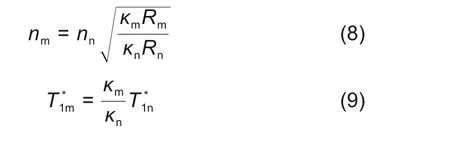
即转速n和进口总温T＊1在模化前后的对应转化关系。

考虑到实际气体的绝热指数κ随温度不断变化，采用MATLAB编程调用REFPROP数据库中的参数。为建立便捷的模化实验条件，选用进口参数为特征参数，反复迭代，得到对应互相匹配的绝热指数κ和进口总温T＊1。至此，得到了变工质透平膨胀机相似模化方法。

1.2 CFD数值验证模型

采用CFD计算模型对提出的变工质相似模化方法进行验证，数值模拟软件为ANSYS CFX。选用NASA Technical Paper 3514[22]中公布的向心透平模型。该向心涡轮实验的主要涉及参数见表3。图2(a)为该向心涡轮结构与网格的示意图。数值模拟采用SST湍流模型，进口湍流度为5%。工作介质为空气。进口边界条件给定总温、总压和气流角，出口边界条件给定平均静压。通过网格无关性验证确定导叶网格节点数约50万，叶轮网格节点数约90万。求解中残差值为10−6。

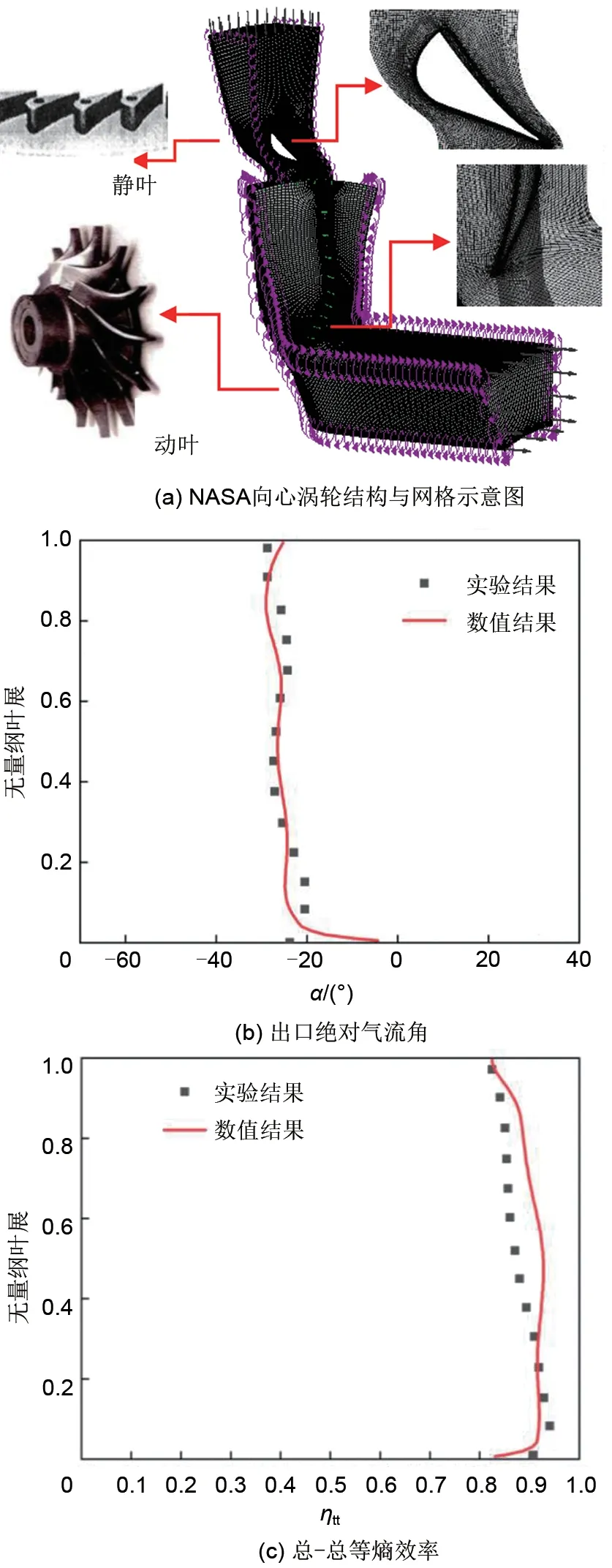
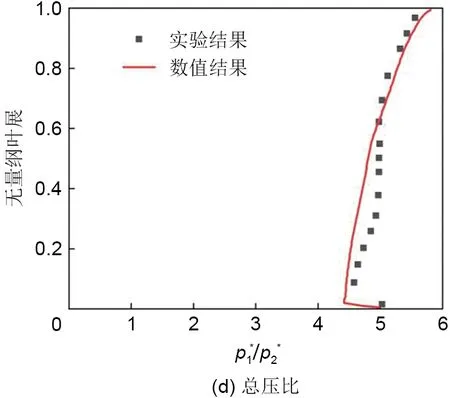
图2 NASA向心涡轮内部流场验证Fig.2 Verification of internal flow field of NASA radial turbine

表3 数值验证向心涡轮主要涉及参数Table 3 Main parameters of radial turbine involved in verification

表4给出了数值计算和实验结果的总体气动参数对比。可以看出，数值计算结果基本符合实验测量结果，但是仍存在一定的误差(均小于5%)，这是由于数值计算中引入的一些理想化假设造成的。例如，未考虑叶片背部间隙带来的影响；壁面绝热边界，动静叶交界面周向平均处理等[23]。此外，数值模拟本身也会存在一定的数值误差。

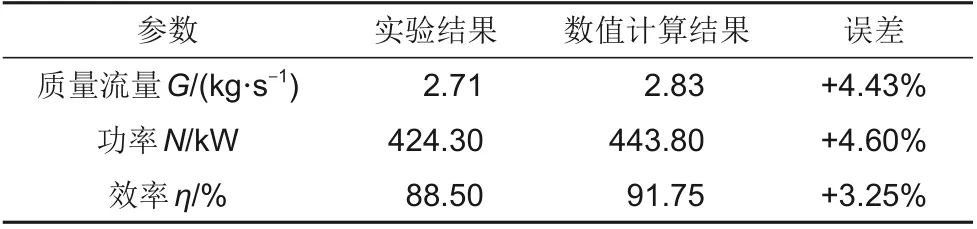
表4 总体气动参数对比Table 4 Comparisons of overall aerodynamic parameters

图2(b)～(d)为叶轮动叶出口截面周向平均气动参数沿展向分布的对比。从图中可以看出，数值计算与实验的出口绝对气流角、总-总等熵效率及总压比分布均吻合较好。由总体参数和流场细节对比，可以认为CFX对向心涡轮总体性能参数计算和内部流场分布预测具有较高精度。另外，多位学者也利用CFX对SCO2透平进行过详细模拟[24-27]，均具有较高的可靠性。综上，本节对向心透平的详细模拟为本文变工质模化方法应用及膨胀机特性分析提供了良好参考依据。

2 空气模化SCO2 膨胀机相似特性分析

以某向心透平为研究对象，采用1.1节所提出的变工质相似模化方法对其可靠性进行数值验证。图3为该向心透平模型及网格。选用CO2、空气两种工质进行计算，均采用实际气体的真实物性参数。为了利用空气对SCO2进行相似模化，并验证该模化方法在宽物性的变化范围内仍具有较高的准确度，选取高温度(873.15 K)、高压力(18 MPa)情况下的SCO2设计工况。选取一个CO2过渡工况作为纽带和桥梁，以实现空气设计工况和SCO2设计工况的相似模化转换。表5为利用该模化方法得到的参数。

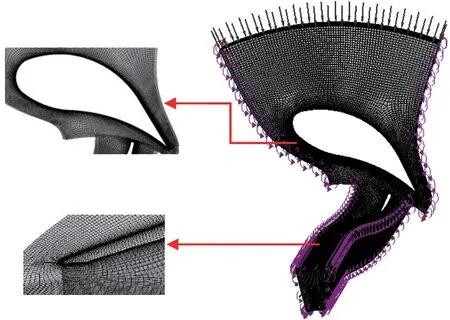
图3 向心透平模型及网格Fig.3 Radial turbine model and mesh

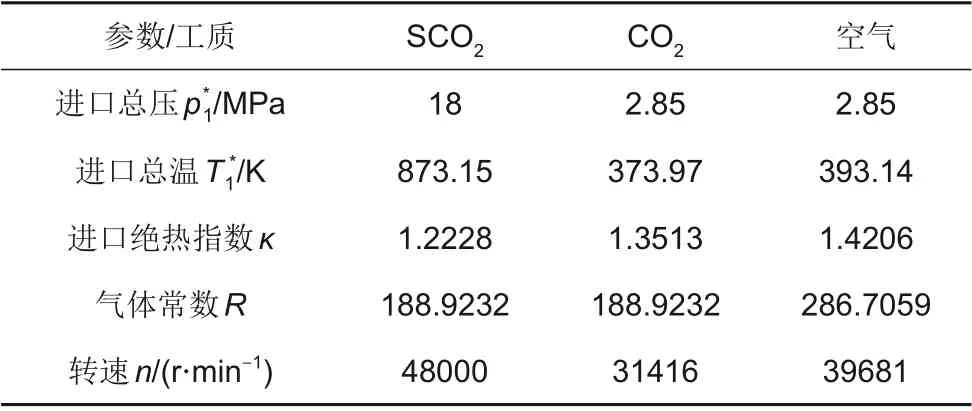
表5 应用变工质方法后的数值计算参数Table 5 Numerical calculation parameters with different working fluids method

2.1 变工质相似模化方法对总体性能参数预测效果分析

针对该模化方法，对两种工质下的透平膨胀机进行数值计算得到的总体性能参数见表6。对于过渡工况CO2和空气，总总等熵效率相对于SCO2的模化误差分别为0.73%和0.26%；对于1.1节得到的模化准则折合流量π2，过渡工况CO2的模化误差为4.69%，空气为4.09%；对于折合功率π5，过渡工况CO2的模化误差为−3.02%，空气为−1.41%；对于特性比U1/Cs，需要提醒的是，此参数并不是本文的模化准则之一，只是前人采用的模化准则中多含有该项，于是借此验证模化方法的准确性，过渡工况CO2的模化误差为3.51%，空气为2.17%。从图4的雷达图中可以更加直观地看出，该方法对于过渡工况CO2和空气工况的相似模化效果显著。

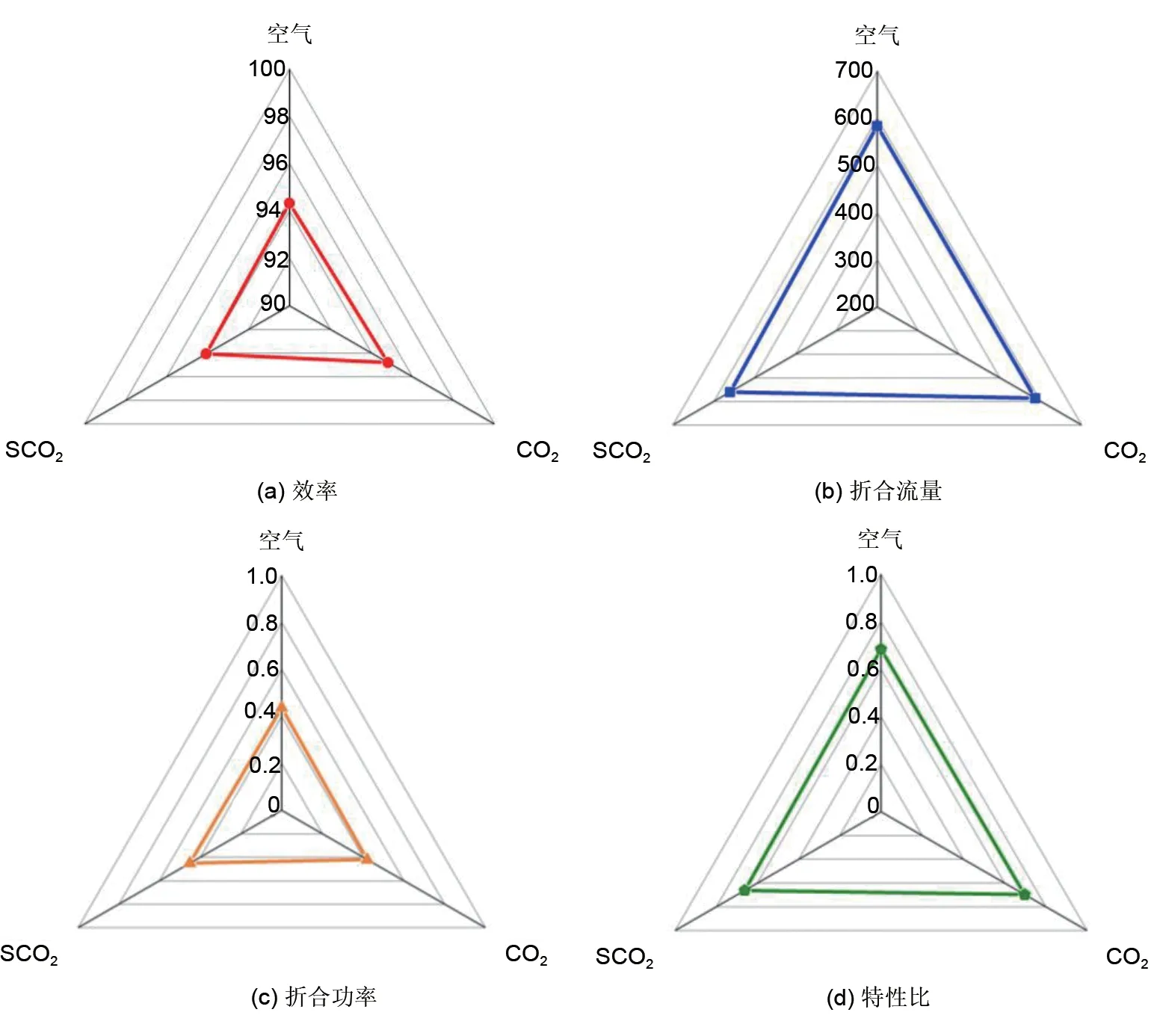
图4 数值结果对比雷达图Fig.4 Comparison of numerical results with radar maps

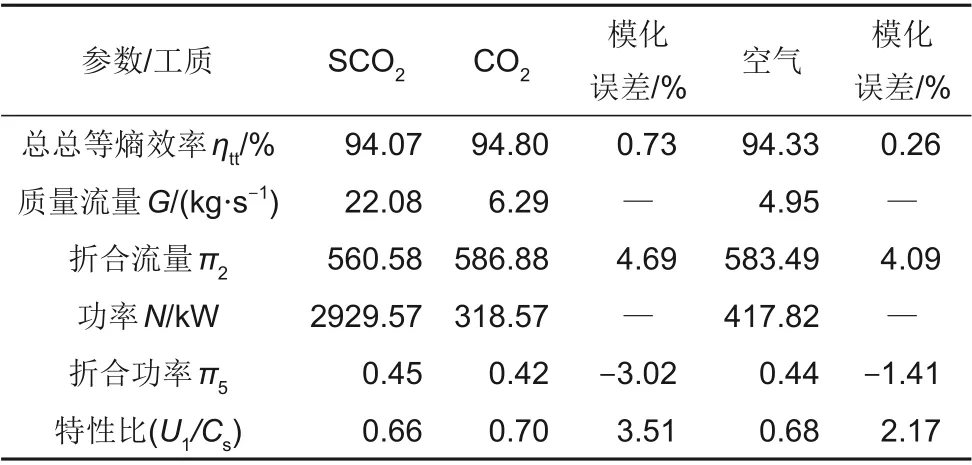
表6 数值计算结果Table 6 Numerical results

2.2 变工质相似模化方法对内部流场结构预测效果分析

为探寻该模化方法对于内部流场预测的准确性，对SCO2、CO2、空气3种工况下50%叶高处的相对马赫数分布和速度分布进行对比(图5、图6)。

从图5、图6可以看出，对于空气工况和过渡工况CO2，除在动叶出口有轻微差别外，单级相对马赫数云图分布和速度云图分布基本与SCO2工况吻合，表现出良好的模化效果。观察动叶进口速度矢量分布，气流攻角为零，符合设计工况的要求，说明该模化方法对于预测变工质下的普通设计工况和超临界设计工况都具有较高的准确性，并且在宽的工质物性变化范围内具有较高的适应性。

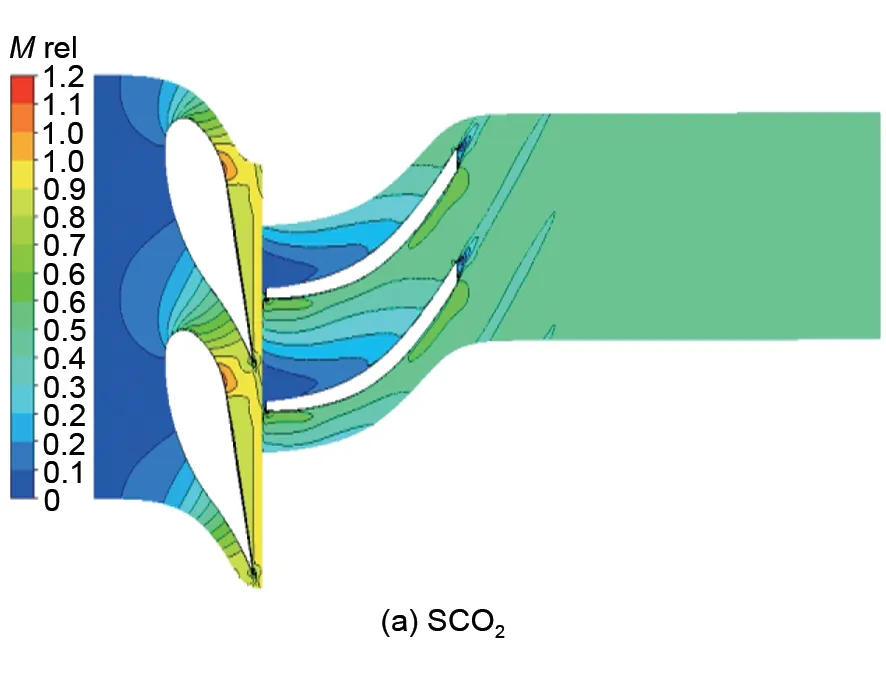
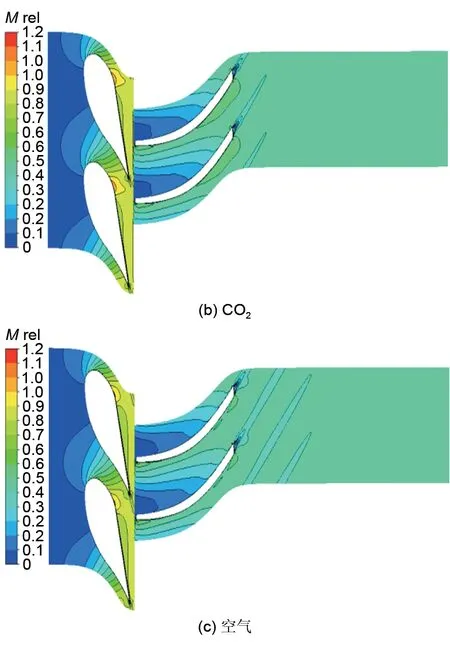
图5 相对马赫数分布云图(50%叶高)Fig.5 Stage contour of relative Mach number at 50%span

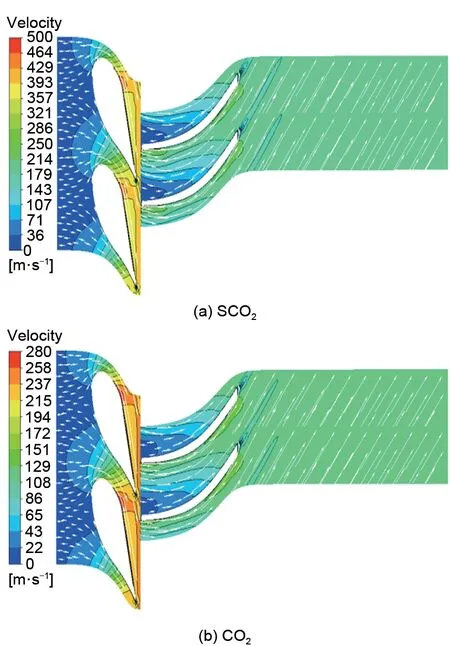
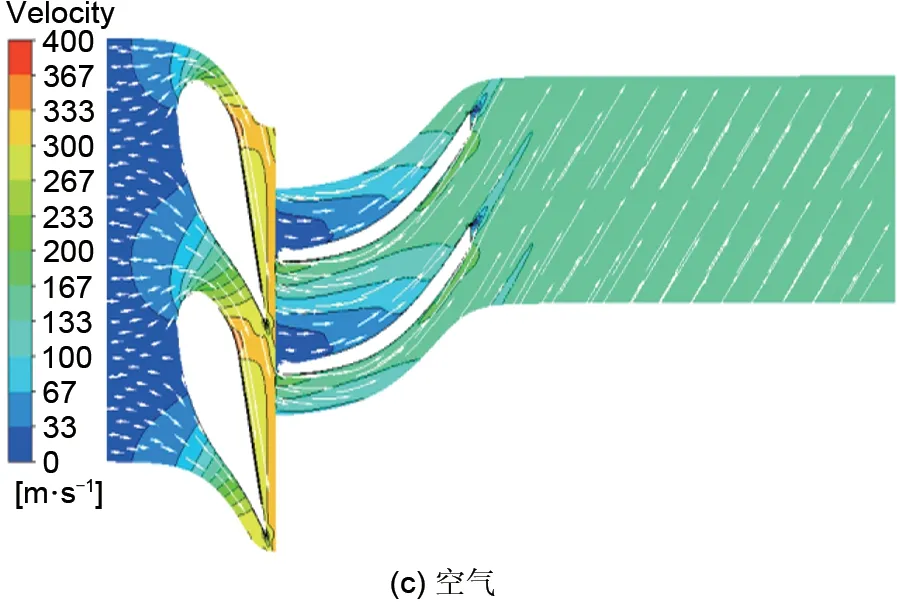
图6 速度分布云图(50%叶高)Fig.6 Stage contour of velocity vectors at 50%span

除此之外，为进一步验证在该模化方法下，空气模化SCO2工况的准确性，对两者静叶和动叶的负载情况(图7)进行了比较。从图7来看，在静叶无量纲流向0.7～1.0位置处，压力分布出现轻微差异，动叶在全范围无量纲流向位置内压力分布均基本吻合。整体来看，可以认为，两者静叶和动叶的负载情况基本相似，该方法对于空气模化SCO2工况具有较好的效果。

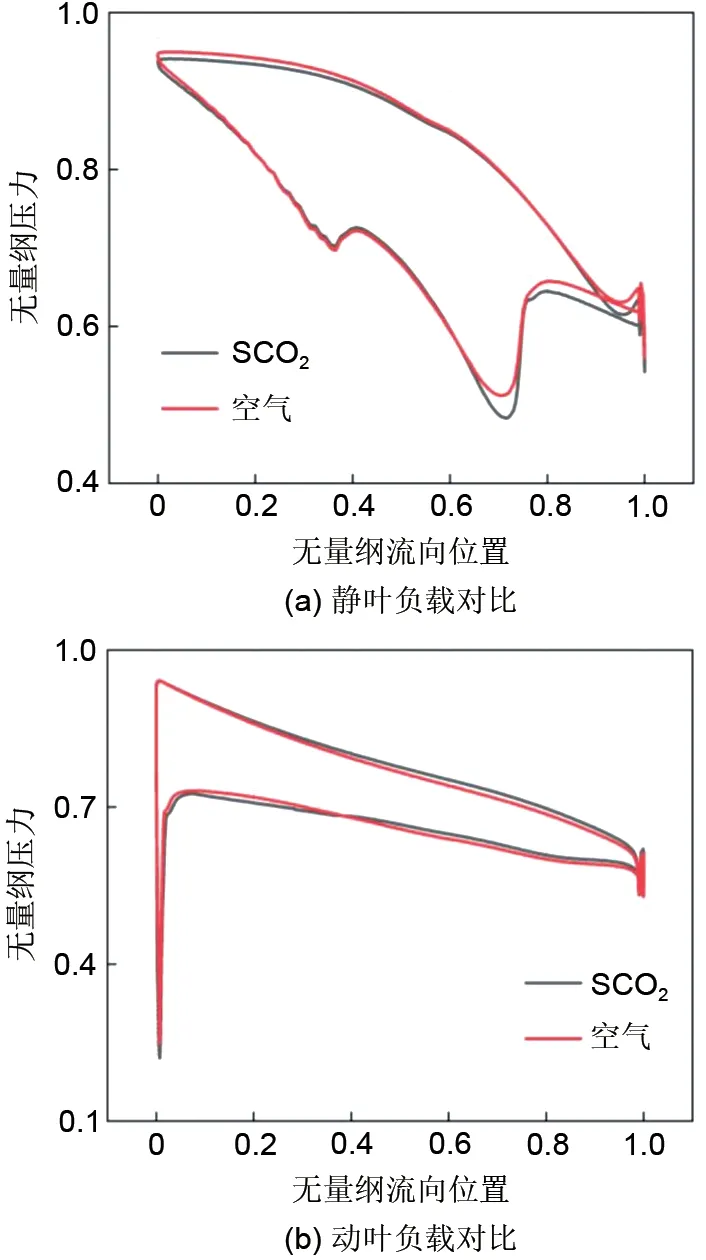
图7 静叶/动叶负载情况对比(无量纲压力为实际压力/110%压力上限)Fig.7 Comparisons of stator/rotor blade loading(The dimensional pressure is the actual pressur 110%pressure upper limit)

3 结 论

本文提出了一种新型变工质相似模化方法，并基于该方法采用空气对SCO2透平膨胀机进行了相似模化研究，取得了显著的效果。具体结论阐述如下。

（1）采用因次分析法得到7组相似准则数群，推导提出了转速和进口总温与实际气体物性参数(气体常数、绝热指数)的变工质透平膨胀机相似模化方法，为组织模化实验提供了一种较为便捷的转换关系。

（2）采用SCO2、CO2、空气对该模化方法进行了数值验证。结果显示，从总体性能参数来看，模化效果较为理想。对于空气工况，总-总等熵效率相对于SCO2的模化误差为0.26%；关于折合流量、折合功率和特性比，误差分别为4.09%、-1.41%和2.17%。

（3）从内部流场结构来看，3种工况下的相对马赫数分布和速度分布高度相似，该模化方法能够很好地预测设计工况下的流场情况。

总的来说，本文提出的变工质模化方法对于空气模化SCO2具有很好的效果，适用于高温度(873 K)、高压力(18 MPa)下的SCO2储能系统与其他工质工况的相似性转化。对进一步研究特殊工质透平膨胀机特性有一定的指导和借鉴意义。

符号说明

C—— 绝对速度，m/s

D——叶轮特征直径，mm

G—— 质量流量，kg/s

h—— 焓，J

M——马赫数

N——功率，W

n—— 转速，r/min

p—— 压力，Pa

R—— 气体常数，J/(kg·K)

Re——雷诺数

T——温度，K

U—— 圆周速度，m/s

W——相对速度，m/s

Z—— 叶片数目

κ—— 绝热指数

μ—— 动力黏度，N·s/m2

ƞ—— 绝热效率

Ω—— 反动度

π—— 无量纲相似准则数

Ф—— 流量系数

下角标

m——模化后

n—— 模化前

rel—— 相对

s—— 等熵过程

tt—— 总总

1—— 静叶进口

2—— 动叶出口

上角标

＊—— 总