隔舌安放角对泵作透平正反模式下水力性能的影响

袁志懿 ，张永学 ,2，祁紫伟

（1中国石油大学(北京)机械与储运工程学院，北京 102249；2海南医学院国际教育学院，海南 海口 571199）

抽水蓄能技术是一项成熟且被广泛应用的物理储能手段。传统抽水蓄能系统具有大规模与大容量的特点，其发展受到地理条件选址以及开发成本的限制[1]。近年来随着分布式储能的发展，低成本、建设周期短的微型抽水蓄能技术逐渐成为研究热点。由于离心泵具有运行维护成本低、广泛易得等经济技术优势，泵作透平在微型抽水蓄能系统中(<100 kW)有较高的经济效益和应用价值，尤其是在农村或偏远地区[2-3]。Kusakana[4]对4 kW的抽水蓄能微电网与4 kW柴油发电微电网的运行成本进行比较分析，发现抽水蓄能系统的日常成本降低71.3%。该学者[5]又对南非一个农场的8 kW抽水蓄能系统建模分析，指出其电力成本降低68.44%，投资回收期5.9年。

理论上不同系列的泵都可作为透平运行[6-7]，但实践中发现，直接采用泵反转作透平的方式，其效率往往较低，不能很好地满足能量回收的要求，严重制约了泵作透平的应用。为了提高泵作透平的效率，许多学者对其主要过流部件展开了内流分析与优化研究。Štefan等[8]对泵作透平的正反模式性能进行了模拟预测和实验验证，发现透平模式最佳效率点的流量高于泵模式最佳效率点流量的27%，此时透平的必需水头比泵扬程高41%，在小流量情况下透平容易受流动分离的影响使效率急剧减小。Ghorani等[9]使用熵产理论研究了泵作透平内流场的水力损失，发现叶片进口冲击损失、液流角与叶片出口角不匹配，以及转轮内部的流动分离是造成不可逆损失的主要原因。Dai等[10]研究了转轮进出口角、出口宽度和包角等结构参数对低比转速离心泵的泵模式和透平模式性能的影响，发现当转轮结构参数改变时，与透平模式的必需水头变化相比，泵模式的扬程变化更显著，增加转轮出口角会使两种模式的水力效率降低。Singh等[11]研究了转轮进口部分修圆对透平性能的影响，通过实验发现修圆可以减小水力损失并使效率提高2%。杨孙圣等[12-13]对泵作透平展开了系列研究，发现增加叶片进口安放角会使透平小流量工况的效率降低，大流量下的效率增加。另外使用长短叶片可以改善透平内部流动，减小转轮内流动损失。严健儒等[14]选取了转轮的4个结构参数(叶片出口直径、出口宽度、出口安放角和叶片包角)进行正交设计优化，研究表明叶片出口直径对泵模式和透平模式影响最大，优化后的出口直径增大，出口安放角减小，包角增大，出口宽度不变，此时水泵设计工况效率提高1.06%，水轮机设计工况效率提高1.62%。

除了转轮结构，蜗壳也是受到广泛研究的优化对象。吕剑渊等[15]采用数值模拟方法研究了隔舌安放角对泵运行工况的影响，结果表明适当增大隔舌安放角可以减小蜗壳的压力脉动以及隔舌处的回流，抑制能量耗散，最佳效率可提高14%。史广泰等[16-19]使用数值模拟方法对蜗壳结构对液力透平流动影响开展了大量研究，研究发现当透平蜗壳的进口周向截面直径较大时，隔舌处的压力脉动会增加。适当减小蜗壳进口截面直径可以使效率增加1.83%，此时转轮内压力分布与径向力分布最为均匀。当蜗壳断面形状为梯形时效率最高。Arani等[20]通过实验研究了隔舌形状对低比转速离心泵反转性能的影响，通过设置不同的隔舌延伸长度和倾角，分析发现，延伸隔舌长度并倾斜−10°可以使偏离工况效率增加8%，出力增加32%。Morabito等[21]通过数值模拟同样发现增加隔舌长度和适当减小倾角可以提高透平效率，其原因在于转轮进口液流角的改变。

通过以上文献可以发现，在泵作透平的内流分析与结构优化中，隔舌对其正反模式的水力性能有着显著影响。然而已有研究大多只关注结构参数变化对单一运行模式下流场的影响，缺乏对两种模式运行的整体分析。鉴于此，本文以数值模拟为主，分析了不同隔舌安放角对低比转速离心泵作透平正反模式运行下的泵扬程、透平必需水头、效率等的影响规律，结合熵产诊断方法，讨论了引起效率变化的根本原因，为泵作透平的选型与设计优化提供参考。

1 数值计算方法

1.1 模型与网格

本文使用一低比转速离心泵作为对象进行研究，其泵模式的额定转速为2900 r/min，额定流量为12.5 m3/h，额定扬程为78 m，比转速为23.7。模型泵主要结构如图1所示，为了使数值模拟更准确，考虑圆盘损失与泄漏的影响，计算域包括间隙腔体A和B。图2为转轮与不同隔舌安放角的示意图，模型泵的主要结构参数值见表1。蜗壳的基圆直径为248 mm，蜗壳进口宽度为12 mm，蜗壳出口直径为32 mm。由于在低比转速离心泵的设计中，隔舌安放角的建议取值范围是0°～15°[22]，因此本文的隔舌安放角在0°～15°内取3个值，并在范围外等距取1个值，设置4种不同的隔舌安放角分别为5°、9°、15°和20°。此处的9°为实验泵模型的隔舌安放角数值。

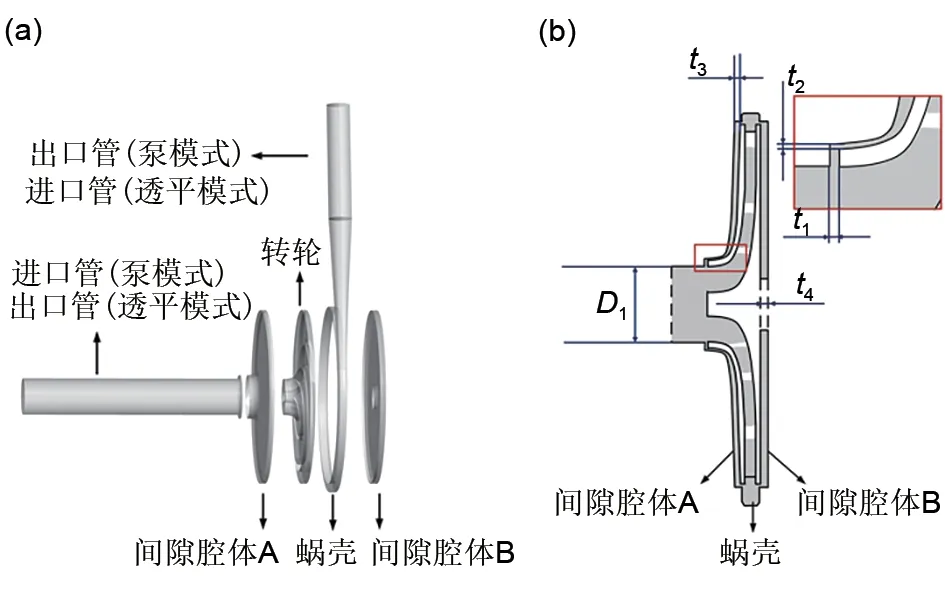
图1 低比转速离心泵模型Fig.1 Schematic of low specific speed centrifugal pump

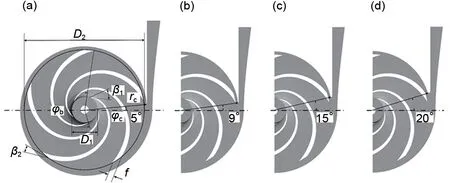
图2 转轮与蜗壳截面结构Fig.2 Geometrical details of runner and volute

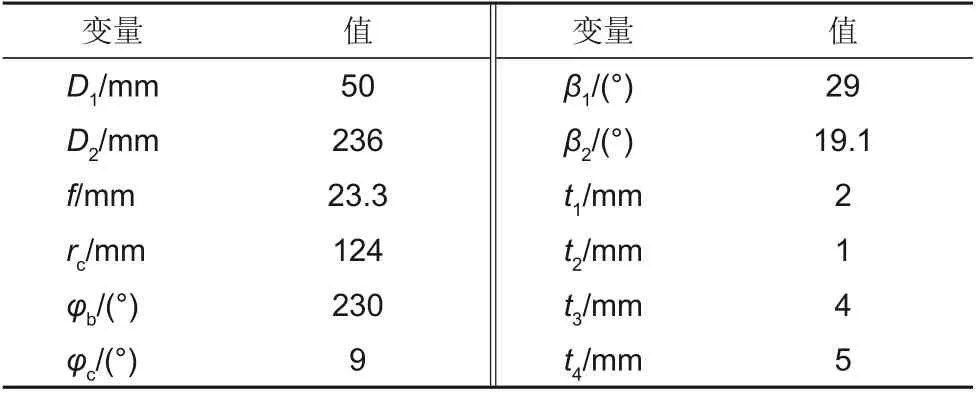
表1 泵结构参数Table 1 Geometric parameters of pump

为了减少计算时间，提高计算精度，采用ICEM软件对模型泵进行结构网格的划分，转轮与蜗壳的网格情况如图3所示，在叶片处添加边界层网格，第1层网格高度设置为0.003 mm，边界层网格增长率为1.3，平均Y+为1.8。隔舌处边界层设置与蜗壳壁面一致，第1层网格高度为0.1 mm，平均Y+为33。

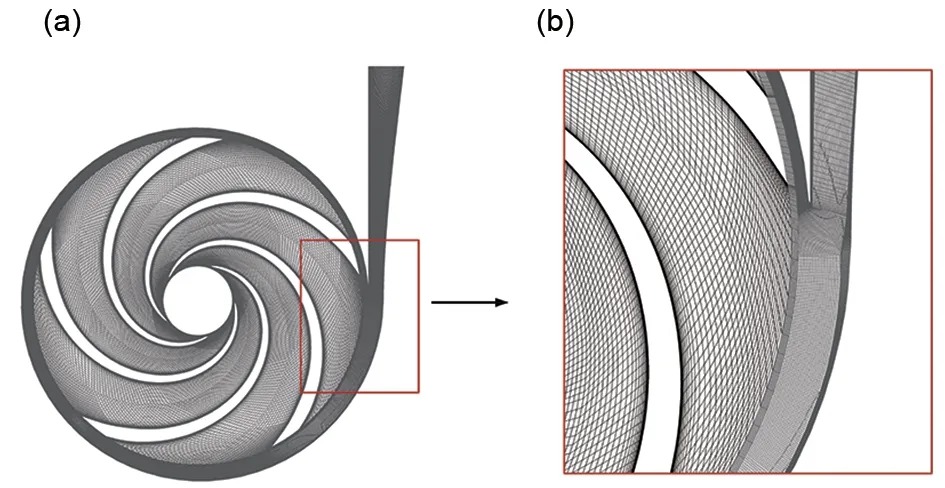
图3 转轮与蜗壳的结构网格划分Fig.3 Structured mesh of runner and volute

1.2 性能参数

本文使用泵扬程、透平必需水头、效率以及功率损失来评价泵作透平正反运行时的水力性能。在泵模式运行时，扬程Hp和效率ηp的计算式为

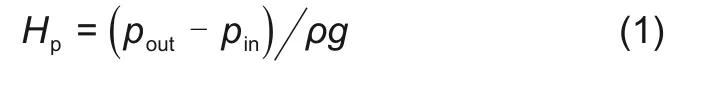
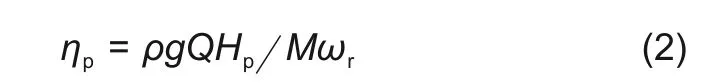
式中，M为扭矩，N·m；Q为流量，m3/s；ρ为密度，kg/m3；ωr为角速度，rad/s。

在透平模式运行时，必需水头Ht的计算公式与泵扬程计算一致，只是进出口的位置变化，透平效率ηt=1/ηp。

使用H＊表示无量纲扬程或无量纲必需水头

式中，d为转轮出口直径，m。

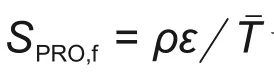
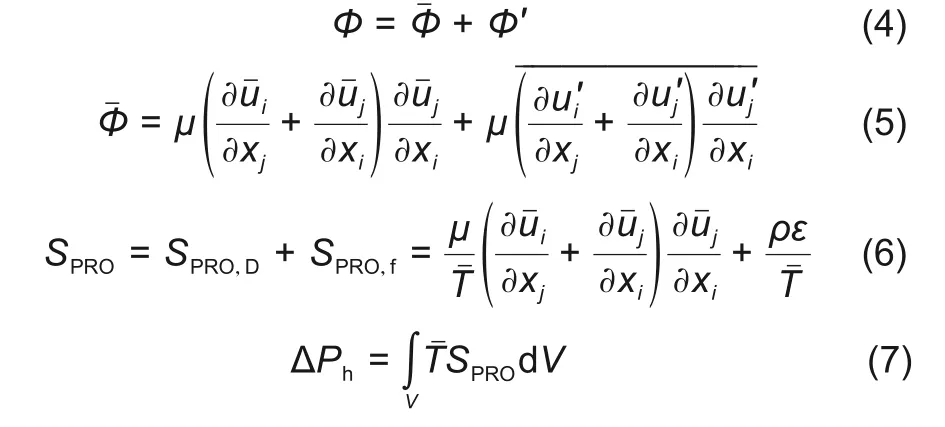
机械损失可根据摩擦力做功计算

式中，τw为壁面切应力，Pa·s；vw为壁面第1层网格的流体速度，m/s。

泄漏损失的计算公式为

式中，泄漏量q由数值模拟的口环间隙处的泄漏量得到，m/s3；He为泵扬程或者透平的有效水头，m。

1.3 边界设置

本文使用Fluent商用软件对泵作透平进行定常计算，湍流模型选择k-ωSST模型，使用速度-压力耦合方式求解。旋转域使用滑移网格方法，转速设置为1450 r/min。壁面设置无滑移，不同过流部件连接设置交界面方式进行数值传递。在泵运行工况，设置速度入口和静压出口边界[9]，当前转速的额定流量Qn为6.25 m3/h，计算范围为0.6～1.3Qn，出口静压设置为244623 Pa。在透平运行工况，设置旋转反向，在入口设置速度边界，出口压力边界[27]。速度范围为1.3～2.0Qn，出口压力为105Pa。操作压力设置为0 Pa。由软件默认初始化设置得到初场，当连续性函数残差值小于10−4，并且进口平均压力监测值趋于稳定后认为计算收敛。

2 模拟验证

首先对模拟计算进行网格独立性验证，选择合适数量的网格。设计4种网格方案，以转速1450 r/min、额定流量6.25 m3/h工况下的泵扬程为参照，使用流体工程杂志推荐的Richardson的网格收敛判定方法进行验证[28]。计算过程见表2，其中4种网格模型计算的无量纲扬程分别为H＊1、H＊2、H＊3、H＊4，可以看到扬程变化逐渐趋于稳定。其余变量为计算过程中的参数，r表示网格加密倍数；P＊为表观指数；Φ21ext为外推值；e21a为近似相对误差；e21ext为外推相对误差。通过计算前3种网格的收敛检验指数GCI21fine，发现其小于2%满足要求。综合考虑计算成本与精度的要求，选择方案Ⅲ的网格，网格总数为648万左右。声波流量计精度为1.0%，转速和扭矩由扭矩仪测得，其精度为0.5%，有关实验的详细信息可见前期工作[29-30]。将模拟的扬程效率曲线与实验对比，如图5所示，最佳效率点出现在1.1Qn是因为采用放大系数法设计的转轮。在小流量工况下，模拟值小于实验值，可能的原因在于小流量工况容易发生流动分离使流场变得更加复杂从而降低模型预测的精度[31-32]。总体而言，扬程的最大偏差小于3%，效率的偏差不超过2.5%，模拟值与实验值吻合良好。尽管泵模式和透平模式工作原理不一样，但适用同样的湍流模型[15,33]，因此可以认为仅对泵模式验证对于整体计算也是有效的。

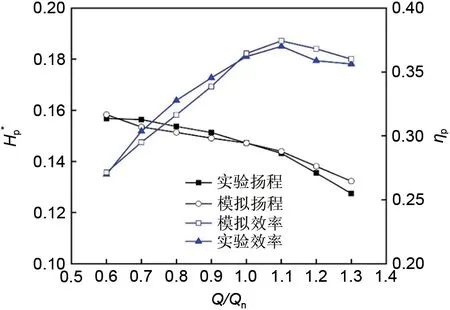
图5 实验与模拟扬程效率曲线对比Fig.5 Comparison between numerical and experimental results on head and efficiency

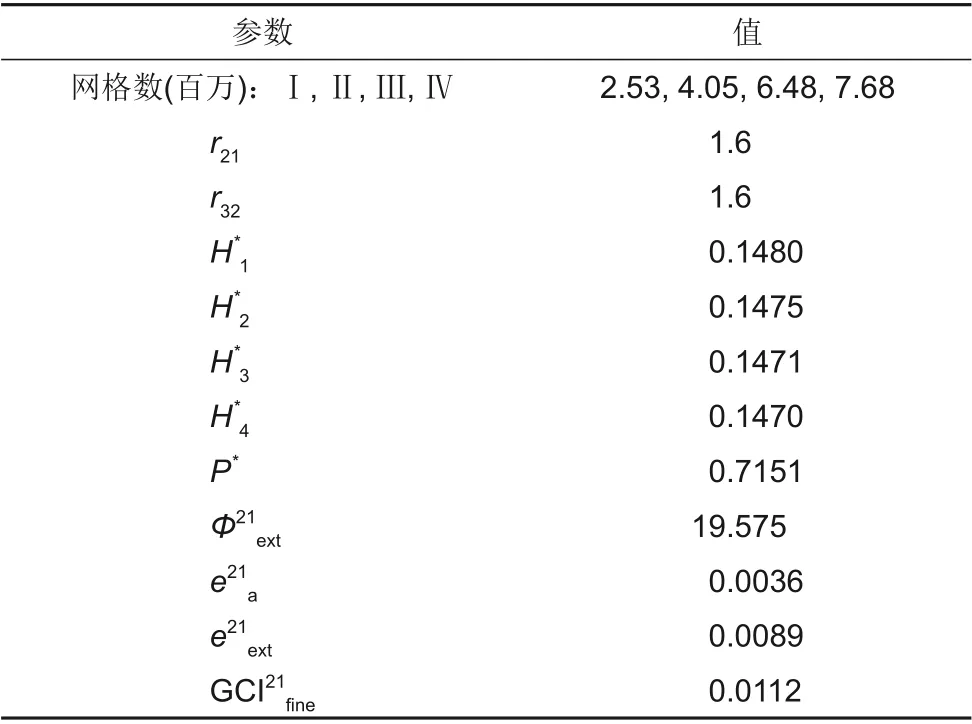
表2 Richardson网格收敛判定计算Table 2 Grid convergence method based on Richardson extrapolation

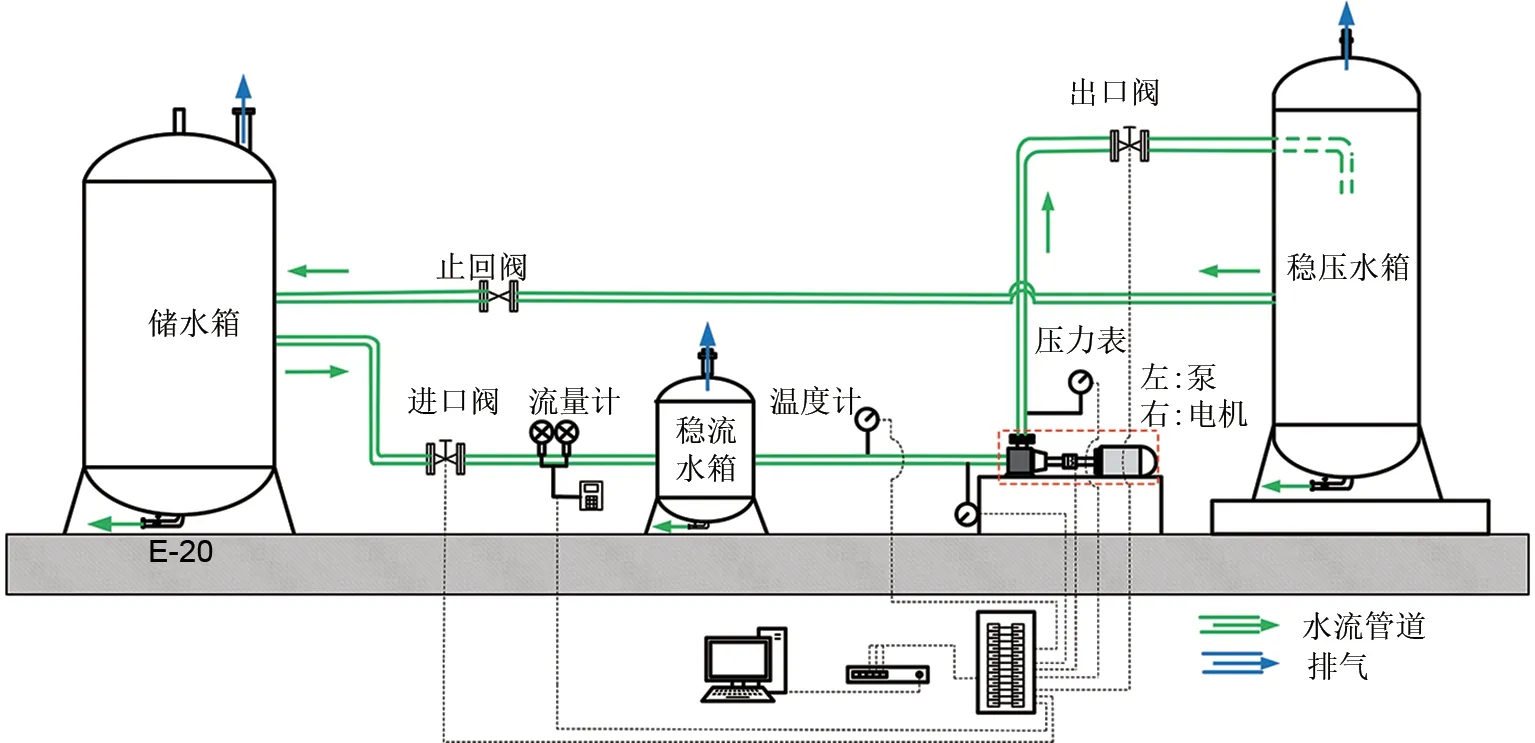
图4 实验管路Fig.4 Schematic of test loop

为了验证损失计算方法的准确性，将各损失分量计算之和与总功率损失比较，如图6所示。在泵模式中，总的损失由轴功率减去有效功率得到，此处的轴功率和有效功率由实验数据得到，损失模拟值和实验结果的偏差为1.92%。在透平模式中，总损失为总功率减去轴功率，此处功率总损失由模拟数据计算得到，两种损失计算方法偏差为3.99%。计算结果说明了损失计算的可靠性。

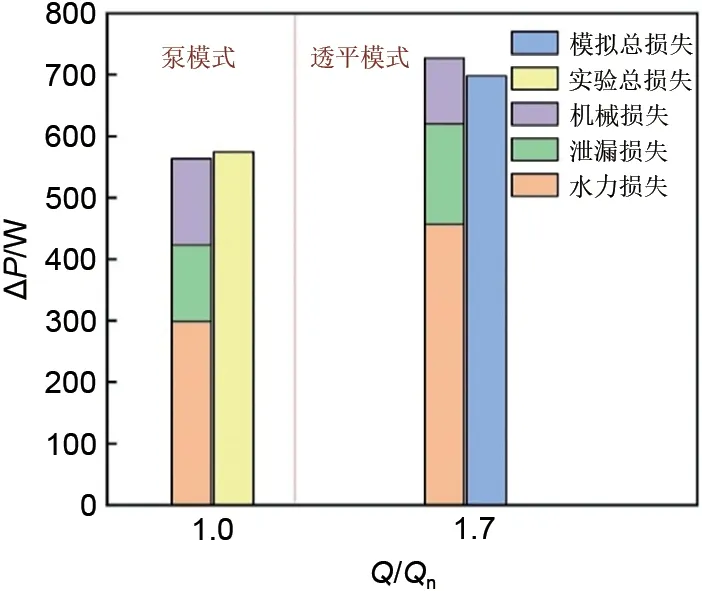
图6 损失计算方法验证Fig.6 Validation of loss calculation

3 结果与讨论

泵模式运行的扬程效率曲线如图7所示。当隔舌安放角在15°以内时，总体而言，扬程随着隔舌安放角度数增加而增加，随着流量增大，角度变化带来的影响逐渐显著。在额定流量工况，安放角为15°的扬程比角度为5°时的模拟值高6.8%，在1.3Qn工况下，前者比后者高15%左右。当隔舌安放角继续增加到20°时，扬程曲线没有明显变化，但在小流量工况下有所下降。在效率曲线中，效率随角度值增大而提高，隔舌安放角度为15°时的全局效率最优，在额定流量下，安放角为15°的效率比角度为5°时的模拟值高5.7%。但当角度增加到20°时，效率在额定流量和大流量情况下出现较大幅度的下降，大流量工况下安放角的变化会带来效率10%的波动。隔舌安放角增加还会使最佳效率点右移，角度为5°和9°时的最佳效率点在1.1Qn，而增加角度数值后其最佳效率点为1.2Qn。

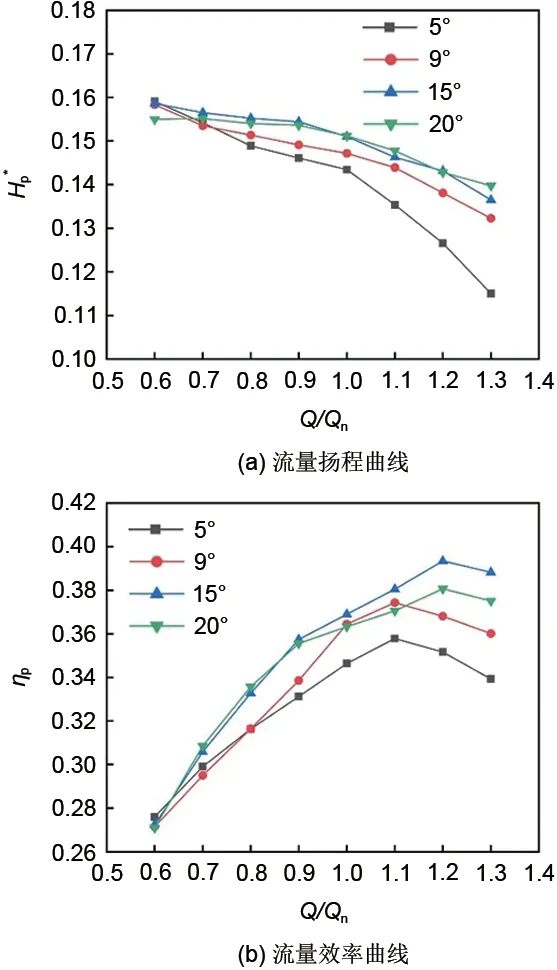
图7 泵模式下的性能曲线Fig.7 Performance curves in pump mode

透平模式的性能曲线如图8所示，透平最佳效率点流量比泵模式高30%，随着安放角增加，透平必需水头减小，最佳效率增大，在2.0Qn流量下，隔舌安放角从5°到20°，必需水头变化幅度可达30%，效率增加13%。隔舌安放角的变化同样会改变透平模式的最佳效率点位置，当角度为5°和9°时，最佳效率点在1.7Qn。角度增加到20°时，最佳效率点流量为1.9Qn。本文中由于角度取值点数的限制，没有发现效率变化拐点对应的角度值，考虑到继续增大角度会使泵性能下降，影响整体水力性能，因此不再分析更大的角度对透平水力性能的影响。

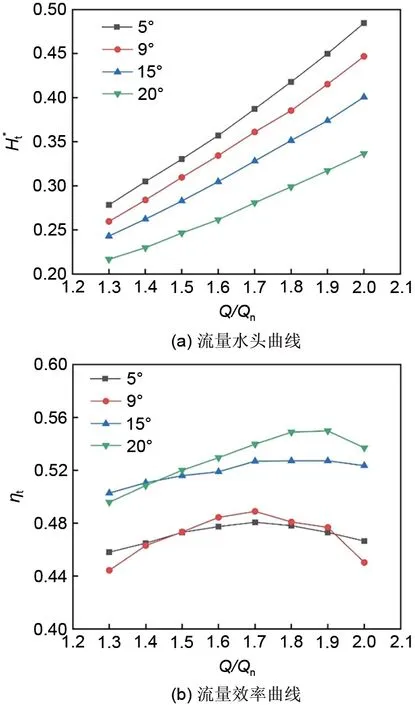
图8 透平模式下的性能曲线Fig.8 Performance curves in turbine mode

为了进一步展示相同流量工况下扬程效率随隔舌安放角的变化情况，提取泵模式下最佳效率点附近工况0.8Qn、1.0Qn和1.2Qn，以及透平模式下1.5Qn、1.7Qn和1.9Qn工况的性能参数值，变化曲线如图9所示。可以看到，与透平必需水头变化相比，泵扬程变化受隔舌安放角变化影响不明显。随着角度增加，透平模式的效率增加，而泵模式的效率变化还与流量工况有关，当角度超过泵设计隔舌角度推荐值时，在小流量下的效率会有一定的增加。

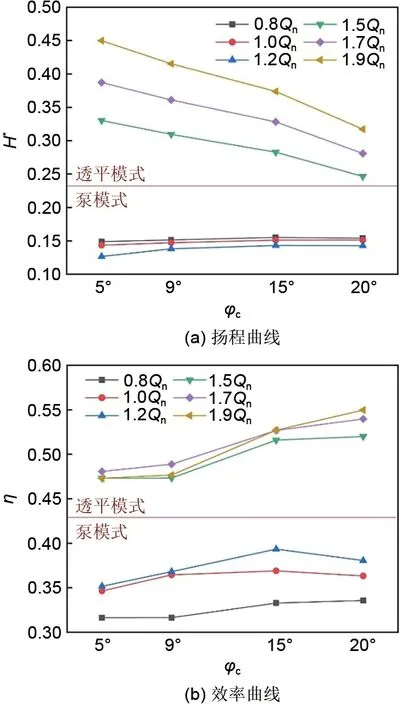
图9 扬程效率随隔舌安放角变化曲线Fig.9 Change of head and efficiency with variance of volute tongue angle

为了分析不同隔舌安放角度带来效率变化的原因，以下从功率损失的角度对其进行分析。考虑到转轮和蜗壳是最主要的过流部件，这里仅展示主要流动区域的内流损失情况，如图10所示。可以看到水力损失主要集中在蜗壳区域，并且随着角度变化，转轮内的水力损失变化不大，而蜗壳内的功率变化显著。在透平模式中，所有流量工况下水力损失的最小值都出现在隔舌安放角为20°时的模型算例中，说明此时的效率是最高的，结论与前文一致。而在泵模式中，可以根据损失最小值快速判断出1.0Qn和1.2Qn工况下的最优隔舌安放角度值，但在0.8Qn流量工况下最优角度不明显。根据泵模式和透平模式的能量损失综合判断，隔舌安放角为5°时水力损失最大，因此，两种模式运行时都应该避免选用隔舌安放角较小的低比转速泵。

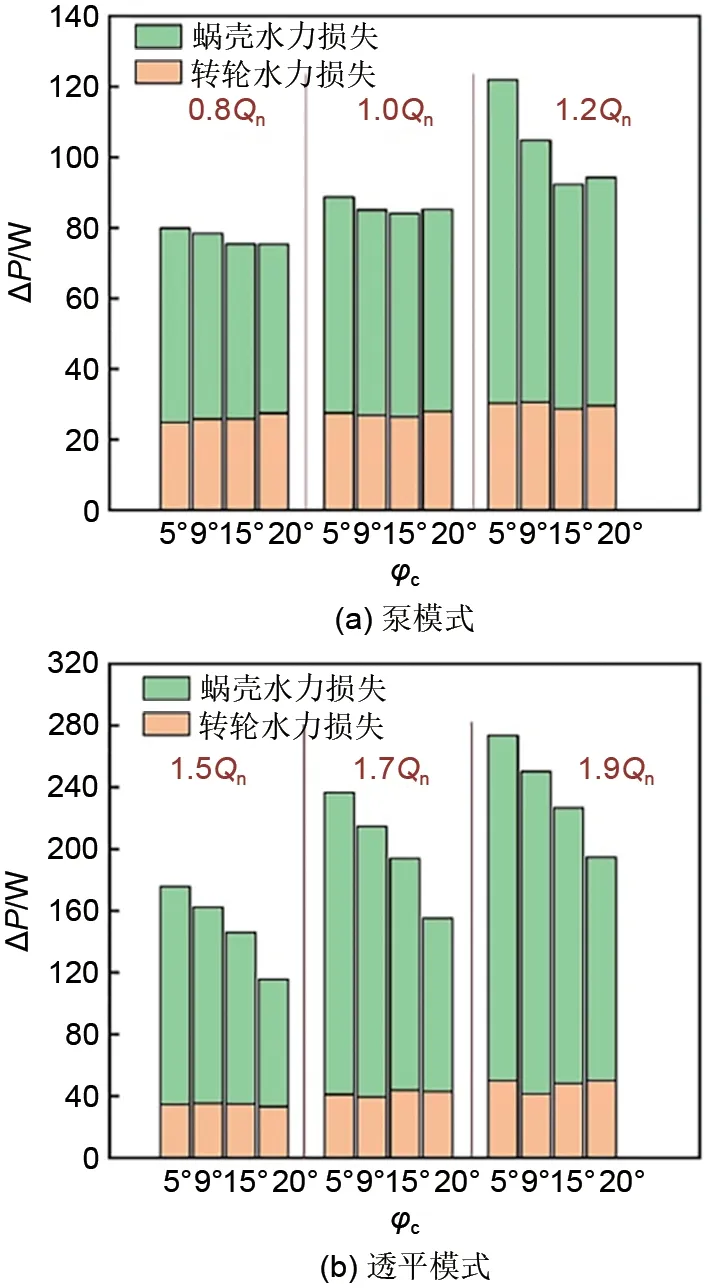
图10 不同隔舌安放角的水力损失变化Fig.10 Change of hydraulic loss with variance of volute tongue angle

使用熵产方法的优势在于可以得到水力损失的分布情况，分析流动能量耗散的极值区域，诊断不良流动区间。针对上文选取的流量工况，使用熵产率云图的方式分析隔舌安放角位置变化对流动损失耗散的影响规律。图11为0.8Qn工况时泵模式的转轮与蜗壳截面的流线与能量耗散分布情况，此时转轮内部没有明显的流动分离现象，并且损失的极值区域集中在转轮进口、转轮出口尾迹区域、转轮与隔舌间隙以及出口管区域。随着隔舌安放角度增加，在蜗壳出口处耗散逐渐减小，但在转轮与隔舌间隙区域的熵产率有较为明显的增加。在1.0Qn流量中，如图12所示，随着隔舌安放角的增加，转轮与隔舌间隙区域和蜗壳出口区域的耗散逐渐减小。图13是泵模式大流量工况下的熵产率分布，转轮内水力损失与其他流量工况相比没有明显变化，但蜗壳出口区域的耗散有显著提高，同样随着角度增加，转轮与隔舌处间隙以及隔舌出口区域的耗散减小，但角度增加超过一定范围后损失又会增大。通过以上分析，说明了在泵模式适当增大隔舌安放角，可以使蜗壳出口的能量耗散减小，泵效率增加。

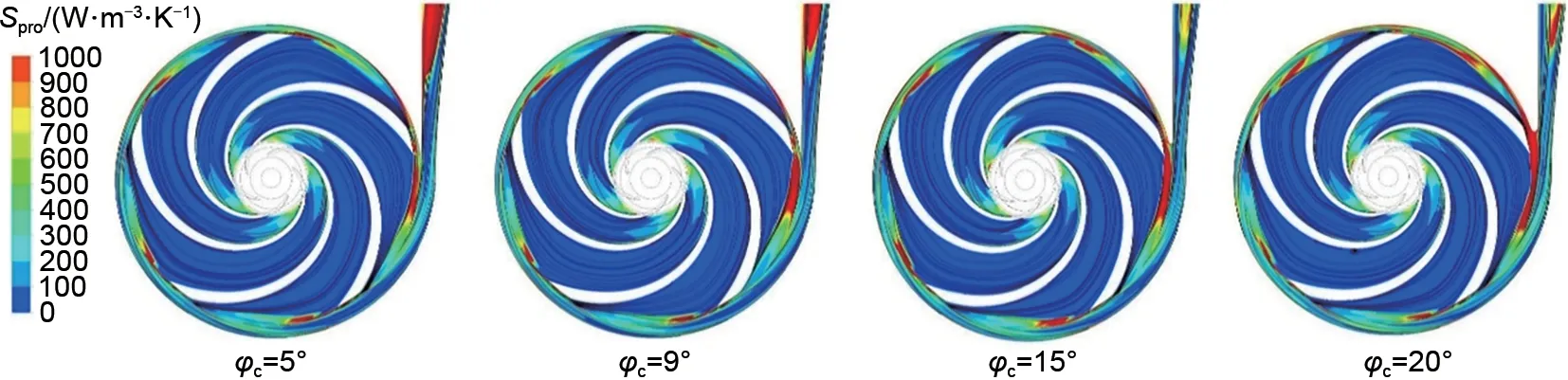
图11 泵模式0.8Qn流量工况下流线与熵产率分布Fig.11 Distribution of streamline and entropy production rate at 0.8Qn in pump mode

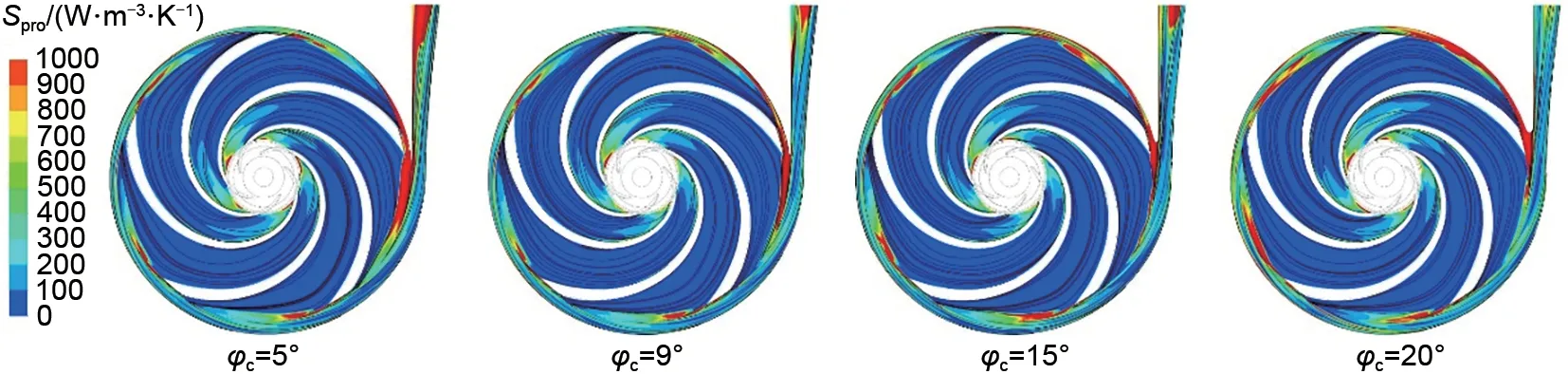
图12 泵模式1.0Qn流量工况下流线与熵产率分布Fig.12 Distribution of streamline and entropy production rate at 1.0Qn in pump mode

图13 泵模式1.2Qn流量工况下流线与熵产率分布Fig.13 Distribution of streamline and entropy production rate at 1.2Qn in pump mode

透平模式下小流量工况的熵产与流线分布如图14所示，与泵模式相比，透平模式的蜗壳进口管区域与转轮出口区域没有显著的能量损失情况，损失极值主要出现在转轮进口区域、转轮与隔舌间隙以及蜗壳壁面附近区域。转轮进口区域存在明显的流动分离现象，将损失分布与分离涡位置进行比较，发现耗散集中的区域往往不在分离涡中心，原因在于能量耗散主要与剪切效应有关，而涡中心不一定是剪切作用强的位置[26]。随着流量增加，在图15中，转轮内的流动分离现象更加显著，分离涡结构从转轮进口逐渐向下游延伸，但转轮内部的水力损失与小流量工况相比没有明显变化，主要损失区域仍在蜗壳与转轮进口区域。图16显示出转轮内流动分离在大流量情况下进一步加剧，随着隔舌安放角的增加，转轮内的分离现象受到抑制，但从熵产云图上无法得出能量耗散随之减小的规律。根据图14～16分析可以看出，尽管隔舌安放角变化影响着转轮内涡结构的分布，但转轮内的水力损失却没有明显变化，再次说明引起透平效率变化的主要原因在于蜗壳内水力损失的变化而不是转轮内的损失变化。

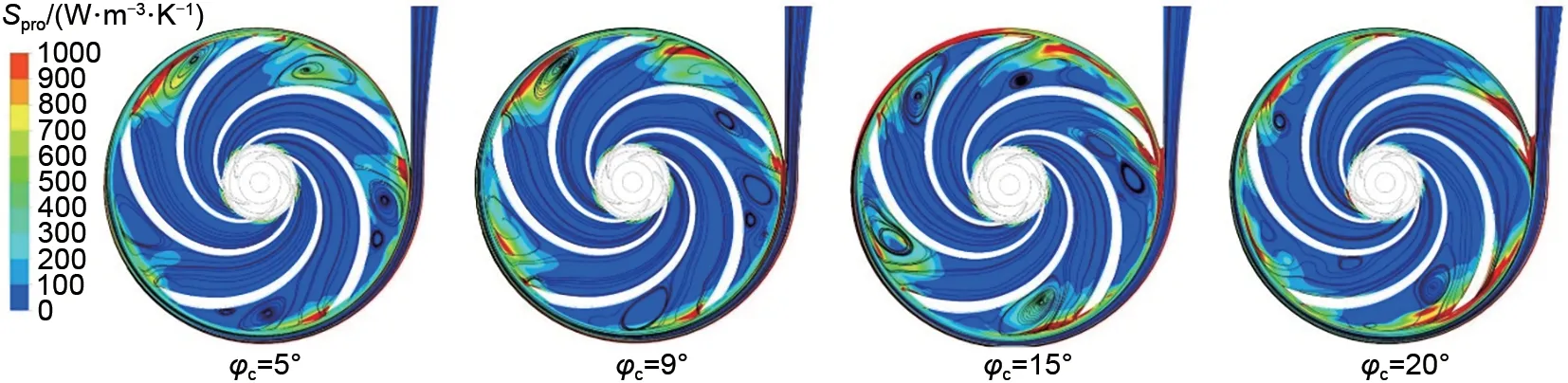
图14 透平模式1.5Qn流量工况下流线与熵产率分布Fig.14 Distribution of streamline and entropy production rate at 1.5Qn in turbine mode

图15 透平模式1.7Qn流量工况下流线与熵产率分布Fig.15 Distribution of streamline and entropy production rate at 1.7Qn in turbine mode

图16 透平模式1.9Qn流量工况下流线与熵产率分布Fig.16 Distribution of streamline and entropy production rate at 1.9Qn in turbine mode

考虑到蜗壳壁面附近有剧烈的能量耗散，较小的熵产云图阈值无法清晰展示蜗壳内部的损失变化情况，因此需要增加熵产率的云图范围并过滤掉转轮内部的损失变化情况。图17为透平模式1.7Qn工况的熵产率分布，其中S1～S4为转轮旋转方向的4个蜗壳断面，lS2和lS4分别位于对应断面的中间位置。图中发现即使转轮内部有着强烈的分离涡现象，其水力损失也远小于蜗壳与转轮间隙以及蜗壳壁面附近区域的损失。随着隔舌安放角度的增大，间隙处的损失逐渐减小，对比角度为5°和20°情况下的壁面附近高损失区域范围，可以看到面积有着较为明显的减小。提取lS2和lS4线上的熵产率曲线如图18所示，其中Z为轴向距离，图中显示壁面上存在极高的熵产率，并且其值沿壁面法向迅速下降，在远离壁面位置的损失几乎可以忽略不计。S4断面的熵产率曲线与S2断面的曲线分布有相同的变化规律，但S4断面的损失更小。随着隔舌安放角增加，壁面附近的耗散逐渐降低，当角度从5°增加到20°时，损失几乎减小了一半。通过以上分析说明，在透平运行工况中，虽然增加隔舌安放角可以抑制转轮内的流动分离，但分离涡不是影响效率的主要因素，蜗壳与转轮间隙以及蜗壳壁面附近的损失减小才是效率增加的主要原因。

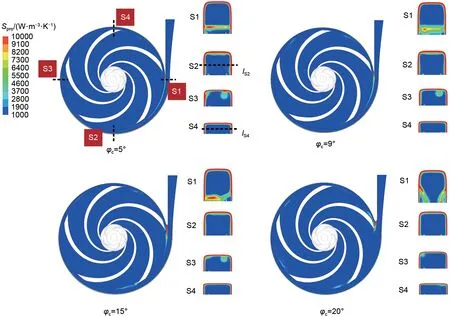
图17 透平模式1.7Qn流量工况下熵产率分布Fig.17 Distribution of entropy production rate at 1.7Qn in turbine mode

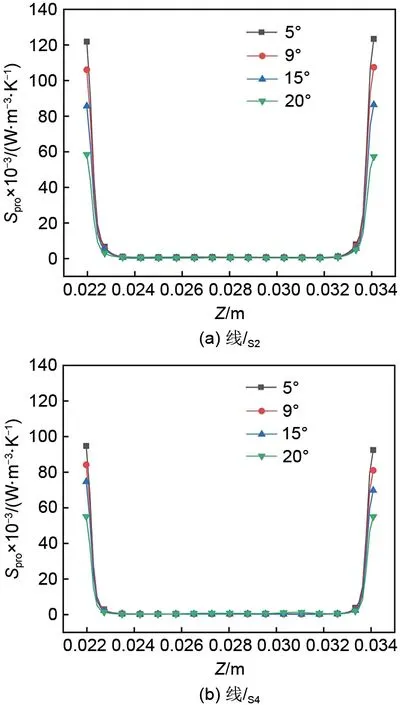
图18 透平模式1.7Qn流量工况下不同监测线上的熵产率分布Fig.18 Entropy production rate change on different monitor lines at 1.7Qn under turbine mode

4 结 论

本文以一低比转速离心泵为研究对象，讨论了不同隔舌安放角对泵作透平正反模式运行水力性能的影响，以数值模拟为主要研究手段，结合熵产诊断方法，分析了泵扬程、透平必需水头、效率以及能量损失的变化规律，得到以下结论。

（1）在泵模式中，一定范围内增加隔舌安放角时，可以提高扬程和效率，并且在大流量下效果更显著。隔舌安放角从5°增加到15°时，额定工况下的扬程增加6.8%左右，效率增加5.7%。当隔舌安放角度增加超过15°时，扬程没有明显变化，效率在设计流量和大流量时降低。效率曲线中最佳效率点位置随该角度增加出现右移，其对应的流量值增大。

（2）在透平模式中，增加隔舌安放角使必需水头减小，效率增加。当角度从5°增加到20°，大流量工况的必需水头可减少30%左右，效率增加13%。同样隔舌安放角度的增加会使效率-流量曲线右移。

（3）两种模式下的水力损失都集中在蜗壳区域，与转轮内损失相比，其受隔舌安放角角度变化影响更为显著。在泵模式，水力损失极值出现在转轮进口、转轮尾迹、转轮与隔舌间隙以及蜗壳出口区域。当隔舌安放角在一定范围内增加，蜗壳出口区域的水力损失减小，泵效率提高。在透平模式，水力损失极值出现在转轮进口区域、转轮与隔舌间隙以及蜗壳壁面附近区域。增加隔舌安放角可以抑制转轮内流动分离，但分离涡结构变化不是影响透平效率的主要因素，蜗壳与转轮间隙以及蜗壳壁面附近的损失减小是效率增加的主要原因。