一种可信任的大容量无载体信息隐藏方案

杜耀刚 杨自力 张艳硕 王泽豪

1(北京电子科技学院 北京 100070)

2(西安电子科技大学通信工程学院 陕西 西安 710071)

3(数据通信科学技术研究所 北京 100191)

0 引 言

信息隐藏技术[1-3]分为嵌入式信息隐藏技术[4-5]和无载体信息隐藏技术[6-8]。无载体信息隐藏技术的研究领域主要有基于文本[9-10]和基于图像两个方向。目前在图像方面进行的无载体信息隐藏方案，大多数集中在如何利用图像的特征变化规律来进行信息的隐藏设计。如将图像进行3×3分块，然后通过每块像素值按一定规则进行比较产生秘密比特信息[11]；又或者将图像分块之后通过比较子块像素值变化方向来产生秘密比特信息[12]。这其中存在许多问题，如信息隐藏图像在传输过程中受到攻击或者刻意篡改，那么接收方就会提取出错误的秘密信息。同时这些方案每幅图像只能与固定的隐秘信息进行对应，如果要传输大量秘密信息则需要大量的图像，这就将产生不小的存储负担。而且这些方案的隐藏容量相对较低，还有很大的提升空间。

针对以上问题，本文提出了一种既能验证图像完整性，同时减少系统存储资源消耗并且有很高隐藏容量的无载体信息隐藏方案。该方案是基于线性码[13]的生成矩阵和校验矩阵思想结合混沌映射理论以及迭代线性方程组[14]设计的无载体信息隐藏系统。方案通过提取图像的像素值，然后经过设计的系统的一系列变换来确定图像与密文信息的对应规则。信息发送方和接收方分别通过无载体信息隐藏系统可确定需要发送的图像信息和接收的密文信息。该方案创新性地将混沌加密算法嵌入到线性码理论中形成一种新的信息隐藏算法，使得信息在隐藏过程中具有混沌加密算法的随机性和安全性，同时具有线性码的可验证性。另外与图像对应的秘密信息在算法的实现过程中形成了相比于其他算法容量大的特点，并且由于两者之间的动态关联性，大大减少了信息库的存储资源消耗。

1 线性码原理

图像在传递的过程中可能会遭受到攻击方刻意的篡改或者数据缺失，这样就会导致接收方解密出错误的信息。为了避免出现这种情况，方案利用线性码的可验证性对信息进行认证。

现有一个有限域Fq，若q=pn，其中p为素数。则称其n维向量空间为Qn，也记作Rn。

定义1若C是一个[n,k]线性码，则C也一定是有限域Fq上的n维线性空间Rn中的一个k维线性子空间。

定义2一个k×n矩阵G,其行向量构成的基底若能经过线性组合表示[n,k]线性码C中的任何码字即：

C={aG|a∈Qk}

则称矩阵G为线性码C的生成矩阵。若G=(Ik,P)是标准型的矩阵,即Ik是k×k的单位矩阵,则每个码字的前k个符号用来表示信息位,后面的n-k个符号用来表示校验位。

定义3若C是一个[n,k]线性码,那么其对偶码C⊥为:

2 混沌映射理论

混沌系统是指在一个确定性系统中，存在随机的不规则的运动，其行为表现为不确定性、不可重复性、不可预测性，这就是混沌现象。针对这种现象产生了多种混沌映射系统：一维Logistic映射、二维Henon映射、三维Lorenz映射等。本文采用的是一维Logistic混沌映射[15]对信息进行加密。

Logistic混沌映射从数学形式上看是一种相对简单的混沌系统，但却具有极其复杂的动力学行为，在选定合适的初始条件下，产生的混沌序列是非周期的、不收敛的、无法预测的。其数学表达式如下：

xk+1=μxk(1-xk)

(1)

式中：μ为系统参数，根据输出需求可以确定对应的k值，0<μ≤4，xk∈(0，1)。如果初始参数发生变化，那么对应的混沌序列也会跟着发生变化，且这种变化是无规律的。因此，确保了加密系统的安全性。本文方案初始参数x0取值为0.5，通信双方通过协商之后在3.57≤μ≤4之间选取一样的μ值来输出混沌序列。

3 无载体信息隐藏简介

无载体信息隐藏的提出是针对传统的嵌入式信息隐藏难以抵抗发展迅速的各类隐写分析算法[16-18]的检测。而难以抵抗检测的根本原因是嵌入式的信息隐藏方式改变了载体信息，虽然嵌入方式是采用载体信息的冗余度进行的，可以让人无法通过感官系统察觉出来，但是却逃不过隐写分析算法的检测。

无载体信息隐藏技术依然需要载体进行信息的传输，与以往的信息隐藏方式不同的是，它没有改变载体信息，而是利用载体本身具有的特征按照一定的规则来构成与秘密信息的对应联系，以此来达到传输秘密信息的目的。当然，为了增加安全性会对特征信息进行量化加密处理。无载体信息隐藏技术利用的传输载体是原始的、未作改变的，因此不会引起攻击者的怀疑，也不会被各类隐写分析算法检测出来。由于具有出众的保密通信优势，这项技术受到了大量专家的重视。

4 无载体信息隐藏方案

本节给出了所提的具体无载体信息隐藏实现方案，该方案是通过对选取的图像进行像素值的处理，得到对应的像素矩阵，然后对像素值的二进制矩阵利用线性码的校验原理作可验证运算，之后对生成的矩阵信息与经过混沌加密的参数矩阵一起构建迭代线性方程组，然后利用经过迭代线性方程组变换得到的矩阵信息与公开的矩阵信息一起得到最终传输的隐秘信息，最后利用坐标信息即可在信息库中找到相应的密文信息。发送方通过以上方案的步骤得到密文信息与图像的对应关系，然后根据要传输的密文信息找到对应的图像进行发送，接收方接收到图像之后，根据方案的步骤进行处理就可得到对应的隐秘矩阵信息，进而得到密文信息，并可对信息的完整性进行验证。方案的具体步骤先后分为图像处理、参数生成与发送、信息提取和完整性验证四部分。

4.1 图像处理

一幅灰度图像，可由r0×s0个像素pij(1≤i≤r0,1≤j≤s0)所构成，因此可以将图像用一个矩阵M来表示, 其中pij为图像的组成像素值。

设有m幅传输图像，其对应的像素矩阵为r0×s0的矩阵Mi(i=1,2,…,m)。本文的任务即将这m个传输图像提取像素值通过矩阵生成算法用m个矩阵来表示。

4.2 参数生成与发送

步骤1按照线性码理论随机生成一个s0×n0的标准型生成矩阵G(Gij∈[0,1])，对矩阵Mi(i=1,2,…,m)，按式(2)计算对应的Si(i=1,2,…,m)。

Si=MiGi=1,2,…,m

(2)

此时根据生成矩阵G的校验位矩阵提取出对应在Si(i=1,2,…,m)上的验证矩阵Ji(i=1,2,…,m)，根据定义2可知验证矩阵Ji(i=1,2,…,m)为Si(i=1,2,…,m)的后面n-k列形成的矩阵。

Mi来自于图像的像素值作模二运算生成的二进制矩阵，本方案选用的生成矩阵G是标准型的矩阵，能最后对图像的完整性进行有效的检验。

步骤2根据需求设置n个初始未经加密的参数矩阵Bi(i=1,2,…,n)和选定初始值μ之后由式(1)产生混沌序列进而转化的混沌矩阵L，对参数矩阵Bi(i=1,2,…,n)按式(3)得到加密参数矩阵Ci(i=1,2,…,n)。

Ci=Bi⊕Li=1,2，…，n

(3)

定义如下矩阵序列：

S1,S2，…，Sm,C1,C2，…，Cn,D0,D1，…，Dn+m

其中，Di(i=0,1,…,n+m)是通过在它之前的n+m个矩阵进行运算而得到。即：

(4)

步骤3根据需要设置矩阵Ti(i=1,2,…,N)，其中1≤N≤m+n，然后计算Ki(i=1,2,…,N)：

Ki=Di-Tii=1，2，…，N

(5)

合并Ki(i=1,2,…,N)得到映射矩阵Yi(i=1,2,…,N)，找出密文信息在映射矩阵上对应的坐标信息Zi(i=1,2,…,N)，即可实现无载体信息隐藏。

步骤4将信息G,Bi(i=1,2,…,n),Ji(i=1,2,…,m),Ti(i=1,2,…,N),Zi(i=1,2,…,N)公开。混沌加密系数μ通过可靠信道传送给接收方。

4.3 信息提取

秘密接收方接收到图像之后对图像进行解析生成矩阵Mi(i=1,2,…,m)，由式(2)和公开的生成矩阵G，可计算得Si(i=1,2,…,m)。再由得到的混沌加密系数μ得到混沌矩阵L，由公开的Bi(i=1,2,…,n)按式(3)得到加密参数矩阵Ci(i=1,2,…,n)，结合式(4),可将S1,S2，…，Sm,C1,C2，…，Cn转化为：

(D0,D1,…，Dn+m)T=Q(S1,S2，…，Sm,C1,C2，…，Cn)T

(6)

式中：系数a通过式(4)合并同类项得到。此刻也就能解出Di(i=0,1,…,n+m)。最后通过公开的矩阵Ti(i=1,2,…,N)，结合式(5)，可计算出秘密矩阵Ki(i=1,2,…,N)，之后变换得到映射矩阵Yi(i=1,2,…,N)，由坐标信息Zi(i=1,2,…,N)即可找到在信息库中对应的密文信息。

4.4 完整性验证

5 方案实现

本文选取的三幅实验图像——lena、baboon、airplane均为512×512灰度图像，如图1所示。

图1 实验用图

5.1 发送方

将lena、baboon、airplane三幅实验用图的像素调整为8×8之后，其像素矩阵分别如图2所示。

图2 lena,baboon,airplane像素矩阵(8×8)

对以上像素矩阵值模2取余生成二进制矩阵Mi(i=1,2,3)分别如图3所示。

图3 lena,baboon,airplane二进制矩阵(8×8)

然后构造一个标准型生成矩阵G(8×9)，如图4所示。

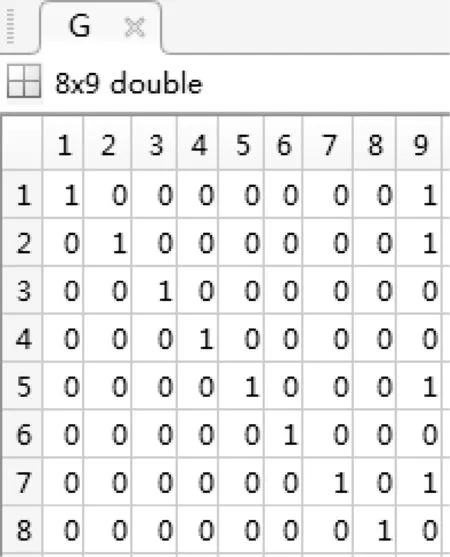
图4 生成矩阵G(8×9)

由式(2)可得Si(i=1,2,3)如图5所示。

图5 矩阵Si(i=1,2,3)(8×9)

由于传送的图像为3幅，因此，设置矩阵Bi(i=1,2)，如图6所示。

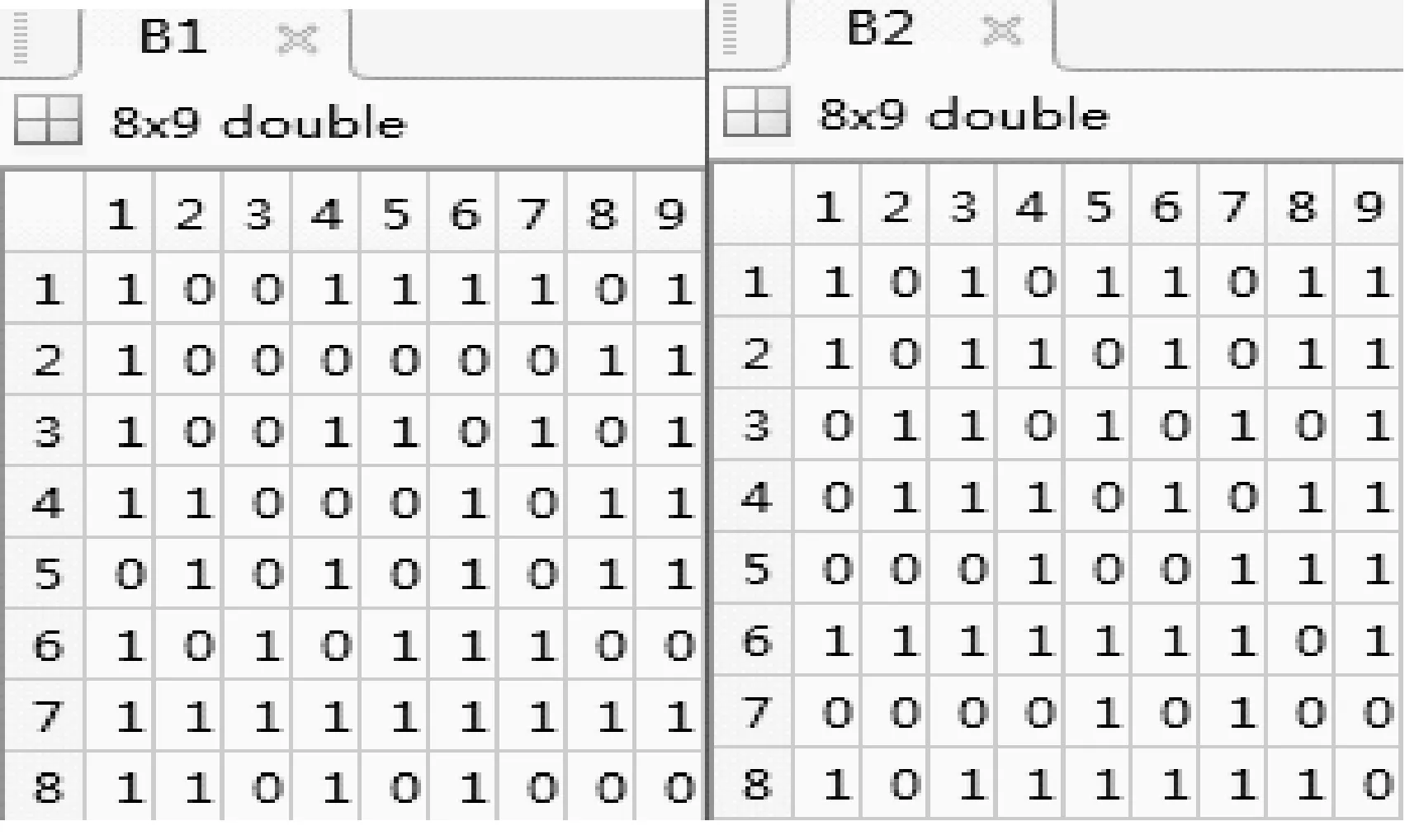
图6 矩阵B1,B2(8×9)

根据传输的μ值取3.8和式(1)可得到对应的混沌序列转化的混沌矩阵L如图7所示。

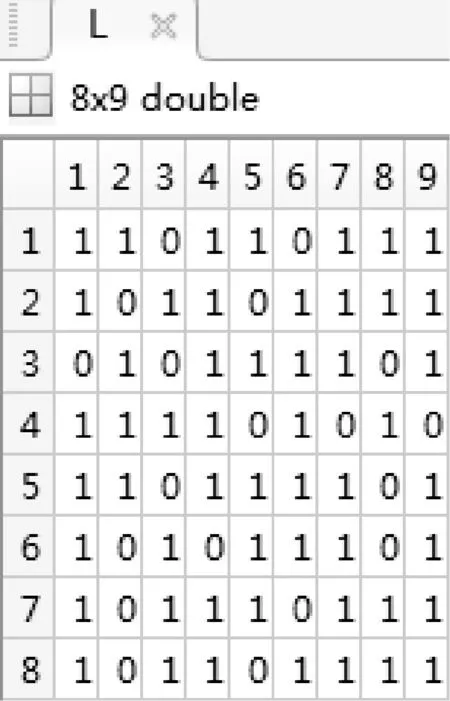
图7 矩阵L(8×9)

根据Bi(i=1,2)，混沌矩阵L和式(3)，可求得参数矩阵Ci(i=1,2)如图8所示。

图8 矩阵C1,C2(8×9)

根据Si(i=1,2,3)、Ci(i=1,2)和式(4),可求得Di(i=0,1,…,5)如图9所示。

图9 矩阵Di(i=0,1,…,5)(8×9)

设置生成两个8×9矩阵T1、T2如图10所示。

图10 矩阵T1,T2(8×9)

由式(5)可得K1、K2如图11所示。

图11 矩阵K1,K2(8×9)

将矩阵K1、K2每三位信息合并生成映射矩阵信息Y1、Y2如图12所示。

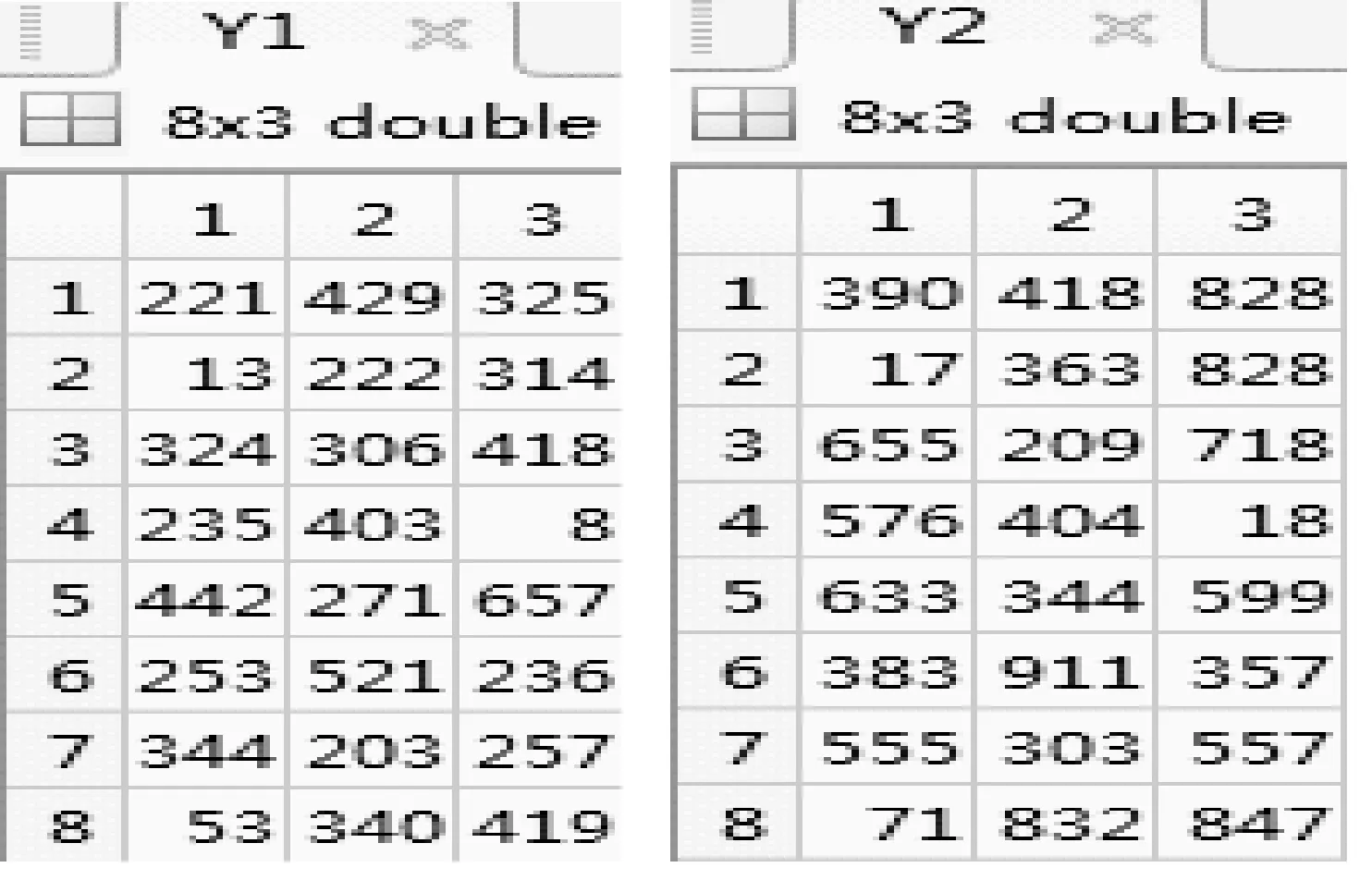
图12 矩阵Y1,Y2(8×3)

若传输的信息为“北京”，而信息库的对应关系为“北”↔“013”，“,京”↔“018”，则找到在矩阵中对应的坐标信息Z1=(2,1),Z2=(4,3)，至此，公开G、T1、T2、B1、B2、Z1、Z2,然后将图像发送给信息接收方，混沌系数μ通过可靠信道传输，信息发送的步骤完成。

5.2 接收方

秘密接收方接收到图像之后对图像进行解析生成矩阵Mi(i=1,2,…,m),由式(2)和公开的生成矩阵G，可计算得Si(i=1,2,…,m)。再由接收到的混沌加密系数μ通过混沌映射变换由公开的Bi(i=1,2,…,m)也就能计算得到Ci(i=1,2,…,n)，结合式(4),这时本文可以解出Di(i=0,1,…,n+m)。最后通过公开的Ti(i=1,2,…,N)，结合式(5)，可计算出加密矩阵Ki(i=1,2,…,N),然后可对应得到映射矩阵Yi(i=1,2,…,N),根据得到的坐标信息Zi(i=1,2,…,N)，参照信息库即可得到传输的密文信息如图13所示。

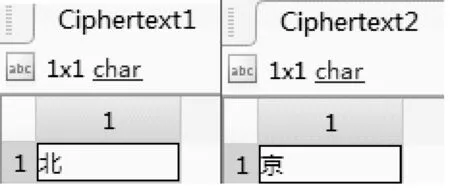
图13 密文信息

信息完整性验证，由于生成矩阵G为标准型矩阵G=(Ik,P)，因此在本方案中其校验矩阵为：

H1=[11001010]

图14 Mi(i=1,2,3)校验结果正确

假设由于传输过程中图像遭到信息的篡改或破坏，进而导致Mi(i=1,2,3) 中一个或多个出现变动，例如图像lena信息被篡改导致M1中出现错误，如图15所示。

图15 M1黑框中数据出现错误

那么，J1+M1HTmod 2后得到的校验结果就不再是0，可以判断接收数据出现错误，如图16所示。

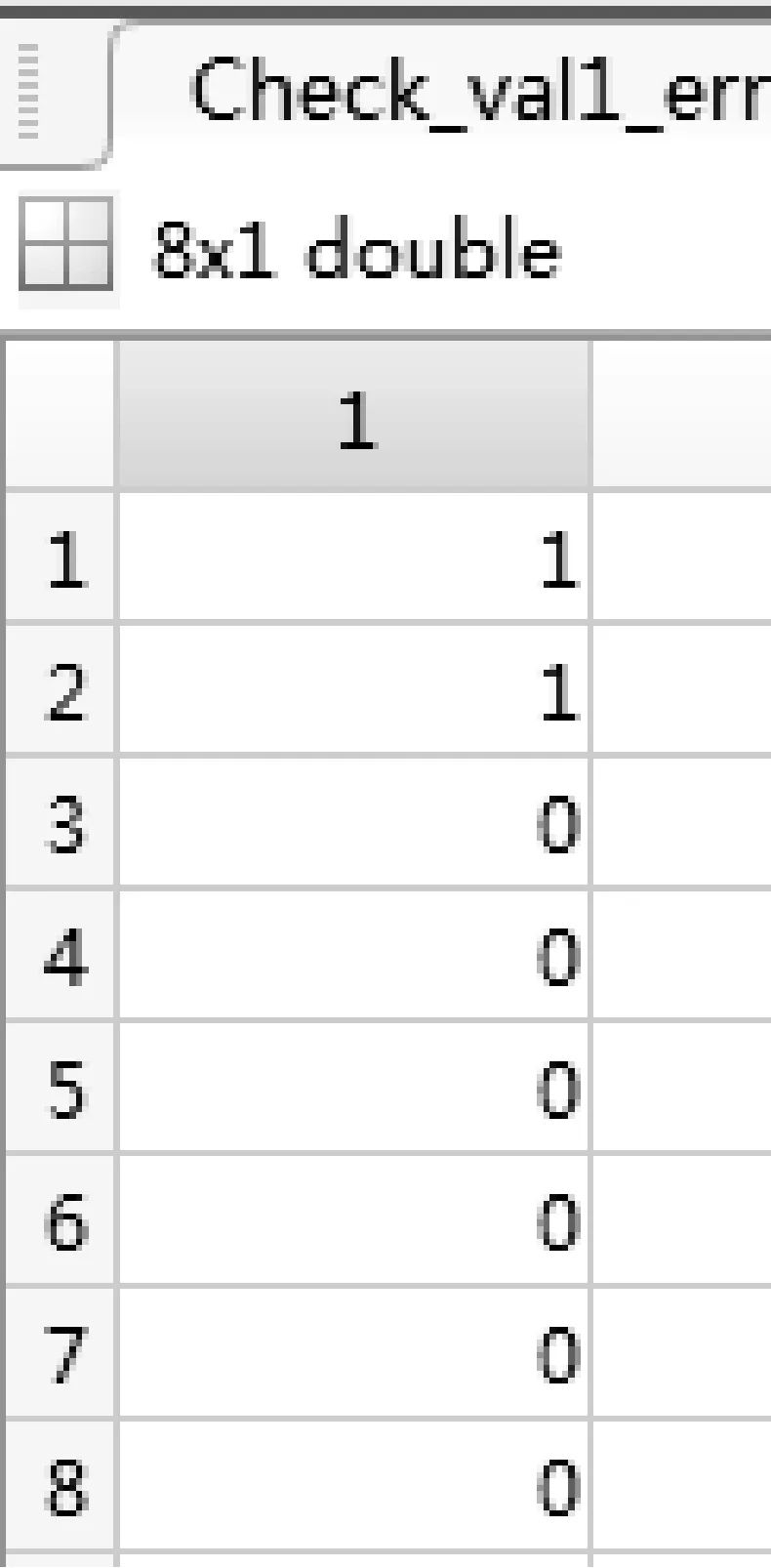
图16 错误的M1导致错误的校验值

6 方案特性分析

6.1 隐藏容量分析

该方案是通过对3幅图像进行像素值处理，得到对应的3个像素矩阵，然后对像素矩阵利用线性码的校验原理作可验证处理。之后对生成的矩阵信息与经过混沌加密的参数矩阵一起构建迭代线性方程组，利用迭代线性方程组得到的矩阵信息与公开的矩阵信息一起获得最终要传输的隐秘矩阵信息，然后根据矩阵的坐标信息找到与信息库对应的密文信息。方案采用的是利用3幅图像进行传输，最终解密出2个秘密信息矩阵的形式进行信息的传输。另外本方案的图像分割方式是采用8×8的像素值矩阵进行，为了便于与其他方案进行对比，本文采用3×3的形式进行计算。故解密出的信息矩阵形式是3×4，由于十进制信息矩阵每个值代表3比特的二进制信息，因此平均每幅图片最后可表示的比特值信息是:

3×4×3×2÷3=24 bit

与其他方案对比信息如表1所示。

表1 隐藏容量对比

由表1对比可知，本文方案相比于其他两种方案在隐藏容量上有了较大的提高，隐藏容量是文献[11]方案的四倍，比文献[12]方案隐藏容量提升三分之一。

6.2 可验证性分析

为了防止秘密信息在传递过程中遭遇毁坏或篡改而导致接收方无法察觉进而解密出错误信息，本文设计了一个可信任的无载体信息隐藏方案，需要根据线性码理论中的生成码和校验码的思想，在解密信息的过程中加入生成矩阵和校验矩阵进行完整性的验证，验证步骤如下：

步骤1通过信息发送方公开的生成矩阵G，根据定义3可得到对应的校验矩阵H1。

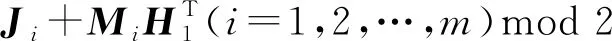
表2 可验证性对比

6.3 安全性分析

该方案在信息的加解密的过程中引入了迭代线性方程组的形式使得信息被解密的难度加大，同时将混沌映射加密系统嵌入到加解密过程中，使得系统具有了混沌映射的随机性、混沌特性,攻击方无法找出其中的输入输出关系，若攻击方无法得到正确的混沌加密系数，则根本进行不了解密操作，故本文方案具有很强的安全性。

6.4 存储资源消耗分析

本文方案由于将图像的像素值矩阵作为加解密信息的一环，与设置的混沌加密矩阵Ci(i=1,2,…,n)一起导出最终的秘密信息矩阵。同一幅图像，与不同的参数矩阵Ci(i=1,2,…,n)将对应的是不同的秘密信息矩阵，故图像与秘密信息矩阵是动态关联的。一幅图像将可以表示大量的隐秘信息，而传统无载体信息隐藏系统，图像与隐秘信息是一对一的关系。因此本文方案能大大减少无载体信息隐藏系统的存储资源消耗。

7 结 语

本文提出了一种利用线性码的生成矩阵和校验矩阵思想结合迭代方程组以及混沌映射加密设计的无载体信息隐藏方案。该方案能在接收方收到图像信息之后对图像信息的完整性进行验证，避免提取出错误的信息。而一般的无载体信息方案则无法抵抗来自攻击方对信息的无差别攻击引起的解密误差。并且方案采用了迭代方程组以及混沌映射系统结合的方式，使得系统的安全性和随机性很高。因此这是一个可信任的无载体信息隐藏方案，同时该方案有着很大的隐藏容量提升，隐藏容量是文献[11]方案的四倍，相比文献[12]方案提升三分之一。并且方案的图像信息与密文信息是动态关联的关系，大大减少了系统的存储资源消耗。