基于门限ECDSA的定期可更新的比特币密钥管理方案
韩妍妍 徐鹏格 李兆斌 魏占祯
1(西安电子科技大学通信工程学院 陕西 西安 710071)
2(北京电子科技学院通信工程系 北京 100070)
0 引 言
比特币[1]是中本聪于2008年提出的一种点对点的电子现金系统。与传统的银行交易不同,任何规模的比特币交易都依赖于ECDSA。用户独立创建和存储一个公私钥对,其中公钥通过单向哈希函数可以导出一个比特币地址,而对应的私钥仅由用户自身可见并用于签名交易。该过程完全独立于比特币网络,且无须访问区块链或互联网。矿工利用公钥对交易的数字签名进行验证,如果验证通过则将该笔交易记录在区块链中,否则抛弃该交易。由此可见,比特币的安全性等同于授权交易的私钥的安全性。一旦私钥泄露,比特币将会被盗。即使已知货币被盗,也无法扭转违规交易。
最早的用户只能生成和存储有限个私钥,这种管理方式显然无法满足比特币用户的需求。2012年,Wuille[2]提出一种分层确定性密钥管理方案,即可由一个种子以树状结构衍生任意多个密钥,这从根本上解决了私钥不易再生和难备份的问题,该方案被记为第32项比特币改进协议(BIP-32)。2013年,Palatinus等[3]提出可用一组容易记忆的单词来生成密钥种子,这样更加易于用户从本地导入和导出比特币密钥。与用二进制或十六进制表示的种子相比,助记词与人类的交互会更优越。该提议被记为第39项比特币改进协议(BIP-39)。2014年,Bamert等[4]设计了一种低功耗的蓝牙硬件钱包,用于实现对比特币密钥的物理保护。然而传统对密钥进行单一位置存储的方法可能会导致黑客匿名地、不可逆转地盗取用户的所有资金。
对比特币进行联合控制可有效解决这一问题,攻击者若想完成欺诈性交易必须破坏超过阈值的设备。多重签名是指比特币地址需要与n个指定公私钥对相关联,花费上面的比特币至少需要t个签名。但由于多重签名会暴露团体的访问策略,导致用户的匿名性变弱,这并不是最好的比特币联合控制方案。2016年,Gennaro等[5]提出利用门限签名方案替代多重签名更加安全合理,并在Mackenzie等[6]提出的双方ECDSA方案的基础上提出了一种最优门限ECDSA方案。在n个成员中,任意t个或更多个成员可联合对某个消息进行签名。然而,以上方案需要完成分布式Paillier密钥生成,这是非常昂贵和不切实际的。Zhou等[7]提出一种分布式比特币账户管理(DBAM)框架,利用基于属性的加密算法实现企业和公司对比特币账户的细粒度管理,但该方案并未真正实现去中心化,仍然需要一个主账户完成私钥份额分发及交易签名。2018年,Lindell等[8]通过利用支持加性同态的指数型ElGamal替换Paillier加密算法来解决文献[5]方案中的问题。但是,Lindell等[8]所设计的指数型ElGamal并不是有效的加密方案,其解密过程需要解决离散对数难题,因此只有当签名消息相对较小时,该方案才能顺利执行。同年,Gennaro等[9]通过引入一种份额转换协议来改进其原始方案[5],该协议允许双方将秘密的乘法份额转换为同一秘密的加法份额。该方案中的每个玩家最终只需要在本地生成自己的Paillier密钥即可。此外,双方ECDSA[6,10-11]更符合个体用户增强比特币密钥的安全需求,Mann等[12]将电脑桌面钱包与智能手机钱包结合的方法则是双方ECDSA的应用实例。
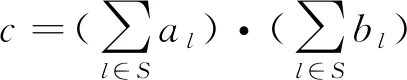
1 基础知识
1.1 椭圆曲线数字签名
椭圆曲线数字签名算法[13-14](ECDSA)由阶为p,生成元为G的循环群参数化,其中G为某条椭圆曲线上的点。ECDSA具体定义如下:
Gen(1κ):随机选择一个私钥sk∈Zq,计算公钥Q=sk·G。输出公私钥对(Q,sk)。
Sig(sk∈Zq,m∈{0,1}*):随机选取一个随机数k∈Zq,计算(rx,ry)=R=k·G。然后计算s=k-1·(H(m)+sk·rx),输出数字签名σ=(s,rxmodq)。
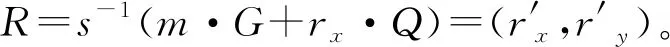
1.2 陷门承诺方案
承诺方案[15-17]允许发送者先对消息做出承诺而后再对验证者打开。陷门承诺方案一般由密钥生成(KG)、承诺(Com)、打开(Open)、验证(Ver)四个算法组成,具体如下:
KG:密钥生成算法。输入相关安全参数,该算法输出一对公私钥对(pk,tk),其中:pk是与方案相关的公钥;tk又称为陷门。
Com:承诺算法。输入公钥pk和消息M后,输出[C(M),D(M)]=Com(pk,M,r),其中r为硬币投掷。C(M)用于做事先承诺,D(M)是用于稍后揭密消息M。
Open:打开承诺算法。输入C(M)、D(M)、公钥pk后,输出消息M或者⊥。
Ver:验证算法。输入公钥pk、消息M、R,以及一个新消息M′≠M、T。如果T=tk,那么输出D′使得Ver(pk,C(M),D′)=M′。
1.3 Shamir门限方案
1) Shamir门限方案[18]:给定秘密值s∈Zq,成员个数n及阈值t(t≤n)。分发者D在Zq上选择一个t-1阶的多项式:
f(x)=a0+a1x+…+at-1xt-1modq
(1)
计算每个子秘密值xi=f(i)并秘密分发给成员,则任意t个成员即可利用拉格朗日插值公式恢复秘密值。
2) 拓展方案1(Feldman等[19]可验证秘密共享):分发者D首先广播相关值ga0,ga1,…,gat-1,然后再向成员分发秘密值。每位成员可利用式(2)验证子秘密的正确性:
gαi=(ga0)(ga1)i…(gat-1)it-1
(2)
当全部的子秘密均正确后分发阶段成功完成。
3) 拓展方案2(Baron等[20]主动秘密共享方案):分发者随机生成一个t-1阶多项式:
(3)
然后分别向成员分发秘密值f′(i),成员利用式(4)计算新的子秘密,并销毁之前的子秘密:
(4)
2 方案设计
激励模型定义如下:假设某慈善机构准备组织一场比特币全球募捐活动,并希望使用某个比特币地址来宣传此次活动。因为比特币可实现跨币种、跨国界的转账,所以该机构可以直接收到世界各地的募捐,也可以将资金快速分配给更多需要帮助的地区或个体。
由区块链的特性决定,机构的比特币交易记录是完全公开透明的,捐赠者和公众可以实时查看捐赠收入、资金的去向,以及资金拨放情况,任何人都不能从中牟利。机构要求n个部门共同管理该地址,至少t个部门同意才能完成某笔资金拨出。
2.1 安全定义
本文方案的计算模型由n个成员组成,即{P1,P2,…,Pn}。成员间通过安全的点对点通道以及广播通道进行通信。假设S∈{1,2,…,n}是任意的成员集合,|S|=t。
敌手:假设敌手A是恶意且静态的。恶意是指敌手可以腐败其中k个成员,指示他们执行任意操作。并且本方案允许腐败成员的人数k达到n-1个(k=n没有意义)。静态是指敌手A必须在协议执行前选择腐败成员,敌手被要求在每轮的最后发言。
本文需要基于现有的比特币系统实现以下安全目标和要求:(1) 完全去中心化。整个方案完全不需要借助第三方,而是由成员交互完成密钥生成、分发、更新及数字签名等一系列协议。(2) 比特币地址的不可伪造性。在密钥生成协议中,敌手A无法伪造目标地址来欺诈诚实的成员。(3) 数字签名的不可伪造性。在选择消息攻击下数字签名具有不可伪造性。(4) 抵御合谋攻击。任意t个成员可以共同生成签名,而少于t个成员则无法生成签名。
2.2 方案描述
本文方案由密钥生成协议、密钥更新协议和数字签名协议三个协议组成。具体流程如图1所示。

图1 方案设计流程图
密钥生成协议用于生成密钥对和比特币地址。该协议必须先执行且仅需执行一次,而其他两个协议可重复执行。密钥更新协议不必在每次数字签名协议前执行(图中用虚箭头表示),当一方或多方的私钥发生泄露后,可通过执行该协议获取新私钥,但旧私钥必须被彻底销毁。数字签名协议需要在付款时执行,用于对相关比特币交易进行签名。收款时仅需向对方提供比特币地址。
2) 数字签名协议。(σ=(r,s))←Sig({ski}i∈S,m):集合S共同执行数字签名协议。每位成员Pi输入私钥ski和待签名的交易m,协议输出数字签名σ=(r,s)。然后向比特币网络中广播交易m和签名σ,等待矿工验证。
3 具体方案
当发生恶意成员拒绝广播消息或者拒绝打开承诺等情况时,本文方案中的协议均会立刻中止,且为了描述简洁,省略了对承诺方案的验证说明。
3.1 密钥生成协议
首先,全体成员利用t-1阶多项式:
f(x)=skmas+a1x+…+at-1xt-1modq
(5)
协议1KeyGen
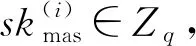
输出:成员Pi在本地保存(ski,Q,Adr)。

私钥生成:
(2) 接收并存储其他成员Pj的值KGCj。接着,成员Pi随机生成一个Zq上的t-1阶多项式:
(6)
(3) 当接收到其他所有成员Pj发送的值αj→i后,成员Pi先利用式(7)对该值进行正确性验证。
(7)
如果验证失败则立即中止协议,否则继续计算私钥:
(8)
公钥生成:
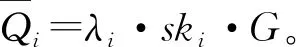


比特币地址生成:
(7) 否则,成员Pi继续计算比特币地址:
Adr=Base58(RIPEMD160(SHA256(Q)))
(9)
成员Pi在本地存储(ski,Q,Adr)。
3.2 密钥更新协议

协议2KeyUpdate


(1) 成员Pi随机生成一个t-1阶多项式:
(10)
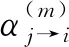
(11)
如果验证失败则立即中止协议,否则继续计算新私钥:
(12)
(3) 成员Pi计算:
(13)
(14)
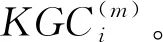
(6) 成员Pi更新私钥ski(m),并销毁旧私钥ski(m-1)。
3.3 数字签名协议

协议3Sig
输入:每位成员Pi输入私钥ski,公钥Q,用户IDi和待签名的比特币交易m。
输出:σ=(r,s)。

(2) 成员Pi选取一个随机数ρi∈Zp,然后向协议4-Mult输入两个值ki和ρi,集合S共同完成相关计算:
(15)
(3) 成员Pi在本地计算:
γi=m/t+λi·ski·r
(16)
然后向协议4-Mult输入两个值ρi和γi,集合S共同完成相关计算:
(17)
(4) 成员Pi在本地完成计算:
s=α-1·βmodp
(18)
得到签名σ=(r,s)。然后利用式(19)验证签名的正确性。
P′=s-1·m·G+s-1·r·Q=(x′,y′)
(19)
如果x′=rmodn,则证明签名有效,向比特币网络广播交易m和签名σ,否则中止该协议。
以下协议4参考文献[8]的6.2节。在执行该协议前,每个成员Pi需生成一个Paillier同态加密算法[21]的公私钥对(xi,yi),并广播其公钥yi。假设Enc表示pailler加密算法,Dec代表解密算法。Paillier的系数N>p22128。每位成员Pi操作具体如下。
协议4Mult
输入:每位成员Pi输入值ai和bi。
输出:值c。
(1) 成员Pi利用自己的公钥yi加密值ai,即计算wi=Encyi(ai),并生成一个非互动的零知识范围证明πi={ai (2) 当接收到来自成员Pj的消息(wj,πj)后,成员Pi先对πj进行验证。如果验证失败则中止该协议,否则随机选取一个数vi→j∈Zp22128,利用同态加密性质计算: wi→j=Encyj(di)=Encyj(aj·bi+vi→j) (20) 并生成一个非互动的范围证明: πi→j={aj·bi+vi→j (21) 然后将消息(wi→j,πi→j)传回给成员Pj。 (3) 当接收到来自成员Pj的消息(wj→i,πj→i)后,成员Pi先验证πj→i,如果验证失败则中止该协议,否则对wj→i进行解密: dj→i=Decxi(wj→i) (22) 当解密得到{dj→i}j∈S/{i}后,计算并广播: (23) 正确性分析。c值的计算公式为: 实现门限ECDSA最简单的方法是由可信经销商将已存在的密钥分为n份,然后分发给每个成员,而后t个成员即可通过将私钥份额交由该经销商完成数字签名。但该方法仍然存在可信第三方这一单点故障,更安全的方法则是完全实现去中心化,密钥生成、分发、数字签名等过程均由全体成员协作完成。下面具体说明本方案如何实现完全去中心化操作。 f(x)=skmas+a1x+…+at-1xt-1= (24) a(t-1,i)xt-1modq 生成n个相关秘密份额并完成分发工作。成员将对应的秘密份额进行累加得到私钥ski。 然后全体成员根据下式完成主公钥生成工作: 最后,每位成员可在本地利用主公钥Q生成比特币地址。整个密钥生成协议均是由全部成员共同完成的。 同理,在密钥更新协议中,私钥的更新算法与生成算法相类似,此处就不再赘述。需强调的是新私钥生成后,全体成员还需验证新私钥对应的主公钥Q(m)与原有主公钥Q是否一致,从而确定新私钥与原有比特币地址是否相关联。 在数字签名协议中,参与交易的集合S无须通过将私钥交由可信的第三方间接完成数字签名工作。但集合S需要协助完成如下计算: s=α-1β= (∑ki∑ρi)-1·(∑ρi∑(m/n+λi·ski·r))= (kρ)-1·ρ·(m+skmas·r)= k-1·(m+skmas·r) (25) 由式(25)可知,集合S联合生成的ECDSA的签名结果与集中式ECDSA相同。并且本文可以保证在协议的执行过程中,成员的私钥不会泄露。 证明:假设I⊆[n]为腐败成员集合。因为所有成员均被腐败证明是没有意义的,所以下面仅考虑I⊂[n](|I| (1) 集合J中的成员Pj随机选取一个值si∈Zq,然后计算Qi=si·G,[KGCi,KGDi]=Com(Qi),并广播KGCi,然后集合I执行相同操作。 定理2协议4-Mult满足输入的隐私性和不可区分性。 (2) 敌手A接收到的是成员Pj加密后的输入值wj=Encyj(aj),无法获知成员的输入值aj。 (3) 当接收到成员Pj返回的密文wj→i后,A解密得到的是{ai·bj+vj→i},但也无法从中获知成员Pj的输入值bj。 但本文强调由于Mult协议无法保证最后结果的正确性,所以在数字签名协议结束前,成员还需要利用公钥Q对生成的数字签名σ=(r,s)进行验证。当验证通过后,成员即可向比特币网络中广播交易等待矿工记入区块链中,否则需要重新执行签名协议进行交易。 基于Mult协议安全及ECDSA的SU-CMA安全性假设,可采用传统的归约模拟器方法证明本文的数字签名协议是SU-CMA安全的。 定理3Shamir门限方案的性质和数字签名协议的不可伪造性决定本方案至少t个成员才能生成数字签名,而少于t个则不能。 证明:不失一般性,假设t-1个成员试图伪造某笔交易的数字签名。 表1从四个方面将本方案与多重签名方案及文献[7]方案进行了对比。 表1 方案的特性对比 在多重签名方案中,同一个比特币地址需关联若干个固定数量的公钥,至少生成阈值个相关的签名才能花费该地址上的比特币。在门限签名方案中,一个比特币地址仅与一个公钥关联,团体按需生成或分割相关的比特币私钥,最终生成一个签名即可。虽然门限签名和多重签名均为多人参与的签名方案,但两者在比特币密钥管理中的应用效果有所不同。多重签名的优点在于仅需标准的ECDSA,每个签名可独立完成;而门限签名在访问策略结构上更具灵活性,且匿名性相对更强。因此,门限签名在比特币密钥联合管理的场景下适用范围更广。 从匿名性角度而言,将多重签名作为比特币交易的签名方案时,其内部访问控制策略将完全暴露给外界,这会严重损害团体的匿名性。而门限ECDSA的结果与常规ECDSA是完全无法区分的,可以避免多重签名的这一缺点,满足许多公司对于内部访问控制的保密需求。因此,本文方案可保证联合签名的匿名性与个体签名的匿名性一样强。 从去中心化角度而言,当某个人或团体希望将已有的比特币私钥进行分割管理时,则必须借助一个可信第三方。在文献[7]方案中,主账户利用基于属性的加密算法和Shamir门限方案对现有的私钥进行共享,从而实现整个公司对某个比特币地址上资产的细粒度管理。但其方案需要直接恢复私钥才能完成对交易的签名,因而只适合管理一次性地址。而本文方案的侧重点则是实现完全去中心化,允许各方以分布式方式生成或更新比特币私钥,且在签名过程中充分保证个体成员私钥的隐私性,而无须重新构建比特币主私钥,这更利于团体对某个固定比特币地址的长久共享。 从密钥更新角度而言,本文方案增设了密钥更新协议。全体成员可在每个时间周期内按协议规定更新自己的比特币私钥,而共享的主私钥不变。攻击者只有在某个周期内盗取阈值个数的比特币私钥份额,才能进一步恢复目标主私钥,盗取对应地址上的比特币。因此,密钥更新协议有效增大攻击者盗取成员私钥的难度,更适合于团体对某个比特币地址进行长期的联合管理。 从计算成本角度而言,多重签名中的每个成员都是以非交互的方式独立完成签名的。当成员并行完成签名时,签名的完成时间与单密钥ECDSA接近相同。本文方案和文献[7]方案均采用门限ECDSA对比特币交易进行签名,所以参与者的人数t是影响签名效率的重要因素。文献[7]方案是由主账户完成签名,参数t主要影响主私钥的恢复时间,而本方案的数字签名协议全程由t名成员交互完成,参数t影响整个协议的执行。表2就本文方案各个协议的主要开销进行了统计。 表2 本文方案的计算开销统计 在密钥生成和密钥更新协议中,成员的主要计算开销来自于椭圆曲线上的点乘运算、指数运算及基于承诺的零知识证明。因为在密钥生成阶段需要完成比特币地址的生成,所以该协议需要格外完成两个哈希运算。而数字签名协议是基于两次Mult协议运算的,表2先对Mult协议的主要运算开销进行统计,然后在此基础上统计签名协议的开销。该协议的主要开销来自于同态加解密算法以及其同态加性和乘性运算。 本文所提出的比特币密钥联合管理方案利用门限ECDSA实现对比特币的联合控制,并且成员私钥可进行定期更新。整个方案满足中小企业对于比特币密钥管理的安全需求,同时也为其他区块链项目中用户的密钥管理方案提供了新思路。
4 安全性分析
4.1 去中心化
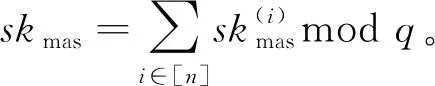
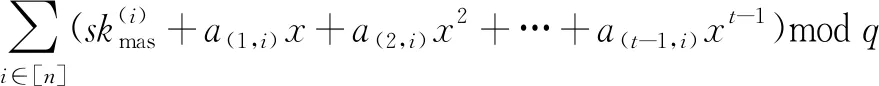
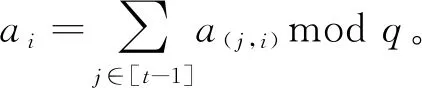
4.2 比特币地址的不可伪造性
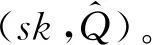
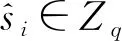

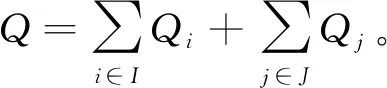
4.3 数字签名的不可伪造性
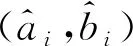
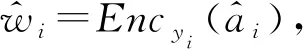

4.4 抵御合谋攻击
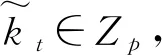
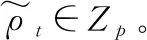


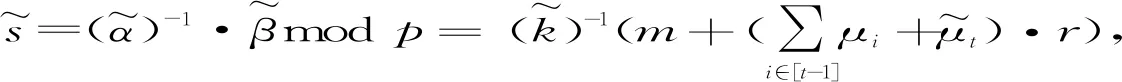
5 性能分析


6 结 语

