滚动时域估计在连续搅拌釜式反应器中的应用研究
王志飞 曾 静
(沈阳化工大学信息工程学院 辽宁 沈阳 110142)
0 引 言
随着经济的发展,大型复杂的化工过程在现代工业发展中日益增加,状态估计在化工领域也得到广泛的应用。近年来,随着对模型预测控制(MPC)的研究日益深入,基于滚动优化原理的滚动时域估计(MHE)也得到了广泛研究[1-4],MHE优势在于能够处理显式非线性系统和决策变量的约束。
MHE的基本思想是将估计问题转化为固定时域长度的优化问题,避免优化计算量随时间的增加而增加[5]。在MHE中,状态估计是通过在线求解一个最小误差平方和的优化问题来确定的。为了得到一个有限维度的问题,MHE的估计窗口一般选择为有限的。在采样时刻,当有新的测量值可用时,丢弃估计窗口中最旧的测量值,再次求解有限维的优化问题,得到状态新的估计[6]。MHE需要可靠的到达代价函数近似,虽然开发了不同的方法近似到达代价函数,包括文献[7]中的扩展卡尔曼滤波、文献[8]的无迹卡尔曼滤波和文献[9-10]中的粒子滤波,但通常确定带约束非线性系统的到达代价函数是一项困难的任务。
本文采用了扩展卡尔曼滤波近似到达代价函数的方法,针对连续搅拌釜式反应器及分离过程,在建立模型的基础上,设计该化工过程的滚动时域估计仿真实验,仿真结果表明该方法能够有效地处理化工过程中非线性系统的状态估计问题。
1 理论基础
1.1 系统描述
假设非线性系统的状态空间表达式如下:
(1)
式中:x∈Rn表示状态向量,且t=0时刻的状态为x0;w∈Rn是状态扰动向量;y∈Rn为输出测量值;v∈Rq表示测量噪声向量。为了简化讨论但又不失一般性,不考虑系统的输入。
假设系统状态x满足约束x∈X,其中集合X是凸集合。状态扰动w∈W,测量噪声v∈V是有界的,且:

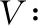
已知θ和θv为正整数,假设非线性函数f在X×W中满足局部Lipschitz条件,h在X中满足局部Lipschitz条件。本文进一步假设系统式(1)的输出y在同步时间瞬时采样{tk≥0},如tk=t0+kΔ,初始时间t0=0,Δ为固定时间间隔,k为正整数。
1.2 扩展卡尔曼滤波
扩展卡尔曼滤波(EKF)的基本思想是利用泰勒展开,将非线性方程直接线性化。线性化后的系统模型和系统实际模型存在一定的差别,非线性越强差别越大,但是EKF的优势不容小觑[11]。
上述系统的对应模型为:
x(k)=f(x(k-1),w(k-1))
z(k)=h(x(k),v(k))
(2)
线性化:
(3)
预测步骤:
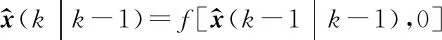
(4)
P(k|k-1)=F(k-1)P(k-1|k-1)FT(k-1)+
L(k-1)Q(k-1)LT(k-1)
(5)
增益:
K(k)=P(k|k-1)HT(k)×[HT(k)P(k|k-1)
H(k)+M(k)R(k)MT(k)]-1
(6)
更新步骤:
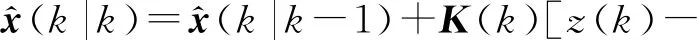

(7)
P(k|k)=[I-K(k)H(k)]×P(k|k-1)
(8)
1.3 滚动时域估计
对于上述系统式(2)的经典MHE(Moving horizon estimation)的标准表达式设计如下:
(9)
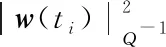
通常假设过程噪声w和测量扰动v取分段的常数值,采样时间为Δ,这样可以使上述问题成为有限维度问题,便于计算处理。对于一个过程而言,只要采样时间足够小,分段常数扰动和噪声能够适当地捕捉时变扰动和噪声对该过程的影响。
为了保证上述式(9)的最优解,只需要其中的代价函数最小。代价函数V(tk-N)在总结未包括在估计范围内的过去信息中起着重要的作用。到达代价函数的准确性不仅影响性能,而且还会影响MHE的稳定性,所以确定一个约束非线性系统的到达代价函数是一项艰难的任务。本文中的到达代价函数采用扩展卡尔曼滤波近似代替,形式为:
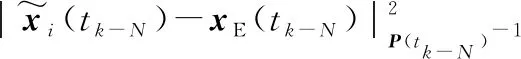
(10)
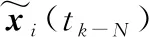
2 化工过程模型描述
滚动时域估计应用于连续搅拌反应器及分离过程,该过程模型包括两个相连的连续搅拌反应器(CSTR)和一个闪蒸槽分离器,如图1所示。

图1 循环流反应器分离工艺
详细的反应过程类似于文献[12]。第一个反应器的进料流中包含纯净反应物A,流速为F10,温度为T10。期望发生的反应是A转化为B,同时该过程也包含副反应B转化为C。从CSTR1端口流入CSTR2中的物料流的流速为F1,温度为T1,此外纯净的反应物A以流速F20和温度T20送入CSTR2,CSTR2中发生的反应与CSTR1相同。CSTR2的一部分出料物经过闪蒸槽分离器循环流入CSTR1,其流速为Fr温度为T3。每一个反应器装备有夹套,用于向反应器提供/输出热量。基于质量和能量守恒建立的标准模型,可以通过9个常微分方程来描述该反应过程的动力学:
xBrΔHvap2+xCrΔHvap3)
假设分离器中发生的反应量可以忽略不计,并且每个组分的相对挥发性在工作温度范围内保持不变。与闪蒸罐中液体成分相关的顶流成分建模代数方程描述如下:
(11)
过程涉及到的变量含义、参数的值详细介绍如表1和表2。注意,反应(1)和反应(2)分别指A→B和B→C的化学反应。

表1 反应器的过程变量

表2 反应器过程参数

续表2
3 仿真设计与结果
3.1 仿真设计
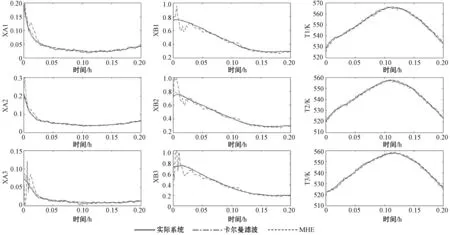
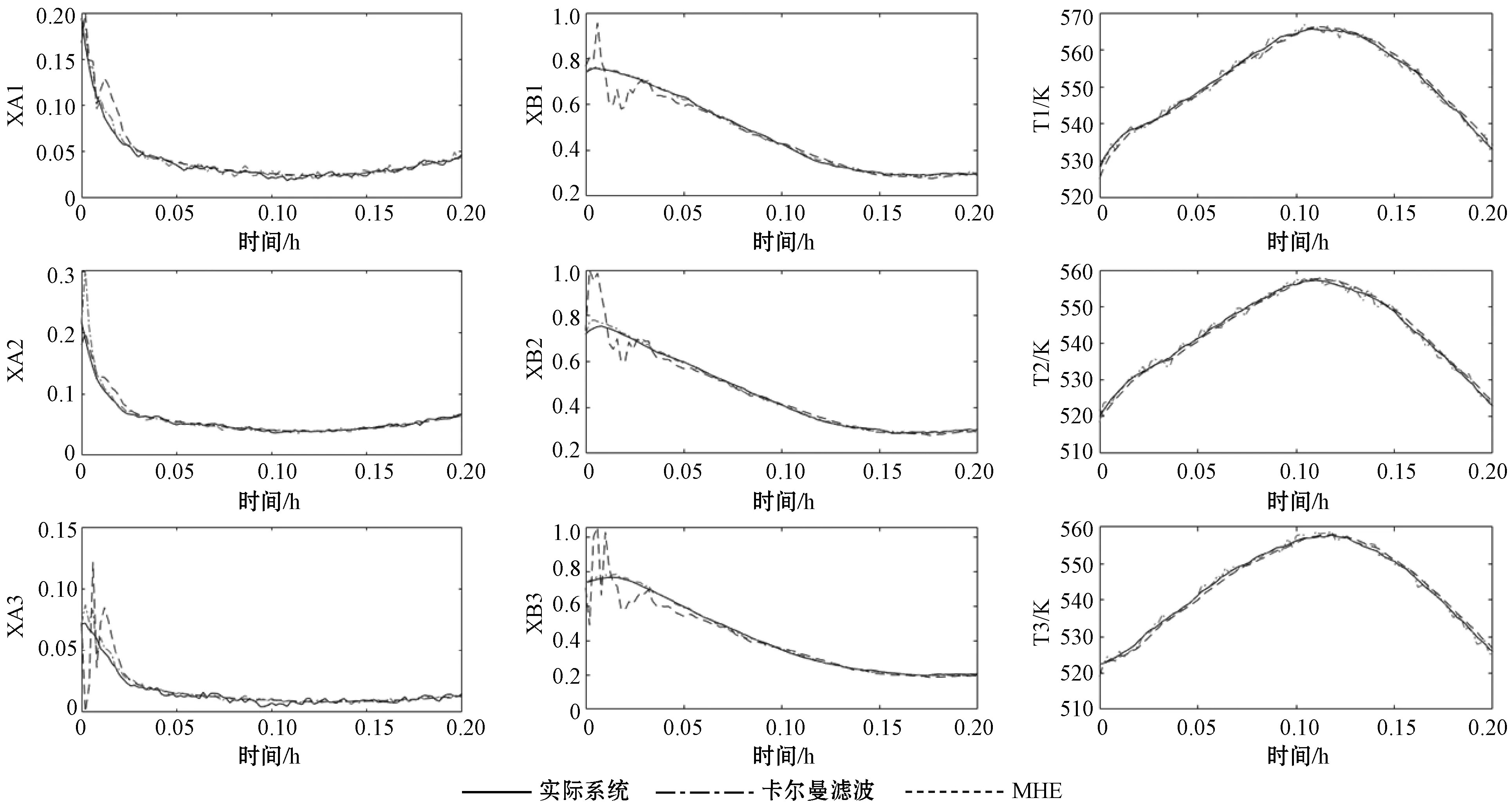
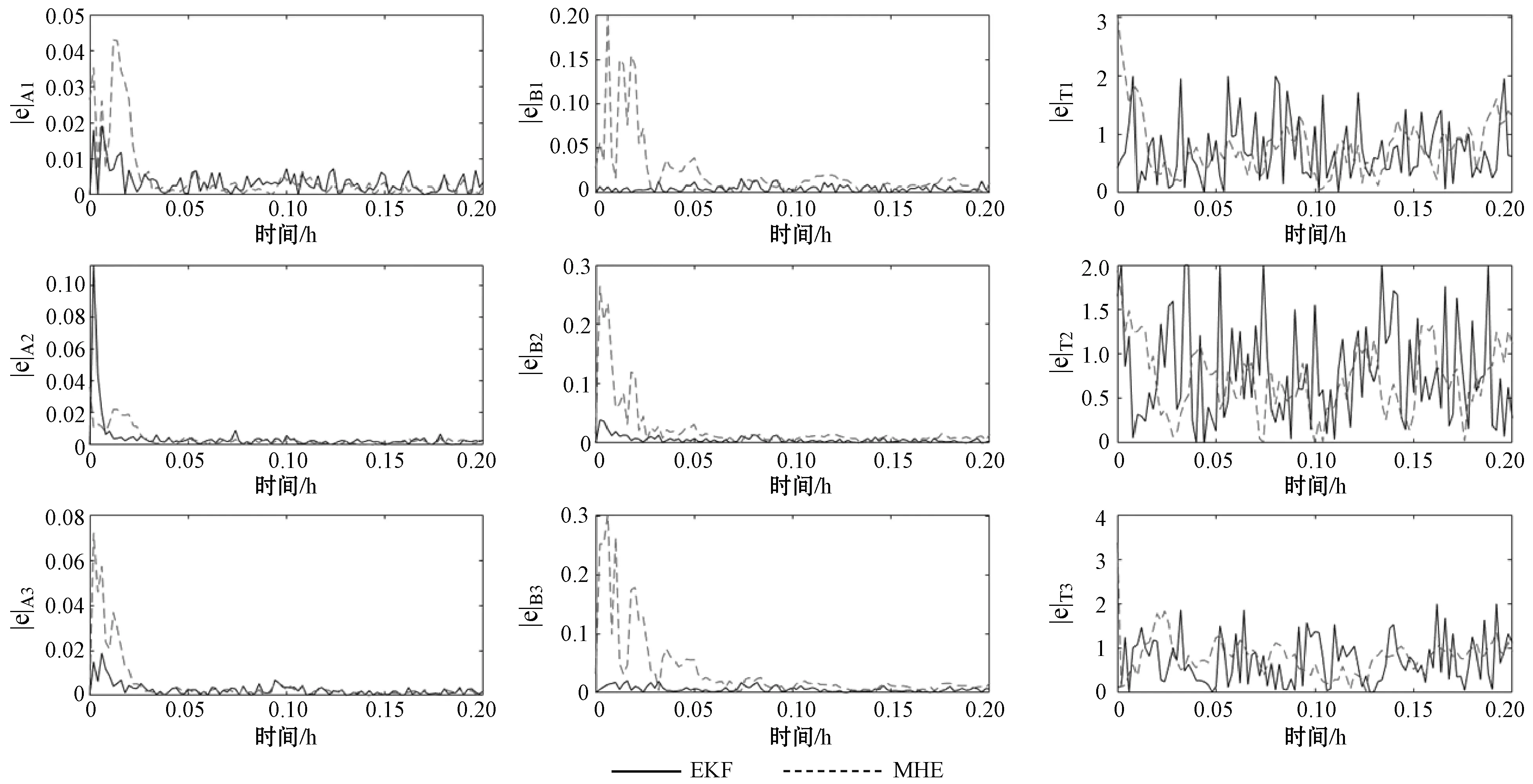
本节设计了扩展卡尔曼滤波和MHE的仿真实验,通过对比来说明状态估计性能的优劣。在仿真设计上,采样时间Δ=0.002 h,系统状态的界限约束在0 x0=[0.193 9, 0.740 4, 528.348 2 K, 0.216 2, 0.719 0, 520.064 9 K, 0.071 6, 0.737 3, 522.376 5 K]T 初始估计值为: 522 K, 0.072, 0.705, 519 K]T 当N=20和N=30时,MHE和扩展卡尔曼滤波的轨迹分别如图2、图3所示。然后本文分别计算了EKF和MHE在各采样时刻与实际状态的误差,结果如图4所示。 图2 N=20时各状态变量轨迹图 图3 N=30时各状态变量轨迹图 图4 N=30时各状态误差轨迹图 由图可见,在区间0~0.05 h,MHE的轨迹波动幅度较大,考虑到在状态估计的初期MHE的估计窗口数据的不完整,造成估计的误差较大,故可以忽略该段时间内对估计性能的影响,理想的MHE估计性能主要参考区间为0.05~0.2 h。 从图2和图3中可以看出扩展卡尔曼滤波和MHE都能够很好地追踪系统的实际状态。对比图2、图3中MHE的各状态轨迹表现的更加平滑,波动较小。说明了随着滚动窗口N的增大,MHE的估计效果也会更好,但是滚动窗口的增加,计算量同样也会增加,仿真时长也会相应延长。 然后,为了比较扩展卡尔曼滤波和滚动时域估计的效果,算出了EKF和MHE与实际系统状态的误差平均值,如表3所示。 表3 状态估计误差平均值 计算方法如下: 滚动时域估计作为一种有效的状态估计方法对复杂工业过程的控制与优化产生了巨大的影响。本文将扩展卡尔曼滤波和滚动时域估计方法引入到连续搅拌釜式反应器的状态估计问题中,将非线性系统的估计问题转化为滚动时域的最优值问题,合理地处理非线性系统的估计问题。仿真结果表明了针对有约束非线性连续搅拌釜式反应器及分离过程,扩展卡尔曼滤波及滚动时域估计方法都能有效估计出系统真实状态。通过对状态估计误差平均值的进一步比较,说明滚动时域估计效果要优于扩展卡尔曼滤波,且随着滚动窗口的增大,MHE的估计效果也会更好。
3.2 结果分析

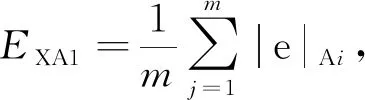
4 结 语

