深度研读教材策略四：探寻数学知识的实用价值

崔晶磊 李惠萍

【导读】

“分段计费”是人教版数学五年级上册第16页例9的教学内容。“分段计费”是生活中常见的数学问题，看似简单，教学起来却非常难：有时候分两段，有时候分三段;有时候的基础价是“包干”的，有时候不“包干”;超出价的计价数量，有时候取整，有时候不取整……

简简单单的一个收费问题，为什么要搞那么复杂呢？这其中有什么奥妙？来自昆明市盘龙区金康园小学的崔晶磊老师，从函数渗透和社会公平的角度，为我们带来了不一样的教学思路。从崔晶磊老师执教的过程中，我们可以看出数学对于维持人们生活秩序的重要性。

【案例】

课堂实录：

一、梳理条件，初步建模

师：同学们，你们知道吗，出租车在很多地方都被叫作计程车……

师：出示教学图片，数学课本上的例9。（根据后面的课程设计，将例9中6.3千米改为5.3千米）

师：请同学们观察这幅图，你们从图中能找到哪些数学信息？

生1：3 km以内7元。

生2：超过3 km每千米收费1.5元，不足1 km按照1 km计算。

生3：路程5.3 km应该看作6 km。（教师板书）

师：那现在老师打了一张出租车，出租车行驶了1千米，我该付款多少钱？

生：7元。

师：那出租车行驶了2.1 千米呢？

生：7元。

师：出租车行驶了2.9 千米呢？为什么？

生：还是7元。因为根据条件“3 km以内7元”。

师：现在出租车行驶了4千米，我下车了，这时候我该付款多少钱？怎么计算？

生：8.5元，根据条件“超过3 km每千米收费1.5元”，超出了1千米，所以要增加付款1.5元，加上“起步价”就是8.5元。

师：题目中李叔叔的行驶里程是5.3千米，该怎么付费呢？能用线段图表示吗？

……

师：请你给我们讲述一下你的想法。

生1：我先画了3 cm表示前3千米收费7元，再画了2.3厘米表示后面超出的部分每千米收费1.5元。

师：你说得非常好，大家都是这么画的吗？有没有哪位同学的作品和他不一样？

生2：我画的是6 cm的线段，因为有一个条件是“不足1千米按照1千米计算”。

师：哪位同学最懂他？

生3：李叔叔打车一共行驶了5.3千米，根据条件“不足1千米按照1千米计算”应该把这个小数看作一个整数来计算。

师：为什么要取整数？

生1：計算起来麻烦。

师：如果在临时停车点计算这么麻烦的费用就会……

……

师：所以，取整数是为了更加方便地付费，节约时间。

师：那把一整段分成两段又怎么理解？

生4：3千米以内和超过3千米的收费不一样。

师：能不能给两个部分分别起一个名字？

（板书：基础价 超出价）

师：现在能算一算总价了吗？能否使用一个公式来解决？

生：基础价+超出价=总价

师：能列算式计算了吗？试一试。

二、循序渐进，深入感知

（一）初识函数，埋下一颗数学的种子

师：同学们，老师昨天也画了一张图，大家看看。横着的这一条叫做横轴，表示行驶的里程，竖着的这一条叫做竖轴，表示价格，同学们可以相互交流，最后告诉我，你的想法。

生：黄色的线表示3千米以内，白色的线表示超出的部分。

师：你说得非常好，（教师手指横轴0-3任意位置）（多次），那走这么远呢？

生：7元。

师：那3千米以内7元的意思是？

生：只要是车子启动不超过3千米，就要付7元。

师：那正好3千米呢？（教师手指横轴3）

生：还是7元。

师：所以3千米以内7元包含了……？

生：3千米。

师：所以我用一个实心黄色圆点表示。那上面的空心圆点表示？

生：刚好3千米还没有超出。

师：咱们再来看看白色的线，谁懂它的意思？

生1：白色的线表示超出的部分，每多行驶1千米，就要增加1.5元。

师小结：同学们，通过这幅图我们又从另外一个视角看到了今天要解决的问题“分段计费”，在整个打车的过程中，有两种计费方式，我们要分开计算。

（二）纵向挖掘，透彻领悟

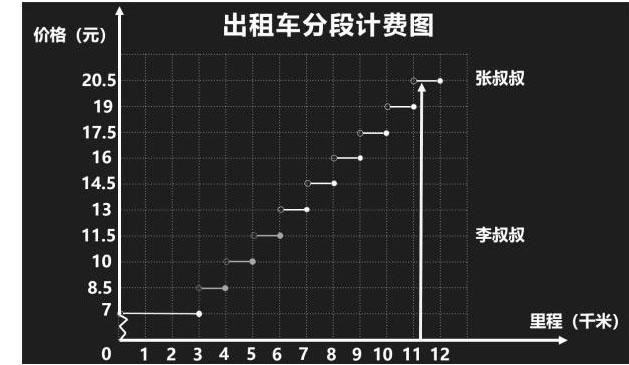
师：同学们，张叔叔也打出租车了，他的行驶里程是11.2千米。不计算，你能从图象上找到答案吗？

生：20.5元。

师：怎么如此迅速，快起来说说。

生：11.2在11和12的之间，根据条件不足1千米按照1千米计算，所以11.2千米应该收费是20.5元。

师：那张叔叔打车走了11.5千米，应该付多少车费呢？11.9千米呢？11.95千米呢？

生：都是20.5元，因为不足1千米要按照1千米计算。

师：对比张叔叔和李叔叔的路程与车费，你有什么发现？

生：我发现打车的路程越长，车费就越多。

师：张叔叔的车程是李叔叔几倍？

生（齐）：2倍。

师：那张叔叔打车的费用也是李叔叔的2倍吧。

生：不是，李叔叔花了11.5元，张叔叔花了20.5元，不是2倍。

师：怎么会这样呢？计价里程明明就是2倍关系啊？

生：我想应该是总价中包含了基础价，所以它们不成倍数关系。

师：说得非常好！你们真的太厉害了。基础价和超出价哪个更贵？

生（齐）：基础价。

师：在李叔叔和张叔叔的打车费中，基础价所占的分量如何？

生1：李叔叔的车费中，基础价占到了一半，所以比较贵。

师追问：张叔叔的呢？

生2：基础价占不到一半。

师：也就是便宜的部分……

生2：占的比较多，所以总体上更划得来。

师：这就是说，打车路程越短……

生（迫不及待）：越不划算。

师：为什么要这么规定呢？

……

师：对了！之所以把出租车收费弄得那么复杂，就是为了促进社会的公平性。

（三）拓展提升，将生活中的问题“还给”生活

师：同学们，生活中还有哪些地方在使用分段计费？

生：水费、电费、停车场收费……

师：你们觉得分段计费的方法公平吗？为什么？

生：公平。

师：是的，分段计费就是为了让更多的人享受到公平的待遇。

……

师：那么所有分段计费中的“基础价”都比“超出价”更贵吗？

生1：不是，水费就是“超出價”更贵。

师：为什么呢？

……

（四）全课小结，设疑思考

师：是的，分段计费是对计费方式进行人为干预的一种消费模式。希望同学们去发现生活中更多分段计费的例子，体会数学给生活带来的更多价值。

板书设计：

【评析】

本节课是昆明市李惠萍数学名师工作室和盘龙区周佳泉数学名师工作室合作、研讨的成果结晶，经过多次磨课后初步形成的“雏形”，最终由崔晶磊老师完善并执教。本节课在以下几方面做出了一些新的尝试和突破：

1.不断深化对数学模型的理解。这是一节容易被简单化的课，在实际教学中，部分老师和学生仅止步于会应用“基础价+超出价”求出问题答案，却没有对这一问题模型中的细节进行深度关注：在“基础价”中，“3千米以内”究竟是指几千米？在超出价中，学生是否真正理解“不足…按照…”这个条件？——是否所有“超出价”的计价数量都是按照这个方法取整？总体来讲，车程越长付费越多，但付费是否与车程长的增长成倍数关系（六年级学的正比例关系）？这些关键细节的忽略，无疑会使本节课的价值大打折扣。从这节课的实际操作可以看出，关注这些细节，对于学生深入理解“基础价+超出价”这一数学模型的本质和实际应用的范围、边界，无疑是大有裨益的。

2.用动态的眼光看待世界。“3千米以内收费7元”这句话的含义，对于小学生来说无法用静止的观点去准确描述。它必须用动态的观点举例说明——从0千米至7千米（包括“0千米”和“7千米”这两个点）在内的任何一个车程点下车，都是收费7元。对于学生以往的数学学习经验来说，这是第一次出现的“奇葩”问题，但是结合生活实际却非常容易理解，哪怕你只坐上出租车就立即下车，你也“耽误”了出租车司机的一单生意，应该给予人家补偿，所以仍然要付费7元。而在“超出价”的车程计数中，如果不“取整”就会给计算带来很大麻烦，一些临时停车点的停车时间就会超时，造成交通拥堵。因此，分段计费问题在图象上，表现为分段函数的形式。

3.体会分段计费的公平价值。“3千米以内收费7元”的规定看似不合理，却对那些随意打车的人做出了行为限制，让他们在“不划算”的心理压力下，选择其他更适宜的出行方式，把出租车的服务提供给真正有需要的顾客。而同样是分段计费，“阶梯水费”“阶梯电费”的基础价为什么不实行“包干”价呢？学生根据自己的实际经验，很快有了正确答案——如果“阶梯水费”“阶梯电费”的基础价也实行“包干”价的话，那就会促使本来用不了那么多水和电的小额用户大量用水和用电——反正都要收那么多钱嘛！这就反而造成了浪费。由此可见，出租车计价当中的“基础价”规定偏高，正是为了限制低消费，促进出租车业务流向有真正需要的消费群体;而“阶梯水费”“阶梯电费”等收费规定中“超出价”偏高是为了限制高消费，促进社会厉行节约良好风尚的形成。

“分段计费”这节课，教好数量关系（即数学模型）已属不易，再加入函数思想的渗透，从而深入理解分段计费的人为干预特性和它在促进社会公平中的巨大价值，无疑就使得这节课的内涵更加丰富了。