低碳视角下改进DMBSO算法的垃圾收运路径优化

周双牛，李 稚*，王 喆

(1.天津工业大学经济与管理学院，天津 300387；2.四川旅游学院经济管理学院，成都 610100)

近年来，随着中国经济社会的发展，城市生活垃圾的产生量也迅速增加。据统计，2019年全国337个一至五线城市生活垃圾生产量约3.43亿t，“垃圾围城”现象成为城市发展的“痛点”。相关研究表明，生活垃圾的收集和运输的物资消耗占整个垃圾处理系统的70%～80%，同时，在低碳环保理念下，合理的生活垃圾收运路线能够有效降低碳排放量，故对城市生活垃圾收运路线进行优化，具有重要的实践意义。

低碳视角下城市生活垃圾收运路径优化问题属于绿色车辆路径问题(green vehicle routing problem, GVRP)，已经证明其是典型的NP-hard问题[1]。城市生活垃圾收运路径优化问题成为VRP应用的新趋势，中外已有部分专家对其进行初步研究。Hoang等[2]将人工神经网络废物预测模型和地理信息系统垃圾收集路线优化相结合，以确定行驶距离最小的最佳垃圾收集路线，该研究虽能够找到最佳路线，但由于其计算复杂，只适用于垃圾回收点数量较少的情景。Ilona等[3]提出了任务路径优化的两阶段方法，在第一阶段生成任务，在第二阶段将任务分配给车辆，并基于遗传算法提出新的求解方法，用于优化分配问题，最后用实例验证了算法的优越性。Afroditi等[4]建立以最小化行驶时间和成本为目标的车辆调度模型，并对禁忌搜索算法进行改进，以期提高垃圾收集管理的效率。近几年，垃圾处理问题愈发严重，中国相关专家也对此展开研究。张爽等[5]考虑垃圾上门收运模式，建立基于居民满意度的垃圾上门收运路线模型，并运用人工鱼群算法进行求解，通过仿真实验验证了算法的有效性。朱海红等[6]建立了城市垃圾回收路径规划模型和无线传感网络模型，设计了基于差分进化和局部邻域搜索的量子布谷鸟搜索算法，并与量子布谷鸟搜索算法和遗传算法进行比较，最优解和平均解均有所提高。

求解车辆路径优化问题主要有精确算法和元启发式算法，精确算法包括分支定界法、割平面法等，但由于其求解过程复杂，难以适用于大规模组合优化问题[7]，而元启发式算法具有高效、并行等优点，被广大专家用来求解复杂的组合优化问题。头脑风暴优化算法(brain storm optimization, BSO)是Shi[8]于2011年提出的一种新型智能优化算法，后有许多学者对其进行应用和深入研究。杨玉婷等[9]提出了一种基于讨论机制的BSO算法，增加新个体的产生机制，使局部搜索和全局搜索达到动态平衡。Cheng等[10]提出新型保持种群多样性策略，避免该算法陷入局部搜索。头脑风暴优化算法在函数优化[11]、医学检测[12]、图像识别[13]等领域有了一定的研究和应用，其在垃圾收运路径问题上是一个新的研究视角。

综上所述，已有成果为进一步研究垃圾收运路径问题奠定良好的基础，但仍存在一些不足。

(1)现有研究大多以使用车辆最少[4]、成本最小[5]、总运输距离最短[6-7]等为目标，建立单目标模型并求出最佳路线，但均未考虑环境指标。

(2)现有成果一般是根据车辆行驶距离以代替最低碳排放量[14-15]，但实际运输中还应考虑车辆载重情况对碳排放量的影响。

在前人研究的基础上，通过对垃圾收运过程中影响因素的研究，建立以最短路径和极小化碳排放量为目标的绿色垃圾收运路径优化模型，在前人对BSO算法研究的基础上，引入逆转算子、启发式交叉算子和精英保留策略，以实现最优的垃圾收运路径规划。

1 双目标绿色垃圾收运路径模型的构建

1.1 模型的描述与假设

绿色垃圾收运路径优化问题可以描述为:由一辆或多辆统一车型的垃圾运输车辆从垃圾分拣中心出发，依次经过若干个垃圾存放点，直到把所有垃圾存放点的垃圾运输完为止，运输车辆返回垃圾分拣中心。优化目标是在运输车辆装完所有收集点垃圾的前提下，行驶总路线最短且产生的碳排放量最少。

垃圾收运问题在实际生活中影响因素较多，为方便研究且不失科学性，做以下假设。

(1)当前研究区域内，只有一个垃圾分拣中心和n个垃圾存放点，且每个垃圾存放点的位置和垃圾产生量已知。

(2)每条回收路线中，垃圾存放点不能被重复回收。

(3)运输车辆最大载重固定且无超载现象。

(4)运输过程中不存在堵车现象且车速恒定。

1.2 主要符号说明

文中所用主要符号说明如表1所示。

表1 主要符号说明

1.3 数学模型的构建

1.3.1 目标函数

由于路径最短的路线不一定是碳排放量最小的路线[16]，故本文模型目标在保证求得最短路径目标的前提下，使其碳排放量最小。最短路径为运输车辆遍历每个垃圾存放点，所经过距离总和最小，本文两节点之间的距离使用欧氏距离。碳排放量的影响因素较多，直接影响因素有:车辆载重、行驶速度、道路角度、道路路面条件等。本文中不考虑客观因素对碳排放的影响，主要考虑车辆载重和行驶速度等可控因素。

碳排放量计算方法可根据Zhang等[17]碳排放量的测算方法，并借鉴欧盟委员会提出的估算运输过程中的排放量方法(methods for estimating emissions during transportation, MEET)计算碳排放量ε与车辆行驶平均速度v的关系，此模型包含碳排放量估计函数、道路坡度修正因子、载重修正因子等，即

(1)

式(1)中：参数k、a、b、c、d、e、f为与车辆、燃料类型等相关的系数，当车辆自重小于3.5 t、燃料为柴油时，参数k、a、b、c、d、e、f的取值依次为429.51、-7.822 7、0.061 7、0、0、0、0，故两节点之间的碳排放量εij=[dij(k+av+bv2)/1 000]e0。

1.3.2 双目标绿色垃圾收运路径模型描述

(2)

εij=[dij(k+av+bv2)/1 000]e0

(3)

(4)

(5)

(6)

qij≤Qzij

(7)

(8)

qij≥0

(9)

i,j=1,2,…,n

(10)

式(2)为目标函数，表示最短路径和极小化碳排放量；式(3)为垃圾运输车从节点i到节点j的碳排放量；式(4)表示确保每个垃圾存放点仅被回收一次；式(5)表示车辆到达该垃圾存放点，并且必须从该节点离开；式(6)表示装载完某存放点垃圾后，车辆载重量的增加量与该节点的垃圾产生量相等，此约束可避免产生巡回运输等非正常情况；式(7)表示车辆在节点i和节点j之间的载重不能超过最大运载量Q，且当车辆不经过(i,j)时，该段载重量为0；式(8)表示车辆遍历完每个垃圾存放点后，回到垃圾分拣中心；式(9)和式(10)为变量的取值约束。其中当i(或j)=1时，表示垃圾分拣中心，i(或j)=2～n时，表示垃圾存放点。

2 模型的算法设计与实现

随着人工智能的兴起，越来越多的智能算法应用于求解组合优化问题。头脑风暴优化算法是一种基于人类创造性解决问题过程的群体智能算法，在解决经典优化算法难以求解的大规模高维多峰函数问题时显示出其优势，BSO算法相较于其他智能优化算法有更好的求解效果，在迭代次数更少的情况下求得最优解，并且有更好的稳定性。

2.1 标准BSO算法

头脑风暴优化算法不依赖于问题的初始解，具有较好的快速收敛和全局搜索能力，其基本思想是:首先通过聚类的方法对所有个体进行分类，然后利用类之间个体的分布进行更新操作，进而产生一系列新个体，对更新过程不断进行迭代，最后求出最优解，标准BSO算法具体流程如下。

步骤1 初始化种群。

步骤2 评价每个个体并进行聚类操作。

步骤3 利用更新机制产生新个体。

步骤4 新个体与旧个体进行比较，择优保留，并更新种群和聚类中心。

步骤5 判断是否达到最大迭代次数，是则输出最优解，否则转到步骤2继续迭代。

标准BSO算法使用K-means方法进行聚类，并将每类的最优个体作为该类的聚类中心。在产生新个体时，使用高斯变异公式对个体进行更新，即

(11)

(12)

式(12)中：logsig为S型对数传递函数；maxgen为最大迭代次数；gen表示当前迭代次数；K表示动态调整全局搜索和局部搜索的速度；rand表示产生(0,1)之间的随机数。

2.2 解的构造

可行解的好坏影响着算法的优劣，本模型解的构造如下:首先固定1为起始位置，然后随机生成一个2～n不重复的数组，从垃圾分拣中心1位置开始，依次计算数组中各垃圾存放点的垃圾产生量，若已经过存放点的垃圾产生量之和加上下一个存放点的垃圾产生量仍未超过车辆最大载重，则可以经过下一个存放点，否则，车辆需要返回垃圾分拣中心进行卸载，然后去存放点，直至遍历所有垃圾存放点，最终返回垃圾分拣中心。例如，随机生成数组(1,7,4,12,8,9,6,2,3,5,10,11,1)，将其进行编码为(1,7,4,12,1,8,1,9,6,2,3,5,1,10,11,1)，编码后的数组中间的“1”表示此时车辆的可装载量小于下一个存放点的垃圾产生量，需要返回分拣中心进行卸载。

2.3 启发式交叉算子

经典的交叉算子存在很大的随机性和盲目性，在交叉过程中只是数字的组合，并未考虑实际意义，故使用启发式交叉算子，在基因层面设置选择规则，将个体层面的寻优原则延伸到基因片段，在每一次的启发式交叉操作过程中，对每一个基因的选择都进行评估，以便能够保留父代的全部优秀基因，有效提升了算法效率。启发式交叉算子分为右侧寻找和左侧寻找两种子代生成方式，以左侧寻找为例，如图1所示，蓝色为选择父代的基因，具体步骤如下。

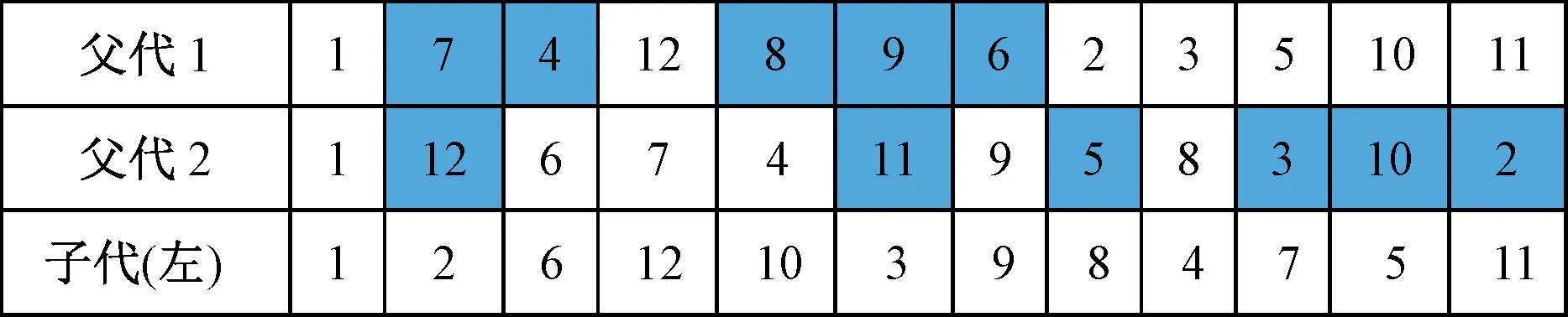
图1 启发式交叉算子示意图

步骤1 生成1×n维大小的零矩阵。

步骤2 选择1为当前基因，子代待更新位置pos初始化为2。

步骤3 分别计算并比较父代1和父代2中当前节点到其左侧紧邻节点的适应度值，选择适应度值大的节点作为pos位置的基因，若父代个体当前基因为末位基因，则选择节点1为其左侧基因。

步骤4 更新当前子代基因和pos。

步骤5 若路径构造完整则结束，否则返回步骤2进行循环。

2.4 逆转算子

逆转算子在保证种群多样性的同时，能够将个体中的优秀片段保留下来，具体操作为:首先选择两处个体断裂位置，然后将断裂部分取出并进行逆转，最后插入到个体断裂位置。例如，个体(1,7,4,12,8,9,6,2,3,5,10,11,1)经过逆转操作后，子代为(1,7,9,8,12,4,6,2,3,5,10,11,1)。在算法后期，能够得到大量优秀个体，若使用交叉算法，则会破坏个体中的优秀基因，逆转算子能使子代继承亲代的更多信息，因此其搜索最优解的能力强于交叉算子。

2.5 精英保留策略

为避免启发式交叉、逆转操作丢失和破坏更新后种群中的精英个体，故采用精英保留策略使运算过程中的精英个体得以保留到下一代。精英保留策略的核心思想是在种群进化过程中出现的精英个体保留到下一代中，使算法在更少的迭代次数内收敛到全局最优解，并且在迭代后期不会跳出最优解。本文算法为避免适应度强的个体被淘汰，故保留前30%的精英个体。

2.6 改进DMBSO算法的实现

基于讨论机制的头脑风暴优化(discussion mechanism based brain storm optimization, DMBSO)算法在标准BSO算法中引入组间讨论和组内讨论机制，在算法运行前期主要进行组间讨论，增加种群多样性，使算法能够跳出局部最优解，后期重点进行组内讨论，在优秀个体附近搜索全局最优解。为解决离散组合优化问题，在DMBSO算法上对其更新方式进行较大改进，并且将算法步骤进行完善，弥补了算法后期跳出全局最优解的缺陷。改进DMBSO算法的具体流程如图2所示，操作步骤如下。

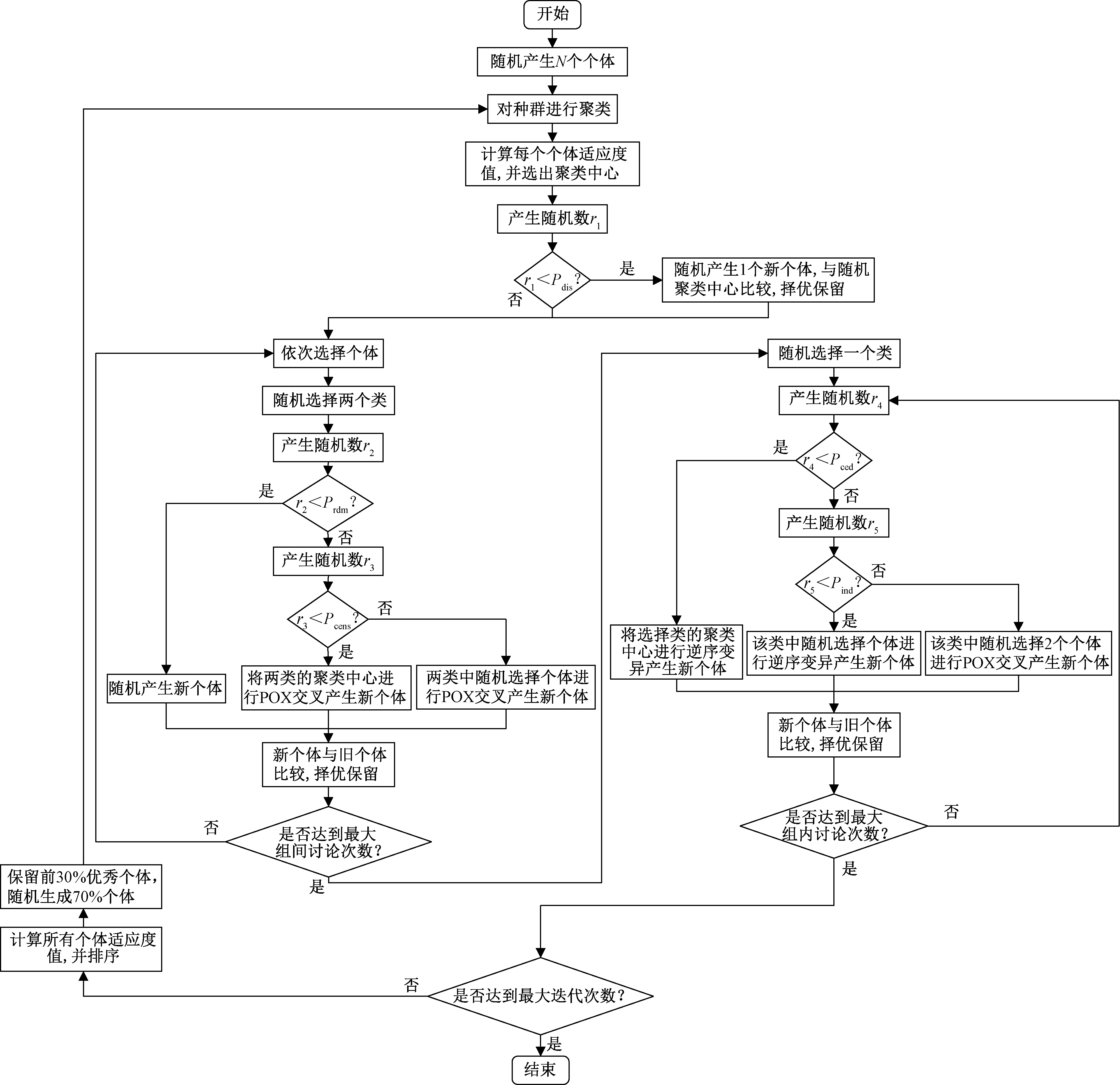
图2 改进DMBSO流程图

步骤1 初始化参数和种群。

步骤2 对种群的适应度值进行聚类。

(1)计算每个个体适应度值，对适应度值进行K-means聚类，并将各类中的个体排序，其中最佳个体作为该类的聚类中心。

(2)产生一个随机数r1∈(0,1)，若r1小于概率参数Pdis，则进入操作(3)，否则进入步骤3。

(3)在K类中随机选择一个类的聚类中心，并随机生成一个新个体。

(4)计算新个体适应度，若优于旧个体适应度，则将旧个体替换，否则淘汰新个体。

步骤3 进行组间讨论。

(1)随机选择两个类，并产生随机数r2∈(0,1)。

(2)若r2小于概率参数Prdm，则随机产生一个新个体，否则进入操作(3)。

(3)产生一个随机数r3∈(0,1)，若r3小于概率参数Pcens，则选择两类的聚类中心作为两个父代个体，进行启发式交叉操作产生子代个体，否则进入操作(4)。

(4)在选择的两类中，分别随机选择一个个体，将二者作为父代个体，进行启发式交叉操作产生子代个体。

(5)计算子代个体适应度，并与父代个体适应度比较，保留较优个体。

(6)判断是否达到最大的组间讨论次数。

步骤4 组内讨论。

(1)依次选择每一个个体，记为当前个体。

(2)产生一个随机数r4∈(0,1)，若r4小于概率参数Pcen，将当前个体所在类的类中心进行逆转操作，产生新个体，否则进入操作(3)。

(3)产生一个随机数r5∈(0,1)，若r5小于概率参数Pind，在当前个体所在类中随机选择一个个体并进行逆转操作，产生新个体，否则进入操作(4)。

(4)在当前个体所在类随机选择两个不同个体，并对将这两个个体进行启发式交叉产生新个体。

(5)计算新产生个体的适应度，并与旧个体适应度进行比较，保留较优个体。

(6)判断是否达到最大的组内讨论次数。

步骤5 精英保留策略。

对当前群体按适应度值进行排序，保留前30%的优秀个体，并产生70%的新个体，使种群容量保持不变。

步骤6 判断是否达到最大迭代次数，是则结束，否则进入步骤2继续迭代更新。

上述步骤中的概率参数Pdis、Prdm、Pcens、Pcen和Pind参照文献[9]的研究成果，分别取值为0.2、0.5、0.7、0.6和0.5；步骤2中的操作(4)，将随机产生个体的适应度与旧个体适应度比较，能够有效避免算法迭代后期跳出最优解；每一代中，步骤3组间讨论和步骤4组内讨论的讨论次数设置为动态取值，组间讨论次数设为单调递增函数，如式(13)，组内讨论次数设为单调递减函数，如式(14)，此操作能够使算法，在开始阶段加强全局搜索，寻找潜在的全局最优解，在搜索后期，主要进行细致搜索，加速收敛。

Ntex=Nmt(1-gen/maxgen)

(13)

Ntin=Nmt(gen/maxgen)

(14)

式中：Ntex为当代最大组间讨论次数；Ntin为当代最大组内讨论次数；Nmt为组内讨论和组间讨论次数的最大值；gen为当前迭代次数；maxgen为最大迭代次数。

3 仿真实验与分析

3.1 标准算例仿真实验

为验证改进DMBSO算法的求解性能，从Solomon数据集中选取标准算例进行仿真。为了更加具有客观性，分别从Solomon数据集中客户数为25、50、100的三种问题规模中选取C101类、R101类和RC101类9个算例。实验仿真环境为Windows10操作系统、Intel(R)Core(TM)i5-5200U CPU @ 2.20 GHz处理器，4 G内存，仿真软件为MATLAB2019b。选取BSO算法和ACO算法进行实验对比，设置算法初始参数为:种群规模N=100，聚类数目cluster_num=6，最大迭代次数maxgen=50，车辆最大载重cap=1，蚁群算法中的α=1、β=5，信息素蒸发系数ρ=0.75，信息素增加强度系数Q=10。三种算法分别对9个算例运行20次，运行结果如表2所示。

由表2可知，在9个标准算例中，改进DMBSO算法的性能最优，其次是BSO算法，而ACO算法的表现最差。在min、avg和var三个方面，改进DMBSO算法和BSO算法均明显优于ACO算法，而改进DMBSO算法相对与BSO算法来说，在问题规模较低情况下两者差距不大，当问题规模较高时，改进DMBSO算法能求到的最小值更优，平均值方面也表现优异。在var方面，问题规模越高，问题复杂度越大，求解效果显得不稳定，符合客观事实，且改进DMBSO算法的稳定性更好。

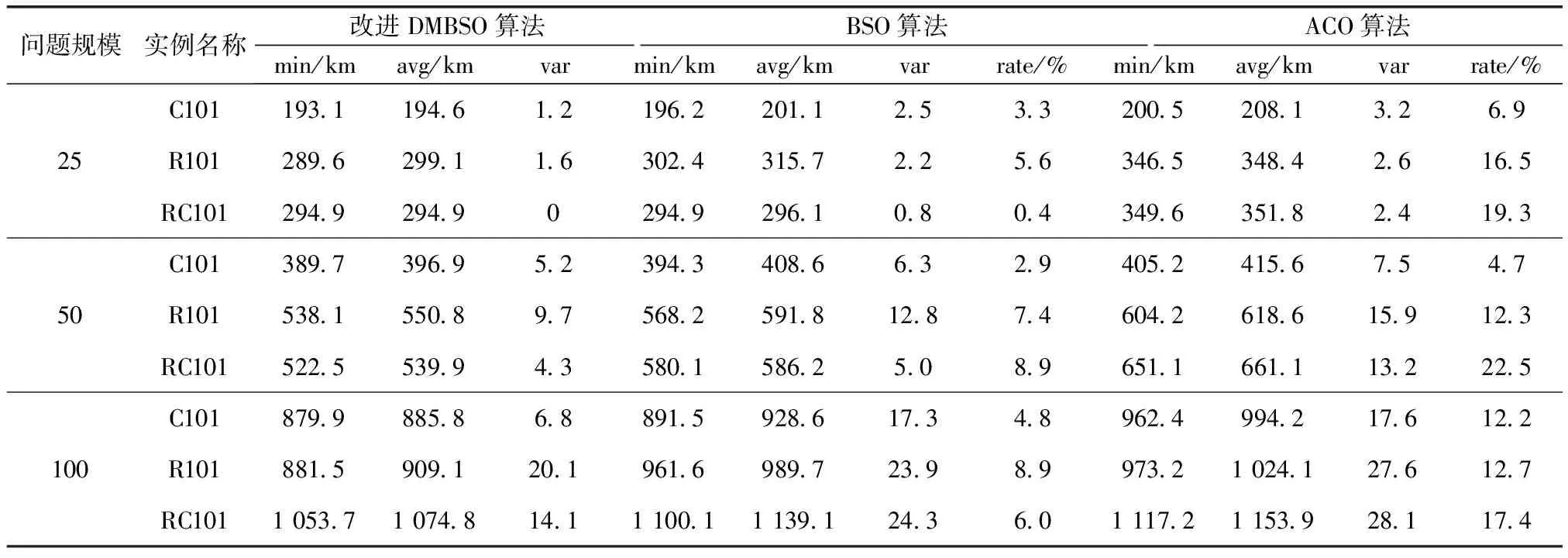
表2 三种算法求解结果比较

3.2 仿真分析算例

选取1个垃圾分拣中心和30个垃圾存放点进行模拟，将垃圾分拣中心标号为1，其他垃圾存放点顺次标号，分拣中心和存放点坐标以及垃圾产生量见表3。算法初始参数设置与3.1相同，设车辆行驶平均速度v=50 km/h，每升汽油的碳排放标准e0=2.32。

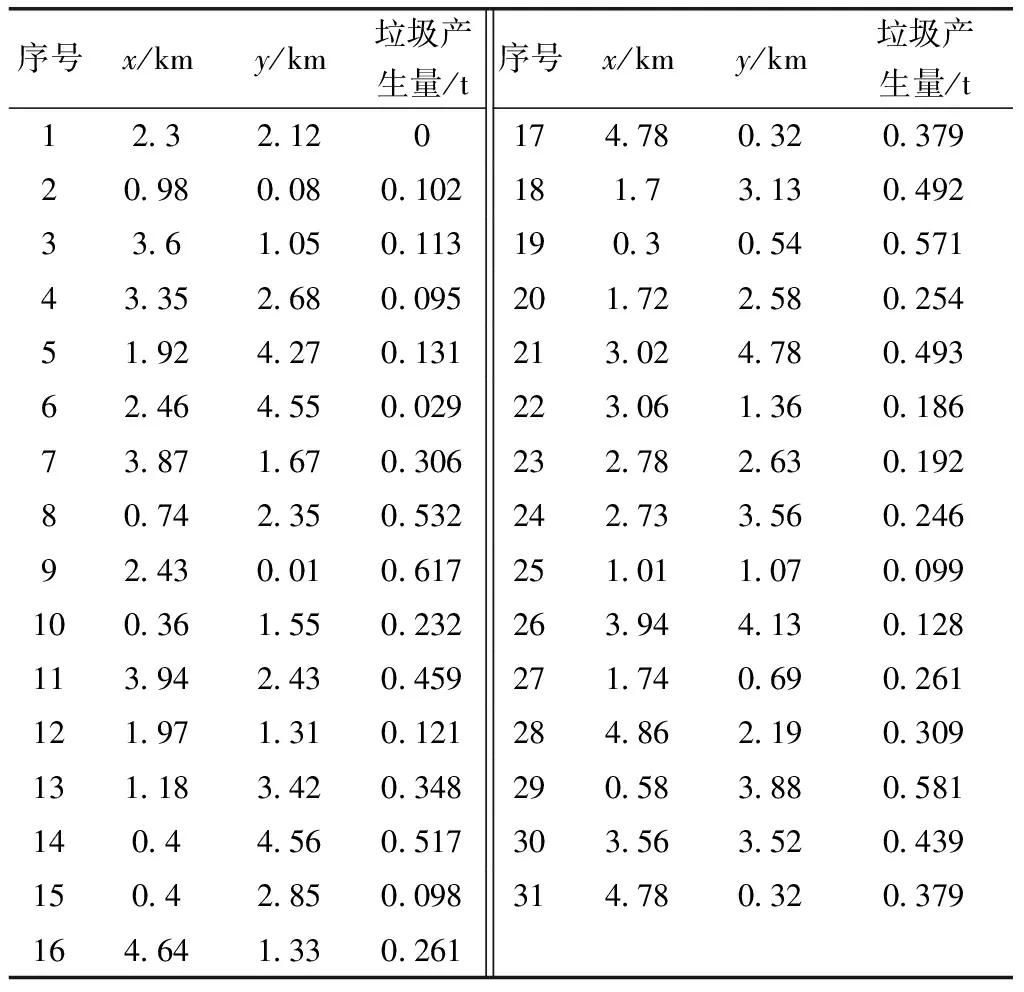
表3 节点位置及垃圾产生量

使用改进DMBSO算法对上述实例进行仿真，得到双目标下的垃圾收运最优路线如图3所示。为了验证改进DMBSO算法的性能，将其结果与BSO算法和ACO算法的求解结果进行对比，三种智能优化算法各迭代50次的优化过程如图4所示，可以看出蚁群算法可以得到较好的解，但并非最优解且不稳定，BSO算法求解较稳定，但是并未求得最优解，改进DMBSO算法求得最优解且收敛速度很快，收敛精度和收敛速度均优于另外两种算法。

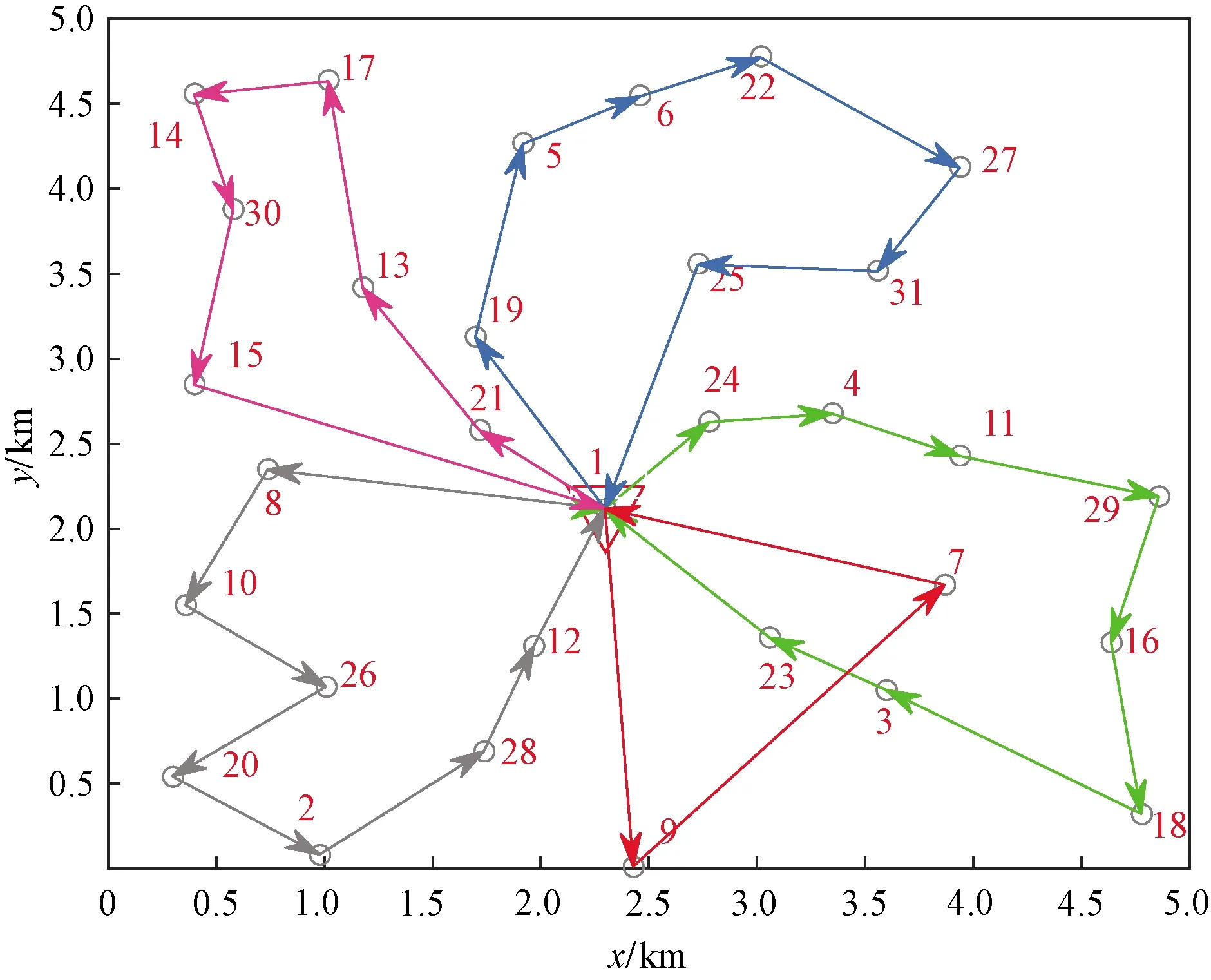
图3 最优路线轨迹图

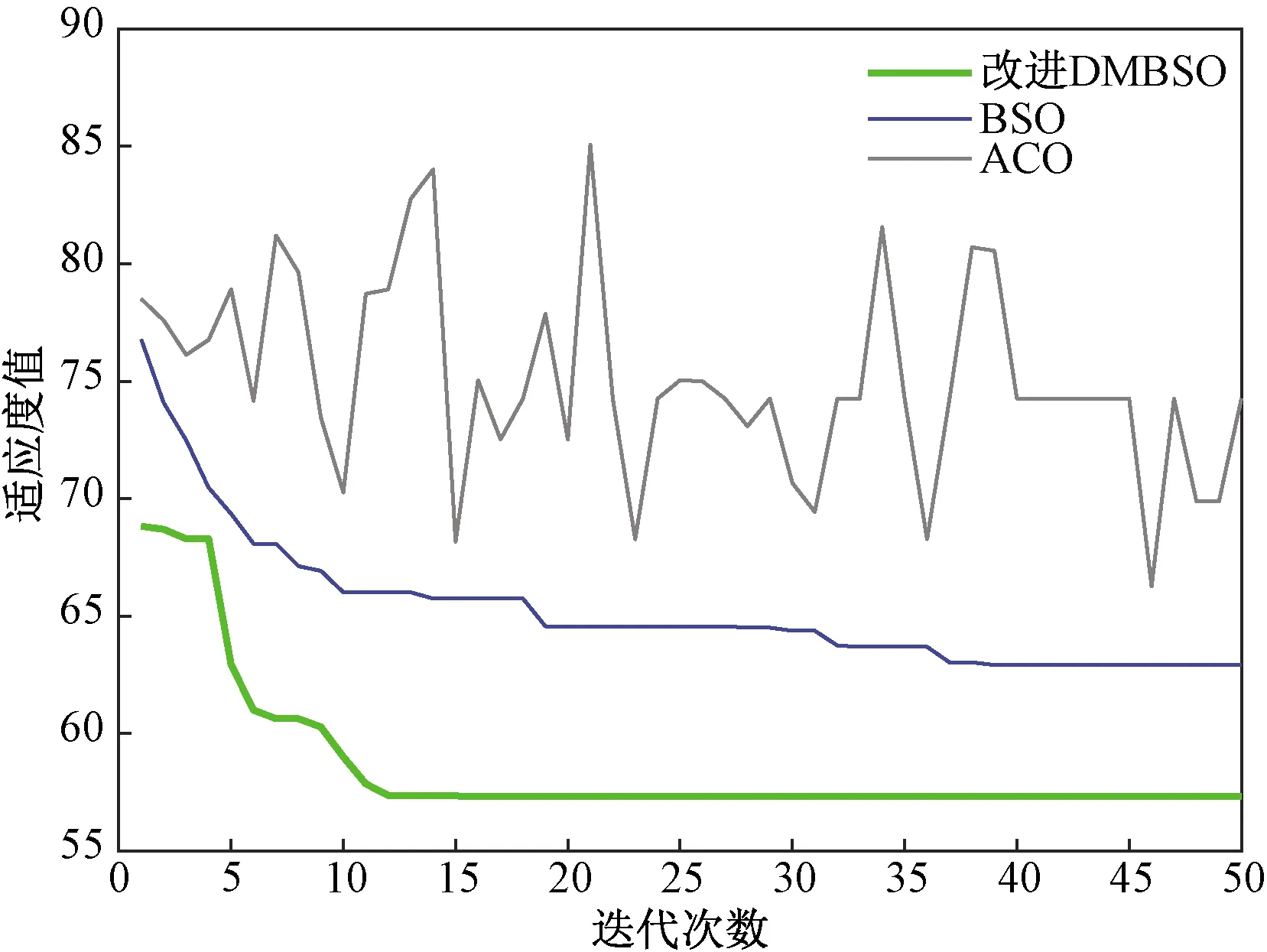
图4 三种智能优化算法优化过程

考虑到智能优化算法求解效果具有一定随机性，每次运行结果可能不一样，故每个算法均运行20次，更深层次比较三种算法的求解能力，运行结果如表4所示。

由表4可知，改进DMBSO算法在最优解和平均值方面均优于BSO算法和ACO算法，与3.1实验结论一致。在求解双目标时，改进DMBSO算法方差最小，且能够多次求得最优解，表现出更强的鲁棒性。另外，对求解结果实际意义分析，改进DMBSO算法比BSO算法和蚁群算法节省的距离分别为4.95%和14.95%，减少的碳排放量分别为15.38%和19.92%，故在多目标综合考虑情况下，改进DMBSO算法更有优越性。

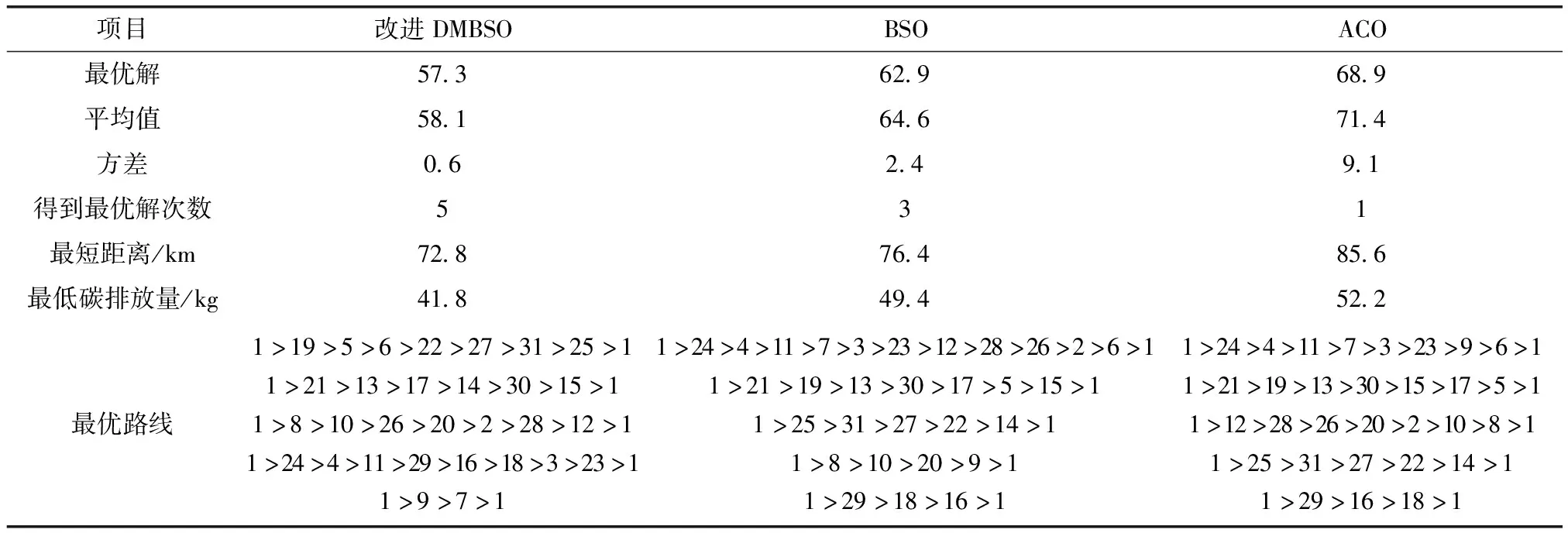
表4 三种智能优化算法求解结果比较

4 结论

随着全球环境的日益严峻和垃圾分类政策的出台，设计合理的垃圾收运路径是使用智能优化算法解决车辆路径优化(vehicle routing problem, VRP)新研究热点。在传统车辆路径优化的基础上，对垃圾收运路径进行分析，并考虑车辆载重对碳排放量的影响，建立了以最短距离和极小化碳排放量为目标的绿色垃圾收运路径优化模型。考虑车辆路径问题离散化的特点，对头脑风暴优化算法进行改进，引入启发式交叉算子、逆转算子和精英保留策略等优秀因子，设计出一种改进DMBSO算法，将其与BSO和ACO算法进行比较，仿真测试结果如下。

(1)在单目标情况下，改进DMBSO算法在搜索精度和鲁棒性方面均优于其他算法。

(2)在综合考虑最短路径和最低碳排放量双目标的情况下，改进DMBSO算法的求解效果更优，能够使两个目标同时达到最优且具有很强的稳定性。