燃气泄漏过程及爆炸对建筑构件损毁的数值模拟研究

吴静波，曾祥国*，杨 鑫，李 伟

(1.四川大学建筑与环境学院，深地科学与工程教育部重点实验室，成都 610065；2.成都理工大学环境与土木工程学院，地质灾害防治与地质环境保护国家重点实验室，成都 610059)

近年来，由于燃气泄漏引起爆炸事件屡屡发生，爆炸事故不仅会直接造成爆源附近的人员伤亡，而且会造成周围建筑物损伤破坏，甚至会导致建筑物因某些关键结构构件的失效而丧失承载平衡能力，致使结构发生局部或整体的连续倒塌。因此，燃气泄漏和扩散规律、燃气泄漏引起爆炸的条件(如燃气浓度、体积等)及其爆炸对建筑物损毁效应成为研究重点[1-4]。

目前，中外学者普遍单独研究燃气的泄漏过程或燃气爆炸，针对燃气泄漏后发生爆炸的两个过程的综合研究相对较少。现首先利用CFD软件对管道燃气泄漏到密闭空间和开放空间的规律进行模拟，接着根据泄漏时间和泄漏量对燃气进行TNT当量等效换算，最后采用AUTODYN软件对燃气在密闭空间爆炸对三种不同类型的墙壁损毁效应进行了对比。以期为燃气扩散后险情的控制、防护和救援提供依据。

1 管道燃气泄漏过程CFD模拟

1.1 基本控制方程

在ANSYS/CFD模拟燃气泄漏过程中，涉及的基本控制包括:连续性方程、动量方程、能量方程、组分方程和密度方程。

连续性方程:

(1)

式(1)中：ρ为流体密度；u为流体速度。

动量方程:

(2)

式(2)中：p为静压；τij为应力张量；gi和Fi分别为i方向上的重力体积力和外部体积力。

能量方程:

(3)

式(3)中:T表示流体温度；k为流体的湍流导热系数；σc为常数，一般取0.9～1；cpa为空气的定压比热；cpv为泄漏物质的定压比热；cp为混合物流体的定压比热，cp=ωcpv+(1-ω)cpa，ω为组分的质量分率。

组分方程:当求解涉及化学反应或者组分问题时，CFD通过求解组分的对流扩散方程来预测每个组分的局部质量分数，因研究的燃气泄漏扩散涉及化学组分，所以还需要组分方程的控制，由组分质量守恒定律可得气体扩散组分方程[25]为

(4)

式(4)中：Dt为泄漏扩散流体的质量扩散系数，Dt/D=(Sc/σc)μt/μ，σc是常数，一般情况为1；Sc为流体施密特数，Sc=μ/(ρD)。

密度方程:

(5)

式(5)中：R为普适气体常数；P是绝对压力；M为混合气体的平均分子量；Ma为空气的分子量；Mv为泄漏扩散物质的分子量。

1.2 天然气泄漏量的计算

管道泄漏模型分为小孔泄漏模型(泄漏点直径小于20 mm)、管道泄漏模型(管道完全断裂，泄漏孔面积为管道横截面积的80%～100%)和其他泄漏模型[26]。管道因为施工开挖而开裂时，泄露口通常介于小孔和完全断裂之间，综合小孔泄漏模型和管道模型来计算泄漏量较为准确，根据文献[27]知

(6)

式(6)中：一般对于燃气速度较小、管道较长的情况，取n=1，而对于燃气流速较大或者管道较短的情况，n=κ(κ为燃气的等熵指数)。如图1所示，p1为管道起始端压力，p2是泄漏点上游附近某点压力，qm,0为泄漏点上方管道内天然气质量流量，D是输气管道内径，λ是阻力系数，近似按城镇燃气设计规范提供的公式计算，L是泄漏点至管道起点的距离，取1 000 m。

图1 天然气管道泄漏示意图

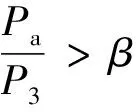
(7)

(8)

同时，作出假设

qm,0=qm

(9)

根据式(6)～式(9)，即可计算出泄漏量qm和泄漏处管内压力P3。表1为不同管径和泄漏孔径下天然气泄漏量计算结果。

表1 天然气泄漏量计算结果

1.3 计算模型

利用CFD 软件对燃气泄漏和扩散进行模拟分析，研究管道泄漏口附近泄漏扩散过程，分析计算域内天然气浓度变化规律和密闭空间压力随时间的变化规律。模拟考虑两种工况，工况1为燃气泄漏到密闭空间，工况2为燃气泄漏到开放空间，其示意图如图2所示。依据中国现有的城镇燃气设计标准GB 50028—2006，并结合现有的城镇燃气管网铺设概况，设燃气管道运行压力采用0.8 MPa，参考压力为标准大气压，管道直径为0.4 m，泄漏孔径为0.2 m，其泄漏的质量流量qm=15.875 kg/s。

图2 两种工况的简化计算模型

1.4 数值模拟结果与分析

甲烷的爆炸极限是5%～15%(体积分数)，因此主要分析天然气泄漏扩散过程中其浓度场的变化。

如图3所示，表示工况1不同时刻甲烷泄漏扩散的摩尔分数等值线图。在泄漏口处天然气的浓度最大，约为0.6。由于没有外界因素的影响，天然气泄漏扩散沿射流中心呈蘑菇状对称分布，在射流的中心线上天然气的浓度最大，两端逐渐降低。t=1 s时，从泄漏口向上至y=10 m，天然气主要向上扩散，y=10～18 m之间，由于天然气泄漏的初始速度的影响减小，蘑菇云迅速长大。t=2 s时，天然气向上扩散到26 m，主要由于天然气的密度比空气小，其在浮力作用下向上运动。当t≥8 s时，天然气扩散高度已经达到计算域的上限，由于计算模型壁面的限制，扩散方向会发生改变，天然气会沿着计算域的边界向中心扩散，直至充满整个计算域。

图3 工况1不同时刻甲烷摩尔分数分布

图4表示工况2不同时刻摩尔分数等值线，在t≤4 s时，天然气的扩散形式和图4结果类似，但其扩散速度较快。当扩散高度超过计算域时，计算域中只能显示底部射流部分。

图5表示监测点位置，其中监测点1位于泄漏口正上方1 m，对应图6(a)黑色曲线。在扩散初期，甲烷的浓度先是急剧增大，达到0.63左右，然后快速下降，接着小幅度上升后趋于水平，同时可以看出其他四个点的浓度随时间变化的趋势与监测点1类似；监测点2和5处于同一高度，它们浓度变化起始时间十分接近，但是监测点2浓度曲线增加到0.4后就基本趋于水平，而监测点5浓度增加到0.27后却迅速下降到0.1，其原因为监测点2位于泄漏口的正上方，天然气射流中心线附近流场比较稳定，天然气扩散到5 m(即监测点2的高度)时，该监测点浓度快速上升然后趋于不变；泄漏扩散刚发生不久，监测点5所处位置的流场变化较大，以致其浓度变化范围很大，当该区域流场趋于稳定后，其变化就不再明显。

图5 监测点位置

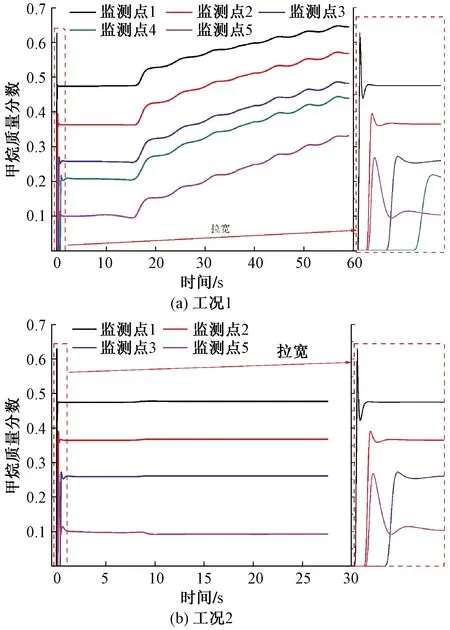
图6 工况1与工况2监测点甲烷质量分数随时间的变化曲线

结合图6，可以发现两种工况在0～15 s内甲烷浓度曲线变化趋势是类似的，随后工况1甲烷浓度由于空间的限制会缓慢地上升，而工况2因为扩散到开放空间，天然气能够自由流动，所以监测点的浓度曲线变化不明显。

上述分析仅通过某些监测点的质量分数来描述天然气泄漏的状态，但不足以反映整个流场甲烷浓度随时间的变化情况。图7为工况1甲烷质量和摩尔分数随时间的变化曲线，可知在10 s前，两条曲线的增长速率是比较缓慢的，随后以较大的斜率增加；甲烷摩尔分数比质量分数大，且两条曲线基本上呈线性增长，这与实际情况相符。图8为工况1计算域内平均压力(相对标准大气压而言)随甲烷泄漏时间的变化规律，随着甲烷扩散的进行，其先快速地增加，并在60 s后逐渐稳定。通过拟合，可知平均压力随时间呈现3次多项式变化趋势。

图7 工况1甲烷质量和摩尔分数随时间的变化曲线

图7和图8中的曲线分别充分地反映了泄漏后流场内甲烷浓度和压力的变化，这对实时了解天然气的浓度分布和泄漏域内压力大小，以及泄漏扩散后险情的控制、防护和救援具有重要科学意义。

图8 工况1空间内平均压力随时间的变化曲线

2 燃气爆炸对墙壁损毁的数值模拟

2.1 TNT当量计算

关于可燃气体与TNT当量法之间换算与适用性可参考文献[14]。

甲烷/空气混合气体的爆炸化学反应方程式为

(10)

氧气在空气中的体积浓度为21%，1 mol甲烷在空气中完全反应的化学方程式为

(11)

根据盖斯定律，参考表2甲烷/空气混合气体反应生成焓，可以求出1 mol乙炔在空气中反应的爆热为Qv，则单位质量的甲烷/空气混合气体爆炸产生的爆热Qm为

表2 甲烷/空气混合气体及爆炸产物生成焓

(12)

甲烷泄漏质量为

Mm=qmt

(13)

式(13)中：Mm为甲烷泄漏质量；qm为甲烷泄漏的质量流量，取15.875 kg/s；t为泄漏时间，21.7 s。

等效TNT质量为

(14)

式(14)中：MTNT为等效TNT质量；α为TNT当量效率，取0.04；Qm为甲烷/空气混合气体的爆热；QTNT为TNT的爆热，取4.52 MJ/kg。

根据式(12)～式(14)，计算获得:Qm=3 283.55 KJ/kg，Mm=344.49 kg，MTNT=10 kg。

2.2 爆炸对墙壁损毁的数值模拟结果与探讨

选择1.3工况1(密闭空间)作为模拟背景，以砖墙、钢筋混凝土墙和混凝土墙作为密闭空间不同种类的墙壁。数值模拟采用Autodyn软件，计算中涉及的材料包括:空气、TNT、混凝土、钢筋、砖和砂浆，各材料模型见表3。

表3 材料模型

考虑到计算量的大小，数值模拟过程中选择4 m×1.8 m×0.1 m作为墙壁计算模型，图9为1/2模型。钢筋与混凝土采用分离式建模，以共节点方式耦合，边缘钢筋距混凝土模型上下距离为0.2 m、右侧为0.4 m，钢筋网间距为0.2 m×0.2 m，横截面积7.85×10-4m2；砖块尺寸为0.225 m×0.075 m×0.1 m。固定墙壁最下端，覆盖墙壁的空气采用Flow-out边界条件；计算时间为10 ms。以1/2模型左下角为原点，点1坐标(x，y，z)=(0.4，0.2，0)和点7坐标(x，y，z)=(0，0.6，0)，相邻点间距0.2 m，所有观察点均位于墙壁的迎爆面上且三种墙壁的观察点分布一致。此外，参考根据1.4节工况1模拟结果，选取爆源中心到墙壁距离为0.5 m。为避免计算时间过多地消耗在流体单元，实现远场爆炸，基于Autodyn的remap技术，将一维计算结果映射到三维计算模拟中，其映射部位在左下角正前方。

图9 砖墙和钢筋混凝土墙模型及观察点分布

图10表示三种类型墙壁爆炸后的效果。可以看出，三种类型墙壁均在其下端中心部位产生凹陷变形或破坏，这是因爆炸冲击作用向外扩展造成的。图10(a)中砖墙中下部因爆炸强冲击作用而产生方形断口，其面积约为0.076 m2，最下方砖块也产生一条破坏带，破坏长度为1.2 m。图10(b)和图10(c)分别表示钢筋混凝土墙和混凝土墙的损伤情况，两墙壁破坏部位基本相似，墙壁上侧和左右侧产生多条层裂损伤，这是反射拉伸应力波在自由面附近造成的。同时两墙壁都在底部位产生两条破坏带，前者最底部位和最底偏上部位破坏带长度分别约为1.09 m和0.56 m，后者最底部位和最底偏上部位破坏带长度分别约为1.05 m和0.2 m。

图10 三种类型墙爆后效果

如图11(a)～图11(c)，表示三种墙壁压力在1 ms内的曲线。可以看出，砖墙受到的爆炸压力衰减速度快于钢筋混凝土墙和混凝土墙所受到的压力，后两者压力出现明显的负压，且后期压力震荡性较大。图11(d)中以观察点Gauge#1和#7分别作为水平和竖直方向上观察点的x轴坐标起点(下同)，表示各观察点压力峰值随距离变化的曲线。除砖墙观察点Gauge#7～12压力峰值随距离变化表现波动外，其余各观察点压力峰值随距离增大而下降。爆炸应力波正向接触墙壁后，墙内压缩应力波便向四周传播，并随传播距离而发生能量衰减，由于应力波在墙壁的竖向先于水平发生反射，并与压缩应力波发生叠加，从而降低墙壁竖向压力峰值。故三种墙壁水平观察点Gauge#1～6的压力峰值多大于竖向观察点Gauge#7～12的压力峰值。该现象在距离为0～0.6 m范围内表现明显，而距离为0.6～1 m范围横竖向压力峰值较接近。图11(e)为压力峰值随距离变化的拟合曲线。除砖墙观察点Gauge#7～12之外，其余观察点都表现为指数衰减趋势，且水平观察点压力峰值衰减幅度大于竖向观察点。在相同距离下，砖墙横竖向压力峰值的差值大于其余两种墙壁，钢筋混凝土墙横竖向压力峰值的差值最小。

图11 压力时程曲线与压力峰值和距离的关系

如图12(a)～图12(c)，表示三种墙壁速度时程曲线。由于受到压缩应力波冲击作用，墙壁压力陡然上升，造成墙壁质点速度也迅速增大到峰值，可知0～1 ms内加速度值很大；随着时间增加，墙壁受力必然下降，而后期的速度达到峰值后却是缓慢下降，几乎是呈直线下降趋势，表明加速度变化很小。此外，还可看出砖墙的观察点速度大于钢筋混凝土墙和混凝土墙上对应的观察点速度。在图12(d)中，随着距离增大，三种墙壁观察点的速度峰值都快速下降；相同距离下砖墙的观察点速度峰值都大于钢筋混凝土墙和混凝土墙的观察点速度峰值，而后两者的速度峰值较接近。相比钢筋混凝土墙与混凝土墙，砖和砂浆的动态抗压强度都较小，且砂浆更容易受到破坏而丧失抵抗能力，造成砖墙抗爆炸压力较弱，墙壁速度较大而更易破坏。图12(e)为砖墙和钢筋混凝土墙的观察点速度峰值的拟合曲线。由于钢筋混凝土墙和混凝土墙的观察点速度峰值接近且变化趋势一致，因此采用钢筋混凝土墙观察点速度峰值拟合曲线代替后者的拟合曲线。通过对砖墙和钢筋混凝土墙的水平与竖直观察点的速度峰值拟合，发现这两类墙壁观察点速度峰呈现指数衰减趋势，且砖墙观察点速度峰值衰减幅度更大。

图12 速度时程曲线与速度峰值和距离的关系

如图13(a)～图13(c)表示三种墙壁测点位移时程曲线。可以看出，越靠近爆源，位移越大；对砖墙而言，Gauge#7的位移从墙壁产生位移开始就大于Gauge#1的位移，而钢筋混凝土墙和混凝土墙则大约在2.5 ms后Gauge#7的位移才大于Gauge#1的位移。图13(d)为砖墙和钢筋混凝土墙Gauge#7的位移时程曲线，从爆炸应力波加载墙壁开始，砖墙的Gauge#7的位移就明显大于钢筋混凝土墙的Gauge#7的位移，这是因砖墙抗压强度较小，更易于发生变形和破坏。通过拟合，发现两种墙壁相同位置观察点都呈线性关系。

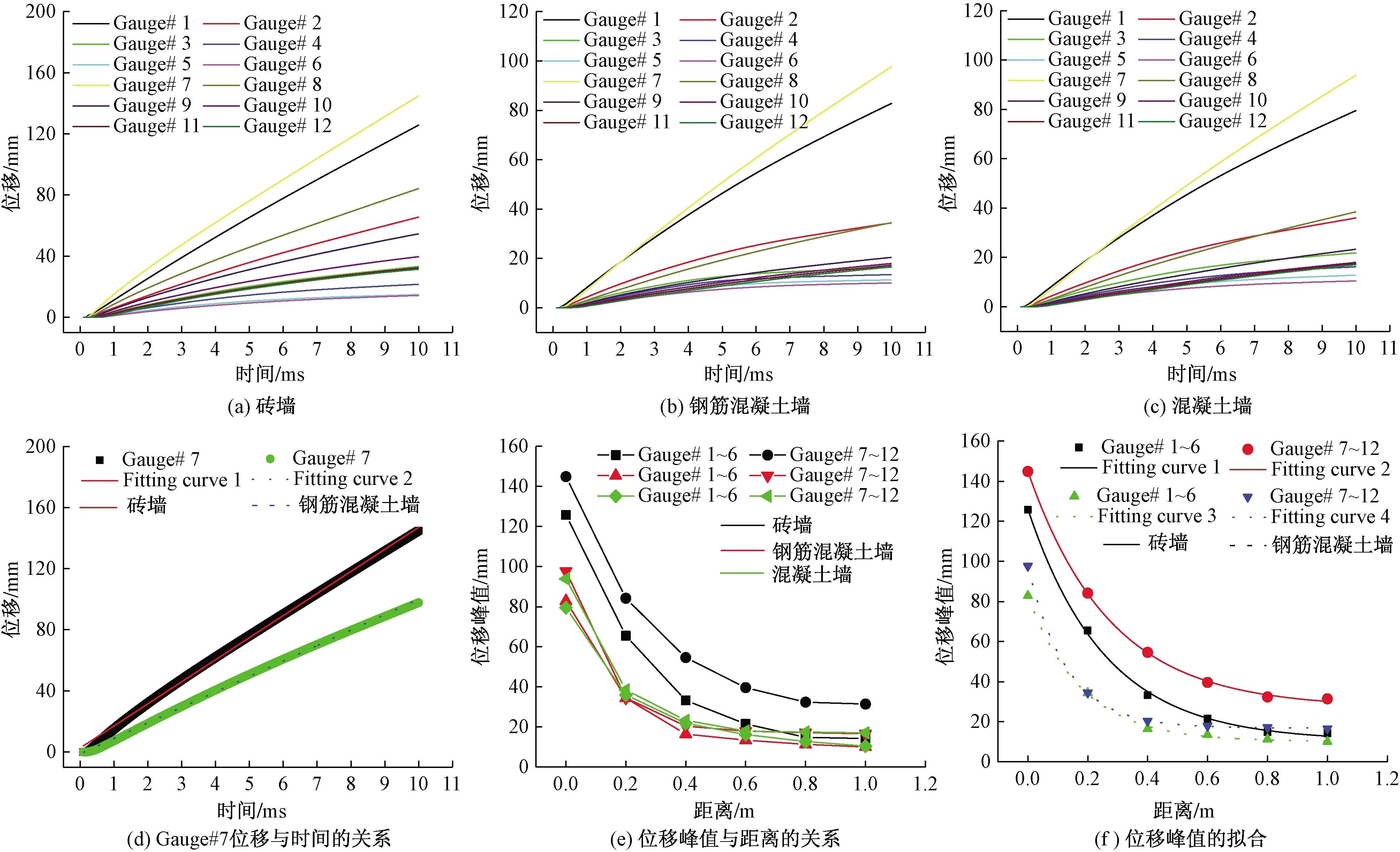
图13 位移时程曲线与位移峰值和距离的关系

图13(e)为位移峰值与距离的关系。三种墙壁竖直观察点Gauge#7～12的位移峰值基本上都大于水平观察点Gauge#1～6，且相同距离下砖墙的竖直观察点与水平观察点位移峰值的差值大于其余两种墙壁的差值。由于墙壁下端固定，爆炸应力波正面作用墙壁，使墙壁朝后发生变形，而墙壁两侧因下端固定而变形相对较小，因此墙壁竖直观测点位移大于水平观测点位移。图13(f)表示位移峰值拟合曲线，这两类墙壁观察点位移峰同样呈现指数衰减趋势。

3 结论

(1)对比燃气泄漏到密闭空间与开放空间两种工况的浓度分布图，发现前者扩散速率慢于后者，主要由于密闭空间的限制降低了甲烷和空气的对流扩散速率。

(2)两种工况在扩散时间为0～15 s内，甲烷质量分数变化曲线基本一致；扩散时间超过15 s后，密闭空间的甲烷质量分数会继续增大，而开放空间的甲烷质量分数则保持基本不变，这表明甲烷泄漏扩散时间对其质量分数有重要影响。

(3)三种墙壁观察点压力峰值、速度峰值、位移峰值基本上随距离增大而表现为指数衰减趋势。砖墙水平压力峰值基本上大于竖直压力峰值，水平速度峰值、位移峰值却分别小于竖直速度峰值、位移峰值；钢筋混凝土墙和混凝土墙皆表现为水平压力峰值、位移峰值小于竖直压力峰值、位移峰值，水平速度峰值大于竖直速度峰值。

(4)通过CFD计算获得了甲烷平均浓度和压力随时间变化规律，同时运用Autodyn模拟燃气爆炸对密闭空间墙壁损毁效应，两者共同为甲烷泄漏扩散后险情的控制、防护、救援以及对建筑物损毁的检测、评估提供了科学依据。