一种基于两级阈值的像素不扩展视觉密码方案*
孙 瑞, 付正欣, 李小鹏, 郁 滨
信息工程大学, 郑州450001
1 引言
Naor 和Shamir[1]将秘密共享的思想运用到了数字图像领域,形成了视觉密码(visual cryptography,VC) 这一研究热点. 有别于传统密码学大量繁复的解密运算, 视觉密码的主要特点在于无条件安全性和重建图像简单性. 对于特定参与者集合, 不需要任何复杂运算, 通过人类视觉系统(human visual system,HVS) 即可重建秘密图像, 而剩余参与者集合则无法获取秘密图像的任何内容. 视觉密码方案设计主要围绕降低像素扩展度、提升恢复质量和保证安全性等三个方面展开. 像素不扩展视觉密码是在保证视觉密码严格安全性的前提下, 利用随机栅格、概率法、多像素加密法等像素不扩展分享方法, 结合数字图像处理技术, 平衡恢复质量和图像尺寸的固有矛盾, 实现恢复图像质量提升的目标.
Kafri[2]等人以函数运算为基础, 提出了(2,2) 门限结构随机栅格(random grid, RG) 方案, 利用随机化fran、相等fequ和取反fcom三个函数实现了秘密信息分享. 在此基础上, Shyu[3]设计了(n,n) 门限结构和灰度/彩色空间下的随机栅格方案, Chen 等人[4]将随机栅格存取结构扩展到的(k,n) 门限结构,Wu 等人[5]通过定义彩色像素“异或” 运算, 生成通用存取结构下彩色共享份. 在恢复质量提高方面, Wu等人[6]设计了更一般化的随机栅格方案, 通过调整首张共享份黑白占比, 提高恢复图像对比度, Hou 等人[7]设计了逼近对比度理论极限的(2,n) 门限随机栅格方案, Hu 等人[8]通过排布像素位置, 提高了门限方案的对比度.
Ito 等人[9]以确定型方案基矩阵作为分享矩阵, 随机选取分享矩阵一列分享, 实现了恢复图像尺寸不扩展. 在此基础上, Yang[10]提出并正式定义了概率型视觉密码(probabilistic VC, PVC), 构建了不依赖于确定型视觉密码基矩阵的(2,n)、(n,n) 和(k,n) 门限结构分享矩阵. Hou 等人[11]利用基矩阵构建分享矩阵, 设计了共享份质量提升的渐进式视觉密码方案, 然而恢复质量并未得到改善. Wu 等人[12]以彩色共享份替代黑白共享份实现了共享份尺寸不扩展. 随机栅格法的恢复效果与概率法相似, Yang 等人[13]证明了随机栅格法与概率法的等效性. 虽然随机栅格法与概率法的恢复图像被逐步优化, 但由于秘密图像中每个像素被独立处理, 没有考虑像素邻域特征关联关系, 导致恢复图像中少数像素分布不均匀, 恢复效果较差.
多像素加密视觉密码(multi-pixel encryption VC, MEVC) 方案以多个像素为基本处理单元, 将包含一定数量的秘密像素块作为加密对象, 映射到共享份中相同数量的像素, 从而实现像素不扩展. Hou 等人[14]首先提出了多像素分享思路, 以确定型方案基矩阵为分享矩阵, 每次分享固定数量的像素, 依据像素块中黑色像素占比选择相应加密矩阵. 基于相同条件, 多像素法恢复图像的全局对比度与概率型全局对比度相同, 但黑白像素分布更加均匀, 视觉效果更优. 为了反映上述差别, Hou 等人[15]引入方差反映局部图像的平滑程度, 与相对差一同作为恢复图像效果的评价指标. 方案[14] 分享算法在选择基矩阵时随机性不强, 恢复图像出现周期性的条纹. Liu 等人[16]优化了上述算法, 任一像素块都以一定的概率选择基矩阵, 消除了恢复图像中的纹理. 张等人[17]提出了行扫描、列扫描、Zigzag 扫描等三种扫描方式的多像素编码方案, 然而恢复质量提升有限.
为了提升多像素加密视觉密码方案的恢复图像质量, Chen 等人[18]提出了多灰度级基矩阵构建方法,灰度图像中平均灰度级高的块映射到恢复图像中块的平均灰度值也相应高, 由于不仅只有两级灰度, 恢复图像的表现力更强. Lee 等人[19]通过灰度秘密图像的直方图特征, 选取不同的映射关系, 间接实现了直方图均衡化, 改善了恢复图像的显示效果. Yan 等人[20]面向灰度图像, 采用融合了误差扩散法与视觉密码的AbS 架构, 将恢复图像与秘密图像之间的误差扩散至高频带, 生成了具有蓝噪声特征的恢复图像.Sun[21]等人提出基于快速直接二值搜索算法的像素不扩展视觉密码方案, 将概率型视觉密码分享算法嵌套于半色调寻优过程中, 以共享份叠加结果为优化对象, 最终实现寻优策略下的最优恢复图像, 视觉质量得到进一步提升. 上述几种方案仅适用于(n,n) 门限结构.
已有的像素不扩展视觉密码方案中, 较优的恢复质量往往受限于(n,n) 门限结构, 且以复杂设计方案和高计算复杂度为代价, 而面向一般(k,n) 存取结构的方案, 处理细节内容的能力不足, 秘密图像中细节内容恢复不佳. 像素不扩展视觉密码中, 秘密像素只能以一定概率被恢复, 恢复概率与分享算法密切相关.多像素概率型视觉密码方案设计的关键, 是确定秘密像素块灰度集合到分享矩阵的映射关系, 通过调节映射关系可以强调图像特定内容.
据此, 本文提出了一种面向一般(k,n) 存取结构的多像素加密视觉密码方案. 方案从图像的空域出发,依据秘密像素块黑色像素密度, 采取块尺寸由大到小调整、分类处理的方法, 以一级阈值区分秘密图像中低频和高频区域, 进而采取不同的分享方法, 低频区域作为纯色像素块分享, 以二级阈值调控高频区域中单位块灰度与分享矩阵的映射关系, 达到了增强恢复图像中部分细节表现的效果. 理论证明本方案具有与确定型视觉密码方案同等强度的安全性, 实验结果和对比分析证明了方案的有效性.
2 基本概念
多像素加密方案一次分享若干个秘密像素, 已有的确定型视觉密码定义和概率型视觉密码定义无法涵盖多像素加密方案, 本节给出了多像素加密视觉密码的定义, 介绍了两种典型的像素不扩展视觉密码实现方案.
2.1 多像素加密视觉密码定义
多像素加密视觉密码分享一幅二值秘密图像G产生n个共享份Si ∈ZM×N2(i ∈[1,n]), 并将n个共享份打印至透明胶片后分发给n个参与者, 只有特定组合的参与者即授权子集, 才能通过叠加共享份解密出视觉系统可直接识别的信息, 而对其他组合的参与者即禁止子集, 不能恢复出任何信息, 对(k,n) 方案,授权子集为参与者数量大于等于k的所有可能组合的集合.
定义1 一个(k,n)-MEVC 方案由基矩阵B1,B2,··· ,Bt组成, 秘密图像和恢复图像的块灰度集合分别为D和E. 秘密图像G中包含相同数量像素的任意两个不重叠区域坐标索引集合Ω1和Ω2,不失一般性地, 设H(G[Ω1])>H(G[Ω2]),H表示平均灰度. 分享秘密图像G生成n幅共享份Si ∈ZM×N2(i ∈[1,n]). 设d为参与者个数, 参与者集合P={i1,i2,··· ,id} ⊆ {1,2,··· ,n},E={e:e=H(η(Bi〚P〛))}(i= 1,2,··· ,t),η(B〚P〛) 表示限制矩阵B行数至集合P得到新矩阵的行向叠加结果. 如果满足以下两个条件, 则秘密分享算法可称为有效的(k,n)-MEVC.
(1) 对比性条件. 当d ≥k时,
对于实验设定如下评判标准:(1)注重荷载-沉降曲线观察,确定承载力陡降的同时,查看位移传感器的显示数据,确认总沉降量是否大于40mm;(2)基础桩因受承载过大已经发生破坏,且破坏仍在不断增加;(3)针对桩长超过25m的基础桩,其荷载-沉降曲线缓慢变形的阶段尚未出现;(4)实验中,若发生下一次的沉降量是本次沉降量的2倍且此状态还在持续,则表明基础桩荷载受力还未稳定;(5)实验中加载的最大荷载大于设计单桩承载力的2倍是实验数据有效的基础,若施加荷载不够,则实验无效。

满足H(R1)≥H(R2), 符号V表示矩阵行向叠加运算.
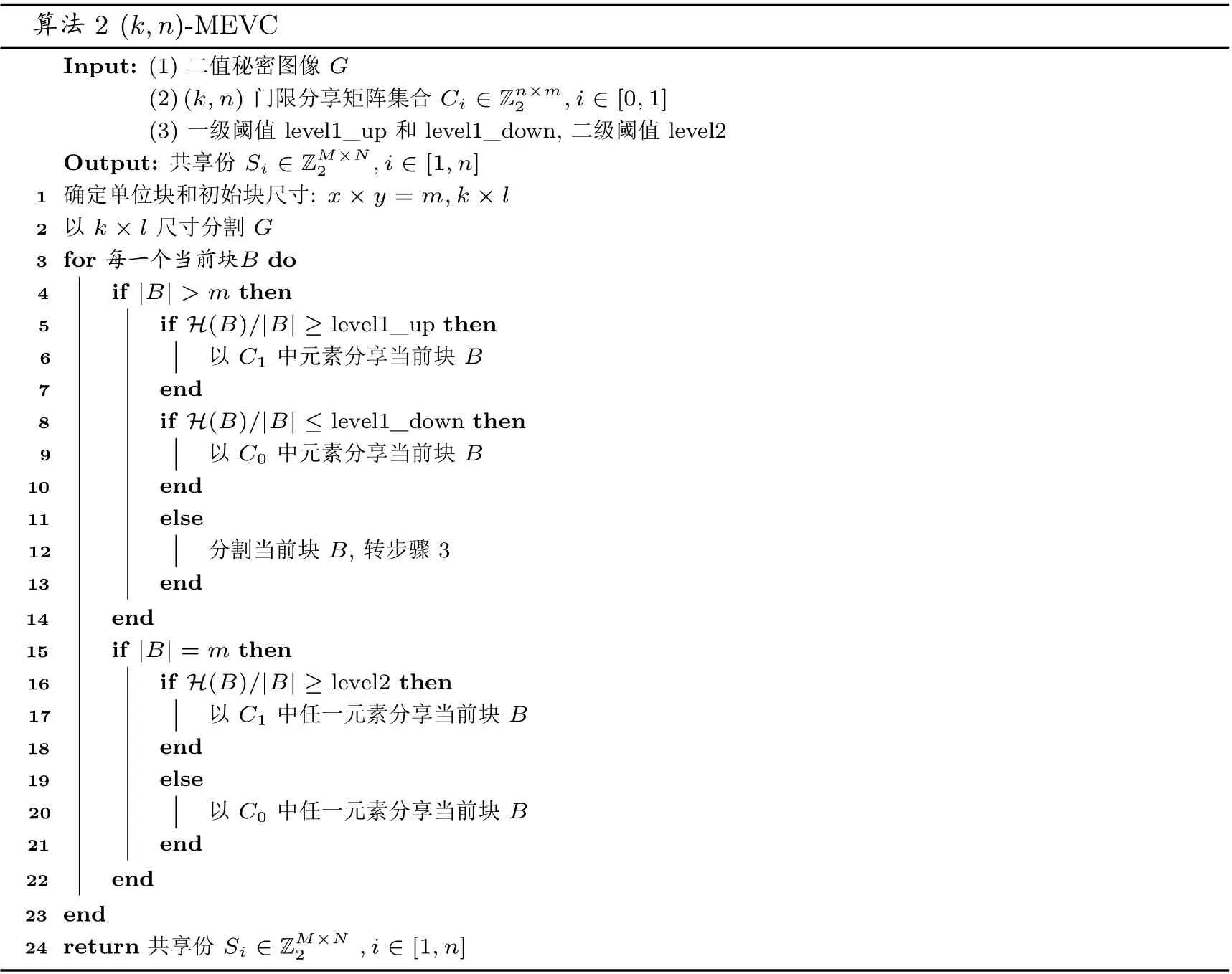
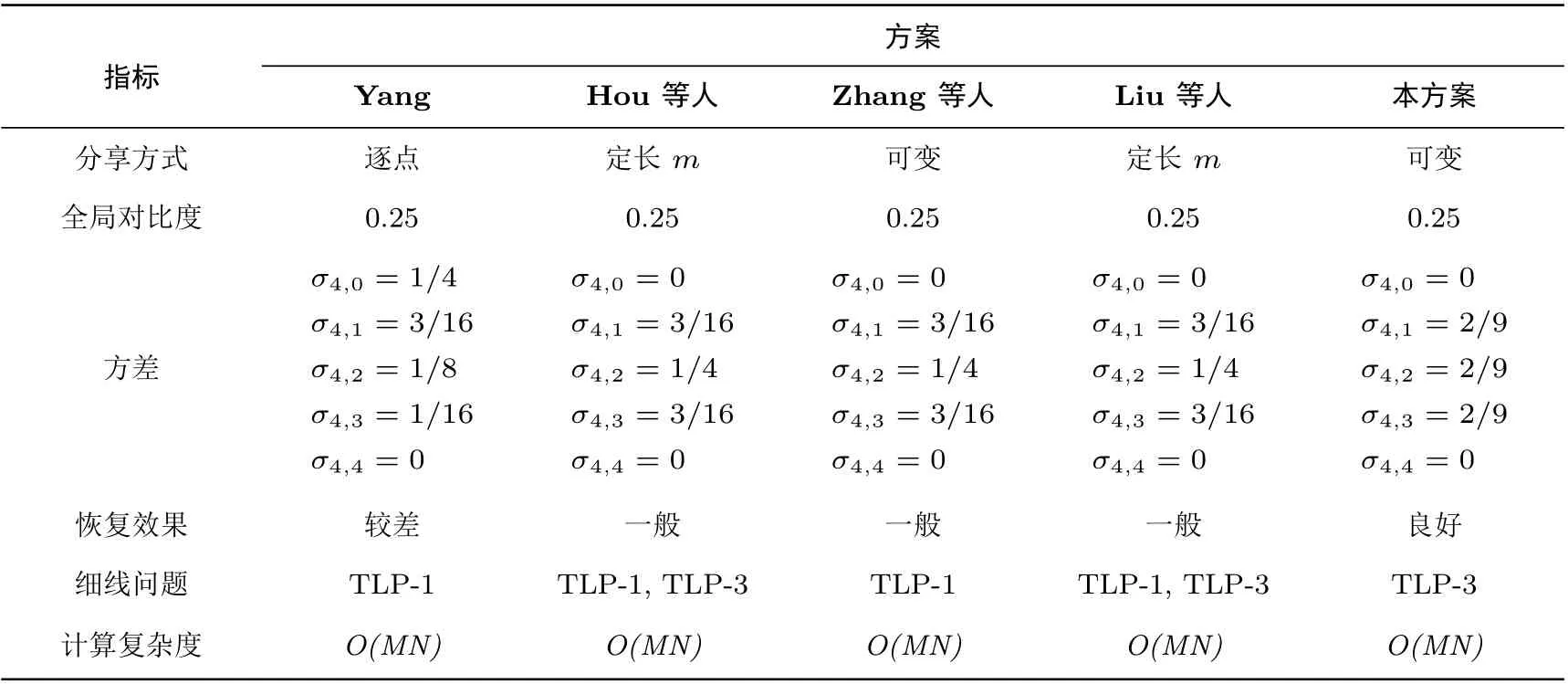
(2) 安全性条件. 当d 满足f1~f2, 即f1和f2有相同的矩阵集合和概率分布, 给定矩阵fℓ, 无法从中获知秘密图像G的任何信息, Pr{Gℓ=g}=Pr{Gℓ=g|fℓ}, g ∈D. 第一个条件保证参与者人数为不少于k个时, 秘密图像能被正确恢复出来, 第二个条件保证参与者人数小于k时, 共享份叠加所得的图像不会泄露秘密图像的任何信息, 即使敌手具备无限计算资源和运算时间, 也无法得到有关秘密图像的确定信息. Liu 等人[16](k,n)-MEVC: 设(k,n) 确定型视觉密码的基矩阵为n×m的B0和B1,C0=〈B0〉,C1=〈B1〉, (〈A〉表示矩阵A 的列向全排列组成的矩阵集合). Liu 等人以像素数量m的块为单位分享秘密图像, 单位块中含有的黑色像素数量表示为b, 像素块选择分享矩阵的规则如算法1: 算法1 1. E[b] ←b, b = 1,2,··· ,m 2. N [b] ←m, b = 1,2,··· ,m 3. 若Random(N[b]) < E[b]4. 随机选取C1 中任一矩阵填至共享份相应位置5. E[b] ←E[b]−1 6. N [b] ←N [b]−1 7. 否则8. 随机选取C0 中任一矩阵填至共享份相应位置9. N [b] ←N [b]−1 10. 若N [b] = 0,E[b] ←b,N [b] ←m 该方案采取了块分类处理的思想, 对每一类块, 分别设立记录已分享次数的计数器E[b] 和N[b]. 对于含有b个黑色像素的块, 以b⁄m概率选择矩阵集合C1中元素加以分享, 以(m −b)/m概率选择矩阵集合C0中元素加以分享, 方案的对比性条件和安全性条件由确定型视觉密码的基矩阵保证. 本节针对之前方案处理细节内容能力不足和恢复效果较差的问题, 提出了基于两级阈值的多像素加密分享算法, 并就算法的有效性进行了理论证明. 方案流程如图1, 在分享秘密图像时, 首先以初始尺寸分割秘密图像, 当检测到当前块黑色像素密度大于等于上阈值时, 将此块作为黑色块处理; 当检测到当前块黑色像素密度小于等于下阈值时, 将此块作为白色块处理; 当前块灰度密度介于上阈值和下阈值之间时, 继续分割并分享, 直至当前块尺寸与单位块尺寸相同且不满足上阈值和下阈值, 不再继续分割, 以二级阈值选择基矩阵. 通过设定二级阈值取值, 进而调控分享矩阵选择, 当意图突出白色细节时, 阈值设置应大于0.5; 当意图突出黑色细节时, 阈值设置应不大于0.5. 二级阈值与0.5 的偏离程度决定了强化效果, 偏离程度越大, 强化效果越明显. 方案伪代码表述如算法2. 图1 方案流程图Figure 1 Block diagram of proposed scheme 算法2 (k,n)-MEVC Input: (1) 二值秘密图像G(2)(k,n) 门限分享矩阵集合Ci ∈Zn×m2 ,i ∈[0,1](3) 一级阈值level1_up 和level1_down, 二级阈值level2 Output: 共享份Si ∈ZM×N2 ,i ∈[1,n]1 确定单位块和初始块尺寸: x×y = m,k×l 2 以k×l 尺寸分割G 3 for 每一个当前块B do 5 if H(B)/|B| ≥level1_up then 4 if |B| > m then 6以C1 中元素分享当前块B 7 end 8 if H(B)/|B| ≤level1_down then以C0 中元素分享当前块B 10 end 11 else 9 12 分割当前块B, 转步骤3 13 end 14 end 15 if |B| = m then 16 if H(B)/|B| ≥level2 then 17 以C1 中任一元素分享当前块B 18 end 19 else 20 以C0 中任一元素分享当前块B 21 end 22 end 23 end 24 return 共享份Si ∈ZM×N2 ,i ∈[1,n] 在分享算法中, 以单位块作为共享份填充的基本单元. 首先依据基矩阵列长m确定x和y, 使得单位块的纵横比尽可能接近1, 最大程度接近正方形. 若无法满足纵横比要求, 可对基矩阵列作适当填充. 进一步确定初始块的尺寸k和l, 使其长宽满足单位块长宽的整数倍. 每次分享的秘密像素块是若干满足阈值条件的像素, 且像素块尺寸为单位块尺寸的整数倍. 设|B| 代表秘密像素块B包含的像素数量, 单位块包含的像素数量为m, 可将秘密像素块划分为|B|/m个单位块,对每个单位块而言, 都由C0或C1中任意一个矩阵分享. 定理1 (k,n)-MEVC 算法满足视觉密码的对比性条件. 秘密分享的整个过程由若干单位块分享构成, 算法的有效性建立在基矩阵的选取和基矩阵随机重排上, 与分割方式和填充方式无关. 另外, 对单位块而言, 填充方式的改变, 并不影响其对比性条件和安全性条件. 本方案的有效性与Naor-Shamir 视觉密码方案的有效性是等价的. 本节通过实验验证算法的有效性. 对比文献选择应面向同一类分享对象、解决同一问题. 本文的目的是提升恢复图像的视觉质量, 而非共享份的视觉效果, 因此排除扩展型视觉密码; 面向一般的(k,n) 门限结构, 排除只面向(n,n) 结构的分享方案. 同时本方案符合无条件安全性, 排除降低安全性条件从而提升视觉效果的设计方案. 基于以上考虑, 选取了Yang[10]、Hou 等人[14]、Liu 等人[16]的方案, 针对6 个指标作对比分析. 为了证明本文方案的有效性, 给出了(3,3) 门限结构下分享图像的实验结果, 基矩阵为: 秘密图像为一幅尺寸为384×384 的Lena 二值图像, 参数设置如下: 单位块尺寸2×2 像素、初始块32×32 像素、上阈值0.95、下阈值0.1、二级阈值0.5. 如图2, (3,3) 门限结构下恢复图像对比度下降为秘密图像的1/4, 图(b) 所示为图(a) 对比度下降1/4 所得图像. 图(c)(d) 和(e) 为分享秘密图像(a) 生成的3 幅共享份, 任意一张共享份均为类噪声图像,视觉上无法从中获得秘密图像的任何信息, 图(f) 为共享份1 和共享份2“或” 运算得到的图像, 同样无法从中识读出任何信息, 验证了安全性条件. 图(g) 为三幅共享份进行“或” 运算得到的解密图像, 叠加图像轮廓显现, 满足了对比性条件. 相较于图(b), 图(g) 轮廓信息还原较为完整. 作为黑色像素块分享的秘密像素块可实现完全恢复, 而白色像素块只有1/4 为白色, 观察可见, 白色区域出现明显的颗粒感. 图2 (3,3) 门限结构下分享结果Figure 2 Encryption results on (3,3) threshold scheme 通过对比参考文献, 结合共享份填充方式、平均对比度、方差、细线问题和计算复杂度, 分析各方案的优劣. 秘密图像尺寸为256×256 像素的二值图像, 存取结构为(3,3) 门限结构, 分享条件设置同上一节. 图3 和图4 分别展示了不同方案对“龙” 图和细线图的恢复效果图, 由实验结果观察可知, Yang 方案由于采用了基矩阵单列分享的方式, 反映在恢复图像中, 视觉效果表现为黑白像素分布不均匀、低频噪声集中、颗粒感较强, 以致图4(c) 中, 黑色线条掩盖被完全掩盖. Hou 等人和Liu 等人均采用定长m分享,由于改进了基矩阵选择条件, 后者显示质量较前者有所提升, 但改进效果不明显. 图3 “龙” 图实验结果对比Figure 3 Recovery results of competitive schemes on “dragon” image 图4 细线图实验结果对比Figure 4 Recovery results of competitive schemes on “thin-line” image 相较于对比方案, 本方案秘密图像白色区域相应于恢复图像的位置, 黑白像素分布均匀, 无明显少数像素集聚, 平滑度优于对比方案. 对于秘密图像中的细节, 如龙须等部分, 对比方案的恢复结果均有明显的断续甚至消失, 本方案恢复结果较为连续, 处理细节的能力有所提升. 图4 展示了各方案细线处理结果, 本方案恢复图像的黑色线条比较清晰完整地恢复出来, 对横线、竖线和斜线的处理效果都较佳, 细线效果整体上优于对比方案. 参数对比如表1 所示. 表1 (3,3) 存取结构下各方案对比结果Table 1 Comparative results on (3,3) threshold (1) 块方差. 块方差表征秘密像素块映射到恢复图像中块灰度值的波动程度, 方差越小, 则图像整体视觉感官越好. 令m代表基矩阵的列长,b代表列长为m的秘密像素块中黑色像素数量,h代表黑色像素恢复后的灰度,l代表白色像素恢复后的灰度. Yang 方案、Zhang 等人方案、Hou 等人和Liu 等人方案的方差分别表示为: 本方案中, 单位块尺寸x×y=m, 则灰度集合为ζ={0,1,2··· ,m}, 设满足上阈值条件的灰度集合为P={0,1,··· ,p}, 满足下阈值条件的灰度集合为Q={q,··· ,m}. 若秘密像素块满足上阈值和下阈值, 其方差为零; 若不满足, 则以p1= (g −|P|)/(|ζ|−|P|−|Q|) 的概率选择C0, 以p2=(|ζ|−g −|Q|)/(|ζ|−|P|−|Q|) 的概率选择C1, 方差可以表示为 (2) 细线问题. 细线用以评估方案处理细节信息的能力, Liu 等人定义了三类细线问题(TLP), TLP-1 指在白色背景下黑色细线消失问题, TLP-2 指黑色背景下垂直线条消失问题, TLP-3 指细线变粗问题.Yang 方案和Zhang 等人方案存在TLP-1 问题, Hou 等人方案和Liu 等人方案存在TLP-1 和TLP-3 问题, 本方案存在TLP-3 问题. 虽然本方案带来细线变粗的问题, 在相同条件下, 恢复效果较对比方案更优. (3) 计算复杂度. 设灰度秘密图像的行宽、列宽分别为M和N, 上述对比方案计算复杂度都是O(MN). 分享算法根据图像内容动态调整每次分享的秘密像素块尺寸, 如若考虑一般情况, 则复杂度计算较为困难, 因此考虑两种极端情况. 一是秘密图像全部按单位块分享, 则该方案蜕化为定长多像素概率型视觉密码, 根据已有知识, 定长多像素概率型视觉密码方案的计算复杂度是秘密图像尺寸的线性函数; 二是秘密图像按一个整体分享, 分享矩阵级联次数与秘密图像的尺寸成正相关线性关系, 可知计算复杂度亦是秘密图像尺寸的线性函数. 因此, 综合上述两种情况, 可知本方案的计算复杂为O(MN). 针对现有像素不扩展视觉密码方案恢复图像细节信息损失以及视觉质量较差的问题, 在分析图像的像素分布特征的基础上, 采取块尺寸由大到小调整、分类处理的方法, 区分秘密图像中低频和高频区域, 采取不同的分享方法, 通过调控高频区域中单位块灰度与分享矩阵的映射关系, 增强恢复图像中部分细节表现. 实验结果表明, 本方案恢复图像颗粒感较低, 秘密图像细节恢复较为完整, 线条连续, 细线图像测试结果表明, 本方案对不同走向的线条均有较好的恢复效果, 细线处理能力较对比方案有明显优势. 本方案基于(k,n) 门限存取结构, 同样适用于通用存取结构.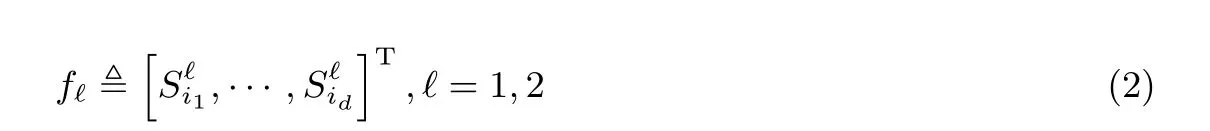
2.2 典型像素不扩展视觉密码方案


3 方案设计
3.1 分享原理

3.2 有效性证明

4 实验及结果分析
4.1 有效性验证


4.2 对比分析


4.3 参数对比
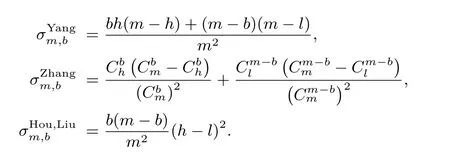

5 结论

