一类新的基于元胞自动机的S 盒的线性性质研究*

关 杰, 卢健伟, 刘 帅

战略支援部队信息工程大学, 郑州450001

1 引言

元胞自动机[1]是一种用来模拟和分析复杂离散问题的并行计算模型, 能够由一些简单的局部规则产生较为复杂的变换, 组合后可以实现混淆和扩散[2], 也可以用于伪随机数生成器的构造[3], 因此在密码学中有许多的应用. 我们可以将元胞自动机的变换过程定义为S 盒变换, 称其为基于元胞自动机的S 盒[4].这类S 盒一般实现代价较低, 并且有良好的安全性能, 最经典的是作为SHA-3[5]标准之一的Keccak 杂凑函数[6]的S 盒. 另外, Panama[7]、RadioGatún[8]、Subterranean[9]和3Way[10]所使用的S 盒也与Keccak 的S 盒有相同的局部规则.

文献[11] 中提出了一类新的基于元胞自动机的S 盒Fnnew, 它的局部规则的作用域范围为5 个元胞,具有较小的软件与硬件成本. 该类S 盒的具体描述如下:

2 基本概念

3 的线性性质分析

那么ρf(0)=0.

引理2[14]若布尔函数f(x) 和g(x) 是互为仿射等价的, 则ρf(0)=ρg(0).

该引理揭示了对于一个布尔函数的输入变量进行可逆线性变换后, 在0 点的Walsh 谱不变. 史丹萍等人给出了一个不相交化算法(算法1[14], 具体见附录), 可以有效地将任意给定的二次布尔函数转换为不相交二次型.

引理3[14]对于不相交二次型f=xi1xi2+···+xi2k−1xi2k+xj1+···+xjs,f在0 点的Walsh谱值计算方法如下:

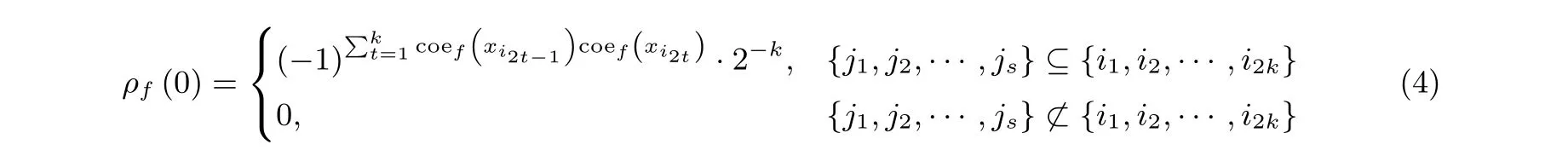
这里coef(xu) 表示xu在f中的系数.

引理3 提供了计算不相交二次型在0 点的Walsh 谱值的一种方法, 其中k表示f中不同二次项的个数, 根据算法1 和引理3 我们可以有效地计算出任意二次布尔函数在0 点的Walsh 谱值.

3.1 关于Fnnew 谱值取值范围的猜想证明

文献[12] 给出了针对Keccak 算法S 盒的相关结论的证明, 然而Keccak 算法S 盒的局部规则只有一个二次项, 因此从Walsh 谱的定义入手, 分析η·X ⊕µ·Y的结构即可证明. 然而Fnnew的局部规则中有两个二次项, 且二次项之间有一个公共变量, 所以从Walsh 谱的定义入手直接证明猜想1 是十分困难的.

本文从f∗η,µ的结构入手, 首先将f∗η,µ经过算法1 后化成的不相交二次型记为ˆf, 由于f∗η,µ与ˆf是互为仿射等价的, 由引理2 可知两者在0 点的Walsh 谱值相等, 再由引理3, 分析猜想1 中k的取值等价于分析ˆf中不相交二次项的个数. 下面给出定理1 及其具体证明.

当n为偶数时:

(2) 假设n=t ≥6 且t为偶数时, 结论成立, 下证n=t+2 时, 结论也成立.

3.2 Fnnew 的掩码结构和计数

下面考虑掩码对计数问题, 由上述证明过程可知, 一个输出掩码µ对应四个输入掩码η, 故当n ≥5且w(µ)=1 时掩码对数为4n,而当n=6 时还存在w(µ)=6 的情况,对应的掩码对数再加4,得证.

(1)w(µ)=2,µi0=µi0+1=1,ηi0+4=1;

(2)w(µ)=2,µi0=µi0+2=1,ηi0+3⊕ηi0+4=1;

(3)w(µ)=3,µi0=µi0+1=µi0+2=1,ηi0⊕ηi0+3=1;

(4)w(µ)=3,µi0=µi0+1=µi0+3=1,ηi0⊕ηi0+1⊕ηi0+2=1;

(5)w(µ)=4,µi0=µi0+1=µi0+2=µi0+3=1,ηi0+2⊕ηi0+3⊕ηi0+4=1;

(6)w(µ)=5,w(η) 为奇数;

且此时满足|ρFn(η →µ)|=1/4 的掩码对数为416.

证明: 由引理2 和引理3 可知, 非平凡相关优势取到最小值1/4 当且仅当f∗η,µ经过算法1 后得到的式子ˆf中有两个不相交的二次项, 即不存在独立的单次项, 由算法1 可知当w(µ)=1 时显然ˆf中只有一个二次项, 此时相关优势不可能取到1/4. 下面讨论w(µ)̸=1:

4 结束语

基于元胞自动机的S 盒已经被应用于许多密码算法中, 但结构上都与Keccak 类S 盒类似. 文献[11]中提出了一类新的基于元胞自动机的S 盒, 并分析了其置换与差分性质, 指出该类S 盒有着比Keccak 类S 盒更好的差分性质. 本文进一步研究了其线性性质, 将相关优势取值问题转化为不相交二次型中二次项的个数问题, 有效地解决了这类S 盒的Walsh 谱分布规律问题. 研究表明, 这类S 盒的线性性质也优于Keccak 类S 盒. 接下来的工作是分析这类S 盒的其它密码学性质, 为评估其替代Keccak 类S 盒后算法的安全性提供技术支持.

附录

表1 相关优势计数表[11]Table 1 Count of related advantages table [11]