麻雀搜索算法在物流配送中心选址的应用

阮信波 刘丽华 陈丽瑾

[摘要]介绍了求解选址问题的麻雀搜索算法，并将该算法应用于物流配送中心选址问题的求解，最后进行了一个案例分析，在实例中与粒子群算法进行对比，通过使用麻雀搜索证明该算法的有效性。

[关键词]物流配送中心;选址;麻雀搜索算法

[中图分类号]F224.0;F252.14[文献标识码]A[文章编号]1005-152X（2021）12-0040-04

Application of Sparrow Search Algorithm in Location Selection of Logistics Distribution Center

RUAN Xinbo，LIU Lihua，CHEN Lijin

（School of Science，Guangxi University ofScience& Technology，Liuzhou 545006，China）

Abstract：In this paper，we introduced the sparrow search algorithm for solving the location problem，then applied it to the location problem of a logistics distribution center，and finally，through a case analysis，compared it with the particle swarm algorithm，which proves the effectiveness of the algorithm.

Keywords：logistics distribution center;location selection;sparrow search algorithm

0引言

已经有很多学者就物流中心选址问题提出了很多办法。如杨茂盛，等[1]采用重心法解决了离散模型的配送研究，刘海燕，等[2]提出了物流配送中心选址模型，杜颖[3]提出了基于聚类分析解决物流中心选址的问题，黄敏镁[4]使用粒子群算法求解物流选址中心模型，王振中[5]研究了层次分析法在物流选址中心问题的应用，武明帅，等[6]提出了使用布谷鸟算法解决以配送中心总成本最低为目标函数的混合整数规划模型的办法，程赐胜，等[7]提出了离散粒子群算法求解城市物流节点选址模型，并证明该算法的有效性。

使用科学合理的方法建立一个物流配送中心可以有效地降低配送成本，并且在此基础上提高物流配送的效率，同时还能提高客户的满意度，从而能够间接地增加物流公司的收益。本文将使用麻雀搜索算法解决物流选址中心问题，并与粒子群算法（本文均称为PSO算法）在实例中作对比加以验证该算法的有效性。

1求解选址问题的麻雀搜索算法

麻雀搜索算法[8]（Sparrow Search Algorithm，SSA）是在2020年提出的，该算法是受麻雀觅食与反捕食行为而启发的群体智能优化算法。在SSA中，每个优化问题的解类似于搜索空间中的一只麻雀，每只麻雀都有各自的能量，每只麻雀的能量值使用函数适应值来表示。其中麻雀分为发现者与参与者，发现者的适应值通常大于参与者的适应值，主要规则如下：

（1）有些麻雀作为发现者，在整个麻雀种群中具有较高的能量，它们主要负责搜寻资源充足的区域并且所有作为参与者的麻雀都是以发现者的位置来探查到最好的觅食区域。

（2）当发现者发现捕食者时，它会向整个麻雀种群发送警报信号，当预警信号的值大于安全阈值时，作为发现者的麻雀会引导作为参与者的麻雀到其他安全区域觅食，而没有收到预警信号的麻雀则会自由移動寻找食物资源以补充能量。

（3）每只麻雀都能在发现者和参与者之间随意切换，但两者的比例在种群中是固定的。

（4）麻雀觅食时，作为参与者的麻雀总是可以通过争夺发现者的食物资源，在发现者周围的区域寻到最丰富的资源和饲料。

1.1模型假设

（1）待定物流配送中心的库存总能满足需求点的需求。

（2）不考虑从工厂到待定物流配送中心的运输成本。

（3）不考虑选定区域内待确定配送中心的建设成本。

（4）不考虑交货时间、天气和车辆情况。

1.2符号假设

（1）U表示总运输成本。

（2）用（x，y）表示待确定物流配送中心的横坐标和纵坐标。

（3）w_i表示产品从配送中心到需求点i的单位运费率。

（4）c_i表示产品从配送中心到需求点i的出货量。

（5）d_i表示待定配送中心与需求点i之间的欧式距离。

1.3建立模型

设有n个需求点和一个物流配送中心，物流配送中心到每个需求点需要一定的货物量以及一定的配送费用，以待定物流配送中心到所有需求点的总体配送费用最少为目标函数建立模型如下：

d_i使用欧几里得距离公式计算，即：

其中，x，y分别为待定物流配送中心的横纵坐标，x_i，y_i别为需求点i的横纵坐标。

1.4将麻雀搜索算法应用于物流配送中心选

址问题的求解

在SSA算法中，建立虚拟麻雀来寻找食物，所有麻雀的位置X可以通过以下方式来表达：

其中，m为麻雀的个数，X_j=（x_j，y_j）（j= 1，…，m）即待定最优的物流配送中心的第j个可行解。

所有麻雀的适应值F_x可以表示为：

发现者的位置更新方式如下：

参与者的位置更新公式如下：

在模拟实验中，随机生成麻雀在种群中的初始位置，假设10%至20%的麻雀会意识到危险，则收到危险信号的麻雀更新它的位置如下：

1.5算法的主要步骤

步骤1初始化基本参数：麻雀搜索算法的最大迭代次数G，麻雀总数M，麻雀的发现者数量PD，麻雀的参与者数量M-PD，感知危险的麻雀数量SD，麻雀感知到危险信号的参数R₂。

步骤2分配发现者与参与者的数量，获取当前最优麻雀位置和全局最优的麻雀位置，并随机设置警戒者位置。

步骤3计算每只麻雀在当前位置的适应值，并寻出最好的个体与最坏的个体及当前适应值最优的麻雀位置与全局最优的麻雀位置。

步骤4根据式（1）—式（3）分别更新发现者与参与者的位置并更新警戒者的位置。

步骤5更新最优适应值的麻雀位置。

步骤6判断是否结束，若结束则算法结束，否则转步骤2。

2实例分析

问题分析：某公司要在某地区建立一个物流中心，要求各个需求到物流中心的运输成本最小，现有需求点的数据见表1。

表1中，S_i表示10个物流需求点的名称，每个需求点的位置使用（x_i，y_i）来表示，物流中心到各个需求点的运价与需求量分别为w_i与c_i，其中i=1，…，10。

采用麻雀搜索算法求解该实例，并且与粒子群算法做对比。其中麻雀搜索算法的每只麻雀，粒子群算法的每一个粒子都称为一个可行解，任一可行解依据位置更新公式式（1），式（2），式（3），更新一次其横纵坐标称为可行解的一次算法迭代次数，可行解个体在算法开始到结束的过程中，依据位置更新公式发生横纵坐标变换次数的总和称为一个可行解的算法迭代总数。麻雀搜索算法的参数设置：最大迭代次数G=1000，麻雀总数M= 100，麻雀的发现者数量PD = 20，感知危险的麻雀数量SD = 20，麻雀感知到危险信号的参数R₂=0.8。

运行程序得到如图1-图4所示结果。

图1表示可行解个体与需求点在地图上的分布位置，其中x轴与y轴分别对应需求点与可行解的横纵坐标，五角星表示可行解个体，圆圈表示需求点。

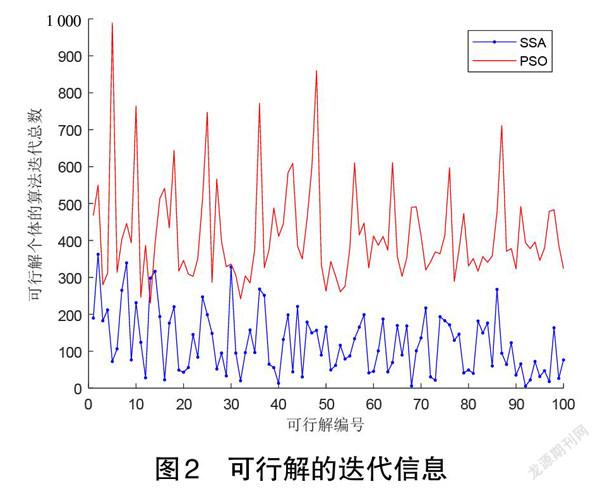
图2表示从算法开始至结束各个可行解的算法迭代总数曲线。从中能够看出可行解的算法迭代总数情况。SSA算法的可行解相较于PSO算法的可行解具有更少的变化，出现这样情况的原因是SSA算法中拥有10%至20%的可行解（作為发现者的麻雀），整体的麻雀都会参照这10%至20%的可行解来更新（或称为迭代）他们的位置，其中横坐标轴表示编号由1至100的可行解，纵坐标轴表示每一个可行解的算法迭代总数。

图3表示可行解随着算法迭代次数的变化而不断向最优解趋近。从图中可以看出，SSA算法与PSO算法的收敛曲线是十分相近的，由于PSO算法在搜索最优解时有可能陷入局部最优解的情况，因此SSA算法在此基础上作了一些优化，其可行解会尝试跳出当前已经找到的最优解情况并继续寻找更好的解。SSA算法在迭代过程中如果确定了当前的可行解就是全局最优解时，其所有可行解都将收敛于最优的适应值。其中横坐标轴表示所有可行解在第0-1 000轮算法结束时，可行解个体的平均迭代次数。纵坐标轴表示SSA与PSO算法的适应值（物流成本），适应值即为算法评估每个可行解在地图上的好坏情况，可行解个体的适应值越小，说明该可行解个体就越好，否则就越差。

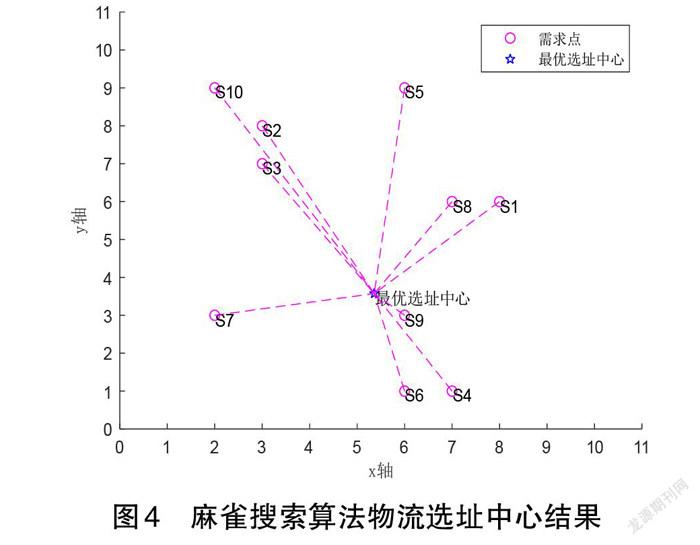
图4表示本文算法结束时得到各个需求点与最优选址中心之间都有最小的适应值，即每个需求点到达最优选址中心都有最小的物流成本，因此得到各个需求的适应值之和到达最优选址中心也有总体最小的物流成本，其中横坐标轴与纵坐标轴分别对应需求点与可行解的横纵坐标。

3结果分析

运用PSO与SSA算法求解此实例的最终结果都为（x，y）=（5.36，3.57），求解得到的最优适应值为55 291.68元，即说明该物流配送中心选址位置坐标为（5.36，3.57），求得总体物流成本费用最少。结果证实了麻雀搜索算法在解决物流配送中心选址问题是可行的，并且具有一定的扩展性。采用麻雀搜索算法求解问题时只需要修改相关的参数即可运用于不同的物流配送中心选址模型。

[参考文献]

[1]杨茂盛，姜华.基于重心法与离散模型的配送中心选址研究[J].铁道运输与经济，2007（7）：68-70.

[2]刘海燕，李宗平，叶怀珍.物流配送中心选址模型[J].西南交通大学学报，2000（3）：311-314.

[3]杜颖.基于聚类分析的江西省物流中心选址问题[J].中外企业家，2019（36）：227-228.

[4]黄敏镁.粒子群算法在物流中心选址中的应用[J].计算机工程与应用，2011，47（4）：212-214.

[5]王振中.层次分析法在配送中心选址中的研究与应用[J].物流工程与管理，2010，32（1）：97-100.

[6]武明帅，王巍，孙理越.基于布谷鸟搜索算法的物流配送中心选址[J].经济师，2021（2）：252-253，255.

[7]程赐胜，蒲云虎，高慧.基于离散粒子群算法的城市物流节点选址模型[J].长沙理工大学学报（自然科学版），2008（2）：20-24.

[8]薛建凯.一种新型的群智能优化技术的研究与应用[D].上海：东华大学，2020.