铁路曲线地段钢轨生存寿命评估与分析
何庆,杨康华,杨翠平,高天赐,王启航,王平,刘勇
(1. 西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都610031;2. 四川大学 商学院,四川 成都610065;3. 中国铁路成都局集团有限公司,四川 成都610082)
铁路运输在我国的应用十分广泛,具有运量大、耗能低、安全舒适等特点。为满足经济发展的需求,铁路的运行速度、轴重、行车密度逐年增加,钢轨状态劣化加快并且钢轨伤损类型也朝多元化发展,严重威胁列车的行车安全。其中,山区铁路的设计标准低且曲线半径小,列车通过时会产生较大的横向轮轨力和垂向力,在二者共同作用下会加剧轨道状态劣化,使得山区铁路的钢轨伤损情况格外严重。开展钢轨劣化规律研究,根据钢轨状态制定合理的维修计划,并兼顾铁路系统的风险控制和经济效益,是铁路工务管理部门亟需解决的问题之一。当前,对钢轨使用寿命的评估模型主要是基于病害发展的物理分析模型和基于失效统计的数据分析模型。ZAREMBSKI等[1−2]为了预测轨道设备的退化状况,建立完整的轨道退化模型(Integrated Track Degradation Mod‐el),其中重点分析了轨道几何缺陷对钢轨伤损发展的影响。刘亮等[3]根据断裂力学理论,算出钢轨设备上的动态加载弯曲应力、温度应力以及残余应力,利用钢轨疲劳裂纹扩展速率评估其剩余寿命,再进一步分析钢轨材料、列车速度系数等对其寿命产生的影响。VESKOVIC 等[4]使用模糊逻辑方法对影响铁路中断因素的非线性相互作用进行建模,该模型考虑了气候因素。利用有限的数据,结合钢轨断裂时的温度来预测钢轨的断裂,预测结果与实际断裂情况相近。白磊[5]在考虑钢轨劣化状态的异质性等劣化特性的基础上,结合钢轨网格化管理理论,基于马尔科夫随机过程分析理论,针对不同网格单元构建使用寿命预测模型。GHO‐FRANI等[6]利用贝叶斯生存分析方法,分析了轨道几何缺陷、列车通过总重、区段道岔数量等风险因素对钢轨伤损出现概率的影响,并绘制了钢轨的生存函数曲线。GHOFRANI等[7]假设区段钢轨伤损出现频次满足Poisson 先验分布(参数考虑列车通过速度、轨道几何缺陷、道床捣固等因素),结合钢轨伤损的物理模型,利用近似贝叶斯计算框架(ABC)预测钢轨伤损出现频次的后验分布,该方法在常规“数据”分析模型的基础上,将钢轨伤损出现频次的预测精度提升了20%。安茹等[8]将连续的轨道划分成多个长度为200 m 的网格单元,利用cox比例风险模型,对不同网格单元内多个风险因素对钢轨折断事件发生的影响程度进行量化分析。现有的预测钢轨使用寿命研究工作存在以下不足:1) 钢轨伤损形式具有随机性和多样性,这些模型不能量化各风险因素对钢轨劣化速率的影响,难以准确评估不同服役条件下钢轨使用寿命。2) 多数文献针对较长、连续线路区间的钢轨设备建立了统一的寿命评估模型,基于病害机理分析的评价模型未考虑钢轨服役的环境不同,无法实现不同环境中钢轨使用寿命的个性化评估。
1 曲线段钢轨生存寿命分析模型
1.1 钢轨网格非均匀划分
钢轨服役环境对钢轨病害发展有很大的影响,不同环境下的风险因素对钢轨劣化影响存在差异。山区铁路所处地理环境恶劣且沿线的环境复杂多变,风险因素可能在较短区间内发生巨大变化,这导致该区间内钢轨的劣化过程不相同,如果直接用等长网格划分钢轨(如图1(a)),可能将不同半径的曲线或将不同坡度划分到同一网格内,造成同一网格内的曲线半径和坡度存在较大差异,使得钢轨寿命评估出现较大的误差,尤其是小半径曲线段钢轨,因为不同曲线半径下的钢轨寿命差异较大。为了研究各风险因素对小曲线半径段钢轨生存概率的影响,本文采用非均匀网格划分方法对钢轨进行划分(如图1(b)),根据轨道实际线形数据将整条线路划分为若干个钢轨网格,各网格单元的长度并不相同,但需确保每个钢轨网格内的风险因素相同或是差异不大,选取其中信息完整的网格单元进行生存分析,实现风险因素的量化分析和钢轨使用寿命的预测。这样可以避免同一网格内的某种风险因素存在多个取值的现象,将从数据处理上提高模型的评估精度。
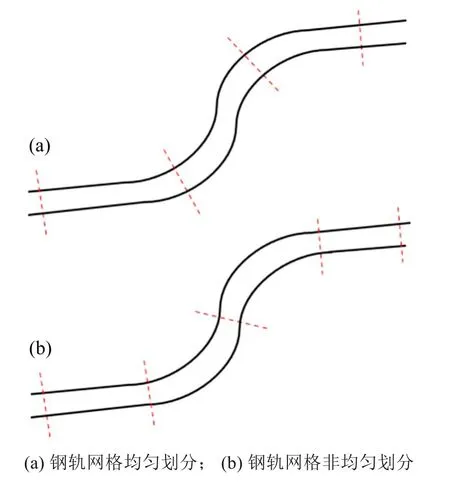
图1 钢轨网格划分Fig.1 Rail division
1.2 生存分析模型构建
1.2.1 生存分析模型
钢轨从上道服役到换轨会经历多个状态阶段,且每个阶段的劣化速度和持续时间都不相同。因为这种不确定性特征导致钢轨状态何时开始转变、以何种路径转变以及转变速度都不确定[9](如图2)。

图2 钢轨劣化的不确定性Fig.2 Uncertainty of rail deterioration
钢轨的累计通过总重是一个非负变量,同时钢轨伤损劣化过程有不确定性,为解释钢轨重伤换轨与累计通过总重之间的关系,需要建立一个统计模型用于实证研究。因此,本文采用可靠度理论中的生存分析模型[10]来对钢轨重伤失效寿命进行评估分析。生存分析参数模型调整了不同网格区段之间的异质性,本文采用钢轨伤损数据相关的协变量来解释钢轨出现伤损时的累计通过总重,即钢轨生存寿命,并且可以量化具体的线形变化对钢轨生存寿命的影响,其数学模型可描述为:
假设T为钢轨出现重伤时该处钢轨的累计通过总重,模型包括以下函数:
1) 生存函数:表示钢轨出现重伤发生时的总运量T超过某一运量t的概率。

2) 失效函数:表示钢轨出现重伤发生时的总运量T未超过运量t的概率。

3)失效密度函数:表示钢轨在运量为t时瞬间出现重伤的概率,为F(t)的导数。
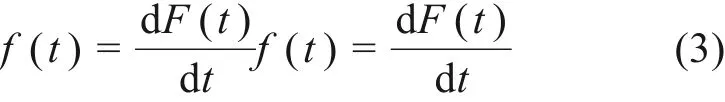
4)风险函数:表示当运量为t时,钢轨未出现重伤,但在下一时刻重伤出现的概率。

5) 累积风险函数:表示当运量到达t时为止,钢轨出现重伤发生的概率。

6) 基于钢轨的历史状态检测数据,记录钢轨从上道服役至出现重伤过程中故障率随通过总重的变化信息,可建立钢轨重伤失效风险函数,进一步来估计轨道段的生存或失效概率。

本文定义的生存分析中,关注事件为钢轨出现重伤,生存时间为钢轨从上道服役开始至出现重伤期间对应的累计通过总重。
1.2.2 加速失效模型
加速失效时间模型主要研究各类风险因素对生存概率的影响。各类风险因素对钢轨伤损发展的影响不同,具体表现在不同曲线半径、位置、坡度处的钢轨劣化速度、维护周期不同。各类风险因素可能会加快或减缓钢轨的劣化速度,从而影响生存吨数T。例如,轨道段中存在的缺陷会加快失效率,而维护工作会降低失效率。用S0和h0分别表示一般情况下钢轨生存函数和风险函数,但函数形式是不确定的。AFT 模型中的生存和失效函数分别定义为:

其中:X是协变量即风险因素的集合,而β是这些协变量系数的向量值。
协变量对生存函数存在可乘作用,AFT 模型假设协变量与生存时间(累计通过总重T)存在对数线性关系如(9)所示。其中w为误差项,因此协变量与生存时间的对数也存在线性关系。
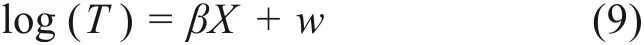
1.2.3 风险函数分布
利用风险函数求解参数化的ATF 模型,可以定量分析各类风险因素的影响程度。为找到最符合钢轨病害分布规律的风险分布函数,本文考虑了不同分布的风险函数,分别为Weibull 分布、Log-Normal 分布、Log-Logistic 分布。为引入风险因素,将位置参数假设如为:

式中:xi为造成钢轨重伤失效的第i个风险因素的取值,可以表示为网格区段的曲线半径、轨道几个形位缺陷个数与钢轨重伤失效相关的参数;βi为异质性系数;α为截距。
1.2.4 模型参数估计
本文采用的参数估计方法为极大似然估计(maximum likelihood estimation,MLE),该方法具有直观、易懂、灵活等优点,是一种十分成熟的参数估计方法[11]。根据各网格内钢轨服役过程中的状态和风险因素数据,利用MLE 方法估计协变量参数βi的值。最符合钢轨病害分布规律风险函数可利用赤池信息量准则(Akaike information criterion,AIC)进行选择[12],AIC 是衡量统计模型拟合优良性的一种标准,该指标是在熵的基础上建立的,它可以用来评判所利用的模型的复杂度,以及模型拟合样本数据的适用性及优良性[13]。

式中:k为带估计参数的数量,̂为模型的极大似然估计值。当2个模型之间存在较大差异时,差异主要体现在似然函数项,一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC 变小,但是k过大时,似然函数增速减缓,导致AIC 增大,模型过于复杂容易造成过拟合现象;当似然函数差异不显著时,上式第1项,即模型复杂度(k)则起作用,从而参数个数少的模型是较好的选择。选取AIC 最小的模型,不仅提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
2 钢轨实际数据的生存分析
2.1 数据来源及处理
本文的分析数据来自成都局2009 年—2019 年钢轨伤损记录表,铁路工务部门会对钢轨磨耗、剥离掉块、擦伤等钢轨病害的严重程度按等级划分,共有4个等级:轻伤、有劣化趋势的轻伤、重伤、折断。其中重伤和折断的钢轨需要立即更换。首先对重伤和折断钢轨进行初步的统计分析,不同范围曲线半径、内外轨上出现重伤和折断的比率(图3)。由图3(a)可知钢轨重伤和断轨主要出现在小半径曲线段;由图3(b)可知钢轨重伤和断轨大部分发生在曲线段的外侧。
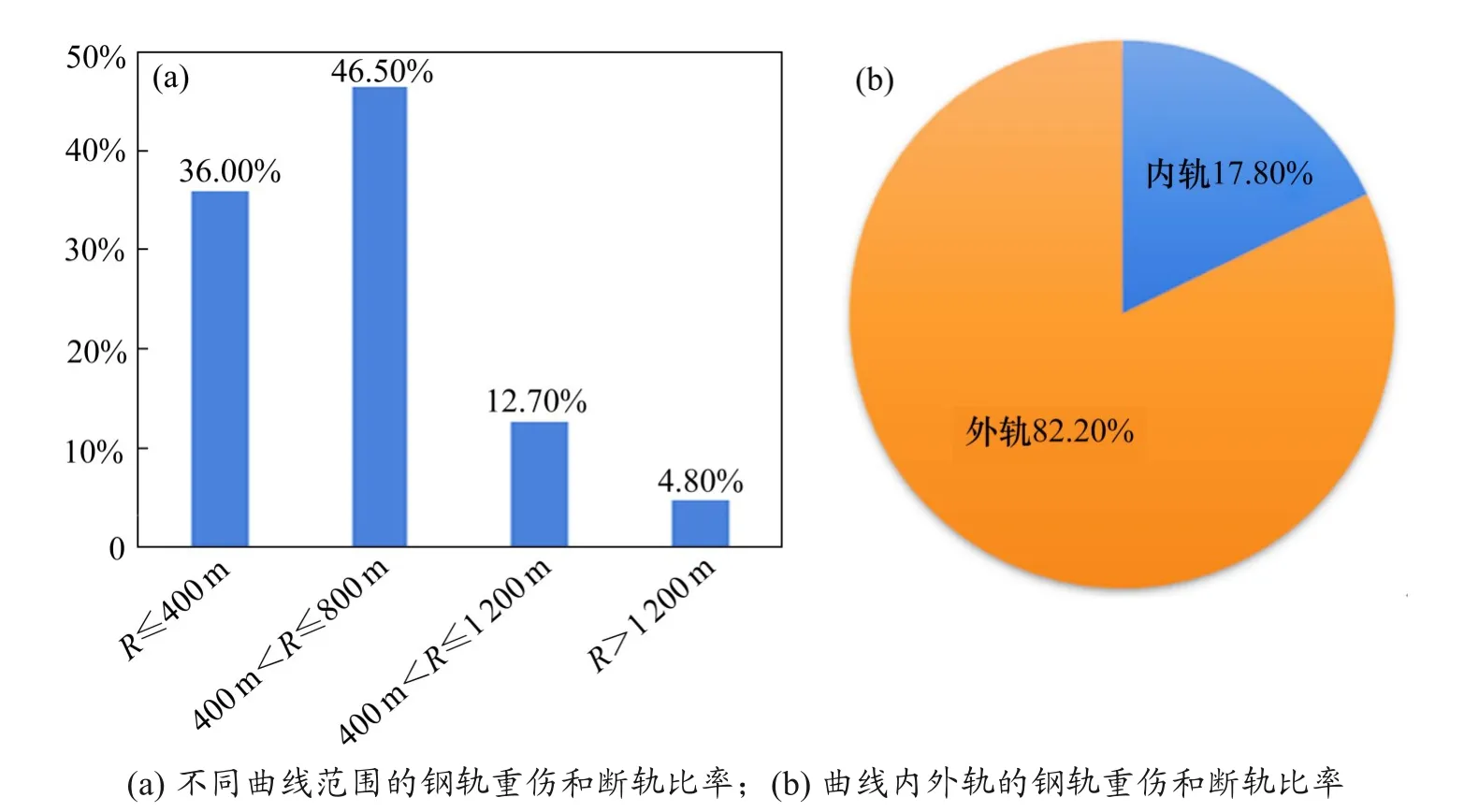
图3 钢轨伤损统计分析Fig.3 Statistical analysis of rail defect
因成昆、成渝、宝成线小曲线半径较多,本文对这3 条线路进行非均匀网格划分(表1),网格的长度各异,主要是确保在每个网格区段内的风险因素保持一致或变化不大,从而降低评估误差。最终共划分了1 434 个区段,包含重伤的区段279个。重伤主要包含轨头裂纹,约占43%;剥离掉块,约占22%;核伤,约占18%;其余类型的重伤占17%,如焊缝缺陷、夹渣等。
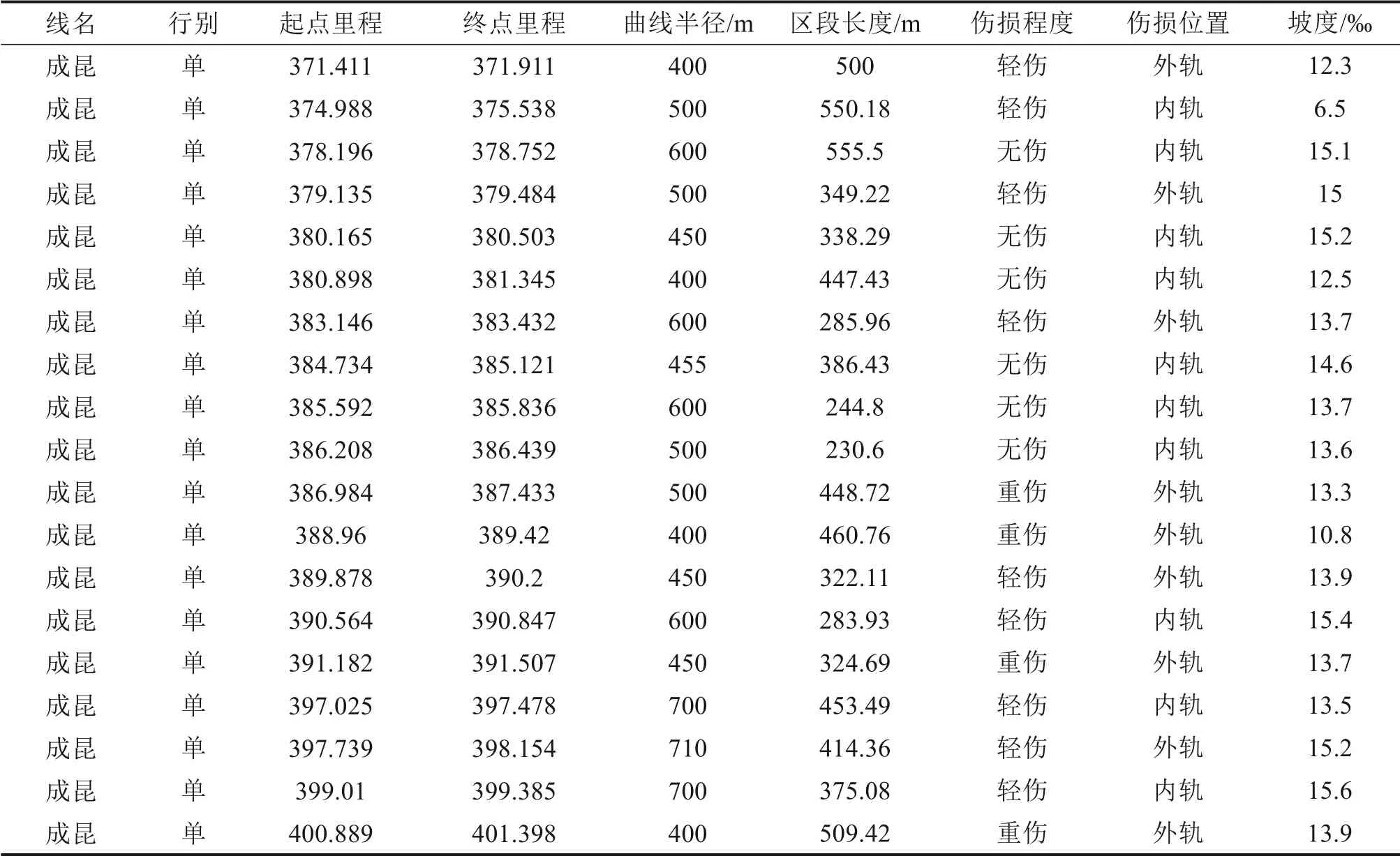
表1 非均匀网格划分表(部分)Table 1 Non-uniform grid division table
对于造成小半径曲线段钢轨伤损的风险因素,本文选取了曲线半径、伤损位置、网格区段长度、区段内最大坡度共4种风险因素,分析它们对钢轨发生重伤失效的影响程度,网格n内的风险因素表示为xn=[xn1,xn2,xn3,xn4],第i类风险因素对钢轨重伤失效的影响程度即为βi(i= 1,2,3,4),风险因素如表2所示。

表2 钢轨状态劣化影响因素Table 2 Influencing factors of rail state deterioration
2.2 钢轨生存寿命评估
2.2.1 模型参数估计结果
利用赤池信息量准则(AIC)选择最适合铁路生存数据分布的最优风险函数,3 种不同分布函数的对数似然值和AIC指标估计如表3。
由表3可知,对钢轨疲劳寿命数据进行生存分析时,Weibull 分布函数作为失效函数时模型的对数似然值和AIC 指标的绝对值最小,即针对本文所选用的数据,Weibull 分布函数最符合实际钢轨劣化规律,利用Weibull 风险函数所建生存分析模型求得的各风险因素参数结果如表4。

表3 疲劳伤损寿命预测模型估计结果Table 3 Estimation results of fatigue defect life prediction model

表4 钢轨疲劳伤损寿命风险因素参数估计结果1Table 4 Parameter estimation results of rail fatigue life risk factors 1
从表3中可以看出:风险因素最大坡度估计的回归系数对应的P大于0.05,说明在0.05显著水平假设下,最大坡度因素对钢轨出现重伤的影响不显著。其余3项影响因素的参数估计值在0.05显著水平假设下成立,说明这3项影响因素对钢轨出现重伤事件均有影响,去除最大坡度对钢轨出现重伤事件的影响,重新对模型进行参数估计,估计结果如表5。

表5 钢轨疲劳伤损寿命风险因素参数估计结果2Table 5 Rail fatigue life risk factor parameter estimation results 2
对参数进行重新估计后,曲线半径、伤损位置、曲线段长度这3个风险因素对钢轨疲劳伤损寿命均存在影响,形状参数值大于1,表示钢轨存在“老化”,随着时间的增加,故障率也会随着增加。该模型可以分析各风险因素对钢轨出现重伤事件的影响程度,其中参数估计值βi为正表示钢轨的寿命随着风险因素变量的增加而增加,参数估计值βi为负表示钢轨的寿命随着风险因素变量的增加而减少;估计值的指数值exp(βi)能够解释各风险因素对钢轨寿命的影响程度:
1) 钢轨寿命随着半径的增大而增大,由于列车通过半径越小的曲线钢轨时,轨道会受到更大的冲击力和离心力,轨道设备更容易出现严重伤损情况,文献[14]在对各类风险因素对钢轨折断事件影响的研究结论也印证了这一点。exp(βi)为1.000 5,表示曲线半径每增加100 m,因钢轨重伤换轨的钢轨累计通过总重增加5%,一般情况下曲线半径越大,钢轨的服役时间越长。
2) 伤损位置因素的回归系数βi为负,表示曲线段外轨的寿命比内轨的寿命短,这与图3(b)统计的外轨伤损多余内轨的情况相符。主要原因是当列出通过小半径曲线段时,曲线外股钢轨轨头受到较大的偏心压力,轨头内侧达到材料的屈服强度并出现疲劳裂纹,当裂纹劣化到一定程度轨头内侧可能出现剥离掉块的现象。exp(βi)为0.758,表示曲线段外轨的寿命是内轨的75.8%。
3) 划分区段时的区段长度对钢轨寿命也存在影响,回归系数βi为负,表示区段划得越长,区段内越容易出现钢轨重伤,且区段长每增加10 m,该区段的生存寿命会减少1%。这种推论是显而易见的,因为轨道的分段长度越大,该分段发生故障的可能性就越大。
2.2.2 钢轨寿命生存曲线
利用上述模型绘制了不同风险因素的影响下的生存曲线,其中baseline 是所有的钢轨生存期望拟合的生存曲线,未区分半径大小、内外轨位置、划分曲线长度,如图4。

图4 不同风险因素下的伤损生存曲线Fig.4 Defect survival curves under different risk factors
由生存曲线可知,在相同的列车累计通过总重下:1) 曲线半径越大,钢轨的生存概率越大;2)非均匀网格的长度越短,钢轨的生存概率越大;3) 处于曲线内侧的钢轨比曲线外侧钢轨的生存概率越大。根据铁路运营经验,铁路线路修理规则与管理部门制定养护计划时,都主要以不同半径等级为类别制定钢轨大修建议。由图3(a)可知,不同曲线半径下钢轨的生存曲线分布存在明显差异,从使用寿命差异性的角度体现了钢轨状态劣化的异质性,也说明了针对不同服役条件下钢轨进行寿命分析的必要性。
2.3 钢轨生存寿命对比分析
在钢轨生存分析中,不同半径生存曲线的期望值可作为该半径的钢轨生存寿命,一般情况下也可取生存概率为0.5 所对应的累积通过总重作为其生存寿命;铁路工务部门在运营现场也多使用累计通过总重来管理钢轨状态,在2019 版的《普速铁路线路修理规则》[15]中制定了曲线段钢轨大修阈值。本文将伤损生存寿命和修规换轨周期作对比分析,如表6。
由表6 可知,曲线半径R≤800 m 时,钢轨的生存分析评估寿命大于修规的大修阈值;800<R≤1 200 m 时,生存分析评估寿命在大修阈值范围内。产生这种情况的原因可能为:1) 修规中的更换周期为推荐阈值,在实际养护维修中,主要还是根据钢轨状态决定是否更换,养护状态较好钢轨的寿命可适当上浮30%~50%;2)钢轨探伤是需要伤损发展到一定大小时才能被探伤仪所发现,过小的伤损会出现漏报,这会增长服役时间,使得评估寿命增加;3) 影响钢轨寿命的因素除了钢轨伤损,还有钢轨的磨耗。曲线半径较小时的钢轨磨耗也较为严重,本文只将钢轨重伤作为换轨标准,实际存在未达到钢轨重伤但进行了换轨的情况。该情况未被考虑,使得评估寿命大于修规的换轨周期。

表6 小半径曲线段钢轨生存寿命对比分析Table 6 Comparative analysis of rail life in small radius curve section
3 结论
1) 钢轨的生存寿命随着半径的增加而增加。由于列车通过小半径曲线段的钢轨时,轨道会受到更大的冲击力和离心力,轨道设备更容易出现严重伤损情况。通过对不同曲线半径下的钢轨生存寿命分析,曲线半径每增加100 m,因重伤换轨的钢轨累计通过总重增加5%。
2) 曲线外轨的是生存寿命是内轨的生存寿命的75.8%。主要是因为当列车通过小半径曲线段时,曲线外轨轨头受到更大的偏心压力,使得轨头内侧更易达到材料的屈服强度并出现疲劳裂纹,当裂纹劣化到一定程度时,曲线外轨就可能出现剥离掉块等钢轨病害。
3) 划分的区段长度对钢轨寿命也存在影响,区段划得越长,区段内出现钢轨重伤的可能性越大。通过分析发现,区段长每增加10 m,该区段的生存寿命会减少1%。

